相机模型

相机与图像之间的关系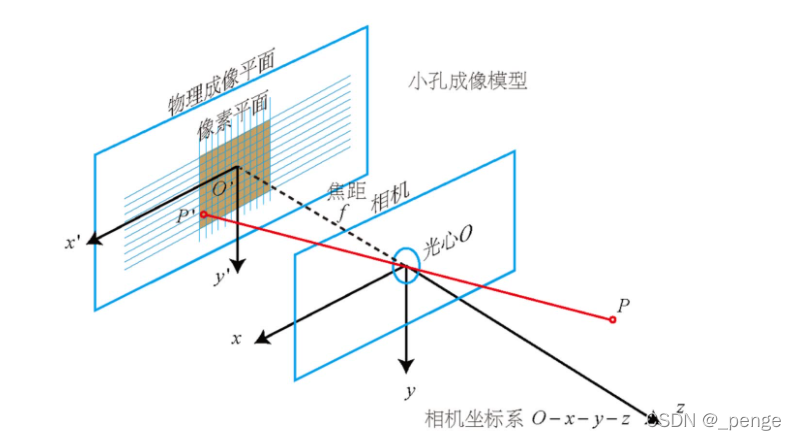

相机成像的大致流程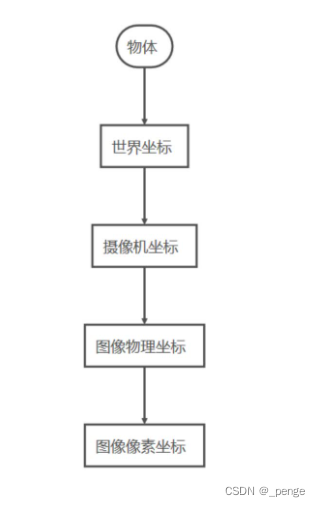

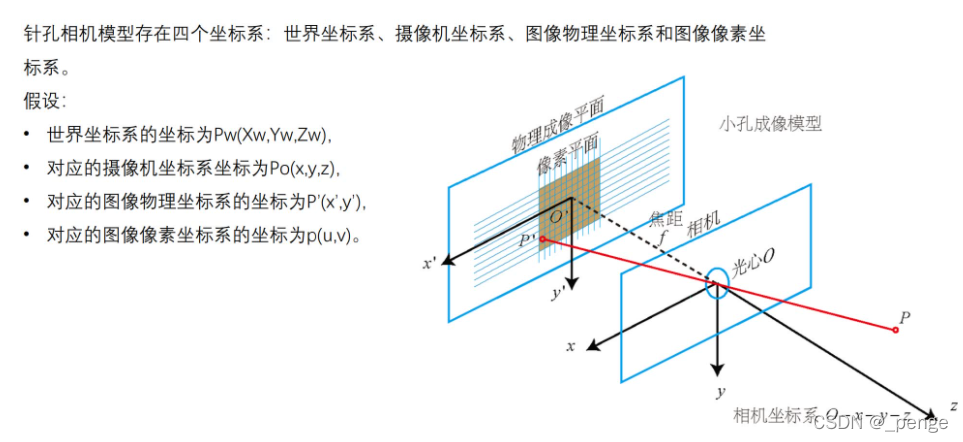
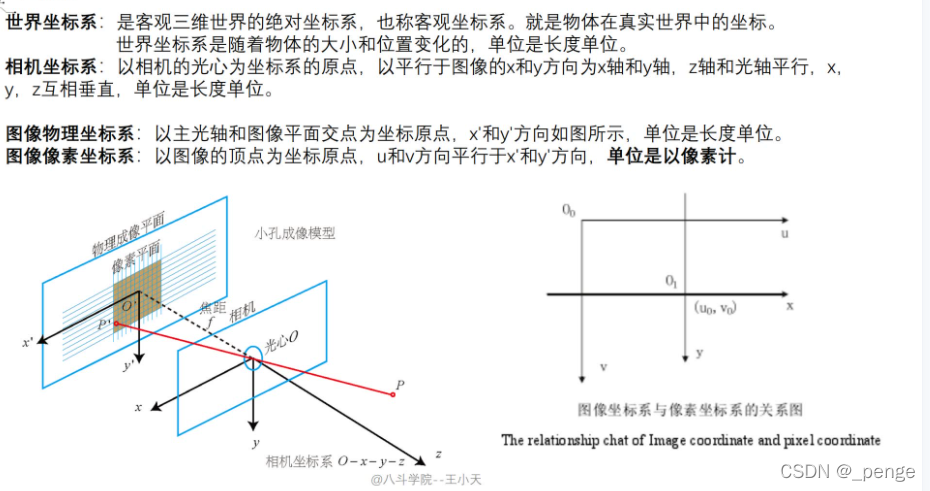
世界坐标系到摄像机坐标系

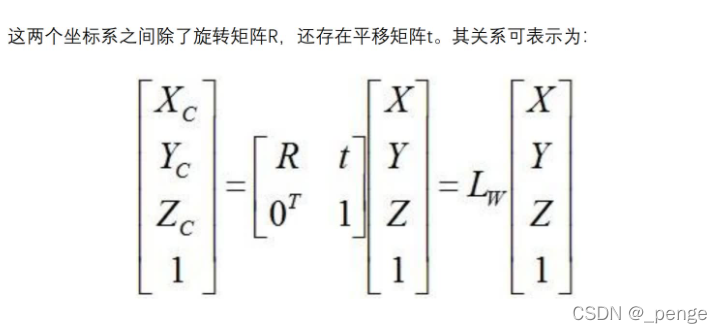
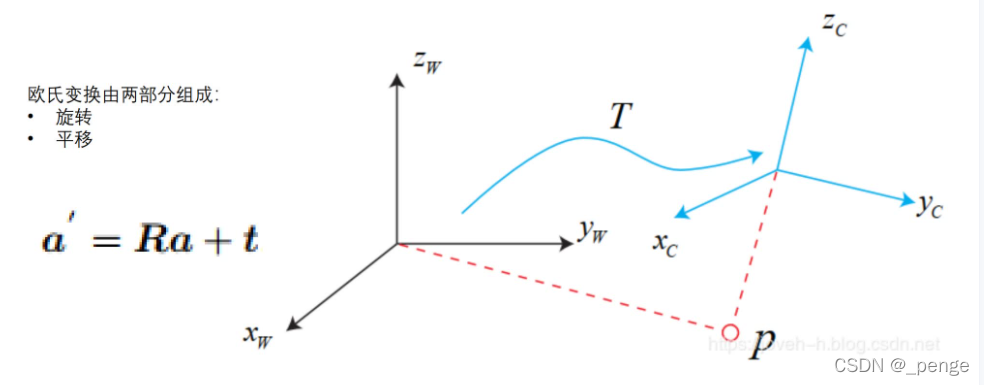
摄像机坐标系到图像物理坐标系

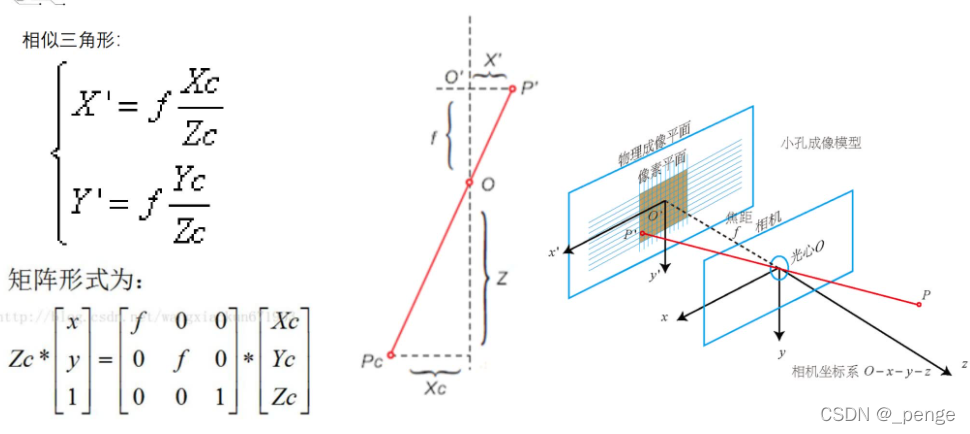
主要是根据相似三角形列出等式。

图像物理坐标系到图像像素坐标系

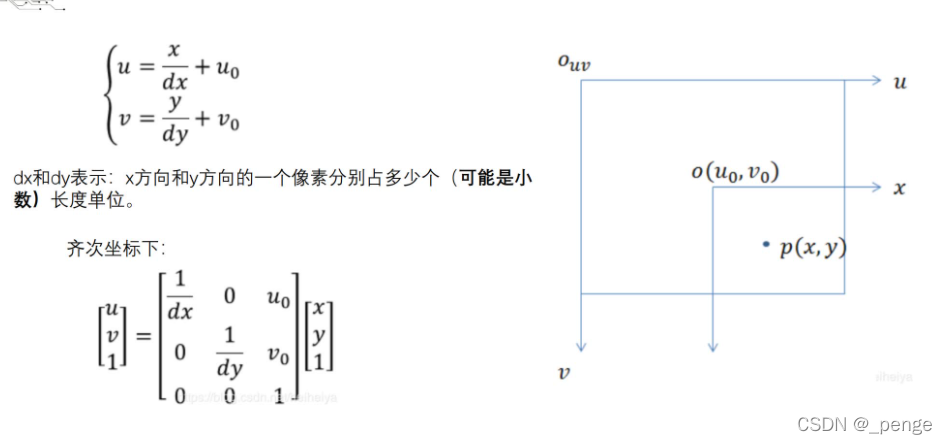
摄像机坐标系到图像像素坐标系

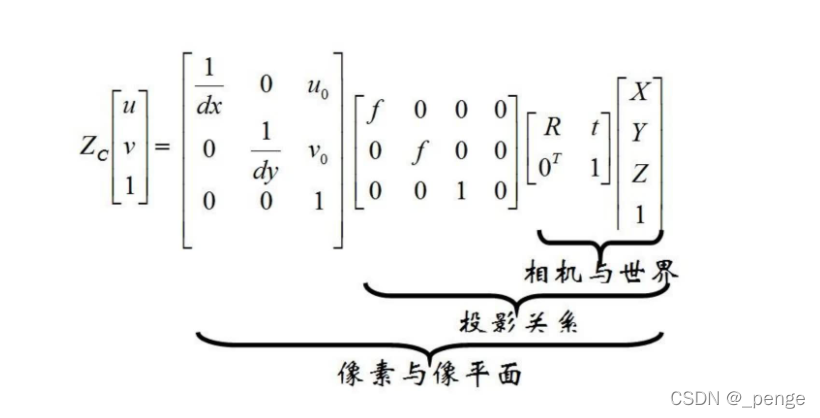
世界坐标系到图像像素坐标系

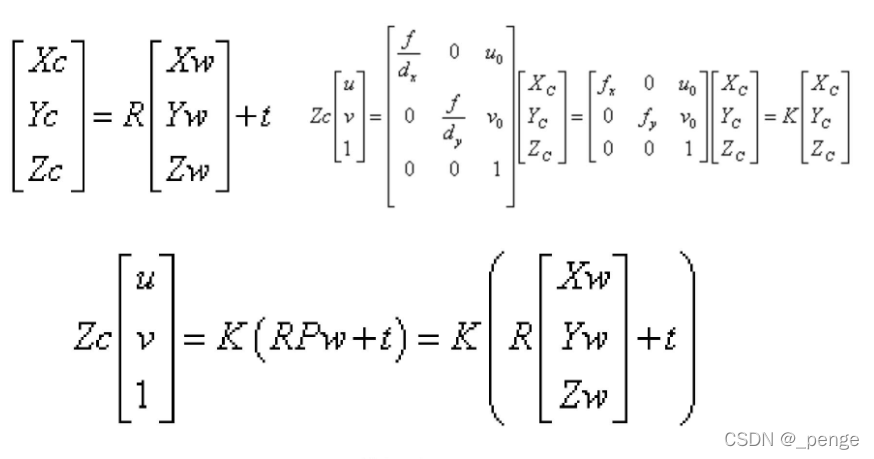
相机成像原理

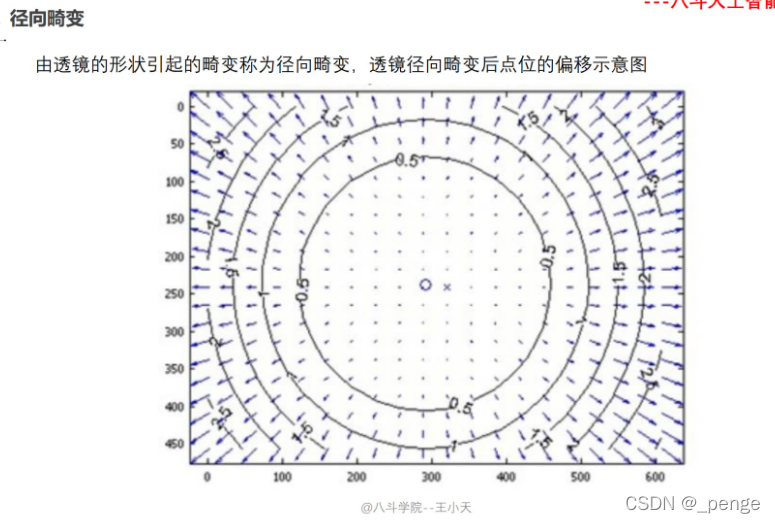
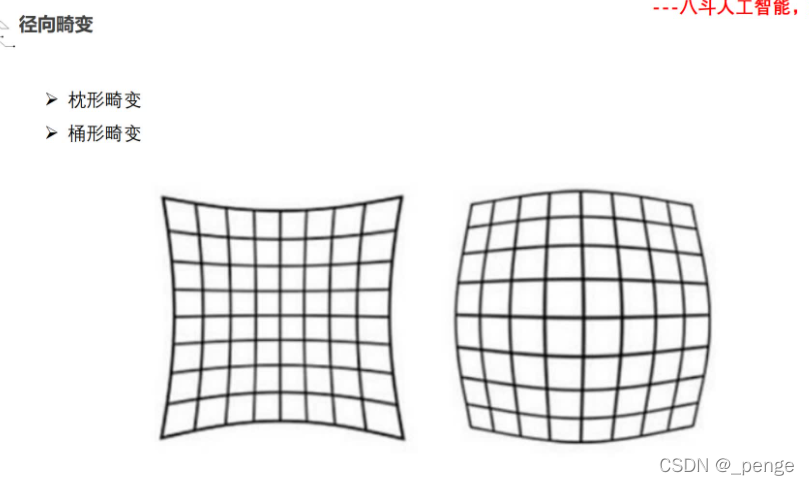
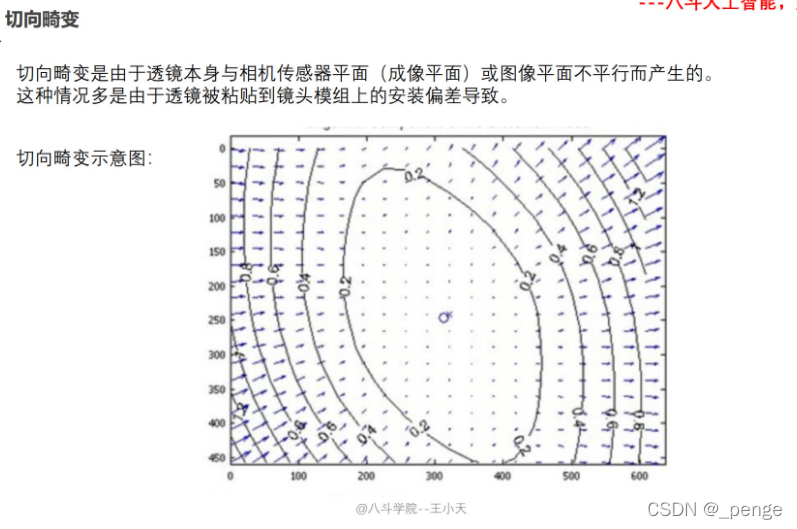
镜头畸变

（简单了解）

透视变换

定义

透视变换(Perspective Transformation)是将图片投影到一个新的视平面(Viewing Plane)，也称作投影映射(Projective Mapping)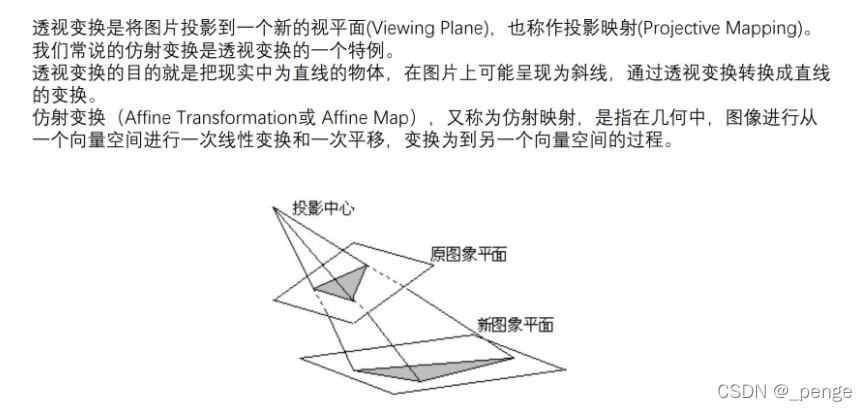




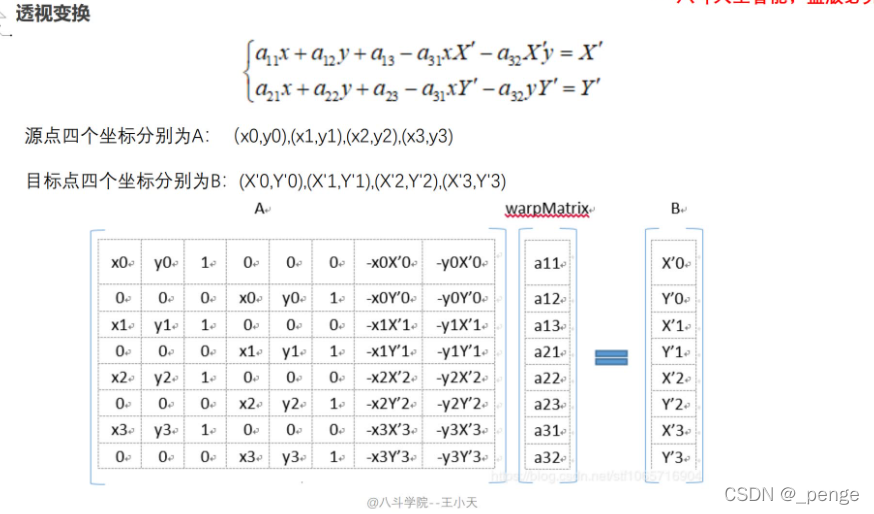
解释：我们的目标是要求出warpMatrix矩阵，所以要找到现图像和将要变化的图像的顶点坐标。因为有8个未知数（3X3的矩阵总共9个参数，我们将A33置为1），所以要找到原坐标和现坐标各4对。带入便可求出warpMatrix矩阵

代码展示

import cv2
import numpy as np

img = cv2.imread('lenna.png')

result3 = img.copy()

'''
注意这里src和dst的输入并不是图像，而是图像对应的顶点坐标。
'''
src = np.float32([[207, 151], [517, 285], [17, 601], [343, 731]])
dst = np.float32([[0, 0], [300, 0], [0, 400], [300, 400]])
print(img.shape)
# 生成透视变换矩阵；进行透视变换
m = cv2.getPerspectiveTransform(src, dst)
print("warpMatrix:")
print(m)
result = cv2.warpPerspective(result3, m, (300, 400))
cv2.imshow("src", img)
cv2.imshow("result", result)
cv2.waitKey(0)

import numpy as np
  
def WarpPerspectiveMatrix(src, dst):
    assert src.shape[0] == dst.shape[0] and src.shape[0] >= 4
     
    nums = src.shape[0]
    A = np.zeros((2*nums, 8)) # A*warpMatrix=B
    B = np.zeros((2*nums, 1))
    for i in range(0, nums):
        A_i = src[i,:]
        B_i = dst[i,:]
        A[2*i, :] = [A_i[0], A_i[1], 1, 0, 0, 0,
                       -A_i[0]*B_i[0], -A_i[1]*B_i[0]]
        B[2*i] = B_i[0]
         
        A[2*i+1, :] = [0, 0, 0, A_i[0], A_i[1], 1,
                       -A_i[0]*B_i[1], -A_i[1]*B_i[1]]
        B[2*i+1] = B_i[1]
  
    A = np.mat(A)
    #用A.I求出A的逆矩阵，然后与B相乘，求出warpMatrix
    warpMatrix = A.I * B #求出a_11, a_12, a_13, a_21, a_22, a_23, a_31, a_32
     
    #之后为结果的后处理
    warpMatrix = np.array(warpMatrix).T[0]
    warpMatrix = np.insert(warpMatrix, warpMatrix.shape[0], values=1.0, axis=0) #插入a_33 = 1
    warpMatrix = warpMatrix.reshape((3, 3))
    return warpMatrix
  
if __name__ == '__main__':
    print('warpMatrix')
    src = [[10.0, 457.0], [395.0, 291.0], [624.0, 291.0], [1000.0, 457.0]]
    src = np.array(src)
     
    dst = [[46.0, 920.0], [46.0, 100.0], [600.0, 100.0], [600.0, 920.0]]
    dst = np.array(dst)
     
    warpMatrix = WarpPerspectiveMatrix(src, dst)
    print(warpMatrix)

应用

透视变换可以将左图栏杆弯曲的部分投影到新的平面，达到呈直线的效果。