• 最常用的两种聚类方法是层次聚类（hierarchical agglomerative clustering）和划分聚类（partitioning clustering）。在层次聚类中，每一个观测值自成一类，这些类每次两两合并，直到所有的类被聚成一类为止。在划分聚类中，首先指定类的个数K，然后观测值被随机分成K类，再重新形成聚合的类。
• 对于层次聚类来说，最常用的算法是单联动（single linkage）、全联动（complete linkage ）、平均联动（average linkage）、质心（centroid）和Ward方法。
• 对于划分聚类来说，最常用的算法是K均值（K-means）和围绕中心点的划分（PAM）。

安装以下软件包： cluster 、 NbClust 、 flexclust 、fMultivar 、 ggplot2 和 rattle ，用于聚类分析。

似乎factoextra这个包在聚类这一块表现很优秀。

聚类分析的一般步骤

11个典型步骤：
1. 选择合适的变量。选择感觉可能对识别和理解数据中不同观测值分组有重要影响的变量。 2. 缩放数据。最常用的方法是将每个变量标准化为均值为0和标准差为1的变量。其他的替代方法包括每个变量被其最大值相除或该变量减去它的平均值并除以变量的平均绝对偏差。执行代码如下：

df1 <- apply(mydata, 2, function(x){(x-mean(x))/sd(x)}) # scale(x, center=T, scale=T)
df2 <- apply(mydata, 2, function(x){x/max(x)})
df3 <- apply(mydata, 2, function(x){(x – mean(x))/mad(x)})

1. 寻找异常点。聚类方法对于异常值是十分敏感的，它能扭曲我们得到的聚类方案。可以通过outliers 包中的函数来筛选（和删除）异常单变量离群点。 mvoutlier 包中包含了能识别多元变量的离群点的函数。
2. 计算距离。两个观测值之间最常用的距离量度是欧几里得距离，其他可选的量度包括曼哈顿距离、兰氏距离、非对称二元距离、最大距离和闵可夫斯基距离（可使用 ?dist 查看详细信息）。默认欧几里得距离。
3. 选择聚类算法。层次聚类对于小样本来说很实用（如150个观测值或更少），而且这种情况下嵌套聚类更实用。划分的方法能处理更大的数据量，但是需要事先确定聚类的个数。
4. 获得一种或多种聚类方法。这一步可以使用步骤5选择的方法。
5. 确定类的数目。尝试不同的类数（比如2～K）并比较解的质量。在 NbClust包中的NbClust() 函数提供了30个不同的指标来帮助进行选择。factoextra包中的fviz_nbclust()来可视化进行聚类选择。（这里更加推荐使用factoextra包来选择，因为其可视化更直观）
6. 获得最终的聚类解决方案。
7. 结果的可视化。层次聚类的结果通常表示为一个树状图。划分的结果通常利用可视化双变量聚类图来表示。
8. 解读类。一旦聚类方案确定，你必须解释（或许命名）这个类。一个类中的观测值有何相似之处？不同的类之间的观测值有何不同？这一步通常通过获得类中每个变量的汇总统计来完成。对于连续数据，每一类中变量的均值和中位数会被计算出来。对于混合数据（数据中包含分类变量），结果中将返回各类的众数或类别分布。
9. 验证结果。 fpc 、 clv 和 clValid 包包含了评估聚类解的稳定性的函数。

计算距离

Euclidean Distance

欧几里得距离(Euclidean Distance)定义：

> head(nutrient)
                energy protein fat calcium iron
BEEF BRAISED       340      20  28       9  2.6
HAMBURGER          245      21  17       9  2.7
BEEF ROAST         420      15  39       7  2.0
BEEF STEAK         375      19  32       9  2.6
BEEF CANNED        180      22  10      17  3.7
CHICKEN BROILED    115      20   3       8  1.4

> as.matrix(dist(nutrient))[1:4,1:4] # 注意提取方式
             BEEF BRAISED HAMBURGER BEEF ROAST BEEF STEAK
BEEF BRAISED      0.00000   95.6400   80.93429   35.24202
HAMBURGER        95.64000    0.0000  176.49218  130.87784
BEEF ROAST       80.93429  176.4922    0.00000   45.76418
BEEF STEAK       35.24202  130.8778   45.76418    0.00000

前两个观测值（ BEEF BRAISED 和 HAMBURGER ）之间的欧几里得距离为：

可见，Euclidean距离很大程度上由能量（ energy ）这个变量控制，因此，这种情况下最好就是scale()后再计算

另外注意混合数据类型的聚类分析
欧几里得距离通常作为连续型数据的距离度量。但是如果存在其他类型的数据，则需要相异的替代措施，你可以使用 cluster 包中的 daisy() 函数来获得包含任意二元（binary）、名义（nominal）、有序（ordinal）、连续（continuous）属性组合的相异矩阵。 cluster 包中的其他函数可以使用这些异质性来进行聚类分析。例如 agnes() 函数提供了层次聚类， pam() 函数提供了围绕中心点的划分的方法。

Gower Distance

gower distance的特别之处在于不仅能够获取纯数值变量的观测之间的距离，还能在观测拥有不同的变量类型如双变量，无序变量，有序变量，数值变量等多种类型变量时，仍然有效。运用cluster包中的diasy()函数并且设置参数metric = "gower"即可获取。其它函数也可以。

dissimilarity <- diasy(x, metric = "gower") # x 为matrix, data frame 等
agnes(dissimilarity) # anges（）对象为diasy()输出或者dist()输出
# 意欲获得最相似（value = 0）与最不相似(value = 1)配对观测位置时
arrayInd(which.min(x), dim(x), dimnames(x))
arrayInd(which.max(x), dim(x), dimnames(x))

Distance计算

• R软件中自带的 dist() 函数能用来计算矩阵或数据框中所有行（观测值）之间的距离。格式是 dist(x, method=)，这里的 x 表示输入数据，并且默认为欧几里得距离。函数默认返回一个下三角矩阵，但是as.matrix() 函数可使用标准括号符号得到距离。
• 另外，cluster包中的daisy()函数在计算观测值距离能力上更强大。因为dist()只能针对numeric类型的数据进行距离计算，而daisy()的metric =可以选择gower对甚至包括多种变量类型的混合类型的观测进行距离计算，并且也只有Gower Distance适用于计算混合类型观测的距离。
• daisy()函数所产生的输出结果其性质与dist()的输出结果是一样性质的。这决定了daisy()的结果可以直接用在很多其它的包中的函数上。比如其对象直接可以用于plot(hclust(daisy()))，也可以在as.matrix后用于factoextra包中的fviz_nbclust()中直接可视化提供选择多少聚类的关键信息。
• 因此，对于单纯numeric变量的数据，计算距离可以直接用dist()，但对于混合型，建议用cluster包中的daisy()。最后通过fviz_nbclust()判定。
• 在fviz_nbclust()的判定参数FUNcluster =中，根据下面要讲的划分聚类分析中的类型来选择。大体上，在整体上用plot()直接观测数据，如果有明显的多中心倾向，则使用PAM，如果不是很明显，则使用Kmeans。详细内容参下。

层次聚类分析

在层次聚类中，起初每一个实例或观测值属于一类。聚类就是每一次把两类聚成新的一类，直到所有的类聚成单个类为止。算法步骤如下： 1. 定义每个观测值（行或单元）为一类； 2. 计算每类和其他各类的距离； 3. 把距离最短的两类合并成一类，这样类的个数就减少一个； 4. 重复步骤(2)和步骤(3)，直到包含所有观测值的类合并成单个的类为止。

下表给出了5种最常见聚类方法的定义和其中两类之间距离的定义：

• 单联动聚类方法倾向于发现细长的、雪茄型的类。它也通常展示一种链式的现象，即不相似的观测值分到一类中，因为它们和它们的中间值很相像。
• 全联动聚类倾向于发现大致相等的直径紧凑类。它对异常值很敏感。
• 平均联动提供了以上两种方法的折中。相对来说，它不像链式，而且对异常值没有那么敏感。它倾向于把方差小的类聚合。
• Ward法倾向于把有少量观测值的类聚合到一起，并且倾向于产生与观测值个数大致相等的类。它对异常值也是敏感的。
• 质心法是一种很受欢迎的方法，因为其中类距离的定义比较简单、易于理解。相比其他方法，它对异常值不是很敏感。但是它可能不如平均联动法或Ward方法表现得好。

层次聚类方法可以用hclust() 函数来实现，格式是hclust(d, method=)，其中 d 是通过dist()函数产生的距离矩阵（也可以是cluster包中daisy()输出），并且方法包括 "single" 、 "complete" 、 "average" 、"centroid" 和 "ward" 。

rownames(nutrient) <- tolower(rownames(nutrient))
plot(hclust(dist(scale(nutrient)), method = "centroid"), hang = -1, cex=.8, main="Average Linkage Clustering") 
#  plot() 函数中的 hang 命令展示观测值的标签（让它们在挂在0下面）。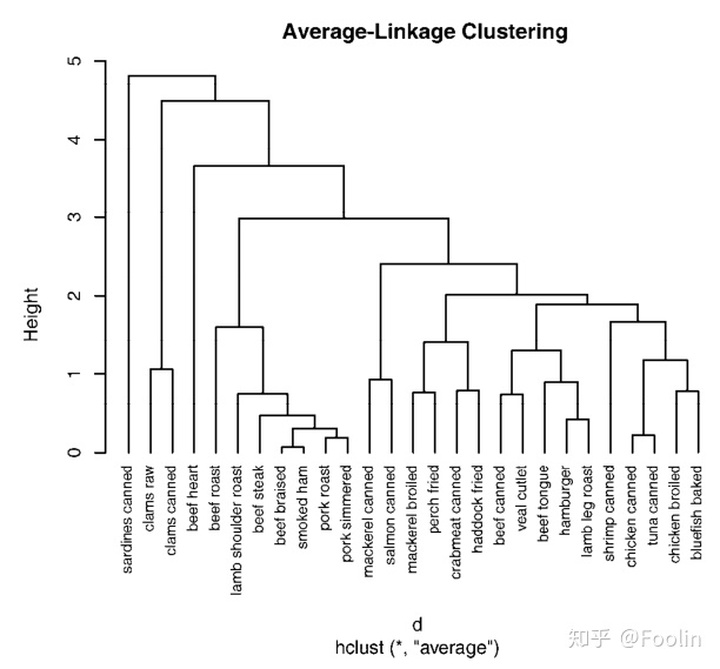

NbClust 包提供了众多的指数来确定在一个聚类分析里类的最佳数目。结果可用来作为选择聚类个数K值的一个参考。

library(NbClust)
devAskNewPage(ask=TRUE)
nc <- NbClust(nutrient.scaled, distance="euclidean", min.nc=2, max.nc=15, method="average")
table(nc$Best.n[1,])
# 0 2 3 4 5 9 10 13 14 15
# 2 4 4 3 4 1 1  2  1  4
barplot(table(nc$Best.n[1,]))

划分聚类分析

在划分方法中，观测值被分为K组并根据给定的规则改组成最有粘性的类。这里讨论两种方法：K均值和基于中心点的划分（PAM）。

K均值聚类（kmeans）

最常见的划分方法是K均值聚类分析。从概念上讲，K均值算法如下： 1. 选择K个中心点（随机选择K行）； 2. 把每个数据点分配到离它最近的中心点； 3. 重新计算每类中的点到该类中心点距离的平均值（也就说，得到长度为p的均值向量，这里的p是变量的个数）； 4. 分配每个数据到它最近的中心点； 5. 重复步骤(3)和步骤(4)直到所有的观测值不再被分配或是达到最大的迭代次数（R把10次作为默认迭代次数）。

K均值聚类能处理比层次聚类更大的数据集。另外，观测值不会永远被分到一类中。当我们提高整体解决方案时，聚类方案也会改动。但是均值的使用意味着所有的变量必须是连续的，并且这个方法很有可能被异常值影响。它在非凸聚类（例如U型）情况下也会变得很差。

在R中K均值的函数格式是 kmeans(x,centers) ，这里 x 表示数值数据集（矩阵或数据框），centers 是要提取的聚类数目。函数返回类的成员、类中心、平方和（类内平方和、类间平方和、总平方和）和类大小。

由于K均值聚类在开始要随机选择k个中心点，在每次调用函数时可能获得不同的方案。使用set.seed() 函数可以保证结果是可复制的。此外，聚类方法对初始中心值的选择也很敏感。kmeans() 函数有一个 nstart 选项尝试多种初始配置并输出最好的一个。例如，加上 nstart=25会生成25个初始配置。通常推荐使用这种方法。

不像层次聚类方法，K均值聚类要求你事先确定要提取的聚类个数。 NbClust 包可以用来作为参考。

data(wine, package = "rattle")
df <-scale(wine[-1])
library(NbClust)
devAskNewPage(ask=TRUE) # 在出图前询问，按enter表示确认
set.seed(123) # 由于kmeans聚类是随机选取行数，因此为保证每次运行结果一致，需setseed()
nc <- NbClust(df, min.nc=2, max.nc=15, method = "kmeans") # 选取2-15, kmeans方法
table(nc$Best.nc[1,])
barplot(table(nc$Best.nc[1,]))

# kmeans聚类
fit.km <-kmeans(df, 3, nstart = 25) # 依据NbClust包选定的centers数作为kmeans分析的基础

# 交叉列表类型（葡萄酒品种）和类成员协议
ct.km <- table(wine$type, fit.km$cluster)
library(flexClust)
randIndex(ct.km) # 兰德指数，用来判定类型变量与类之间的协议
# 0.897

调整的兰德指数为两种划分提供了一种衡量两个分区之间的协定，即调整后机会的量度。它的变化范围是从–1（不同意）到1 （完全同意）。

围绕中心点的划分（PAM）

• 因为K均值聚类方法是基于均值的，所以它对异常值是敏感的。一个更稳健的方法是围绕中心点的划分（PAM）。
• K均值聚类一般使用欧几里得距离，而PAM可以使用任意的距离来计算。因此，PAM可以容纳混合数据类型，并且不仅限于连续变量。

PAM算法步骤如下： 1. 随机选择K个观测值（每个都称为中心点）； 2. 计算观测值到各个中心的距离/相异性； 3. 把每个观测值分配到最近的中心点； 4. 计算每个中心点到每个观测值的距离的总和（总成本）； 5. 选择一个该类中不是中心的点，并和中心点互换； 6. 重新把每个点分配到距它最近的中心点； 7. 再次计算总成本； 8. 如果总成本比步骤(4)计算的总成本少，把新的点作为中心点； 9. 重复步骤(5)～(8)直到中心点不再改变。

可以使用 cluster 包中的 pam() 函数使用基于中心点的划分方法。格式是pam(x, k, metric="euclidean", stand=FALSE)，这里的 x 表示数据矩阵或数据框， k 表示聚类的个数，metric 表示使用的相似性/相异性的度量，而 stand 是一个逻辑值，表示是否有变量应该在计算该指标之前被标准化。

library(cluster)
set.seed(123)
fit.pam <- cluster::pam(wine[-1], k = 3, metric = "euclidean", stand = FALSE)
clusplot(fit.pam, main="Bivariate Cluster Plot")

# 交叉列表类型（葡萄酒品种）和类成员协议
ct.pam <- table(wine$type, fit.pam$cluster)
library(flexClust)
randIndex(ct.pam)
# 0.699

两种方法的比较

比较kmeans与PAM法的randIndex，值越大者表现越优秀，因此，此例中kmeans方法要更好一点。

避免不存在的类

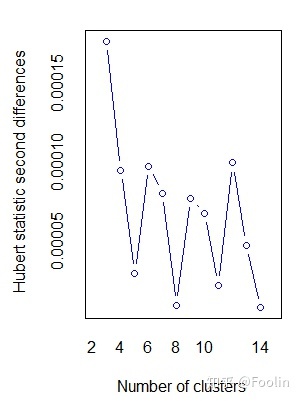
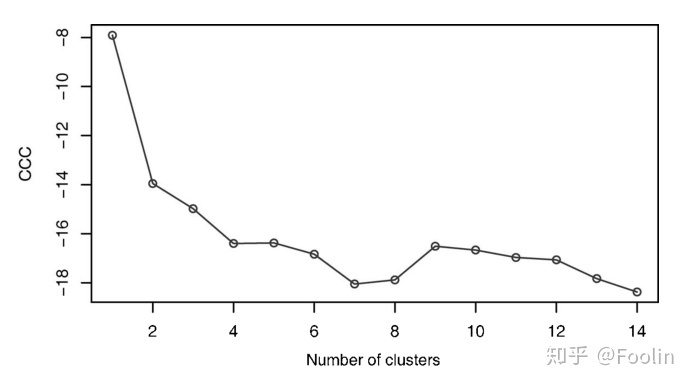
若生成随机数列进行聚类分析，往往无论是层次聚类方法还是划分聚类方法都会进行分类。但实际上是不合适的。此时判定数据是否分类的可能性，可以使用NbClust包自动生成的图来判定，如下，出现如波浪状，说明数据应当有分类。而如图2单一下滑或单峰则显示可能不存在分类。

补充：Jaccard Distance

雅卡尔指数（Jaccard index），又称为并交比（Intersection over Union）、雅卡尔相似系数（Jaccard similarity coefficient），是用于比较样本集的相似性与多样性的统计量。雅卡尔系数能够量度有限样本集合的相似度，其定义为两个集合交集大小与并集大小之间的比例：

雅卡尔距离（Jaccard distance）则用于量度样本集之间的不相似度，其定义为1减去雅卡尔系数，即