训练数据集与测试数据集

KNN算法中，我们是直接将真实数据（有特征有分类）灌到模型中，然后用测试数据与真实数据匹配，从而根据特征的距离计算，可以得到测试数据的预测分类。
因为测试数据的分类是未知的，所以我们没办法来评估我们预测的精准度，即模型的好坏，也就造成了我们对模型的预测结果的可信度无法估计。
因此再实际应用中，我们会将真实数据集按照一定比例分成训练数据集和测试数据集，因为真实的数据集是有真正的特征值以及分类。我们拿到训练数据集训练出来的模型后，用测试数据集进行预测，然后用其预测到的结果和测试数据集的真实分类做对比，便可以衡量出预测的精准度。

代码示例：

#使用鸢尾花实例
import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets

iris = datasets.load_iris()
X = iris.data
y = iris.target

X.shape
#Out：(150, 4)
y.shape
#Out:(150,)

#先将数据打乱，然后取一部分作为测试数据集
## 只乱序index
test_ratio = 0.2 #测试数据集比例
test_size = int(len(X) * test_ratio)

#拆分数据集，乱序后前20%为测试数据集，后80为训练数据集
test_indexes = shuffle_indexes[:test_size]
train_indexes = shuffle_indexes[test_size:]
X_train = X[train_indexes]
y_train = y[train_indexes]

X_test = X[test_indexes]
y_test = y[test_indexes]

Sklearn中的实现，测试KNN算法的准确度

#测试一下KNN算法的准确度
from sklearn.neighbors import KNeighborsClassifier
kNN_classifier = KNeighborsClassifier(n_neighbors=6)
kNN_classifier.fit(X_train,y_train)
y_predict = kNN_classifier.predict(X_test)
y_predict
#Out:array([1, 2, 1, 1, 2, 0, 0, 1, 1, 2, 1, 2, 2, 1, 2, 0, 0, 1, 2, 2, 2, 2,2, 2, 0, 0, 2, 0, 0, 1])

y_test
#array([1, 2, 2, 1, 2, 0, 0, 1, 1, 2, 1, 2, 2, 1, 2, 0, 0, 1, 2, 2, 2, 2,2, 2, 0, 0, 2, 0, 0, 1])

sum(y_predict == y_test)
#Out:29
#预测出30个数据，有29个相等的，则分类准确度是
sum(y_predict == y_test)/len(y_test)
#Out：0.9666666666666667

在Sklearn中预测分类准确度，

from sklearn.metrics import accuracy_score
accuracy_score(y_test,y_predict)
#Out: 0.9666666666666667

有时候我们只希望知道模型的准确度，而不关心模型的预测值，KNN方法中就自带了score方法，只返回分类准确度。

kNN_classifier.score(X_test,y_test)
#Out: 0.9666666666666667

评价分类结果

分类准确度作为评价分类结果的一个参考条件，想要全面的评价分类结果，往往还要引入其他判断标准

混淆矩阵

混淆矩阵是机器学习中总结分类模型预测结果的情形分析表，以矩阵形式将数据集中的记录按照真实的类别与分类模型预测的类别判断两个标准进行汇总。
对于一个二分类问题，所有的问题都被分为0和1类，即是和否
混淆矩阵如下：

	预测值0	预测值1
真实值0	TP	FP
真实值1	FN	TN

我们用positive代表0，negative代表1
根据混淆矩阵我们可以得到4个基本指标：

1.真实值是positive，我们预测为positive的数量，即预测正确（True Positive=TP）
2.真实值是positive，我们预测为negative的数量，即预测错误（False Negative=FN）此错误对应统计学中的第一类错误
3.真实值是negative，我们预测为positive的数量，即预测错误（False Positive=FP）此错误对应统计学的第二类错误
4.真实值是negative，我们预测为negative的数量，即预测正确（True Negative=TN）

混淆矩阵比分类准确度表达的信息更为全面，同时混淆矩阵也衍生出多个指标。

精准率

精准率：$precision=\frac{TP}{TP+FP}$，即预测值是positive，我们预测对了的比例
精准率的来源：
我们通常比较关注我们模型预测对的情况，占比等，比如是否患病，是否有风险等等，所以精准率通常指我们关注的那个事件，预测的有多准

召回率

召回率：$recall=\frac{TP}{TP+TN}$，召回率是指真实值为positive，预测对了的比例，即在我们关注的那个事件真实发生的情况下，我们成功预测的比例是多少。

F1 Score

由于精准率和召回率在有些场景下都需要关注，所以这两个指标组合衍生出了F1 Score，F1 Score是精准率和召回率的调和平均值。
$$F1=\frac{2\ast precision\ast recall}{precision+recall}$$
调和平均值的特点是：如果两者极度不平衡，即一个特别大一个特别小，那调和平均值也会很小，只有当两者都非常高时，它才会很高。

ROC曲线

在了解ROC曲线前，需要先熟悉TPR（True Precision Rate）和FPR（false precision rate）。TPR就是上面说到的召回率，即预测对了的比例；而FPR便是 FP/(TN+FP)，即预测错了的比例。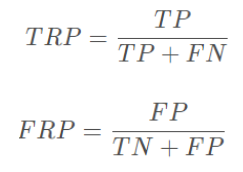

ROC曲线（Receiver Operation Characteristic Cureve）即是描述TPR和FPR之间的关系。x轴是FPR，y轴是TPR。
TPR越大越好，FPR越小越好。如果单一的增大TPR，势必会增加FPR的值，增加了更多预测错误的比例。
ROC曲线呈现的是FPR与TPR之间的关系，我们关注的是曲线下的面积大小(AUC)，面积越大，效果越小，即FPR越小，TPR越大的时候，分类算法就会越好。
如下图，是模型在不同超参数下绘制出的ROC曲线，根据上面，我们可以发现蓝色曲线对应的模型是最好的，因为其AUC最大。对应着就是当FPR为10%的时候，蓝色曲线的TPR最大，为90%。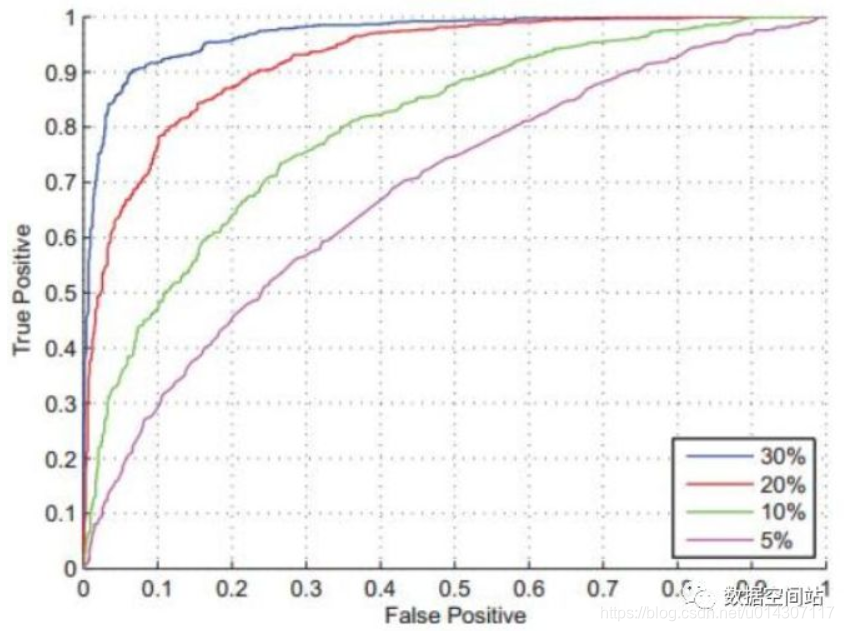

评价回归结果

分类算法有分类准确度，有精准率，召回率，ROC，那么对回归算法而言，都有哪些指标呢？

均方误差MSE

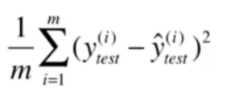
即真实值减去预测值差值的平方均值。由于有对原数据进行了平方，所以会产生量纲的问题，引入RMSE。

均方根误差RMSE

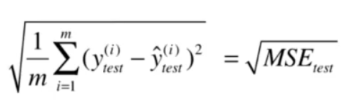
RMSE是对MSE的平方根，消除了量纲的影响。

平均绝对误差MAE

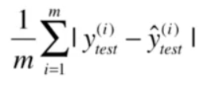
MAE是直接对真值和预测值差值绝对值的均值。

RMSE和MAE的区别？

RMSE和MAE一样，有时候RMSE会大于MAE，这是由于RMSE是将错误差值平方后再开根号。如果错误值本身就很大，则平方后就更大。

所以，RMSE有放大错误值中最大错误的趋势，所以我们一般会让RMSE尽可能的小，意义会更大。

R方 R-Square

MSE/RMSE/MAE都只是对预测结果做一个差值的呈现，如果将模型用于两个不同的场景：用来预测房产和预测成绩，差值分别是10万元 和10分，则如何判断模型更适用于哪一个场景？

此时便引入R方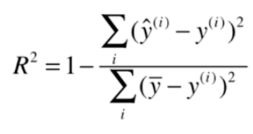

解释一下R方的公式：

分子是：根据训练的模型预测得到的结果和真值结果差值的平方和。

分母是：将y的均值理解为一个基准模型(base model)，即针对所有的数据，预测值都是y的均值。所以分母就是根据基准模型预测得到的结果和真值结果差值的平方和。

用1减去，则可以衡量模型基于基准模型的好坏程度：

R方=1，此时分子趋于0，表示模型的数据与真值相差无几，不犯任何错误。

R方=0，此时分子与分母相近，表示模型和基准模型差不多。

R方<0，此时说明我们的模型还不如基准模型，也可能是数据不存在任何线性关系。

参考

评价分类结果（上）
评价分类结果（下）:F1 Score、ROC、AUC
4.4.2分类模型评判指标（一） - 混淆矩阵(Confusion Matrix)