python 相关性检验怎么计算p值_机器学习:数据的准备和探索——数据假设检验...
图 | 源网络文 | 5号程序员数据假设检验是数理统计学中根据一定假设条件由样本推断总体的一种方法。那我们啥时候会用到假设检验呢?大多数情况下,我们无法分辨事物的真伪或者某种说法是否正确,这时就需要进行假设,然后对我们的假设进行检验。比如,我们想知道被告人是不是有罪,就可以通过假设检验进行判断。基本思路包括4步逻辑:问题是什么?→证据是什么?→判断标准是什么?作出结论。首先,我们要明确问...


数据假设检验是数理统计学中根据一定假设条件由样本推断总体的一种方法。
那我们啥时候会用到假设检验呢?
大多数情况下,我们无法分辨事物的真伪或者某种说法是否正确,这时就需要进行假设,然后对我们的假设进行检验。
比如,我们想知道被告人是不是有罪,就可以通过假设检验进行判断。
基本思路包括4步逻辑:
问题是什么?→证据是什么?→判断标准是什么?作出结论。
首先,我们要明确问题是什么。
问题:检验被告人是否有罪。
根据这个问题,我们可以提出两个互为相反的假设:
零假设:被告人没有罪。
备选假设:被告人有罪。
有了假设,接下来需要明确证据是什么。
根据中心极限定理,足够多合理的样本可以代表总体,所以我们要找到合理的样本数据来做证据。
然后,进一步明确判断标准,绝不能冤枉一个好人,但也不可放过一个坏人。
因为我们定的零假设是:被告人没有罪。所以这里定的标准是,如果被告人没有罪的概率<=5%,那么就直接否定了零假设,也就是被告人没有罪不成立。
这里听着不太顺,被告人没有罪的概率<=5%,其实就是被告人有罪的概率大于95%,所以被告人有很大可能性有罪,因此把零假设否定了。
这里用于做出决策的标准5%,在假设检验里叫做“显著水平”,用符号α(Alpha)表示,是一个概率值。
最后,被告人到底有没有罪呢?
根据样本证据计算出的p值与判断标准α比较下就可以了:
如果p< =α,那么拒绝零假设,也就是备选假设成立;
如果p>α,那么零假设成立。
这就是数据假设检验的基本思路,是我们探索数据的重要部分。
从案例中可以看出,P值是判断的关键。若P值很小,如P<0.05,就可以理解为拒绝零假设犯错误的可能性小于5%,即这个可能性发生的概率很小,可以拒绝。
Python也可以进行假设检验,这里给大家介绍4种简单常用的假设检验:数据正态性检验、独立样本t检验、单因素方差分析和相关性检验。
01K-S检验
判断一组数据是否服从正态分布,最有说服力的方法就是使用正态性检验。
K-S检验的零假设和备选假设如下:
零假设:样本的总体分布服从某特定分布(可以指定为正态分布);
备选假设:样本的总体分布不服从某特定分布。
下面就用Scipy库中的stats模块进行K-S检验,代码如下:
importnumpy as npimportmatplotlib.pyplot as pltfromscipy import stats%matplotlibinline%configInlineBackend.figure_format = "retina"frommatplotlib.font_manager import FontPropertiesfonts= FontProperties(fname="C:\Windows\Fonts\SimHei.ttf", size=14)np.random.seed(19)x= stats.norm.rvs(size=100)plt.figure()plt.hist(x,bins=20,color="red")plt.xlabel("x")plt.ylabel("frequenry")plt.title("histplot")plt.show()stats.kstest(x,"norm")在上面的代码中,先使用np.random.seed()指定了生成随机数的种子,再用stats.norm.rvs()生成100个服从正态分布的随机数,然后绘制直方图,最后使用stats.kstest()进行K-S检验。
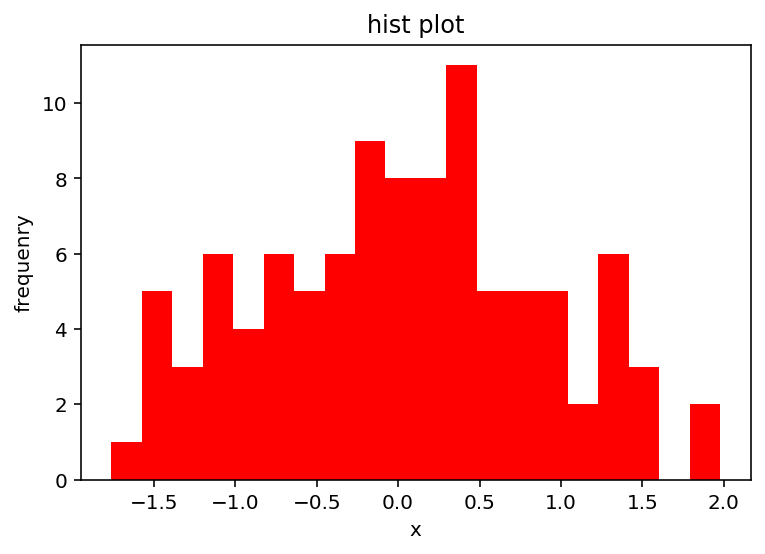
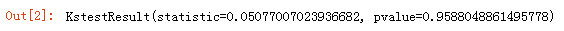
由图像可看出该组数据符合正态分布的钟形。
从输出的检验结果也可以看出,pvalue=0.9588,说明如果拒绝了零假设就有95%的可能性是犯错的,所以不能拒绝零假设,只能认为该组数据是服从正态分布的。
02独立样本t检验
正态性检验是对一组数据分布的检验,那如果有两组数据,需要判断两组数据的平均值是否相等怎么办呢?
可以使用stats.ttest_ind()函数来完成!
独立样本t检验的零假设和备选假设如下:
零假设:两独立样本具有相同的均值;
备选假设:两独立样本的均值不同。
下面用数据举例:
np.random.seed(125)x1= stats.norm.rvs(loc=5,scale=10,size=500)x2= stats.norm.rvs(loc=5,scale=10,size=500)plt.figure()plt.hist(x1,bins=20,color="red",alpha=0.5)plt.hist(x2,bins=20,color="blue",alpha=0.5)plt.xlabel("x")plt.ylabel("frequenry")plt.title("histplot")plt.show()stats.ttest_ind(x1,x2)上面的代码也是先指定随机数种子,然后生成500个均值为5、标准差为10的两组数据x1和x2,最后用stats.ttest_ind()进行独立样本t检验。
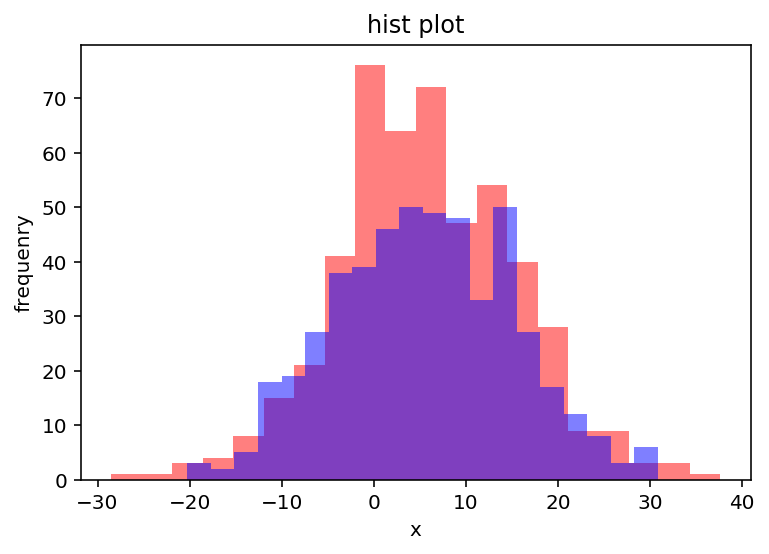
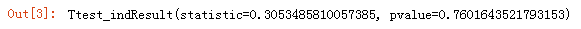
从输出结果可以看出,pvalue=0.7602,p值远大于0.05,说明如果拒绝零假设就有76%的可能性犯错,所以只能接受零假设,即两个独立样本具有相同的均值。
03单因素方差分析
独立样本t检验比较的是两组数据的均值,那如果有好几组数据呢?
面对这种情况,如果想要比较多种因素下各组数据的均值是否有差异,可以使用单因素方差分析,其零假设和备选假设如下:
零假设:各因素的均值相等;
备选假设:各因素的均值不完全相等。
下面我们以鸢尾花数据为例,比较特征sepal_width在3种不同的花下,他们的均值是否相等:
importseaborn as snsimportpandas as pdf= open(r"E:\iris.csv") #每个人文件位置不同Iris= pd.read_csv(f)setosa= Iris["Sepal.Width"][Iris.Species == "setosa"]versicolor= Iris["Sepal.Width"][Iris.Species == "versicolor"]virginica= Iris["Sepal.Width"][Iris.Species == "virginica"]print(stats.levene(setosa,versicolor,virginica))print(stats.f_oneway(setosa,versicolor,virginica))上面的代码先将鸢尾花数据集中的"Sepal.Width"特征分别分给相应的3种花并定义变量。运行后得到结果如下:
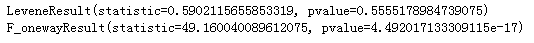
在方差分析之前,首先对3组数据做方差齐性检验(Levene检验),pvalue=0.5555>0.05说明3个数组方差相等,可以进行单因素方差分析。
stats.f_oneway()做单因素方差分析可知pvalue=4.492e-17,远小于0.05,则拒绝零假设,接受备选假设,即3种花的"Sepal.Width"长度不完全相等。
但到这里我们只是知道3种花的"Sepal.Width"长度不完全相等,具体哪些种类不相等我们不知道,这里就可以进行多重比较来获取。
statsmodels.stats.multicomp模块中的pairwise_tukeyhsd()函数就能实现两两变量之间的对比:
fromstatsmodels.stats.multicomp import pairwise_tukeyhsdtukey=pairwise_tukeyhsd(endog=Iris["Sepal.Width"],groups=Iris.Species,alpha=0.05)print(tukey)tukey.plot_simultaneous()
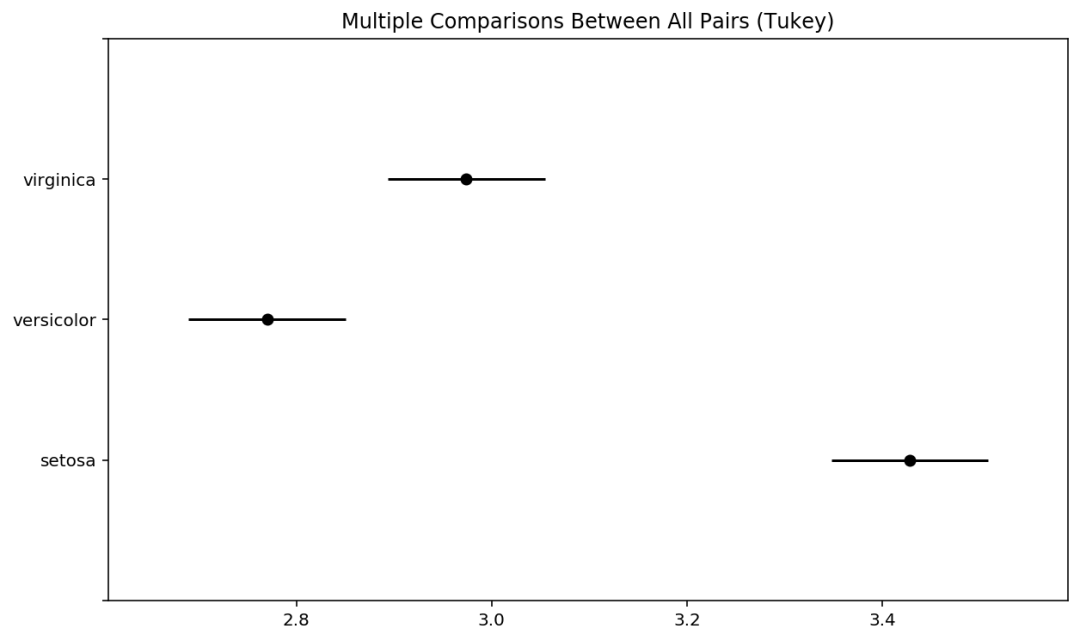
上面输出的结果中,数据表为两两均值比较的结果,最后reject指标都为True,说明3种花两两之间均有差异,并用meandiff列出了差值大小。
第二个图是多重比较中3种花均值所在的位置和置信度为95%的置信区间,由图可知versicolor的平均长度最短,setosa的平均长度最长。
04相关性检验
变量之间的相关性是衡量数据之间是否存在有线性关系的重要属性,检验数据是否具有线性相关可以使用函数stats.pearsonr()函数。
下面仍然以鸢尾花数据为例,对变量sepal_length和petal_length进行皮尔逊相关性检验。
r,pval= stats.pearsonr(Iris["Sepal.Length"],Iris["Petal.Length"])print("相关系数:",r)print("相关系数显著性检验p-value:",pval)输出结果如下:
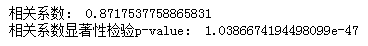
从输出结果可以看出相关系数大小为0.8718,且p-value=1.039e-47远小于0.05,说明线性相关关系成立。
除了上面介绍的4种常用假设检验以外,假设检验的内容还有很多,如卡方检验等,这里就不一一介绍了,感兴趣的小伙伴可以自行查阅相关资料。
下一次,我们将说说数据间的关系,简单的使用Python来分析一些常用的距离度量方式。
你确定不关注我一波?!



更多推荐
 已为社区贡献3条内容
已为社区贡献3条内容







所有评论(0)