权重矩阵的初始化与批归一化

3，权重矩阵的初始化

        深度学习的学习重点就是要根据损失函数训练权重矩阵中的系数。即便如此，权重函数也不能为空，总是需要初始化为某个值。下面我们所要讨论的就是如何初始化这些权重。

3，1 全都初始化为同一个常数可以吗？

        首先要简单回顾一下隐含层中的神经元，他是由权重矩阵中的每行系数与输入x的乘积后接一个非线性函数决定的。 W有多少行，隐藏层就有多少个神经元。

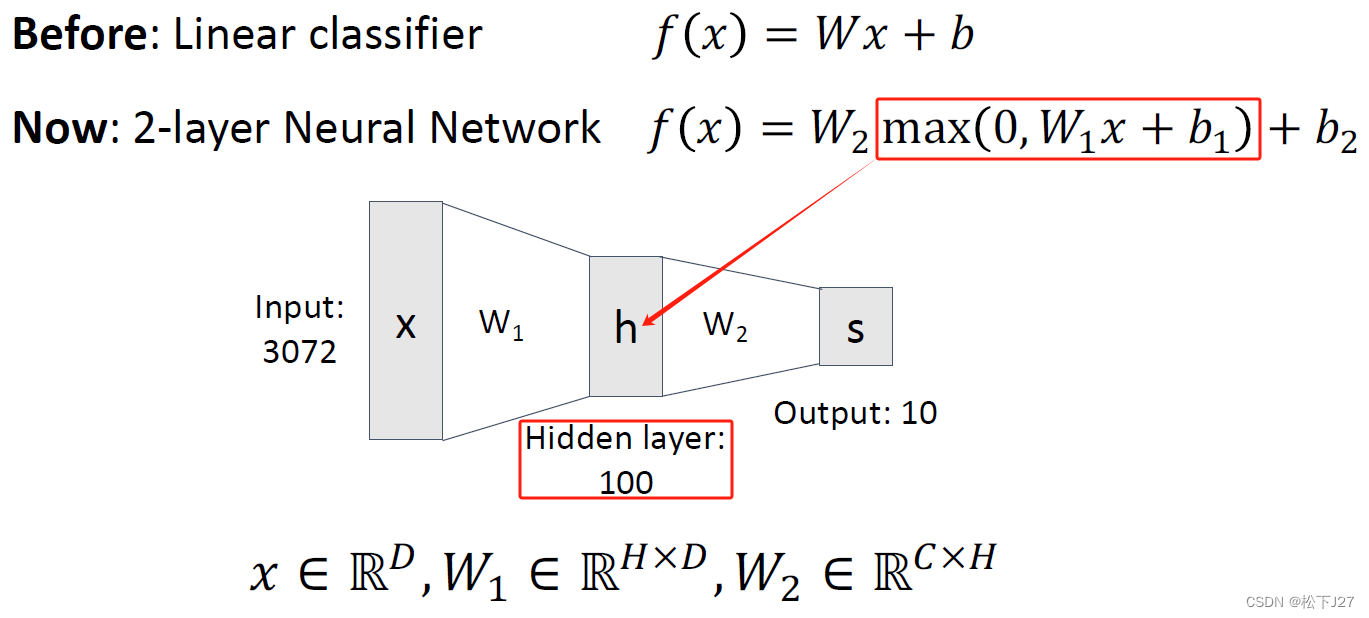
        因此，当矩阵权重W中的所有元素都是同一个常数时，所有神经元的计算结果不论是在前向传播的过程中，还是在反向传播的过程中计算结果都是一样的。如此一来，隐藏层所有的神经元的功效都废了，变成了只有一个神经元。

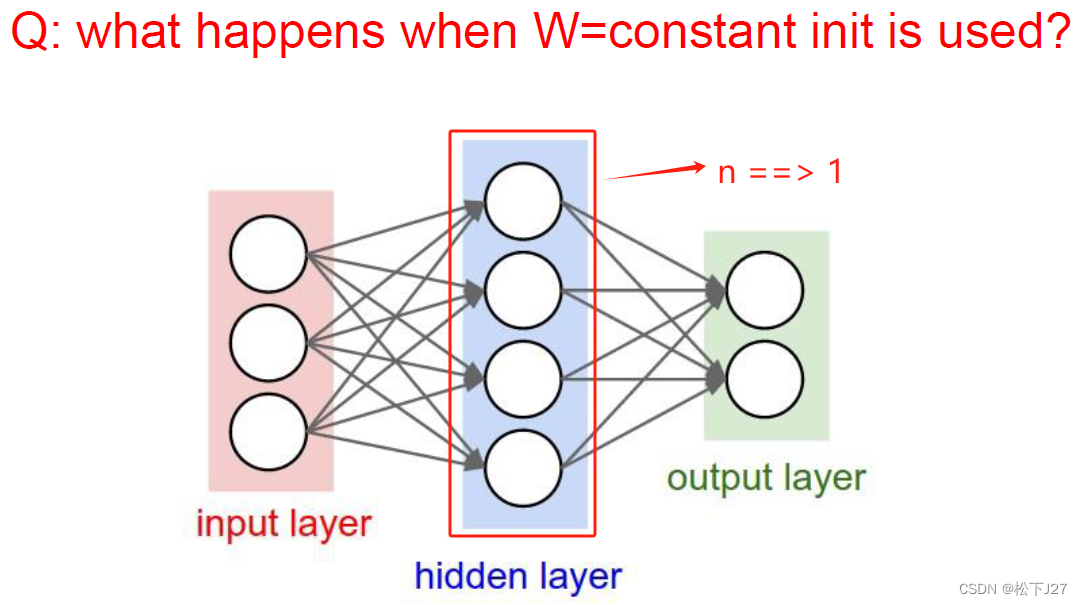
        例如，把W的所有元素都初始化为0。不论有多少个神经元，那么前向传播的计算结果都是0，反向传播的结果都相同。

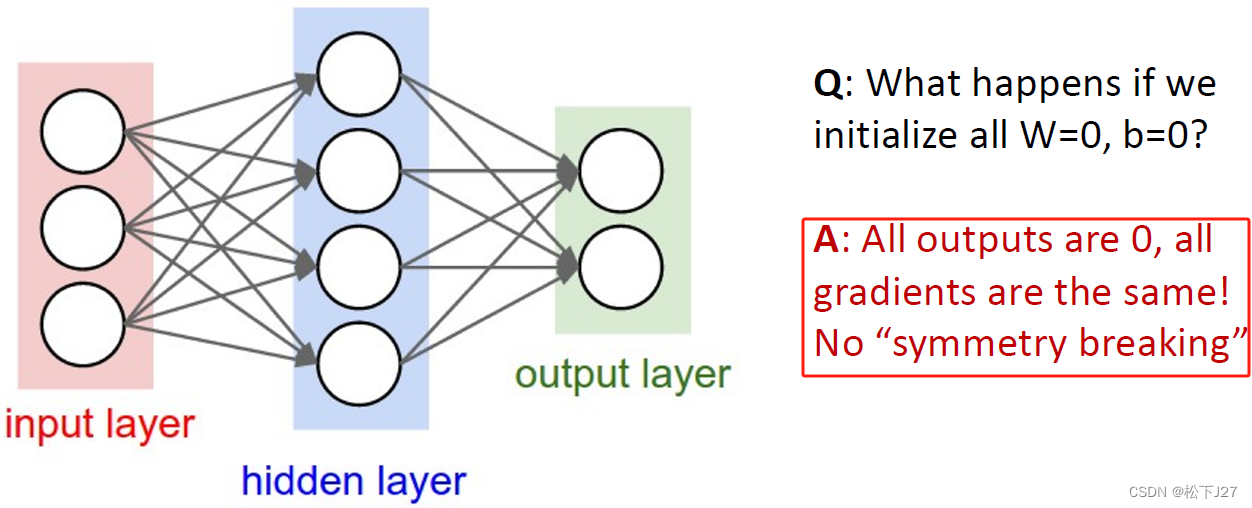
        因此，把所有权重都简单的初始化为同一个数是不行的。 

 3，2 把W初始化为一组较小的随机数

        下面是一个6层的神经网络，有5个隐含层，每层都有4096个神经元。 

        

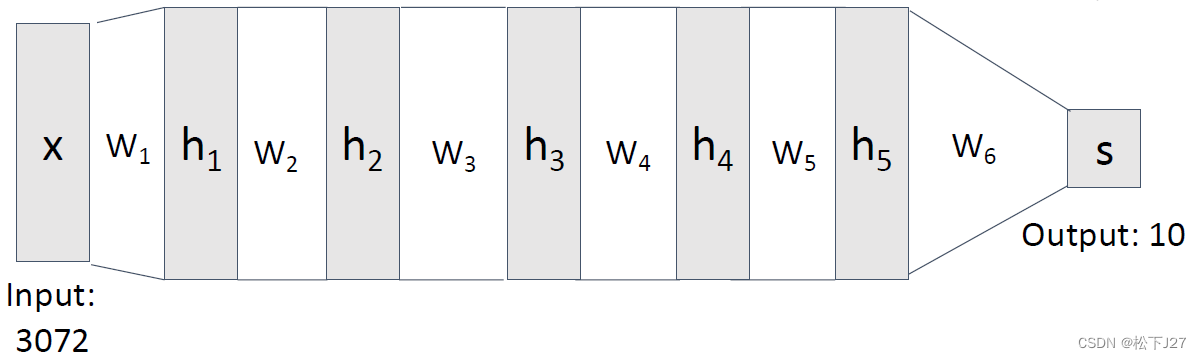
        在初始化的时候把权重矩阵W初始化为均值为0标准差为1的随机数，并且让这组数统一乘以一个很小的数。使用的激活函数为tanh，每层的计算结果也就是神经元的值，保存在hs中。

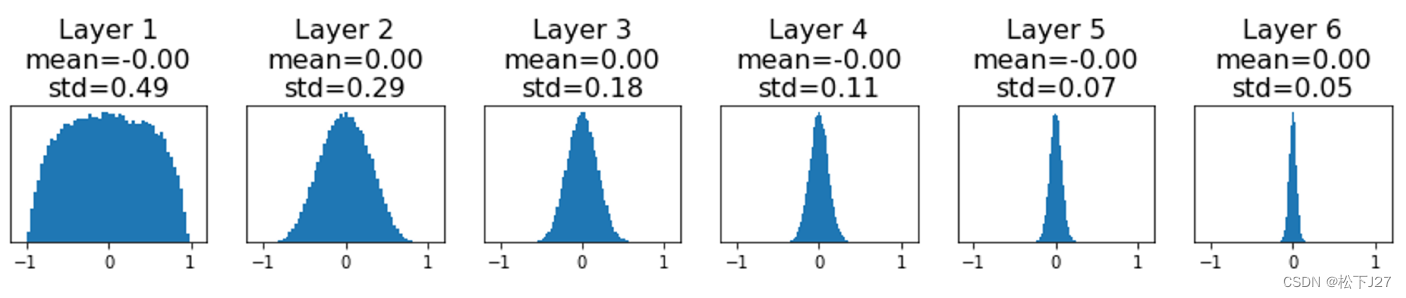
下图是在前向传播的过程中，每层神经元的值的分布： 

        可见随着神经网络的深度越来越深，越来越多的神经元的值会变为0。

对于第i层而言，前向传播的公式为：

x_{i}=tanh(x_{i-1}\cdot W_{i})

        其中x_{i}表示第i层的神经元的值。结合上面的结果来看，当前向传播到很深层的网络后，该层的神经元就几乎全死了。 

此外，在反向传播时，关于第i层的权重W的本地梯度为：

\frac{\partial x_{i}}{\partial W_{i}}=\frac{\partial x_{i}}{\partial tanh(x_{i-1}\cdot W_{i})}\cdot \frac{\partial (x_{i-1}\cdot W_{i})}{\partial W_{i}}=(1-tanh(x_{i-1}\cdot W_{i})^{2})\cdot x_{i-1}

        因此，当深层网络神经元的值(也就是上面公式中的x_{i-1})很多都是0或者趋近于0后，梯度最终会趋于0，即，梯度消失。也就是说，把W初始化为一组较小的随机数也是行不通的。

3，3 把W初始化为一组不太小的随机数

         既然乘以0.01不行(容易出现梯度消失)，何不试一试乘以0.05呢？同样是6层网络，每层同样是4096个神经元，同样是用tanh为激活函数，这次的结果又会如何呢？

         结合每层神经元值的分布来看，出现1和-1的概率比较高。 

\frac{\partial x_{i}}{\partial W_{i}}=\frac{\partial x_{i}}{\partial tanh(x_{i-1}\cdot W_{i})}\cdot \frac{\partial (x_{i-1}\cdot W_{i})}{\partial W_{i}}=(1-tanh(x_{i-1}\cdot W_{i})^{2})\cdot x_{i-1}

        在反向传播的时候容易让1-tanh(x*w)^2为0，即，令local grad本地梯度为0。这也会导致梯度消失！

3，4 如果依然要使用随机数，缩放到什么数量级才合适呢？Xavier

        同样是6层网络，每层同样是4096个神经元，同样是用tanh为激活函数。所不同的是，之前是通过手动调整缩放系数观察神经元值的分布。现在是基于输入的尺寸，自适应的选择缩放系数。这种初始化的方法被称之为Xavier初始化。他有严格的数学证明，其目的是使得每层神经网络在前向传播和反向传播过程中保持方差一致。

        计算结果如下图所示，经过xavier初始化后，所有隐藏层的神经元即不会集中在0附近，也不会徘徊于+-1两端。(对tanh激活函数而言）

 为什么是除以sqrt(Din)?

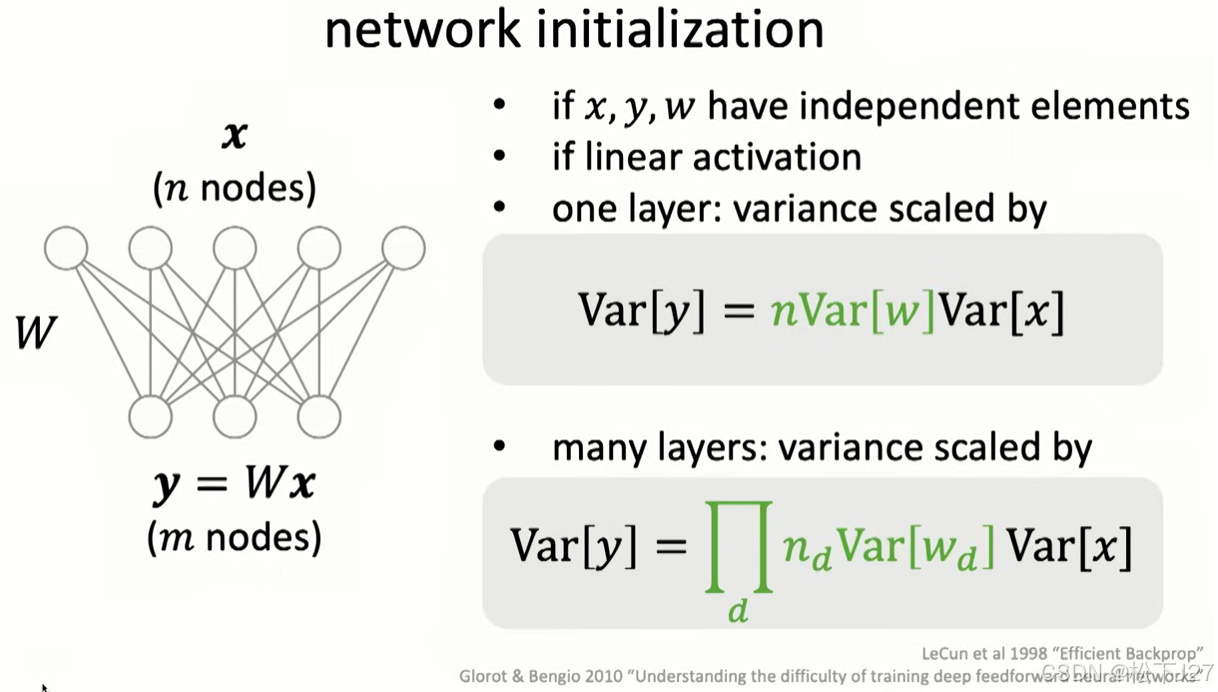
        根据何恺明讲课中的一次课件可以看到：

1，如果x,y,w都是线性独立的

2，如果使用的激活函数为线性激活函数

则每层网络的输出y的方差等于神经元的个数n*权重矩阵w的方差*输入x的方差，即：

var[y]=n*var[w]*var[x]

其中公式中的n就是上面code中的Din。

        随着层数的增加，x的方差不变，但n*var[w]却在不断叠加。因此如果每层的n*var[w]都小于一，则不论是前向传播还是反向传播都会出现梯度消失的现象，如果每层的n*var[w]大于一，则经过多次叠加后，就会出现梯度爆炸的现象。

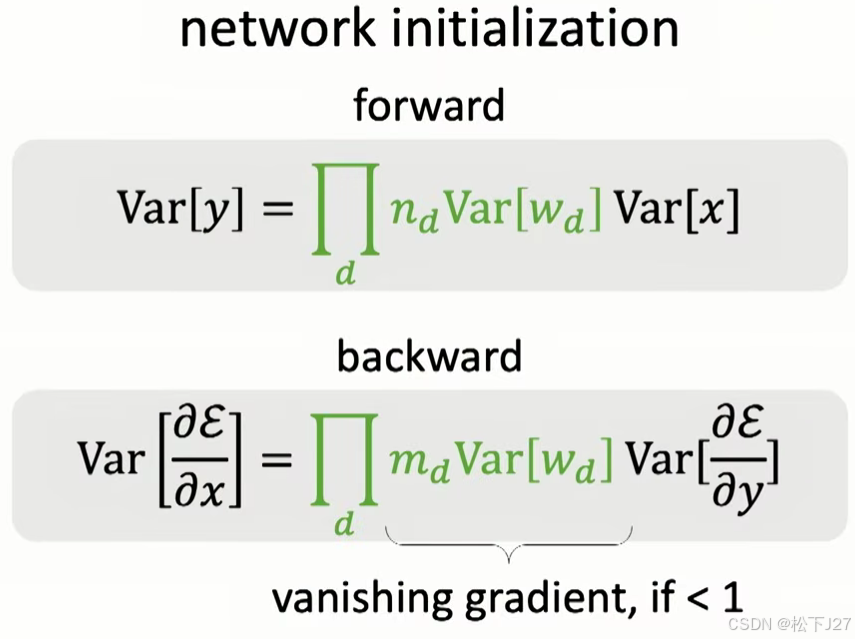
         因此，不论n*var[w]的值为多少，我们始终希望n*var[w]对每层网络的影响为1，这样一来，在经过多层叠加后，就不会出现梯度消失或梯度爆炸。

        Xavier初始化对每层都除以sqrt(Din)应该也是为了达到这一目的而做的努力，所不同的是，在何恺明给出的PPT中，默认使用的是线性激活函数。但本例中的激活函数tanh是非线性激活函数。

3，5 Kaiming初始化/He初始化

        上面提到的Xavier初始化，对于激活函数为tanh的网络是适用的，表现结果也比较好。但当激活函数为ReLU的网络中，依然会出现梯度消失的情况。这是ReLU函数自身天然决定的。

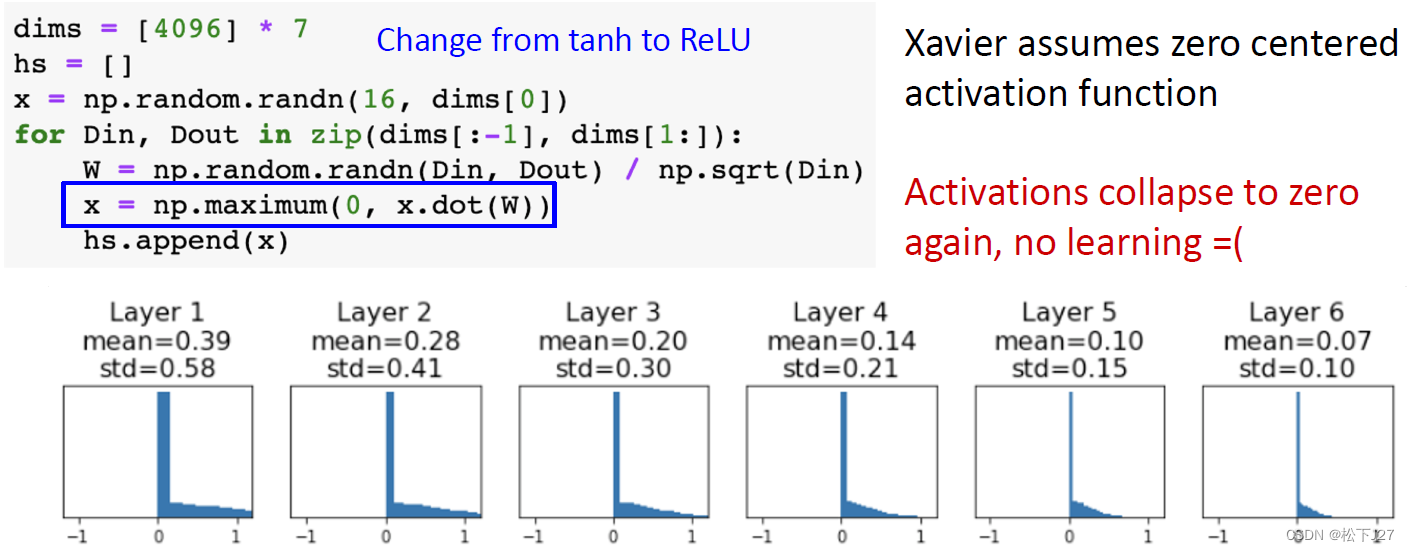
        为了克服这个问题何恺明发明了一种适合ReLU函数的初始化方式。采用kaiming初始化后的后的直方图会分散的更加均匀，而不是集中在0附近。

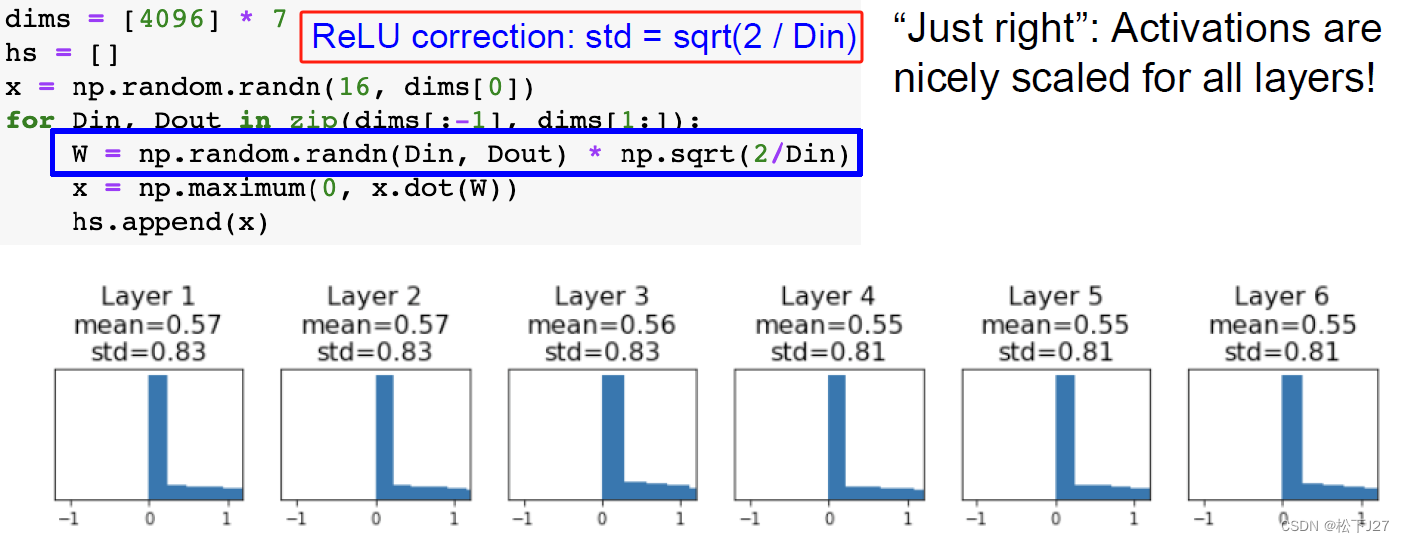
 1/2是怎么来的？

        基于线性激活函数的结果，何恺明发现如果把线性激活函数替换为ReLU函数，则上面的计算结果还要再加一个1/2。

4， 批归一化（Batch Normalization）

        前面讲的初始化权重函数W，主要是通过慎重的选择权重函数W的初值以避免大量神经元的值为0，或集中在+-1。最好能保证神经元值的分布能够尽可能的均等，具体来说，每层神经元值(激活函数的输出)的分布应该尽量朝着以下这些特点努力：

1，0均值。即正负值出现的频次都有，且差不多相同。

2，适当的方差。因为如果方差太大，容易出现梯度爆炸，而方差太小，就会引起梯度消失。Xavier初始化和He初始化就是为了确保每层的激活值方差适当而设计的。

4，1 批归一化的处理对象与维度

        为了达到这一目的，相对于尝试不同初始化W的方法。Batch normalization则着重于处理全连接层的计算结果，也就是对线性变换的输出做二次处理，即对W_{i}x_{i}+b_{i}进行再处理。

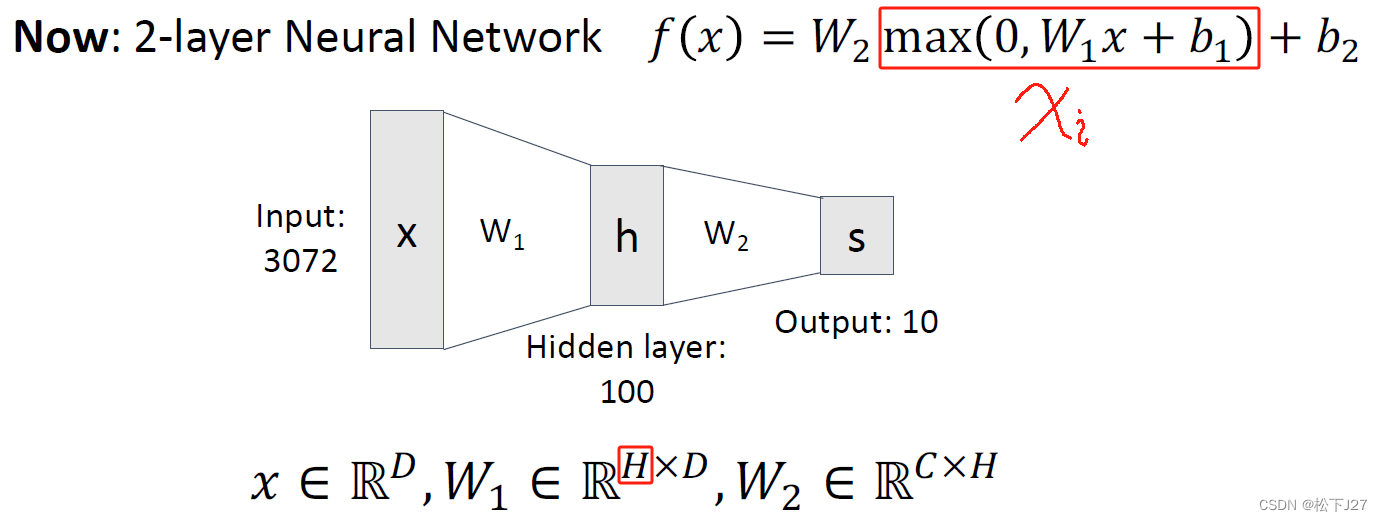
        在下面的这张ppt中，我们看到输入x的维度是NxD，也就是全连接层输出的维度。要搞清楚每个维度代表什么，这里我们可以稍微先回顾一下全连接层。 

         下图为神经网络中的一张PPT，如果说batch normalization中的输入x是W_{i}x_{i}+b_{i}的话，那他的维度就应该等于这里h的维度。h的维度又是由W的其中一个维度决定，他的另一个维度等于前一层的输入。如果是单张图像则输入x的维度为Dx1，W为HxD，输出h的维度为H，H就是神经元的个数。如果输入是N张图，则输入x的维度为DxN，W为HxD，输出h的维度为HxN。

        这也就是说，在batch normalization的PPT中维度是NxD的输入x，其中N表示样本数，D表示神经元的个数。

  4，2 批归一化具体的处理方式

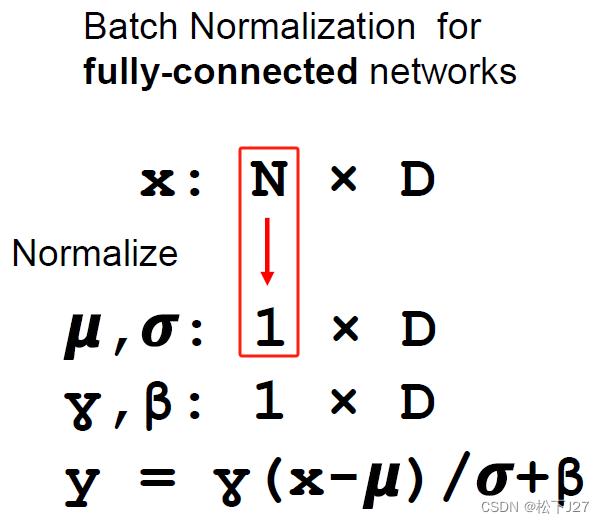
        Batch normalization的做法和前面提过的data preprocessing很像，即，数据减去均值然后再除以标准差（虽然确实存在一些差异）。只不过data preprocessing的对象是最原始的输入数据，而Batch normalization，也叫BN层，是放在全连接层和激活函数之间的。

        与data preprocessing处理数据的不同之处是，除了下图中的第一步完全一样之外。Batch normalization的不同之处在下面图中的第二步中。首先，在除以标准差的时候，为了避免除0，所除的标准差会加上一个很小的数\varepsilon。此外，在减去均值再除以标准差之后，又要再经过一个以\gamma为缩放以\beta为偏置的线性化处理。

 4，2，1 全连接层FC的Batch Normalization

        对于全连接层FC而言，在batch normalization的PPT中输入x的维度是NxD，其中N表示样本数，D表示神经元的个数。Batch normalization的处理是对N个样本求均值：

 4，2，2 CNN卷积层的Batch Normalization 

        对于CNN的卷积层而言，若，输入图像的维度是CinxWxH，共N张图，即NxCxWxH。filter的维度是CinxKwxKh，总共有Cout个filter，即CoutxCinxKwxKh。则输出结果的维度是NxCoutxW'xH'(即下图中输入x的维度)。Batch normalization的处理是对N个WxH的样本求均值： 

4，2，3 全连接层FC的Layer Normalization

        除了Batch normalization以外，类似的，还有一个变种叫Layer Normalization。对于全连接层FC而言，输入x的维度是NxD，其中N表示样本数，D表示神经元的个数。Layer normalization的处理是对D个神经元求均值：

 4，2，4 CNN卷积层的Instance Normalization

        对于CNN的卷积层而言，若，输入图像的维度是CinxWxH，共N张图，即NxCxWxH。filter的维度是CinxKwxKh，总共有Cout个filter，即CoutxCinxKwxKh。则输出结果的维度是NxCoutxW'xH'。Instance Normalization的处理是对WxH的样本求均值： 

（全文完） 

--- 作者，松下J27

增加了关于Xavier初始化与kaiming初始化的说明。2024/07/04

 参考文献(鸣谢)： 

1，Stanford University CS231n: Deep Learning for Computer Vision

2，训练神经网络(第一部分)_哔哩哔哩_bilibili

3，10 Training Neural Networks I_哔哩哔哩_bilibili

4，Schedule | EECS 498-007 / 598-005: Deep Learning for Computer Vision 

5，【中英双语】何恺明教授在MIT开课啦！通俗易懂的深度学习卷积神经网络课程！-机器学习/pytorch_哔哩哔哩_bilibili

（配图与本文无关）

版权声明：所有的笔记，可能来自很多不同的网站和说明，在此没法一一列出，如有侵权，请告知，立即删除。欢迎大家转载，但是，如果有人引用或者COPY我的文章，必须在你的文章中注明你所使用的图片或者文字来自于我的文章，否则，侵权必究。 ----松下J27 

# 深度学习 # 人工智能 # 神经网络
Logo
技术共进，成长同行——讯飞AI开发者社区

技术共进，成长同行——讯飞AI开发者社区

更多推荐

cover

YOLOv8【主干网络篇·第4节】LSKNet大核卷积遥感检测专用网络！

avatar 讯飞AI开发者社区

**发散创新：开源商业中的编程语言探索——以XX语言为例**在开源商业领域，编程语言的选择至关重

本文介绍了XX语言的特点及其在开源电商管理平台项目中的应用。通过实际案例，展示了XX语言在开源商业领域的优势。随着开源商业的不断发展，我们将继续探索更多编程语言在开源项目中的应用，为开发者提供更多有价值的参考。本文将带领大家了解XX语言的特点及其在开源项目中的应用。本文将深入探讨如何在开源项目中合理运用编程语言，并结合XX语言的特点，为大家展示一个充满创新的项目实例。XX语言是一种高效、易学、功能

avatar 讯飞AI开发者社区

人工智能与大数据在2024年医疗健康领域的十大革命性应用场景

而匿名的患者大数据分享平台，则让患有相同疾病的患者能够交换“真实世界”的治疗经验和效果数据，形成宝贵的互助网络，为个体治疗决策提供了强大的社群支持，推动了以患者为中心的医疗模式发展。更重要的是，AI正在辅助设计更安全、高效的CRISPR基因编辑工具，预测编辑脱靶效应，加速基因治疗从基础研究走向临床应用的进程，为根治遗传性疾病开启了新的大门。同时，在供应链管理中，AI可预测药品和医疗物资的需求，实现

avatar 讯飞AI开发者社区