引言：

在机器学习领域，支持向量机（Support Vector Machine，SVM）是一种强大且常用的监督学习算法。它不仅可以用于分类问题，还可以推广到回归分析和异常检测等任务。

一.支持向量机（SVM）算法：

1.基本思想：

支持向量机的基本思想是在高维空间中寻找一个最优超平面来实现数据的分类。这里的“最优”意味着超平面使得不同类别的数据点能够被最大程度地分开，同时保持预测的鲁棒性。其实，SVM就是通过寻找一个距离各类数据点最远的分类边界，来确保分类的准确性和泛化能力。

2.原理：

1.数据映射：

SVM通过核函数将输入数据映射到高维特征空间，使得原本线性不可分的数据在新空间中变得线性可分。

（1）核函数：

在SVM中，核函数起着至关重要的作用，它允许算法在高维特征空间中对非线性数据进行处理。常见的核函数包括线性核、多项式核、高斯核（RBF核）等。核函数的选择对SVM分类器的性能和泛化能力有着显著影响，通过正确选择和调整核函数，我们可以更好地适应不同类型的数据分布。

（2）软间隔与正则化：

软间隔允许部分样本点可以位于分隔超平面的错误一侧，通过引入松弛变量ξi来实现。而正则化参数C则控制了对误分类样本的惩罚程度，C越大表示对误分类的惩罚越严厉，模型对训练数据的拟合越好，但泛化能力可能会受到影响；反之，C越小表示对误分类的惩罚越轻，模型更倾向于选择较大间隔，泛化能力可能更强。

2.寻找最大间隔超平面：

在高维特征空间中，SVM试图找到一个超平面，使得离该超平面最近的样本点到超平面的距离（即间隔）尽可能大。

3.求解支持向量：

在寻找最大间隔超平面的过程中，SVM找到了支持向量，即离超平面最近的那些样本点，它们决定了最终超平面的位置。

3.公式：

（1）核函数：

核函数的形式可以表示为：K(xi, xj) = φ(xi)·φ(xj）

其中φ(·)表示将输入映射到高维空间的映射函数。通过使用核函数，我们可以在不需要显式计算高维特征空间的情况下，直接对高维空间中的内积进行操作，极大地简化了计算复杂度。

（2）支持向量机的优化：

给定训练数据集{(x1, y1), (x2, y2), …, (xn, yn)}，其中xi∈X为输入空间的特征向量，yi∈Y={-1, +1}为特征向量xi的类标记。支持向量机算法的优化问题可以表达为：

min 1/2 ||w||^2 + C∑[i=1,n]{ξi}

约束条件：yi(w∙xi + b) ≥ 1 - ξi, ξi ≥ 0, i=1,2,…,n

其中w为超平面的法向量，b为超平面的截距，ξi为松弛变量，C为惩罚参数。

（3）最大间隔超平面：
 

公式：令 和 位于决策边界上，标签分别为正、负的两个样本， 到分类线的距离为

 到分类线的距离为 则两个异类支持向量到超平面的距离之和为

                              

4.应用领域：

支持向量机算法在实际应用中具有广泛的适用性，包括但不限于文本分类、图像识别、生物信息学、金融预测等领域。在大规模数据和高维特征空间下，SVM仍然保持着较强的性能，并且具有一定的抗噪声能力和泛化能力，因此在实际场景中被广泛应用。

二.代码实现：

（1）数据集部分截图：

（2）代码： 

1.SMO算法：

import numpy as np
import matplotlib.pyplot as plt
# 导入数据集
def load_dataset(file_path):
data = np.loadtxt(file_path)
X = data[:, :-1]
 y = data[:, -1]
    return X, y
# 定义SVM模型
class SVM:
 def __init__(self, C=1.0, tol=0.01, max_passes=10, kernel='linear'):
 self.C = C
 self.tol = tol
 self.max_passes = max_passes
 self.kernel = kernel
# 计算核函数
  def compute_kernel(self, X1, X2):
  if self.kernel == 'linear':
  return np.dot(X1, X2.T)
# 选择第二个变量
def select_update_parameters(self, i, j, X, y, alpha, errors):
pass
# SMO算法的实现
    def smo_algorithm(self, X, y):
        m, n = X.shape
        alpha = np.zeros(m)
        b = 0
        passes = 0
        
while passes < self.max_passes:
   num_changed_alphas = 0
    for i in range(m):
    errors_i = self.compute_error(X, y, alpha, b, i)
 # 判断是否满足KKT条件
    if (y[i] * errors_i < -self.tol and alpha[i] < self.C) or \
      (y[i] * errors_i > self.tol and alpha[i] > 0):
 # 选择第一个变量
    j = self.select_first_variable(i, m)
    errors_j = self.compute_error(X, y, alpha, b, j)
    alpha_i_old, alpha_j_old = alpha[i], alpha[j]
    # 计算上下界
    if y[i] != y[j]:
    L = max(0, alpha[j] - alpha[i])
    H = min(self.C, self.C + alpha[j] - alpha[i])
     else:
     L = max(0, alpha[j] + alpha[i] - self.C)
     H = min(self.C, alpha[j] + alpha[i])
    if L == H:
    continue
    # 计算eta
  eta = 2 * self.compute_kernel(X[i], X[j]) - self.compute_kernel(X[i], X[i]) - self.compute_kernel(X[j], X[j])
     if eta >= 0:
     continue
 # 更新alpha[j]
  alpha[j] -= y[j] * (errors_i - errors_j) / eta
  alpha[j] = np.clip(alpha[j], L, H)
  # 更新alpha[i]
  alpha[i] += y[i] * y[j] * (alpha_j_old - alpha[j])
   # 更新截距b
   b1 = b - errors_i - y[i] * (alpha[i] - alpha_i_old) * self.compute_kernel(X[i], X[i]) - \
y[j] * (alpha[j] - alpha_j_old) * self.compute_kernel(X[i], X[j])
     b2 = b - errors_j - y[i] * (alpha[i] - alpha_i_old) * self.compute_kernel(X[i], X[j]) - \
   y[j] * (alpha[j] - alpha_j_old) * self.compute_kernel(X[j], X[j])
 if 0 < alpha[i] < self.C:
         b = b1
         elif 0 < alpha[j] < self.C:
          b = b2
          else:
          b = (b1 + b2) / 2
          num_changed_alphas += 1
          if num_changed_alphas == 0:
           passes += 1
           else:
                passes = 0
     return alpha, b
# 计算预测值
   def predict(self, X, alpha, b):
        pred = np.sign(np.dot(alpha * y, self.compute_kernel(X, X).T) + b)
        return pred
# 计算预测错误率
    def compute_error_rate(self, pred, y):
        return np.mean(pred != y)
 # 计算预测误差
    def compute_error(self, X, y, alpha, b, i):
        return self.predict(X[i], alpha, b) - y[i]
 # 选择第一个变量
    def select_first_variable(self, i, m):
        j = i
        while j == i:
            j = np.random.randint(m)
        return j
 # 可视化结果
    def plot_decision_boundary(self, X, y, alpha, b):
        x1_min, x1_max = X[:, 0].min() - 1, X[:, 0].max() + 1
        x2_min, x2_max = X[:, 1].min() - 1, X[:, 1].max() + 1
        xx1, xx2 = np.meshgrid(np.arange(x1_min, x1_max, 0.1),
                               np.arange(x2_min, x2_max, 0.1))
        Z = self.predict(np.c_[xx1.ravel(), xx2.ravel()], alpha, b)
        Z = Z.reshape(xx1.shape)
        plt.contourf(xx1, xx2, Z, alpha=0.8)
        plt.scatter(X[:, 0], X[:, 1], c=y, s=20, edgecolors='k')
        plt.xlabel('X1')
        plt.ylabel('X2')
        plt.title('Decision Boundary')
        plt.show()

# 主程序
if __name__ == "__main__":
    # 加载数据
    X, y = load_dataset("D:\Desktop\vocab.txt")

    # 创建SVM模型
    svm = SVM(C=1.0, tol=0.01, max_passes=10, kernel='linear')

    # 运行SMO算法
    alpha, b = svm.smo_algorithm(X, y)

    # 预测结果
    pred = svm.predict(X, alpha, b)

    # 计算错误率
    error_rate = svm.compute_error_rate(pred, y)
    print("Error rate: ", error_rate)

    # 可视化结果
    svm.plot_decision_boundary(X, y, alpha, b)

 结果：

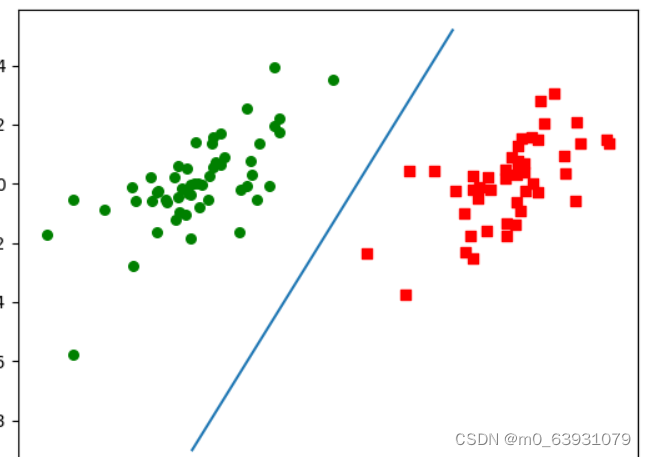
看出svm分类方法分类效果较好，可以较好地分割样本 。

2.垃圾邮件分类：

import numpy as np
from sklearn.feature_extraction.text import CountVectorizer
from sklearn.model_selection import train_test_split
from sklearn.svm import SVC
import matplotlib.pyplot as plt

# 读取文本文件
def read_text_file(file_path):
    with open(file_path, 'r', encoding='utf-8') as f:
        lines = f.readlines()
    return [line.strip() for line in lines]

# 读取数据集
spam_text = read_text_file("D:\Desktop\spamSample1.txt")
ham_text = read_text_file("D:\Desktop\emailSample2.txt")

print('spam_text shape:', np.shape(spam_text))  # (n,)
print('ham_text shape:', np.shape(ham_text))  # (m,)

# 合并文本和标签
all_text = np.concatenate((spam_text, ham_text))
all_labels = np.concatenate((np.ones(len(spam_text)), np.zeros(len(ham_text))))

# 创建标签
spam_labels = np.ones(len(spam_text))
ham_labels = np.zeros(len(ham_text))

# 合并文本和标签
all_text = np.concatenate((spam_text, ham_text))
all_labels = np.concatenate((spam_labels, ham_labels))

# 使用CountVectorizer将文本转换为向量表示
vectorizer = CountVectorizer()
X = vectorizer.fit_transform(all_text)

# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, all_labels, test_size=0.2, random_state=42)

# 使用SMO算法构建SVM分类器
svm = SVC(kernel='linear')
svm.fit(X_train, y_train)

# 在测试集上进行预测
y_pred = svm.predict(X_test)


# 可视化结果
plt.scatter(range(len(y_test)), y_test, color='b', label='Actual')
plt.scatter(range(len(y_test)), y_pred, color='r', label='Predicted')
plt.xlabel('Sample')
plt.ylabel('Class')
plt.legend()
plt.show()

结果： 

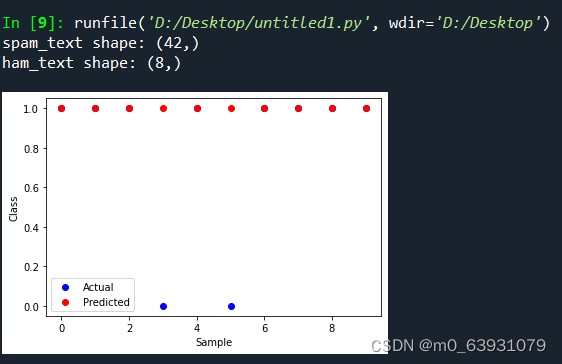
对新的未知邮件进行分类，自动判断是否是垃圾邮件，从结果看出来效果很好。 

（3）SMO算法的优缺点：

1.优点

1.高效性：相对于传统的优化方法，SMO算法在处理大规模数据集时具有较高的效率。它通过在每次迭代中选择两个变量进行优化，使得计算量大幅减少。

2.可行性：SMO算法的每个子问题都能求解闭合解，通过解析方法求解，因此保证了收敛性和可行性。

3.内存利用率高：SMO算法只需要存储一部分的训练样本和其对应的参数，而不需要存储全部的训练数据，因此在处理大规模数据时，占用的内存较少。

4.精度较高：SMO算法对于复杂的非线性问题有较好的表现，并且通过调整参数和核函数的选择，可以得到更好的分类结果。

2.缺点

1.对参数的敏感性：SMO算法中需要选择合适的参数，如惩罚因子C和核函数的参数。这些参数的选择对于SVM的性能和泛化能力至关重要。不恰当的参数选择可能导致过拟合或欠拟合。

2.对数据集特征缩放敏感：由于SMO算法基于计算样本间的内积，所以对于特征的缩放非常敏感。如果特征的取值范围差异较大，建议进行特征缩放（如归一化或标准化处理）。

3.只适用于二分类问题：SMO算法最初设计用于二分类问题，对于多类别分类问题需要进行额外的处理（如一对多策略）。

三.出现的问题及解决方法： 

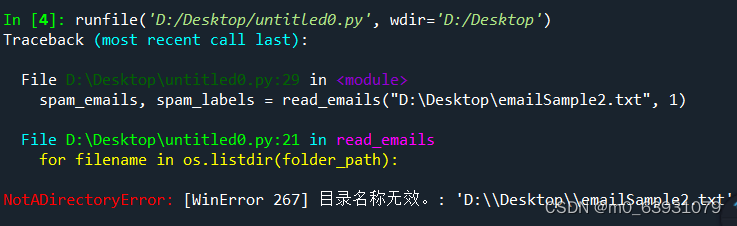
 1.问题：

问题出在调用 read_emails 函数时传递的参数有误。根据报错信息来看，read_emails 函数期望接收一个文件夹路径作为输入，但是这里传递了一个文件路径 ‘D:\Desktop\emailSample2.txt’，导致了 NotADirectoryError 错误。

2.解决方法：

要读取单个文件的内容，可以将 read_emails 函数修改为直接读取单个文件内容的函数，而不是读取文件夹中的多个文件。

四.总结：

通过本次实现，了解到支持向量机算法作为一种强大的分类算法，在实际应用中表现出了较高的性能和鲁棒性。随着大数据和深度学习技术的发展，SVM也在不断演进。近年来，基于SVM的集成学习、多核学习和增量学习等技术逐渐成熟，为SVM的应用拓展了新的可能性。掌握这一重要的机器学习工具，为解决实际问题提供更为可靠和有效的分类方案。