⚠申明： 未经许可，禁止以任何形式转载，若要引用，请标注链接地址。 全文共计3077字，阅读大概需要10分钟
🌈更多学习内容， 欢迎👏关注👀【文末】我的个人微信公众号：不懂开发的程序猿

❗❗❗知识付费，🈲止白嫖，有需要请后台私信或【文末】个人微信公众号联系我

1. RBF神经网络

1.1 RBF网络结构

RBF网络是一种三层前向网络，由于输入到输出的映射是非线性的，而隐含层空间到输出空间的映射是线性的，从而可以大大加快学习速度并避免局部极小问题。多输入单输出的RBF网络结构如图所示。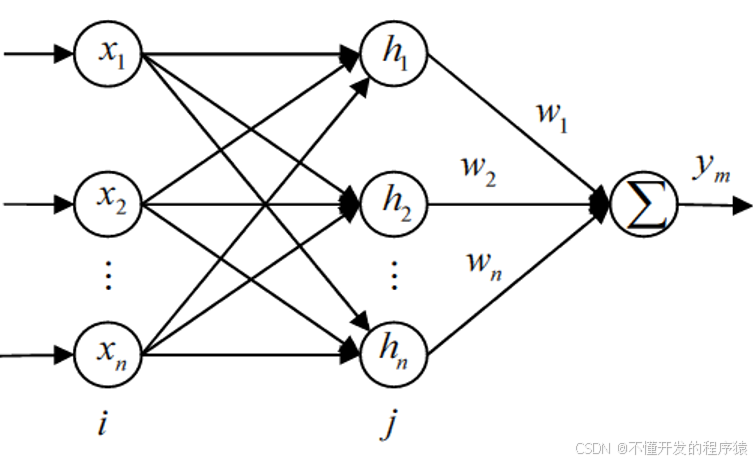

1.2 RBF网络的逼近

RBF神经网络逼近

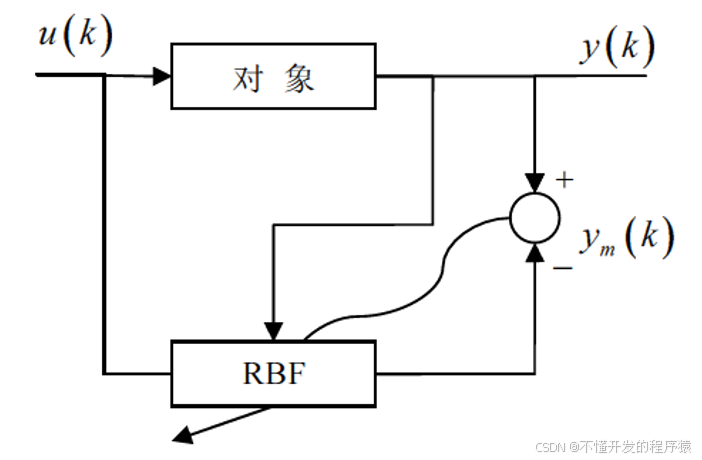
高斯基函数

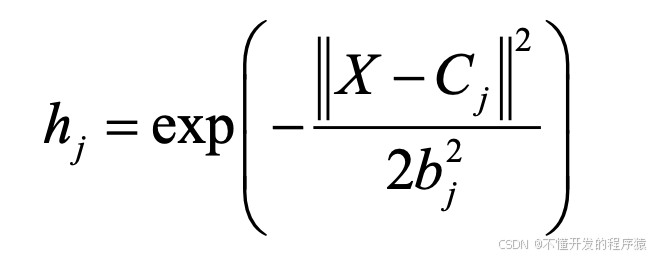
采用RBF网络逼近下列对象

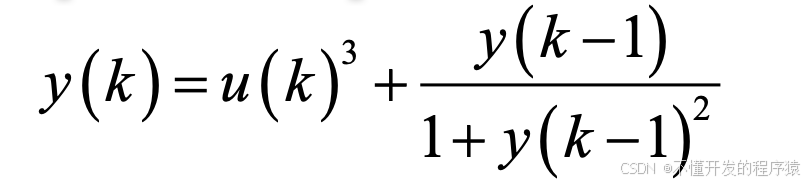
% RBF Network approximation
clc% 清屏
clear all;%删除workplace变量
close all;%关掉显示图形窗口
% 网络学习参数
alfa=0.08; %动量因子
xite=0.7;   %学习因子   
x=[0,0]';

b=1.5*ones(4,1);   
c=0.5*ones(2,4);   
w=rands(4,1);   

w_1=w;
w_2=w_1;
c_1=c;
c_2=c_1;
b_1=b;
b_2=b_1;
d_w=0*w;
d_b=0*b;
y_1=0;

ts=0.001;
for k=1:1:2000
   
    time(k)=k*ts;
    u(k)=0.50*sin(1*2*pi*k*ts);

    y(k)=u(k)^3+y_1/(1+y_1^2);  

    x(1)=u(k); %初值
    x(2)=y(k);

    for j=1:1:4
        h(j)=exp(-norm(x-c(:,j))^2/(2*b(j)*b(j)));% 高斯基函数
    end
    ym(k)=w'*h';
    em(k)=y(k)-ym(k);

    for j=1:1:4
        d_w(j)=xite*em(k)*h(j);
        d_b(j)=xite*em(k)*w(j)*h(j)*(b(j)^-3)*norm(x-c(:,j))^2;
        for i=1:1:2
            d_c(i,j)=xite*em(k)*w(j)*h(j)*(x(i)-c(i,j))*(b(j)^-2);
        end
    end
   w=w_1+ d_w+alfa*(w_1-w_2);
   b=b_1+d_b+alfa*(b_1-b_2);
   c=c_1+d_c+alfa*(c_1-c_2);
   
%%%%%%%%%%%%%%%%%%%Jacobian信息%%%%%%%%%%%%%%%%%%%%
    yu=0;
    for j=1:1:4
        yu=yu+w(j)*h(j)*(c(1,j)-x(1))/b(j)^2; % 敏感度
    end
    dyu(k)=yu;

    y_1=y(k);

    w_2=w_1;
    w_1=w;

    c_2=c_1;
    c_1=c;

    b_2=b_1;
    b_1=b;
end
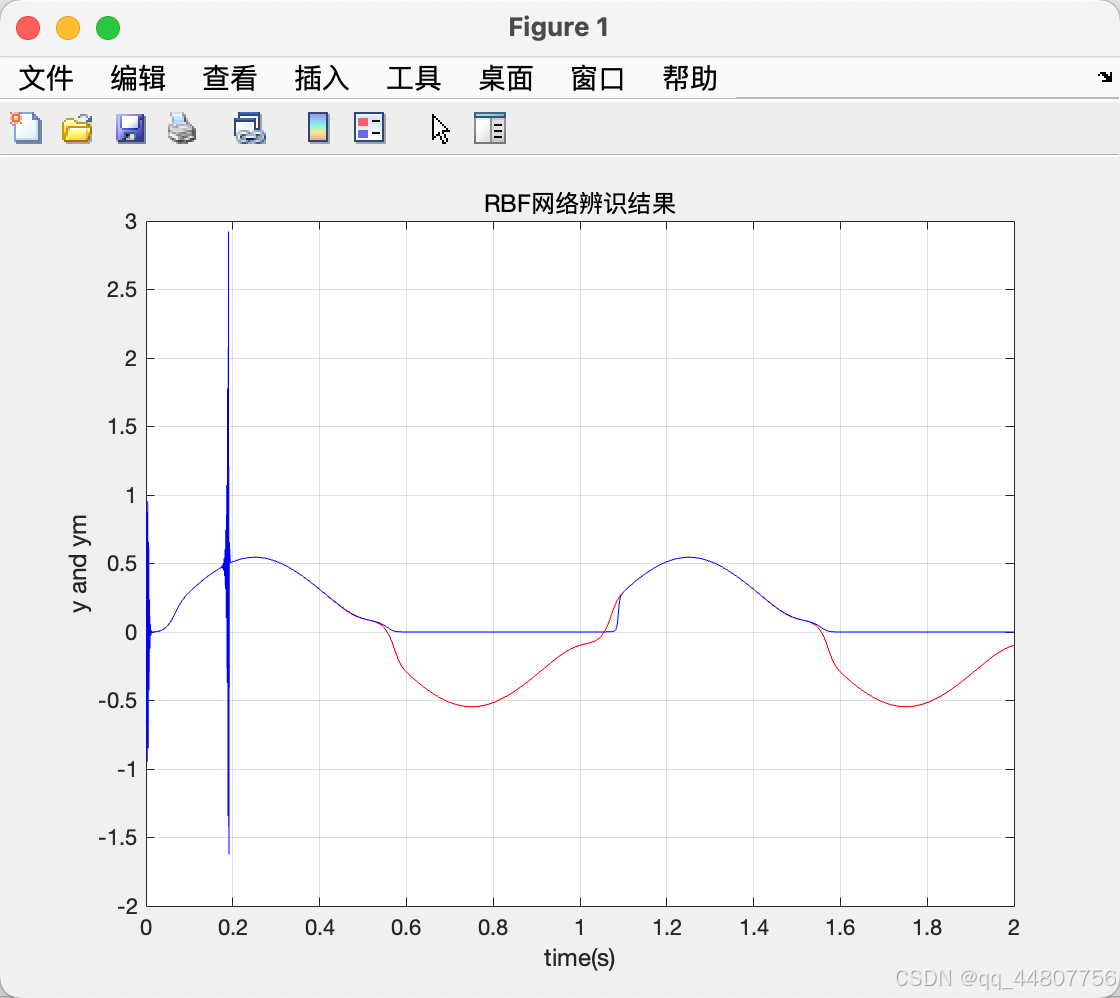
figure(1);
plot(time,y,'r',time,ym,'b'); % RBF网络辨识结果
xlabel('time(s)');ylabel('y and ym');
grid on
title('RBF网络辨识结果')  
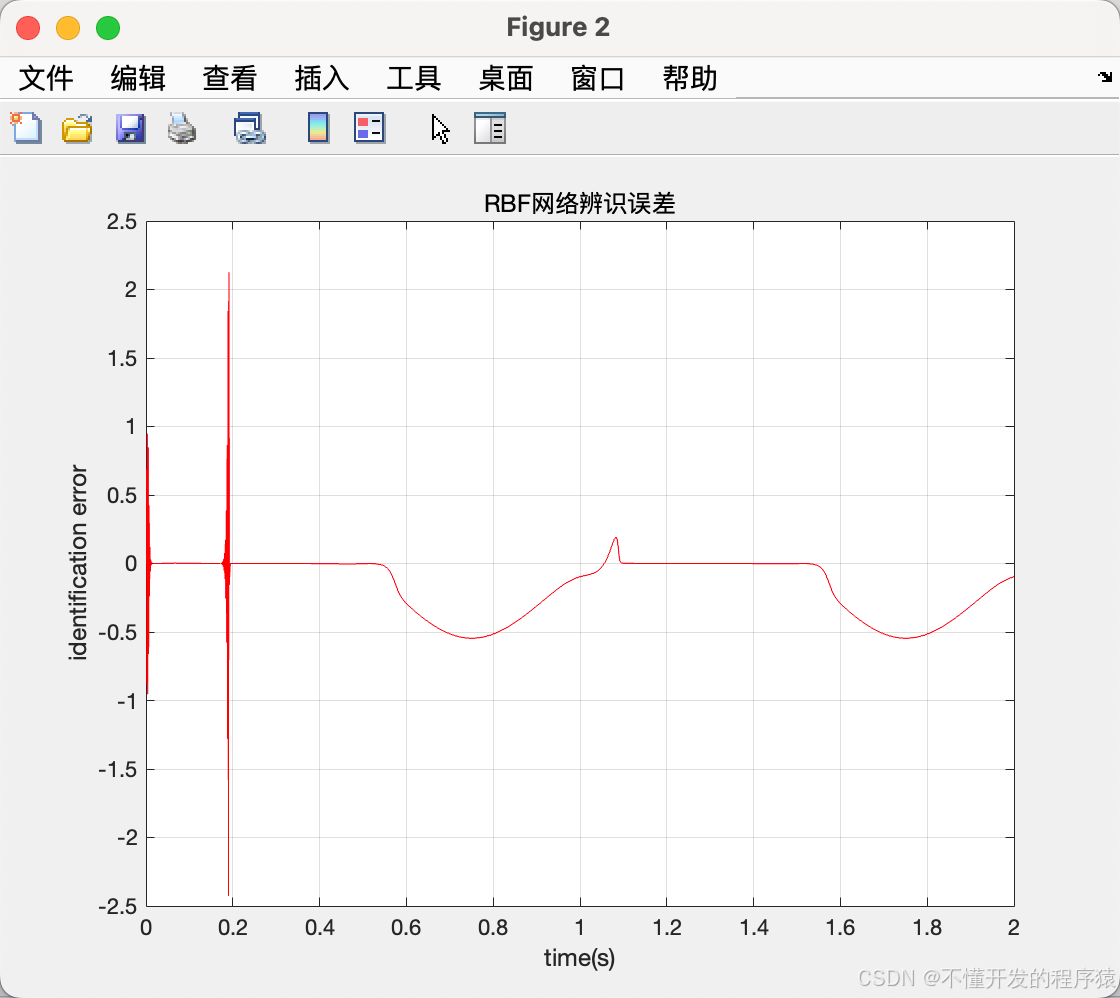
figure(2);
plot(time,y-ym,'r'); % RBF网络辨识误差
xlabel('time(s)');ylabel('identification error');
grid on
title('RBF网络辨识误差')
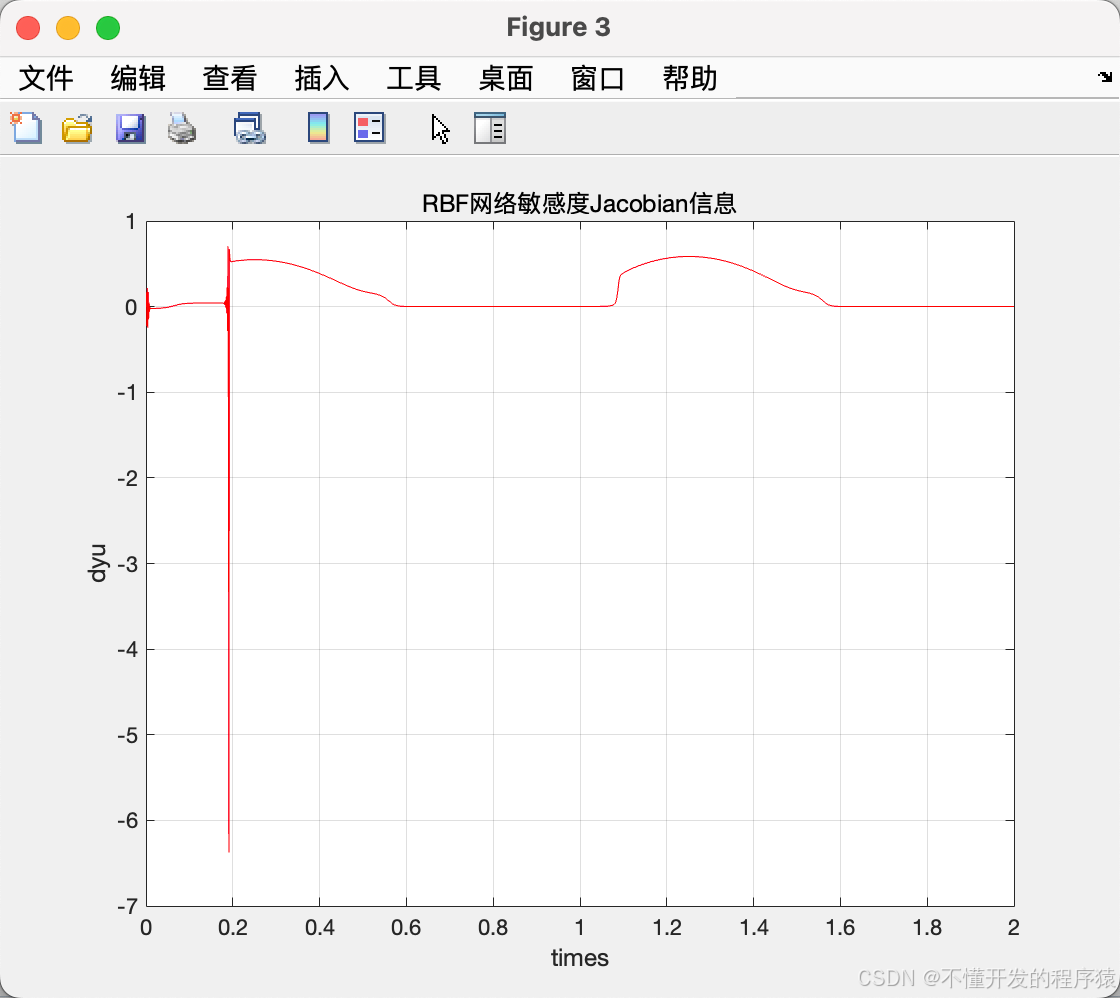
figure(3);
plot(time,dyu,'r');   % RBF网络敏感度Jacobian信息
xlabel('times');ylabel('dyu');
grid on
title('RBF网络敏感度Jacobian信息')

2. 模糊RBF网络

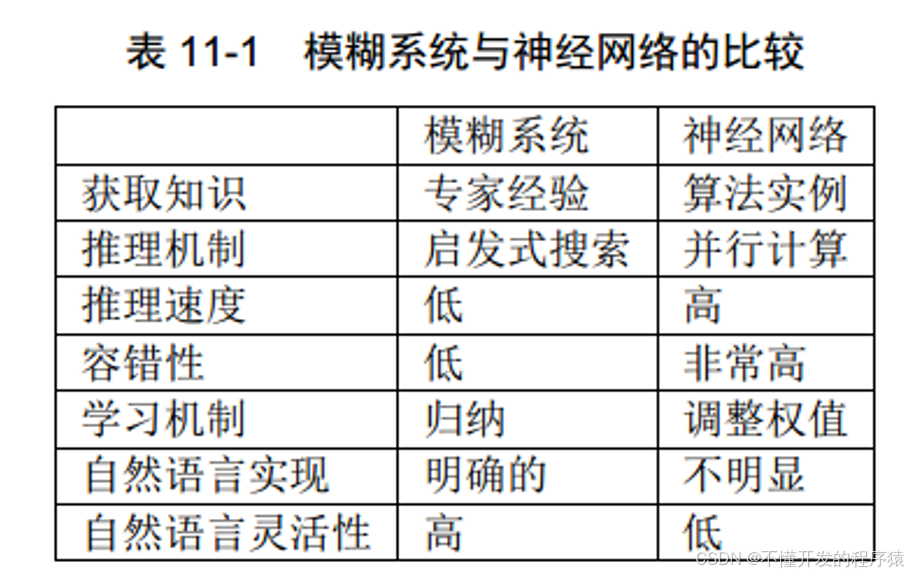
在模糊系统中，模糊集、隶属度函数和模糊规则的设计是建立在经验知识基础上的。这种设计方法存在很大的主观性。将学习机制引到模糊系统中，使模糊系统能够通过不断学习来修改和完善隶属函数和模糊规则，是模糊系统的发展方向。

2.1 网络结构

如图所示为模糊RBF神经网络结构，该网络由输入层、模糊化层、模糊推理层和输出层构成。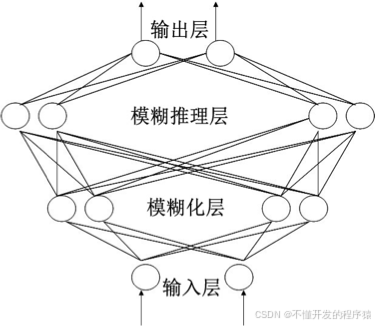

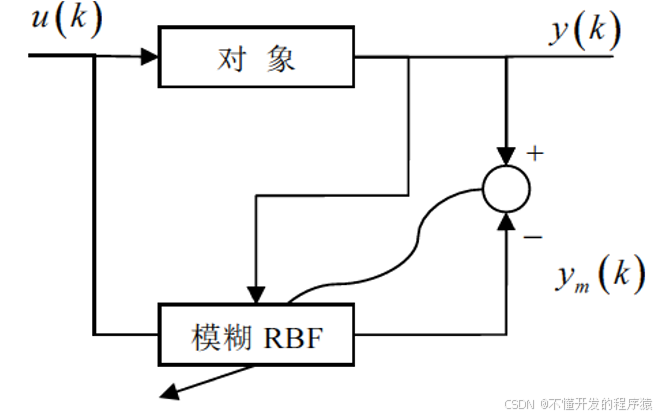
2.2 基于模糊RBF的网络逼近

模糊RBF神经网络逼近

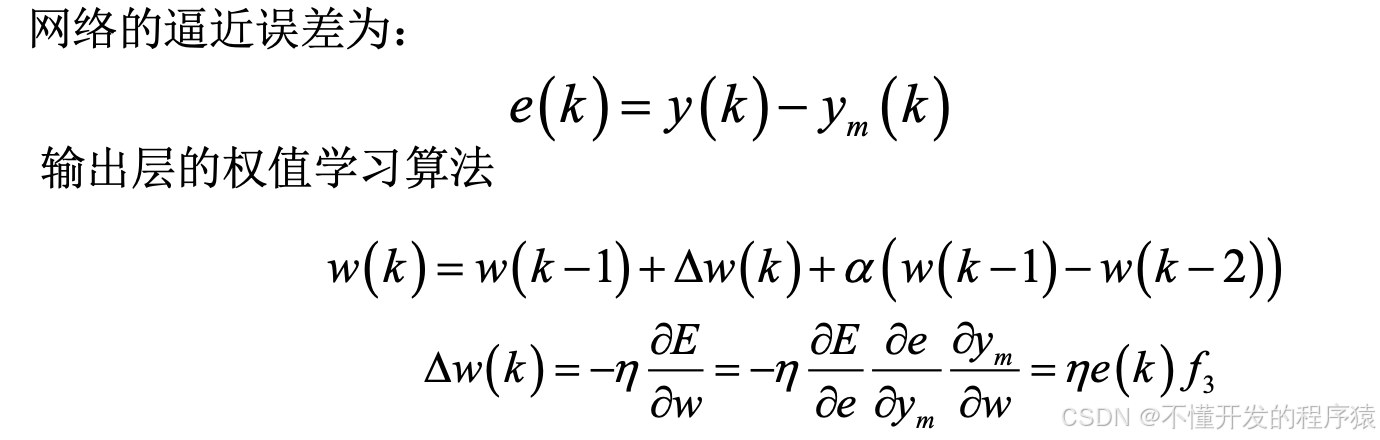
% Fuzzy RBF Approaching
clc % 清屏
clear all; % 删除workplace变量
close all; % 关掉显示图形窗口

xite=0.20; % 学习因子  
alfa=0.05; % 动量因子

b=5*ones(5,1);
c=[-5 -2 0 2 5;
    -5 -2 0 2 5];
w=rands(25,1);

c_1=c;
c_2=c_1;

b_1=b;
b_2=b_1;

w_1=w;
w_2=w_1;

u_1=0.0;
y_1=0.0;

ts=0.001;
for k=1:1:1000
time(k)=k*ts;
   
u(k)=0.5*sin(6*pi*k*ts);
y(k)=u_1^3+y_1/(1+y_1^2);

% Layer1:input
x=[u(k),y(k)]';                     
f1=x;                        

% Layer2:fuzzation
for i=1:1:2                        
   for j=1:1:5
      net2(i,j)=-(f1(i)-c(i,j))^2/b(j)^2;
   end
end
for i=1:1:2
   for j=1:1:5
   f2(i,j)=exp(net2(i,j));
   end
end

% Layer3:fuzzy inference(49 rules)
for j=1:1:5                  
    m1(j)=f2(1,j);
	 m2(j)=f2(2,j);
end

for i=1:1:5
	for j=1:1:5
   	 ff3(i,j)=m2(i)*m1(j);
	end
end
f3=[ff3(1,:),ff3(2,:),ff3(3,:),ff3(4,:),ff3(5,:)];

% Layer4:output
f4=w_1'*f3';                  
ym(k)=f4;                   

e(k)=y(k)-ym(k);

d_w=0*w_1;
for j=1:1:25
    d_w(j)=xite*e(k)*f3(j);
end
w=w_1+d_w+alfa*(w_1-w_2);
 
delta2=-e(k)*w'*f3';;

d_b=0*b_1;
for j=1:1:5
    d_b(j)=xite*delta2*2*((x(1)-c(1,j))^2)*(b(j)^-3);
end
b=b_1+d_b+alfa*(b_1-b_2);
%%%%%
d_c=0*c_1;
for i=1:1:2
    for j=1:1:5
	    d_c(i,j)=-xite*delta2*2*(x(i)-c(i,j))*b(j)^-2;
    end
end
c=c_1+d_c+alfa*(c_1-c_2);
    
   u_1=u(k);
   y_1=y(k);
   
   w_2=w_1;
   w_1=w;
   
   c_2=c_1;
   c_1=c;
   
   b_2=b_1;
   b_1=b;
end
figure(1);
plot(time,y,'r',time,ym,'b');
xlabel('time(s)');ylabel('Approaching');
grid on
title('模糊RBF网络逼近效果')
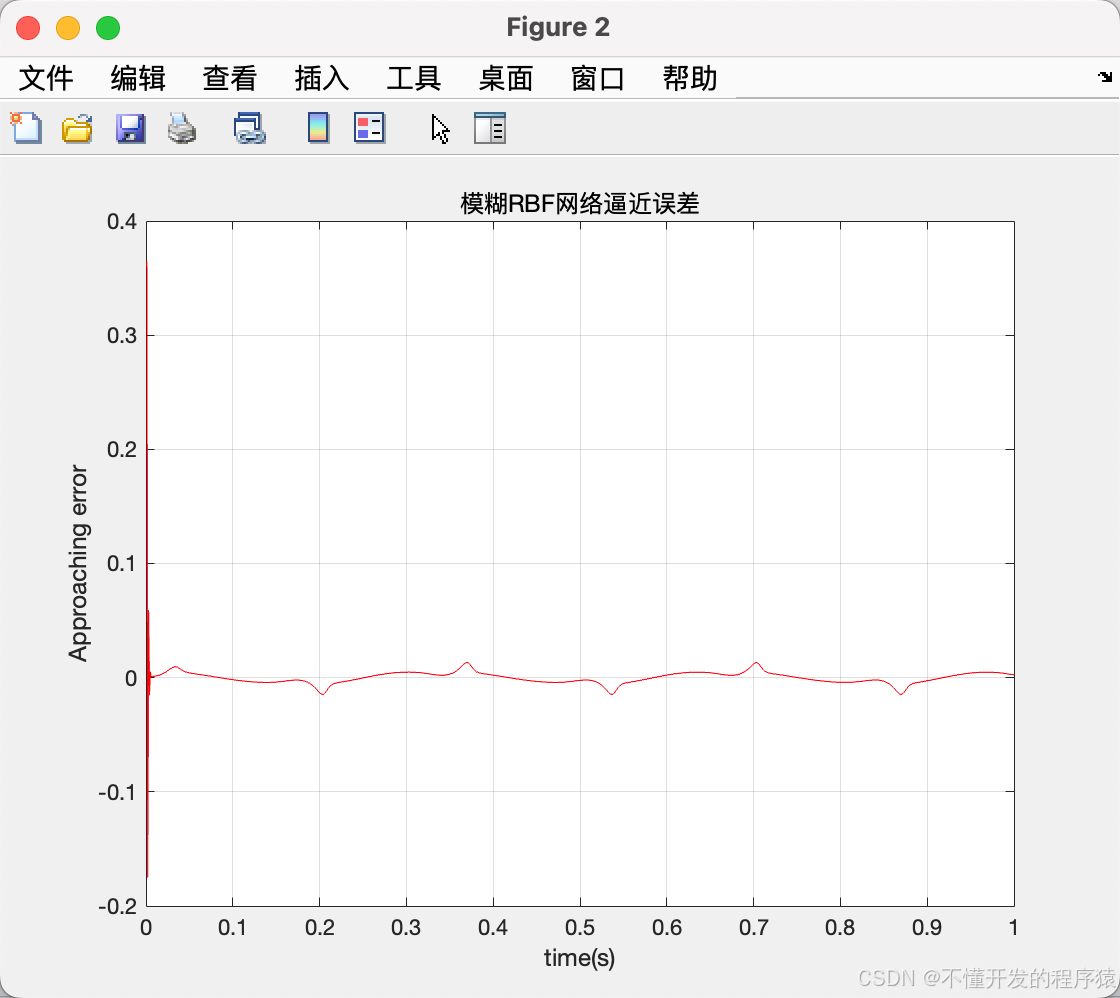
figure(2);
plot(time,y-ym,'r');
xlabel('time(s)');ylabel('Approaching error');
grid on
title('模糊RBF网络逼近误差')

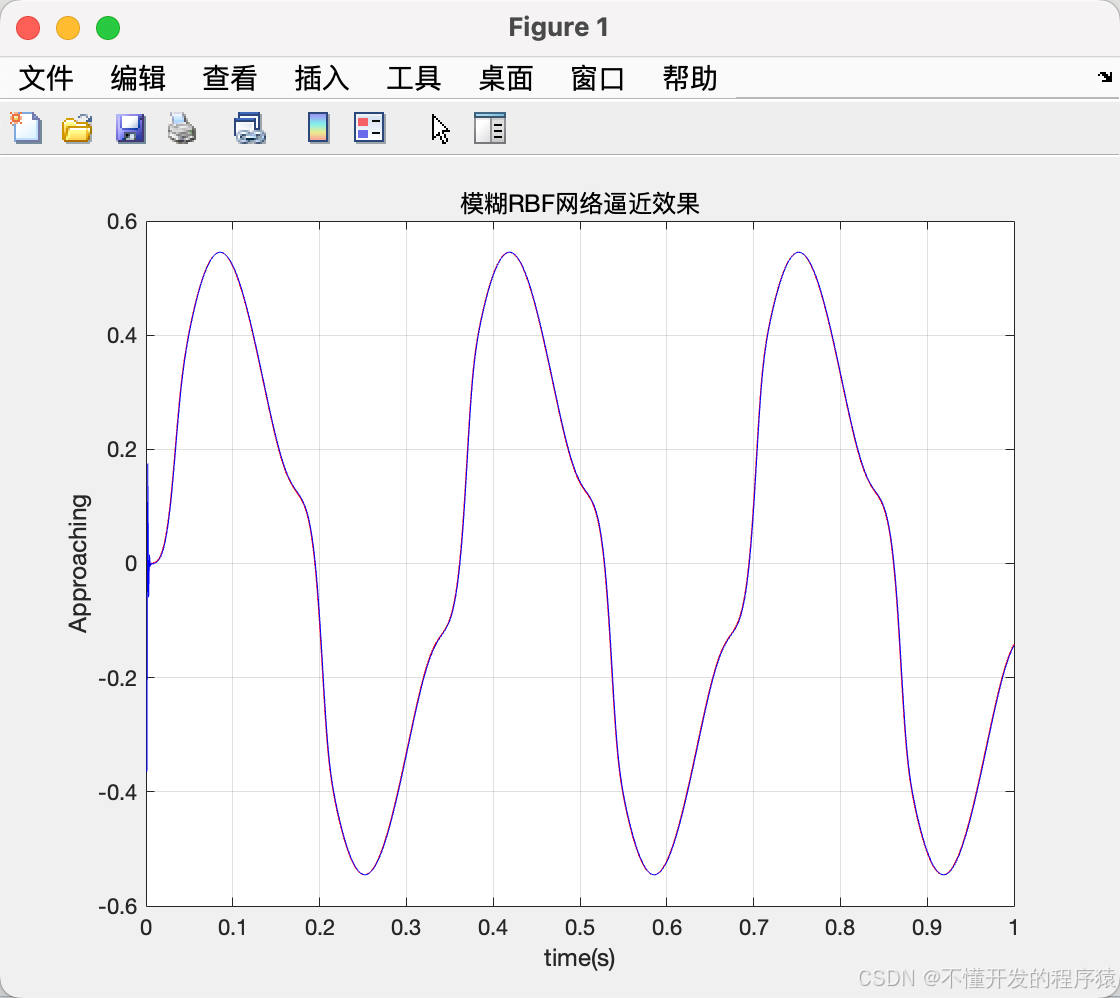
–end–