基于BP神经网络的数据分类
人工神经网络(artificial neural network,ANN)是模仿生物神经网络功能的一种经验模型。生物神经元受到传入的刺激,其反应又从输出端传到相联的其它神经元,输入和输出之间的变换关系一般是非线性的。神经网络是由若干简单(通常是自适应的)元件及其层次组织,以大规模并行连接方式构造而成的网络,按照生物神经网络类似的方式处理输入的信息。模仿生物神经网络而建立的人工神经网络,对输入信号有
⚠申明: 未经许可,禁止以任何形式转载,若要引用,请标注链接地址。 全文共计3077字,阅读大概需要10分钟
🌈更多学习内容, 欢迎👏关注👀【文末】我的个人微信公众号:不懂开发的程序猿❗❗❗知识付费,🈲止白嫖,有需要请后台私信或【文末】个人微信公众号联系我
基于BP神经网络的数据分类
1. BP神经网络基本原理
人工神经网络(artificial neural network,ANN)是模仿生物神经网络功能的一种经验模型。生物神经元受到传入的刺激,其反应又从输出端传到相联的其它神经元,输入和输出之间的变换关系一般是非线性的。神经网络是由若干简单(通常是自适应的)元件及其层次组织,以大规模并行连接方式构造而成的网络,按照生物神经网络类似的方式处理输入的信息。模仿生物神经网络而建立的人工神经网络,对输入信号有功能强大的反应和处理能力。
人脑大约由10^12个神经元组成,神经元互相连接成神经网络。神经元是大脑处理信息的基本单元,以细胞体为主体,由许多向周围延伸的不规则树枝状纤维构成的神经细胞,其形状很像一棵枯树的枝干。它主要由细胞体、树突、轴突和突触组成。如图所示。
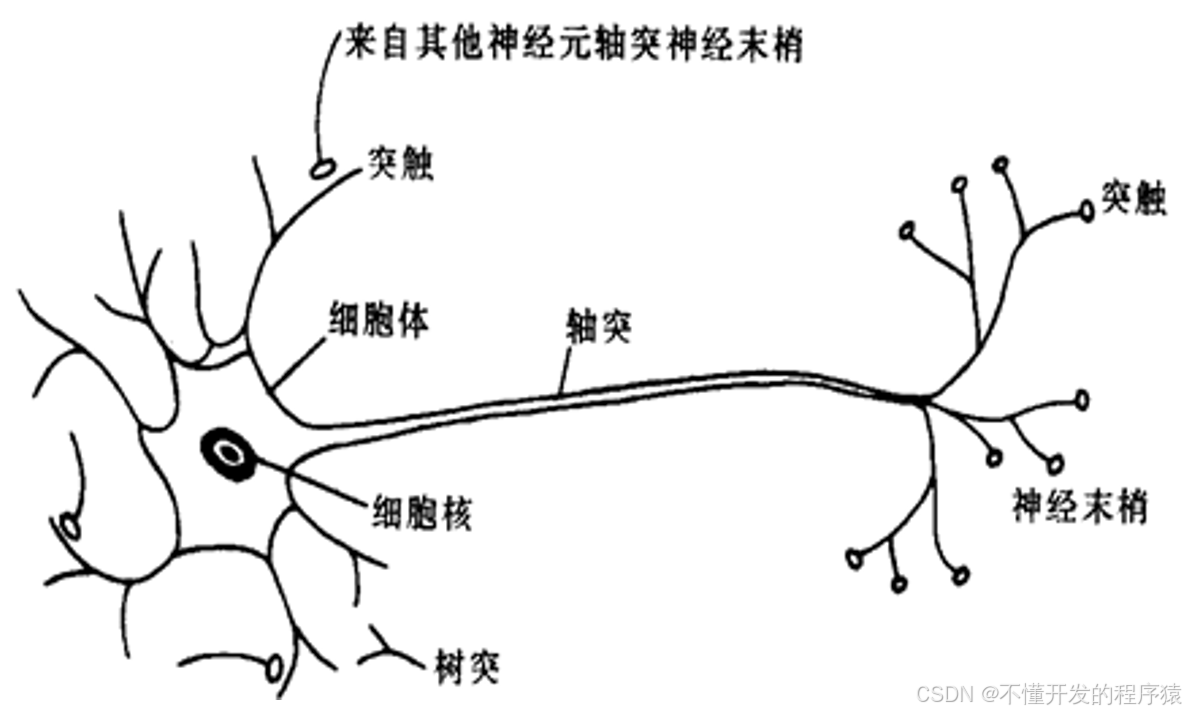
BP(Back Propagation)神经网络是一种神经网络学习算法。其由输入层、中间层、输出层组成的阶层型神经网络,中间层可扩展为多层。相邻层之间各神经元进行全连接,而每层各神经元之间无连接,网络按有教师示教的方式进行学习,当一对学习模式提供给网络后,各神经元获得网络的输入响应产生连接权值(Weight)。然后按减小希望输出与实际输出误差的方向,从输出层经各中间层逐层修正各连接权,回到输入层。此过程反复交替进行,直至网络的全局误差趋向给定的极小值,即完成学习的过程。
2. BP神经网络算法步骤
BP算法是一种有监督式的学习算法,其主要思想是:输入学习样本,使用反向传播算法对网络的权值和偏差进行反复的调整训练,使输出的向量与期望向量尽可能地接近,当网络输出层的误差平方和小于指定的误差时训练完成,保存网络的权值和偏差。
具体步骤如下:
(1)初始化,随机给定各连接权及阀值;
(2)由给定的输入输出模式对计算隐层、输出层各单元输出;
(3)计算新的连接权及阀值;
(4)选取下一个输入模式对返回第2步反复训练直到网络设输出误差达到要求结束训练。
传统的BP算法,实质上是把一组样本输入/输出问题转化为一个非线性优化问题,并通过负梯度下降算法,利用迭代运算求解权值问题的一种学习方法,但其收敛速度慢且容易陷入局部极小,为此一般应用中常采用高斯消元法进行BP网络的学习和训练,即:
对给定的样本模式对,随机选定一组自由权,作为输出层和隐含层之间固定权值,通过传递函数计算隐层的实际输出,再将输出层与隐层间的权值作为待求量,直接将目标输出作为等式的右边建立方程组来求解。
具体步骤如下:
(1)随机给定隐层和输入层间神经元的初始权值。
(2)由给定的样本输入计算出隐层的实际输出。
(3)计算输出层与隐层间的权值。以输出层的第r个神经元为对象,由给定的输出目标值作为等式的多项式值建立方程。
(4)重复第三步就可以求出输出层m个神经元的权值,以求的输出层的权矩阵加上随机固定的隐层与输入层的权值就等于神经网络最后训练的权矩阵。
3. BP网络的语音信号识别
语音特征信号识别是语音识别研究领域中的一个重要方面,一般采用模式匹配的原理解决。语音识别的运算过程为:首先,待识别语音转化为电信号后输入识别系统,经过预处理后用数学方法提取语音特征信号,提取出的语音特征信号可以看成该段语音的模式。然后将该段语音模型同已知参考模式相比较,获得最佳匹配的参考模式为该段语音的识.洲结果。语音识别流程如图所示。

BP神经网络构.建根据系统输人输出数据特点确定BP神经网络的结构,由丁语音特征输入信号有24维,待分类的语音信号共有4类,所以BP神经网络的结构为24-25-4,即输人层有24个节点,隐含层有25个节点,输出层有4个节点。
clc % 清屏
clear all; % 删除workplace变量
close all; % 关掉显示图形窗口
format short
% Initial
%% 训练数据预测数据提取及归一化
%下载四类语音信号
load data1 c1
load data2 c2
load data3 c3
load data4 c4
%四个特征信号矩阵合成一个矩阵
data(1:500,:)=c1(1:500,:);
data(501:1000,:)=c2(1:500,:);
data(1001:1500,:)=c3(1:500,:);
data(1501:2000,:)=c4(1:500,:);
%从1到2000间随机排序
k=rand(1,2000);
[m,n]=sort(k);
%输入输出数据
input=data(:,2:25);
output1 =data(:,1);
%把输出从1维变成4维
for i=1:2000
switch output1(i)
case 1
output(i,:)=[1 0 0 0];
case 2
output(i,:)=[0 1 0 0];
case 3
output(i,:)=[0 0 1 0];
case 4
output(i,:)=[0 0 0 1];
end
end
%随机提取1500个样本为训练样本,500个样本为预测样本
input_train=input(n(1:1500),:)';
output_train=output(n(1:1500),:)';
input_test=input(n(1501:2000),:)';
output_test=output(n(1501:2000),:)';
%输入数据归一化
[inputn,inputps]=mapminmax(input_train);
%% 网络结构初始化
innum=24;
midnum=25;
outnum=4;
%权值初始化
w1=rands(midnum,innum);
b1=rands(midnum,1);
w2=rands(midnum,outnum);
b2=rands(outnum,1);
w2_1=w2;w2_2=w2_1;
w1_1=w1;w1_2=w1_1;
b1_1=b1;b1_2=b1_1;
b2_1=b2;b2_2=b2_1;
%学习率
xite=0.1
alfa=0.01;
%% 网络训练
for ii=1:10
E(ii)=0;
for i=1:1:1500
%% 网络预测输出
x=inputn(:,i);
% 隐含层输出
for j=1:1:midnum
I(j)=inputn(:,i)'*w1(j,:)'+b1(j);
Iout(j)=1/(1+exp(-I(j)));
end
% 输出层输出
yn=w2'*Iout'+b2;
%% 权值阀值修正
%计算误差
e=output_train(:,i)-yn;
E(ii)=E(ii)+sum(abs(e));
%计算权值变化率
dw2=e*Iout;
db2=e';
for j=1:1:midnum
S=1/(1+exp(-I(j)));
FI(j)=S*(1-S);
end
for k=1:1:innum
for j=1:1:midnum
dw1(k,j)=FI(j)*x(k)*(e(1)*w2(j,1)+e(2)*w2(j,2)+e(3)*w2(j,3)+e(4)*w2(j,4));
db1(j)=FI(j)*(e(1)*w2(j,1)+e(2)*w2(j,2)+e(3)*w2(j,3)+e(4)*w2(j,4));
end
end
w1=w1_1+xite*dw1';
b1=b1_1+xite*db1';
w2=w2_1+xite*dw2';
b2=b2_1+xite*db2';
w1_2=w1_1;w1_1=w1;
w2_2=w2_1;w2_1=w2;
b1_2=b1_1;b1_1=b1;
b2_2=b2_1;b2_1=b2;
end
end
%% 语音特征信号分类
inputn_test=mapminmax('apply',input_test,inputps);
for ii=1:1
for i=1:500%1500
%隐含层输出
for j=1:1:midnum
I(j)=inputn_test(:,i)'*w1(j,:)'+b1(j);
Iout(j)=1/(1+exp(-I(j)));
end
fore(:,i)=w2'*Iout'+b2;
end
end
%% 结果分析
%根据网络输出找出数据属于哪类
for i=1:500
output_fore(i)=find(fore(:,i)==max(fore(:,i)));
end
%BP网络预测误差
error=output_fore-output1(n(1501:2000))';
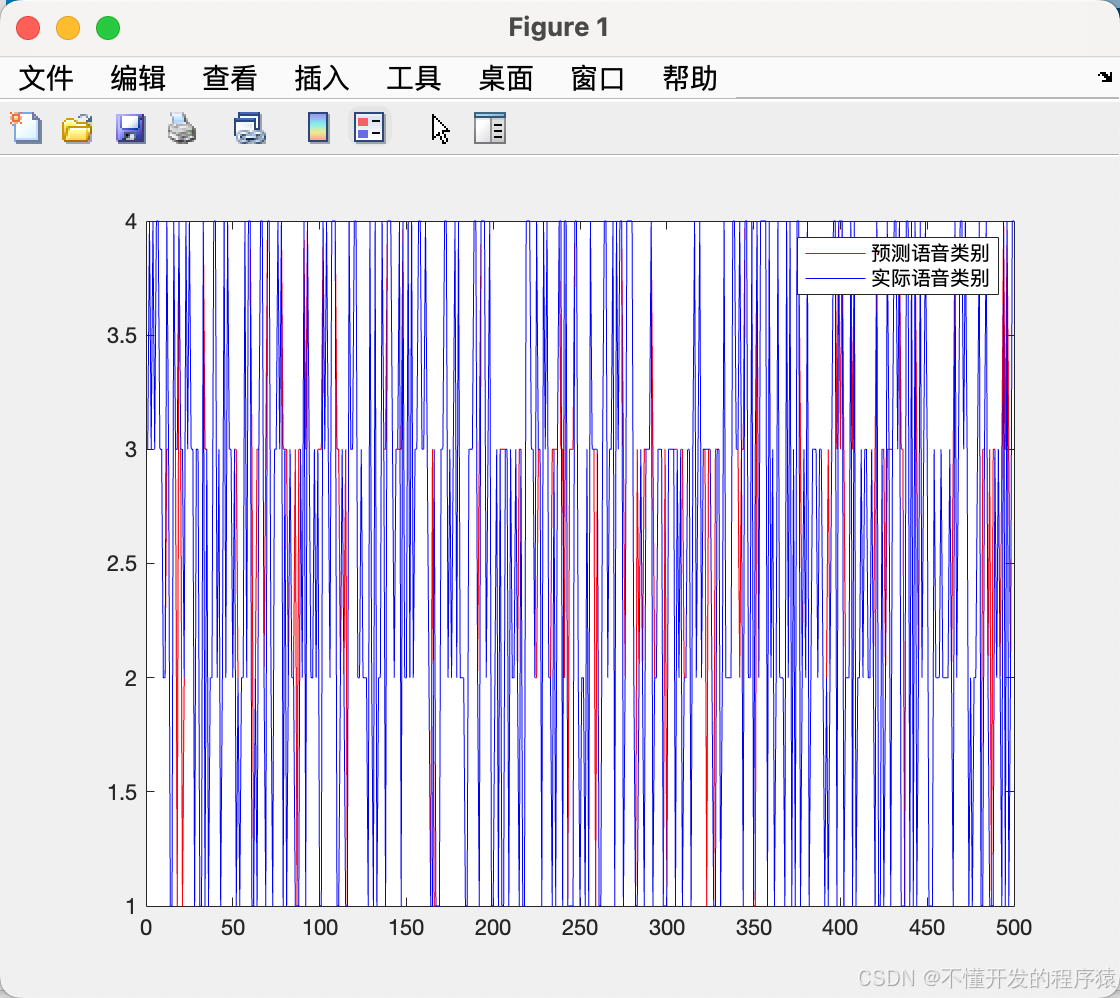
%画出预测语音种类和实际语音种类的分类图
figure(1)
plot(output_fore,'r')
hold on
plot(output1(n(1501:2000))','b')
legend('预测语音类别','实际语音类别')
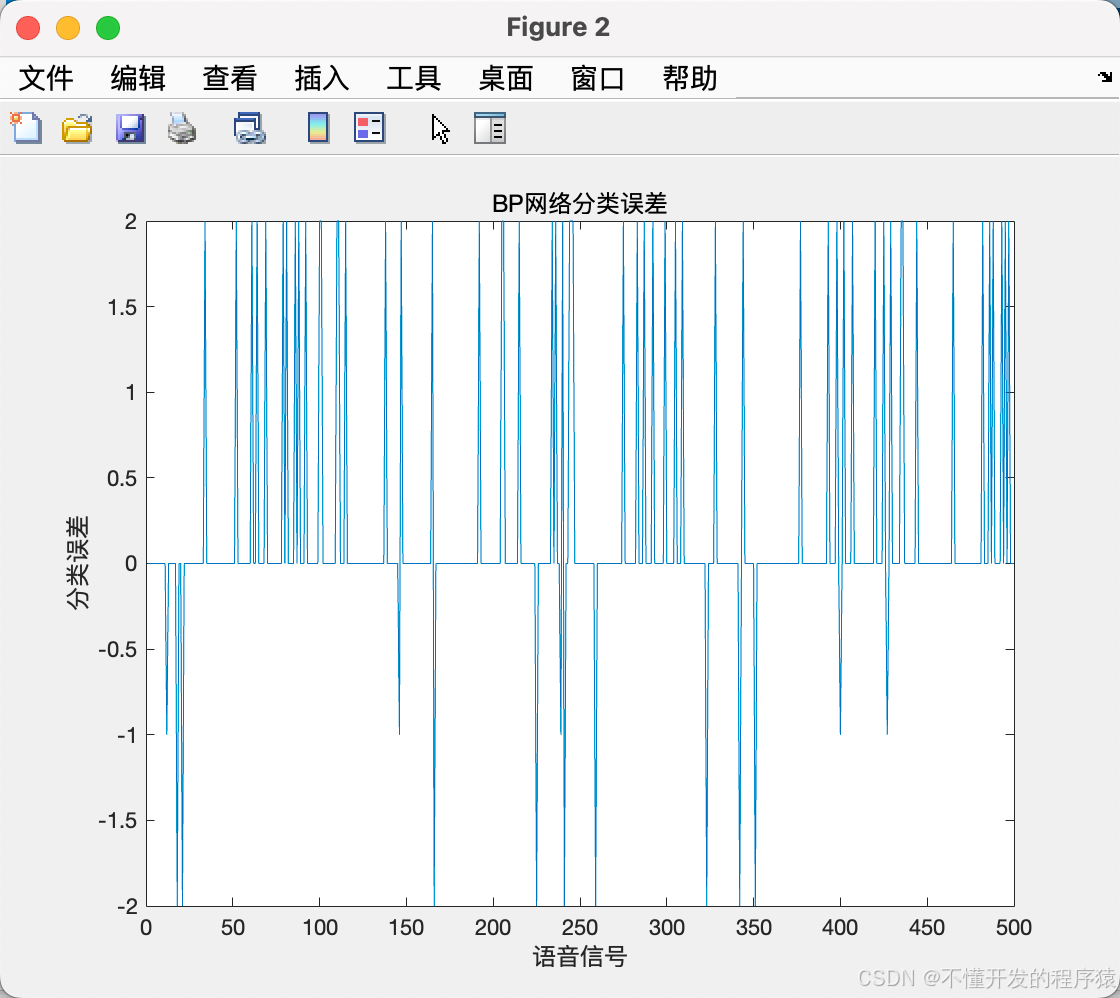
%画出误差图
figure(2)
plot(error)
title('BP网络分类误差','fontsize',12)
xlabel('语音信号','fontsize',12)
ylabel('分类误差','fontsize',12)
%print -dtiff -r600 1-4
k=zeros(1,4);
%找出判断错误的分类属于哪一类
for i=1:500
if error(i)~=0
[b,c]=max(output_test(:,i));
switch c
case 1
k(1)=k(1)+1;
case 2
k(2)=k(2)+1;
case 3
k(3)=k(3)+1;
case 4
k(4)=k(4)+1;
end
end
end
%找出每类的个体和
kk=zeros(1,4);
for i=1:500
[b,c]=max(output_test(:,i));
switch c
case 1
kk(1)=kk(1)+1;
case 2
kk(2)=kk(2)+1;
case 3
kk(3)=kk(3)+1;
case 4
kk(4)=kk(4)+1;
end
end
%正确率
rightridio=(kk-k)./kk
xite =
0.1000
rightridio =
0.5299 1.0000 0.9552 0.9380
>>
4. BP网络的蝴蝶花分类预测
算法步骤:
Step 1,初始化数据,设定各层节点数、学习效率等值;
Step 2,输入层FA输入样品,计算出隐层FB活动;
b(ki)=logsig(aV(:,ki)+Pi(ki))
Step 3,计算出输出层FC活动;
c(kj)=logsig(bW(:,kj)+Tau(kj))
Step 4,网络输出和期望输出相比较,计算出输出层FC的错误;
d=c.(1-c).(ck-c)
Step 5,反传,计算出隐层FB的错误;
e=b.(1-b).(dW’)
Step 6,修改FC层和FB之间的权值wij;
DeltaW(ki,kj)=Alphab(ki)d(kj)+GammaDeltaWOld(ki,kj)
W=W+DeltaW
Step 7,修改FA层和FB之间的权值vhj;
DeltaV(kh,ki)=Beta*a(kh)*e(ki)
V=V+DeltaV
Step 8,修改偏差。
clc % 清屏
clear all; % 删除workplace变量
close all; % 关掉显示图形窗口
format long
% Initial
% parameters for the NN structure
h=4;
i=3;
j=3;
Alpha=0.1;
Beta=0.1;
Gamma=0.85;
Tor=0.0005;
Maxepoch=2000;
Accuracy=0;
Ntrain=115;
Ntest=35;
%assign random values in the range [-1, +1]
V=2*(rand(h,i)-0.5);
W=2*(rand(i,j)-0.5);
Pi=2*(rand(1,i)-0.5);
Tau=2*(rand(1,j)-0.5);
DeltaWOld(i,j)=0; %set the delat of Wij to 0
DeltaVOld(h,i)=0; %set the delat of Vij to 0
DeltaPiOld(i)=0; %set the delat of Pi to 0
DeltaTauOld(j)=0; %set the delat of Tau to 0
% the learning process
Epoch=1;
Error=10;
% load the training set data and test set data
load data.dat
Odesired=data(:,2); % get the desired of output of 150 data sets
% normalize the input data to rang [-1 +1]
datanew=data(:,3:6);
maxv=max(max(datanew));
minv=min(min(datanew));
datanorm=2*((datanew-minv)/(maxv-minv)-0.5);
while Error>Tor
Err(Epoch)=0;
for k=1:Ntrain % k = the index of tranning set
a=datanorm(k,:); % get the input
% set the desired output ck[j]
if data(k,2)==0
ck=[1 0 0];
elseif data(k,2)==1
ck=[0 1 0];
else
ck=[0 0 1];
end;
% calculate the hidden nodes activation
for ki=1:i
b(ki)=logsig(a*V(:,ki)+Pi(ki));
end;
% calculate the output nodes activation
for kj=1:j
c(kj)=logsig(b*W(:,kj)+Tau(kj));
end;
% calculate error in output Layer FC
d=c.*(1-c).*(ck-c);
% calculate error in hidden layer FB
e=b.*(1-b).*(d*W');
% adjust weights Wij between FB and FC
for ki=1:i
for kj=1:j
DeltaW(ki,kj)=Alpha*b(ki)*d(kj)+Gamma*DeltaWOld(ki,kj);
end
end;
W=W+DeltaW;
DeltaWOld=DeltaW;
% adjust weights Vij between FA and FB
for kh=1:h
for ki=1:i
DeltaV(kh,ki)=Beta*a(kh)*e(ki);
end
end;
V=V+DeltaV;
DeltaVold=DeltaV;
% adjust thresholds Pi and Tau
DeltaPi=Beta*e+Gamma*DeltaPiOld;
Pi=Pi+DeltaPi;
DeltaPiold=DeltaPi;
DeltaTau=Alpha*d+Gamma*DeltaTauOld;
Tau=Tau+DeltaTau;
DeltaTauold=DeltaTau;
% the error is the max of d(1),d(2),d(3)
Err(Epoch)=Err(Epoch)+0.5*(d(1)*d(1)+d(2)*d(2)+d(3)*d(3));
end %for k=1:Ntrain
Err(Epoch)=Err(Epoch)/Ntrain;
Error=Err(Epoch);
% the training stops when iterate is too much
if Epoch > Maxepoch
break;
end
Epoch = Epoch +1; % update the iterate number
end
% test data
for k=1:Ntest % k = the index of test set
a=datanorm(Ntrain+k,:); % get the input of test sets
% calculate the hidden nodes activation
for ki=1:i
b(ki)=logsig(a*V(:,ki)+Pi(ki));
end;
% calculate the output of test sets
for kj=1:j
c(kj)=logsig(b*W(:,kj)+Tau(kj));
end;
% transfer the output to one field format
if (c(1)> 0.9)
Otest(k)=0;
elseif (c(2)> 0.9)
Otest(k)=1;
elseif (c(3)> 0.9)
Otest(k)=2;
else
Otest(k)=3;
end;
% calculate the accuracy of test sets
if Otest(k)==Odesired(Ntrain+k)
Accuracy=Accuracy+1;
end;
end; % k=1:Ntest
% plot the error
plot(Err);
% plot the NN output and desired output during test
N=1:Ntest;
figure; plot(N,Otest,'b-',N,Odesired(116:150),'r-');
% display the accuracy
Accuracy = 100*Accuracy/Ntest;
t=['正确率: ' num2str(Accuracy) '%' ];
disp(t);
正确率: 91.4286%
>>
误差图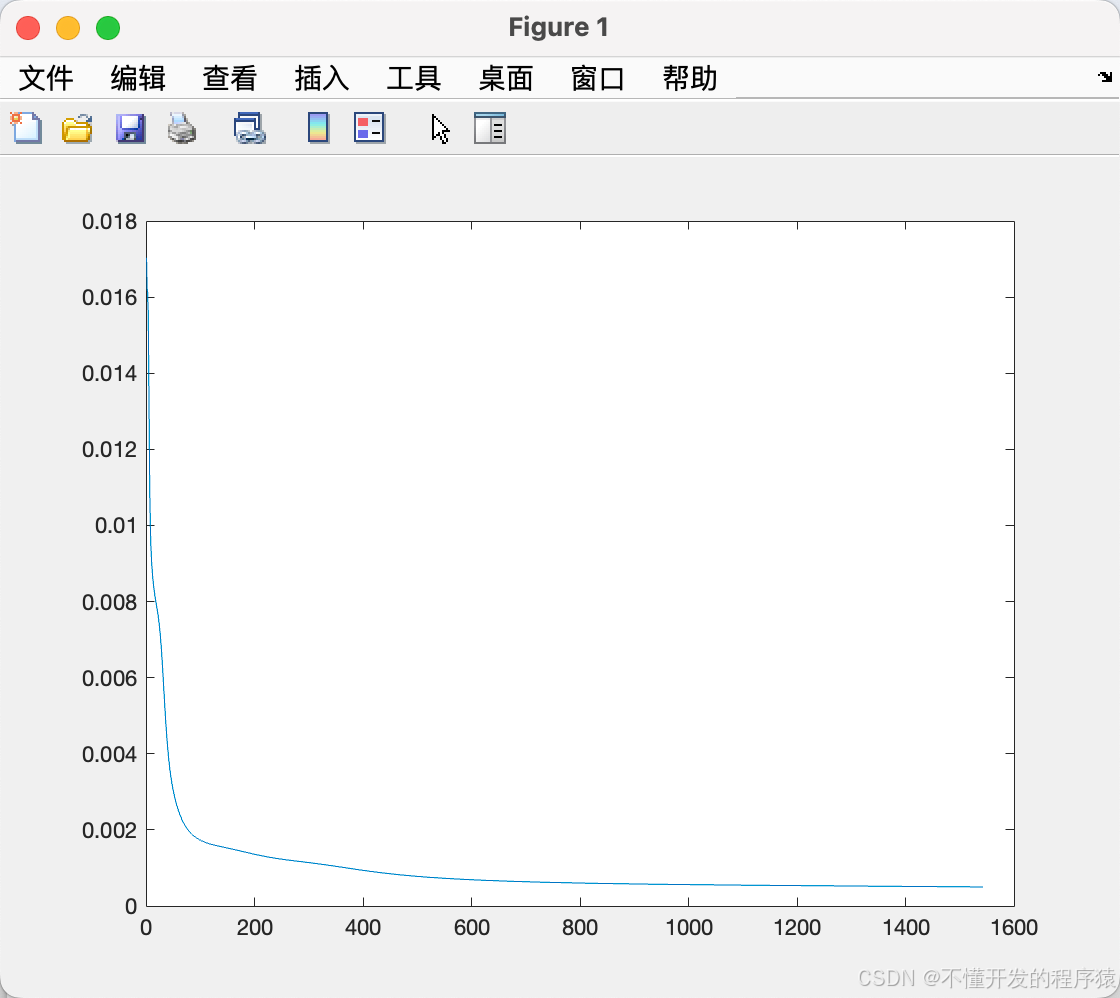
预测值和期望值
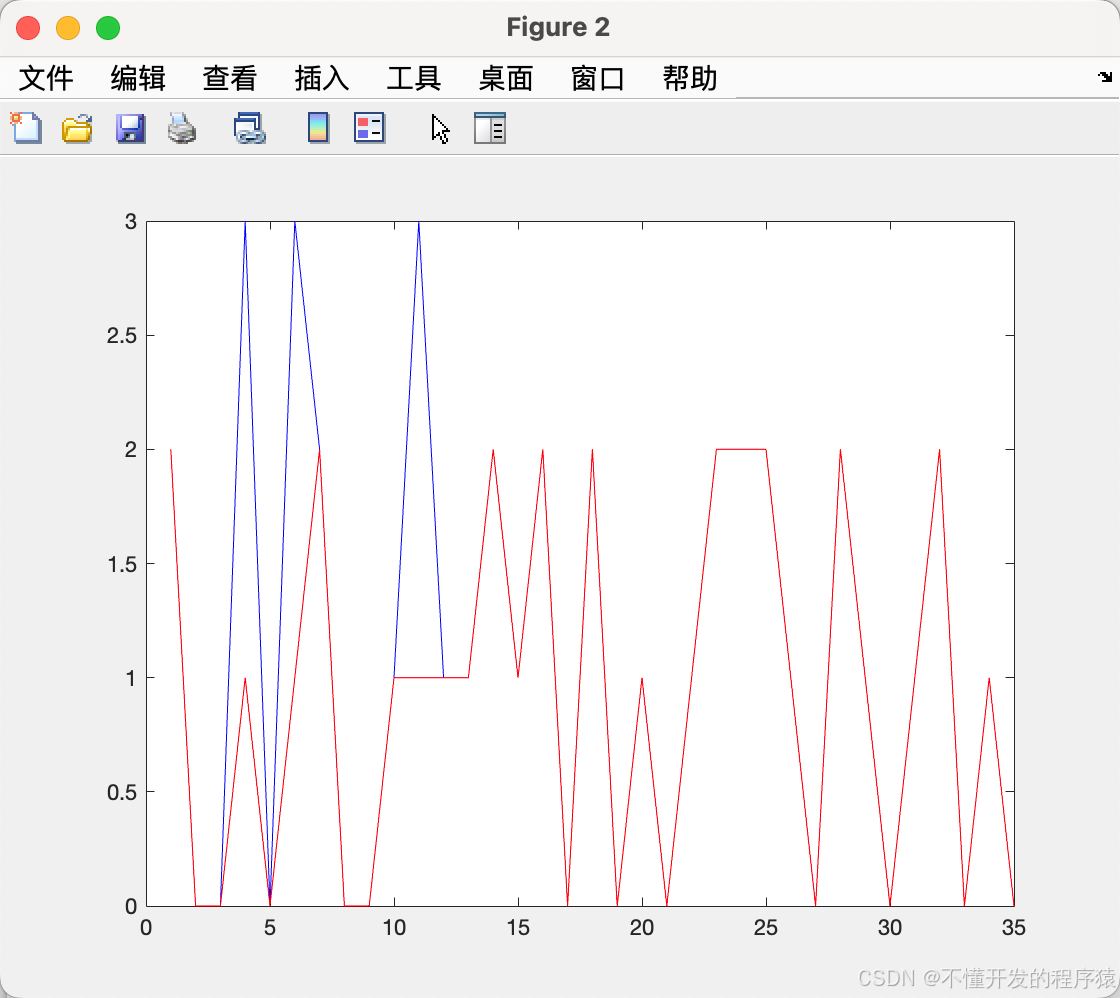
–end–
更多推荐
 已为社区贡献9条内容
已为社区贡献9条内容











所有评论(0)