深度学习理论基础(一)| 机器学习基础
让计算机具有像人一样的学习和思考能力技术的总称。具体来说是从已知数据中获取规律,并利用规律对未知数据进行预测的技术。
目录
一、机器学习基本概念
1. 机器学习定义
让计算机具有像人一样的学习和思考能力技术的总称。具体来说是从已知数据中获取规律,并利用规律对未知数据进行预测的技术。
2. 机器学习分类
- 有监督学习(跟学师评):有老师(环境)的情况下,学生(计算机)从老师(环境)那里获得对错指示、最终答案的学习方法。
- 无监督学习(自学标评):没有老师(环境)的情况下,学生(计算机)自学的过程,一般使用一些既定标准进行评价,或无评价。
- 弱监督学习:仅有少量环境提示(教师反馈)或者少量数据(试题)标签(答案)的情况下,机器(学生)不断进行学习的方法。
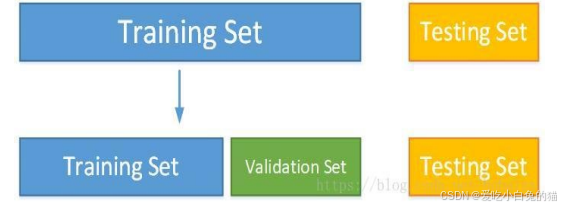
3. 数据集分类
- 训练集:用于模型拟合的数据样本
- 验证集:是模型训练过程中单独留出的样本集,可以用于调整模型的超参数和用于对模型的能力进行初步评估。
- 测试集:用来评估最终模型的泛化能力。但不能作为调参、选择特征等算法相关的选择的依据。
4. 数据集
- 观测样本的集合,具体地,
表示一个包含n饿样本的数据集。其中,
是一个向量,表述数据集的第i个样本,其维度d成为样本空间的维度。
- 向量
的元素成为样本的特征,其取值可以是连续的,也可以是离散的。而从数据集中学出模型的过程,便成为“学习”或“训练”。
5. 误差
- 算法实际预测输出的与样本真实输出之间的差异。
- 模型在训练集上的误差成为“训练误差”。
- 在新样本上的误差成为“泛化误差”。
- 由于我们事先不知道新样本是什么,所以只能尽量最小化训练误差。
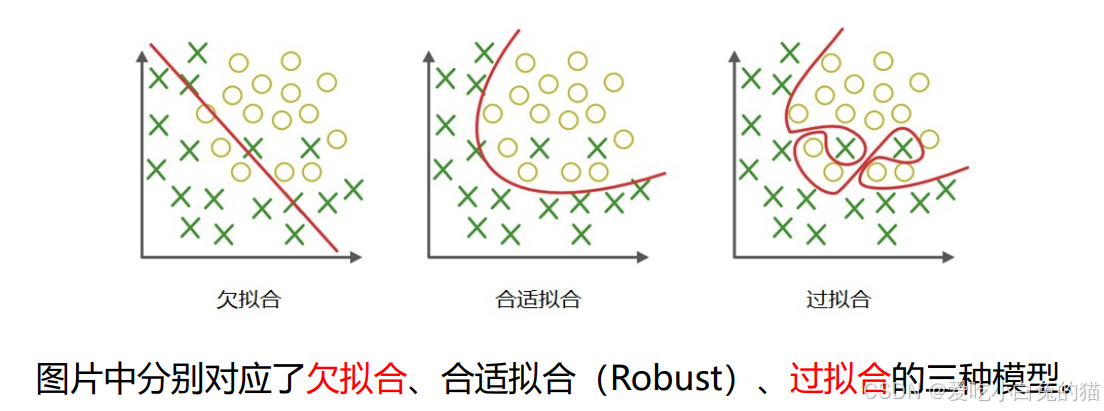
6. 过拟合
- 是指模型能够很好地拟合训练样本,而无法很好地拟合测试样本的现象,从而导致泛化性能下降。
- 为了防止“过拟合”,可以选择减少参数、降低模型复杂度、正则化等。
7. 欠拟合
- 是指模型还没有很好地训练出数据的一般规律,模型拟合程度不高的现象。
- 为防止“欠拟合”,可以选择调整参数、增加迭代深度、换用更加复杂的模型等。
二、机器学习分类
无监督学习:代表任务“聚类”和“降维”
有监督学习:代表任务“分类”和“回归”
1. 无监督学习:数据集没有标记信息(自学)
- 聚类:我们可以使用无监督学习来预测各样本之间的关联度,把关联度大的样本划为同一类,关联度小的样本划为不同类,这就是“聚类”。
- 降维:我们也可以使用无监督学习处理数据,把维度较高、计算复杂的数据,转化为维度低、易处理、且蕴含信息不丢失或较少丢失的数据,这便是“降维”。
2. 监督学习:数据集有标记(答案)
- 数据集通常扩展为
,其中
是
的标记,
是所有标记的集合,称为“标记空间”或“输出空间”。
- 监督学习的任务是训练出一个模型用于预测y的取值,根据
,训练出函数
,使得
。
- 若预测的值是离散值,如年龄,此类学习任务称为“分类”。
- 若预测的值是连续值,如房价,此类学习任务称为“回归”。
三、机器学习算法
1. 监督学习—线性回归
- 线性回归:在样本属性和标签中找到一个线性关系的方法。其目的是根据训练数据找到一个线性模型,使得模型产生的预测值与样本标签的差距最小。若用
表示第k个样本的第i个属性,则线性模型一般形式为:
- 线性回归学习的对象就是权重向量
和偏置向量
。如果用最小均方误差来衡量预测值与样本标签的差距,那么线性回归学习的目标函数可以 表示为:
2. 监督学习—逻辑回归
- 逻辑回归:Logistic回归利用sigmoid函数,将线性回归产生的预测值压缩到0和1之间。此时将y视作样本为正例的可能性,即:
- 注意,逻辑回归本质上属于分类算法。sigmoid函数的表达式为:
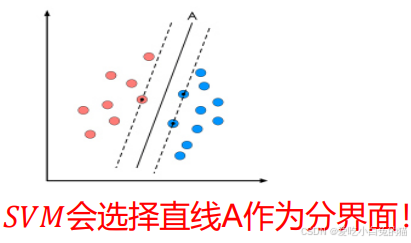
3. 有监督学习算法:SVM
- 支持向量机(SVM)是监督学习中最具有影响力的方法之一,是基于线性判别函数的一种模型。
- SVM的思想非常简单,对于线性可分的数据,能将训练样本划分开的超平面有很多,于是我们寻找“位于两类训练样本正中心的超平面”,即margin最大化。从直观上看,这种划分对训练样本局部扰动的承受性最好。事实上,这种划分的性能表现也较好。
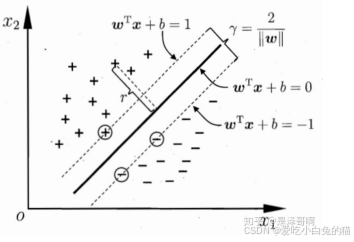
- 对于二类可分的数据集
,
- 每个支持向量到超平面的距离d:
- 通常为方便优化,原问题转化为:
4. 有监督学习算法:决策树
- 决策树(Decision Tree),是一种基于树结构进行决策的机器学习方法,这恰是人类面临决策时一种很自然的处理机制。
- 接下来以一个实例,来介绍决策树中的ID3算法:
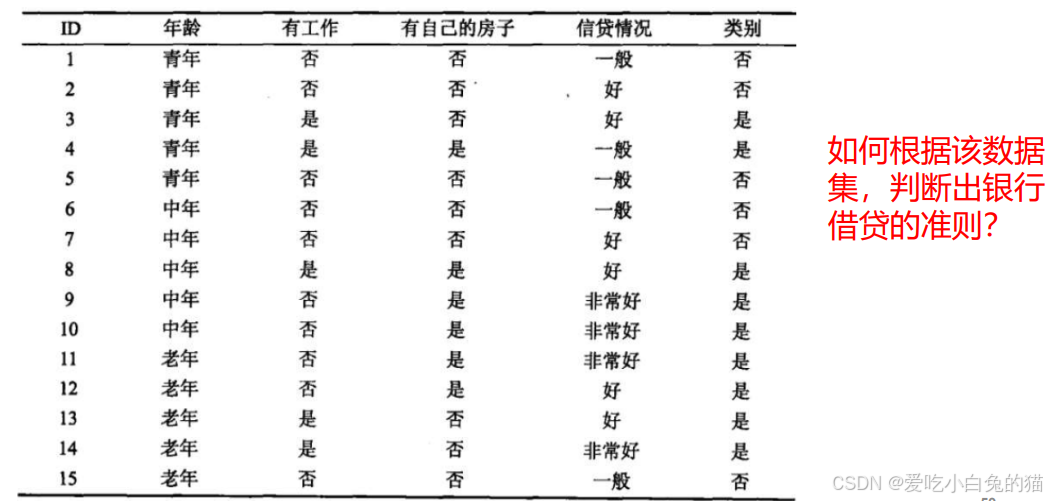
决策树生成过程中,最重要的因素便是根节点的选择,即选择那种特征作为决策因素。ID3算法使用信息增益作准则。
输入:训练数据集D和特征A;
输出:特征A对训练数据集D的信息增益
;
(1)计算数据集的熵
(2)计算特征A对数据集D的条件熵
(3)计算信息增益
第一步,
进一步地,
- 由于特征
(有房子)的信息增益最大,所以选择
作为最优特征。
取值为“是”的情况下,均可贷款,无需再细分,为叶结点;
- 将
取值为“否”的样本提取出来,构成子数据集
。
显然,决策树的生成是一个递归过程,有三种情况会导致递归返回:
- 当前结点包含的样本属于同一类别。
- 当前属性集为空,或所有样本在所有属性取值相同。
- 当前结点包含的集合为空。

5. 有监督学习算法:随即森林
- 随机森林(Random Forest):该算法用随机的方式建立起一棵棵决策树,然后由这些决策树组成一个森林,其中每棵决策树之间没有关联。
- 当有一个新的样本输入时,就让每棵树独立做出判断,按照多数原则(得到票数最多的分类结果)决定该样本的分类结果。
- 这是一种典型的集成学习思想。
无监督学习方法:聚类
- 聚类的目的是“将数据分为多个类别,在同一个类内,对象(实体)之间具有较高的相似性,在不同类内,对象之间具有较大的差异性”。
- 对一批没有类别标签的样本集,按照样本之间的相似程度分类,相似的归为一类,不相似的归为其他类。这种分类成为聚类分析,也称为无监督分类。
K-means聚类
是一个反复迭代的过程,算法分为四个步骤:
1)随机选择数据空间中的K个对象作为初始中心,每个对象代表一个聚类中心;
2)对于样本中的数据对象,根据它们与这些聚类中心的欧氏距离,按距离最近的准则将他们分到距离他们最近的聚类中心(最相似)所对应的类;
3)更新聚类中心:将每个类别中所有对象所对应的均值作为该类别的聚类中心,计算目标函数的值;
4)判断聚类中心和目标函数的值是否发生改变,若不变,则输出结果,若改变,返回2)。
6. 无监督学习-降维
- 降维的目的是“将原始样本数据的维度d降低到一个更小的数m,且尽量使得样本所蕴含信息量损失最小,或还原数据时产生的误差最小”。
- 降维算法具有很多好处:
数据在低维下更容易处理、更容易使用;
相关特征,特别是重要特征更能在数据中明确的显示出来;
如果只有二维或者三维,能够进行可视化展示;
可以去除数据噪声,降低算法开销等。
主成分分析法
假设我们有n个无标签的d维样本
,记为
,我们想寻找一个矩阵
,那么
便是降维后的样本
,我们希望新的样本
具有最大的方差,具体计算步骤如下:
1.计算样本协方差矩阵
;
2.对
进行特征分解;
3.找出
最大的m个特征值
和相应的特征向量
;
4.令
;
5.
即为所求的变换矩阵。
更多推荐
 已为社区贡献2条内容
已为社区贡献2条内容







所有评论(0)