依旧是，简略数学推导

只讲原理

只讲应用

毕竟我们又不是去做一个数学上的创新或者叫算法上的创新

能够将真正经过市场检验过的需求进行满足即可

基本原理，是什么是SVM

向量机的核心目标是对一组数据进行分类处理

先从二分类开始，依旧以识别手写1-9为例

手写数字识别：

• 假设你想教计算机识别手写数字（0-9）。每个数字都是一个图像，可以看作是一个高维空间中的点（每个像素点的亮度作为一个维度）。
• 训练SVM：
  • 收集大量手写数字的图片，每张图片标注了它代表的数字。
  • SVM 会尝试找到一个超平面（在这种情况下，是一个高维空间的决策边界），使数字0和数字1（或任何其他数字）之间的间隔最大化。
  • 这个决策边界就是SVM找到的线性分类器。支持向量是那些最接近这个边界的数字图像。

原理可视化展示

https://www.youtube.com/watch?v=Q7vT0--5VII

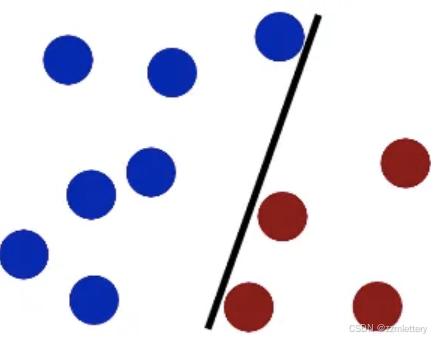
SVM就是试图把棍放在最佳位置，好让在棍的两边有尽可能大的间隙。这个间隙就是球到棍的距离

而有一个大侠出招了，将所有球振起，从空间上选择了一个最好的平面去分割

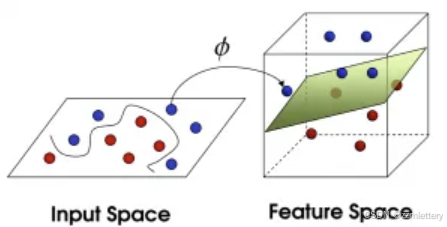
再之后，这些球叫做data，棍子叫做classifier, 找到最大间隙的trick叫做optimization，拍桌子叫做kernelling, 那张纸叫做hyperplane。

想要让数据飞起，我们需要的东西就是核函数(kernel)，用于切分小球的纸，就是超平面

可以看出，问题是从线性可分延伸到线性不可分的

接下来是数学推导（超简略版）

从一个直线函数开始

求出一个决策直线

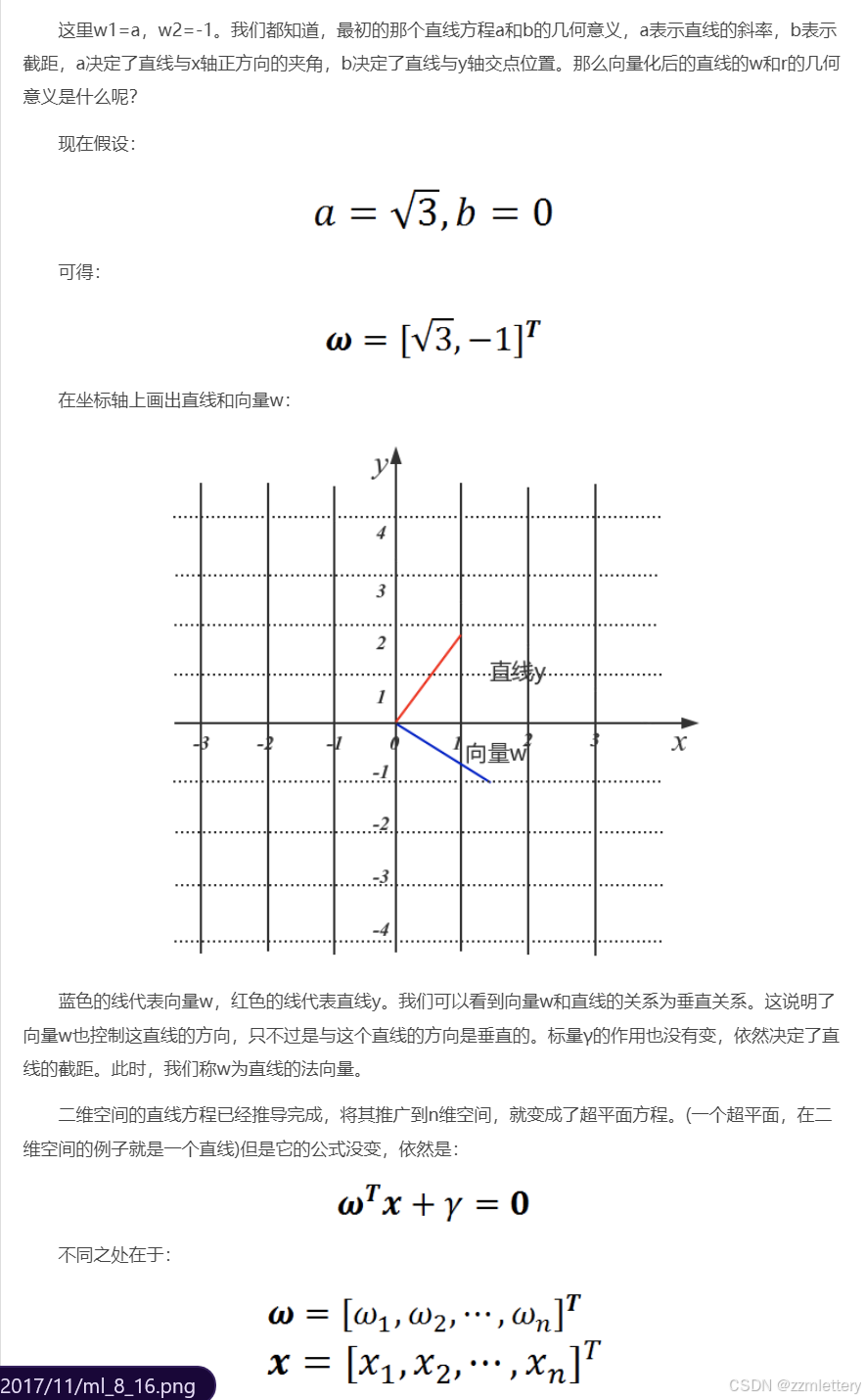
由上面的图像可知，不难理解

二分类一个直线的直线就是它的法向量（垂直目标直线的直线

然后拓展到n维即可

然后是如何评判分类的好坏，因为法向量也可以不止一个吧

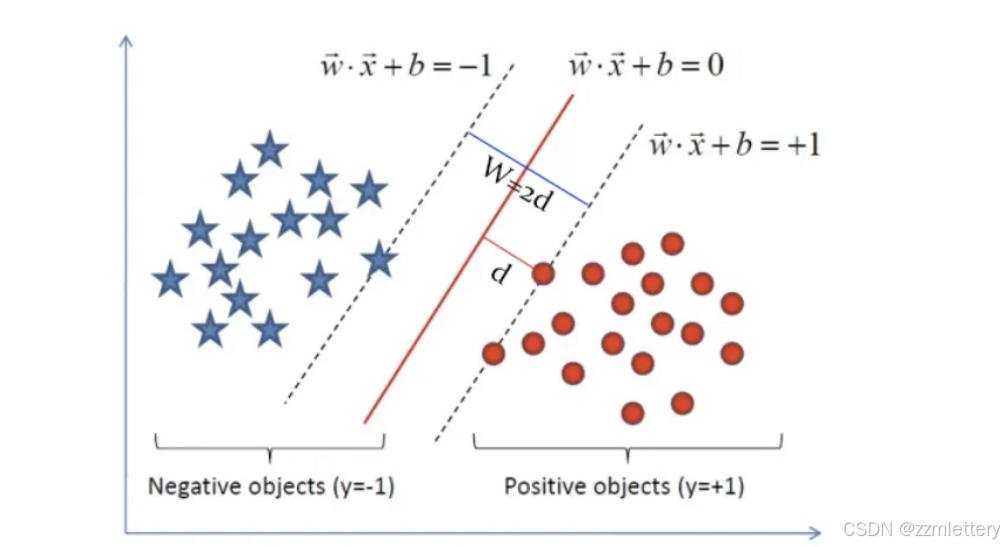
我们要找到能够最好的评分两类数据的线

此时，求解超平面的问题就变成了求解分类间隔W最大化的为题。W的最大化也就是d最大化的。

求最值问题，我们先需要一个约束条件

而它的约束条件是什么，怎么表示，有很多

然后就是转化，求解，验证（省略一万字）

不同的解法中，有一个非常有名的解法

SMO算法求解（也省略一万字）

在结果完全相同的同时，SMO算法的求解时间短很多

接下来，把向量机放到我们前几天的手写识别中，

代码和kNN的实现是差不多的，就是换了个分类器而已

代码都放在github了https://github.com/letteryzzm/Machine-Learning

# -*-coding:utf-8 -*-
import matplotlib.pyplot as plt
import numpy as np
import random
import os


class optStruct:
	"""
	数据结构，维护所有需要操作的值
	Parameters：
		dataMatIn - 数据矩阵
		classLabels - 数据标签
		C - 松弛变量
		toler - 容错率
		kTup - 包含核函数信息的元组,第一个参数存放核函数类别，第二个参数存放必要的核函数需要用到的参数
	"""
	def __init__(self, dataMatIn, classLabels, C, toler, kTup):
		self.X = dataMatIn								#数据矩阵
		self.labelMat = classLabels						#数据标签
		self.C = C 										#松弛变量
		self.tol = toler 								#容错率
		self.m = np.shape(dataMatIn)[0] 				#数据矩阵行数
		self.alphas = np.mat(np.zeros((self.m,1))) 		#根据矩阵行数初始化alpha参数为0	
		self.b = 0 										#初始化b参数为0
		self.eCache = np.mat(np.zeros((self.m,2))) 		#根据矩阵行数初始化虎误差缓存，第一列为是否有效的标志位，第二列为实际的误差E的值。
		self.K = np.mat(np.zeros((self.m,self.m)))		#初始化核K
		for i in range(self.m):							#计算所有数据的核K
			self.K[:,i] = kernelTrans(self.X, self.X[i,:], kTup)

def kernelTrans(X, A, kTup): 
	"""
	通过核函数将数据转换更高维的空间
	Parameters：
		X - 数据矩阵
		A - 单个数据的向量
		kTup - 包含核函数信息的元组
	Returns:
	    K - 计算的核K
	"""
	m,n = np.shape(X)
	K = np.mat(np.zeros((m,1)))
	if kTup[0] == 'lin': K = X * A.T   					#线性核函数,只进行内积。
	elif kTup[0] == 'rbf': 								#高斯核函数,根据高斯核函数公式进行计算
		for j in range(m):
			deltaRow = X[j,:] - A
			K[j] = deltaRow*deltaRow.T
		K = np.exp(K/(-1*kTup[1]**2)) 					#计算高斯核K
	else: raise NameError('核函数无法识别')
	return K 											#返回计算的核K

def loadDataSet(fileName):
	"""
	读取数据
	Parameters:
	    fileName - 文件名
	Returns:
	    dataMat - 数据矩阵
	    labelMat - 数据标签
	"""
	dataMat = []; labelMat = []
	fr = open(fileName)
	for line in fr.readlines():                                     #逐行读取，滤除空格等
		lineArr = line.strip().split('\t')
		dataMat.append([float(lineArr[0]), float(lineArr[1])])      #添加数据
		labelMat.append(float(lineArr[2]))                          #添加标签
	return dataMat,labelMat

def calcEk(oS, k):
	"""
	计算误差
	Parameters：
		oS - 数据结构
		k - 标号为k的数据
	Returns:
	    Ek - 标号为k的数据误差
	"""
	fXk = float(np.multiply(oS.alphas,oS.labelMat).T*oS.K[:,k] + oS.b)
	Ek = fXk - float(oS.labelMat[k])
	return Ek

def selectJrand(i, m):
	"""
	函数说明:随机选择alpha_j的索引值

	Parameters:
	    i - alpha_i的索引值
	    m - alpha参数个数
	Returns:
	    j - alpha_j的索引值
	"""
	j = i                                 #选择一个不等于i的j
	while (j == i):
		j = int(random.uniform(0, m))
	return j

def selectJ(i, oS, Ei):
	"""
	内循环启发方式2
	Parameters：
		i - 标号为i的数据的索引值
		oS - 数据结构
		Ei - 标号为i的数据误差
	Returns:
	    j, maxK - 标号为j或maxK的数据的索引值
	    Ej - 标号为j的数据误差
	"""
	maxK = -1; maxDeltaE = 0; Ej = 0 						#初始化
	oS.eCache[i] = [1,Ei]  									#根据Ei更新误差缓存
	validEcacheList = np.nonzero(oS.eCache[:,0].A)[0]		#返回误差不为0的数据的索引值
	if (len(validEcacheList)) > 1:							#有不为0的误差
		for k in validEcacheList:   						#遍历,找到最大的Ek
			if k == i: continue 							#不计算i,浪费时间
			Ek = calcEk(oS, k)								#计算Ek
			deltaE = abs(Ei - Ek)							#计算|Ei-Ek|
			if (deltaE > maxDeltaE):						#找到maxDeltaE
				maxK = k; maxDeltaE = deltaE; Ej = Ek
		return maxK, Ej										#返回maxK,Ej
	else:   												#没有不为0的误差
		j = selectJrand(i, oS.m)							#随机选择alpha_j的索引值
		Ej = calcEk(oS, j)									#计算Ej
	return j, Ej 											#j,Ej

def updateEk(oS, k):
	"""
	计算Ek,并更新误差缓存
	Parameters：
		oS - 数据结构
		k - 标号为k的数据的索引值
	Returns:
		无
	"""
	Ek = calcEk(oS, k)										#计算Ek
	oS.eCache[k] = [1,Ek]									#更新误差缓存


def clipAlpha(aj,H,L):
	"""
	修剪alpha_j
	Parameters:
	    aj - alpha_j的值
	    H - alpha上限
	    L - alpha下限
	Returns:
	    aj - 修剪后的alpah_j的值
	"""
	if aj > H: 
		aj = H
	if L > aj:
		aj = L
	return aj

def innerL(i, oS):
	"""
	优化的SMO算法
	Parameters：
		i - 标号为i的数据的索引值
		oS - 数据结构
	Returns:
		1 - 有任意一对alpha值发生变化
		0 - 没有任意一对alpha值发生变化或变化太小
	"""
	#步骤1：计算误差Ei
	Ei = calcEk(oS, i)
	#优化alpha,设定一定的容错率。
	if ((oS.labelMat[i] * Ei < -oS.tol) and (oS.alphas[i] < oS.C)) or ((oS.labelMat[i] * Ei > oS.tol) and (oS.alphas[i] > 0)):
		#使用内循环启发方式2选择alpha_j,并计算Ej
		j,Ej = selectJ(i, oS, Ei)
		#保存更新前的aplpha值，使用深拷贝
		alphaIold = oS.alphas[i].copy(); alphaJold = oS.alphas[j].copy();
		#步骤2：计算上下界L和H
		if (oS.labelMat[i] != oS.labelMat[j]):
			L = max(0, oS.alphas[j] - oS.alphas[i])
			H = min(oS.C, oS.C + oS.alphas[j] - oS.alphas[i])
		else:
			L = max(0, oS.alphas[j] + oS.alphas[i] - oS.C)
			H = min(oS.C, oS.alphas[j] + oS.alphas[i])
		if L == H: 
			print("L==H")
			return 0
		#步骤3：计算eta
		eta = 2.0 * oS.K[i,j] - oS.K[i,i] - oS.K[j,j]
		if eta >= 0: 
			print("eta>=0")
			return 0
		#步骤4：更新alpha_j
		oS.alphas[j] -= oS.labelMat[j] * (Ei - Ej)/eta
		#步骤5：修剪alpha_j
		oS.alphas[j] = clipAlpha(oS.alphas[j],H,L)
		#更新Ej至误差缓存
		updateEk(oS, j)
		if (abs(oS.alphas[j] - alphaJold) < 0.00001): 
			print("alpha_j变化太小")
			return 0
		#步骤6：更新alpha_i
		oS.alphas[i] += oS.labelMat[j]*oS.labelMat[i]*(alphaJold - oS.alphas[j])
		#更新Ei至误差缓存
		updateEk(oS, i)
		#步骤7：更新b_1和b_2
		b1 = oS.b - Ei- oS.labelMat[i]*(oS.alphas[i]-alphaIold)*oS.K[i,i] - oS.labelMat[j]*(oS.alphas[j]-alphaJold)*oS.K[i,j]
		b2 = oS.b - Ej- oS.labelMat[i]*(oS.alphas[i]-alphaIold)*oS.K[i,j]- oS.labelMat[j]*(oS.alphas[j]-alphaJold)*oS.K[j,j]
		#步骤8：根据b_1和b_2更新b
		if (0 < oS.alphas[i]) and (oS.C > oS.alphas[i]): oS.b = b1
		elif (0 < oS.alphas[j]) and (oS.C > oS.alphas[j]): oS.b = b2
		else: oS.b = (b1 + b2)/2.0
		return 1
	else: 
		return 0

def smoP(dataMatIn, classLabels, C, toler, maxIter, kTup = ('lin',0)):
	"""
	完整的线性SMO算法
	Parameters：
		dataMatIn - 数据矩阵
		classLabels - 数据标签
		C - 松弛变量
		toler - 容错率
		maxIter - 最大迭代次数
		kTup - 包含核函数信息的元组
	Returns:
		oS.b - SMO算法计算的b
		oS.alphas - SMO算法计算的alphas
	"""
	oS = optStruct(np.mat(dataMatIn), np.mat(classLabels).transpose(), C, toler, kTup)				#初始化数据结构
	iter = 0 																						#初始化当前迭代次数
	entireSet = True; alphaPairsChanged = 0
	while (iter < maxIter) and ((alphaPairsChanged > 0) or (entireSet)):							#遍历整个数据集都alpha也没有更新或者超过最大迭代次数,则退出循环
		alphaPairsChanged = 0
		if entireSet:																				#遍历整个数据集   						
			for i in range(oS.m):        
				alphaPairsChanged += innerL(i,oS)													#使用优化的SMO算法
				print("全样本遍历:第%d次迭代 样本:%d, alpha优化次数:%d" % (iter,i,alphaPairsChanged))
			iter += 1
		else: 																						#遍历非边界值
			nonBoundIs = np.nonzero((oS.alphas.A > 0) * (oS.alphas.A < C))[0]						#遍历不在边界0和C的alpha
			for i in nonBoundIs:
				alphaPairsChanged += innerL(i,oS)
				print("非边界遍历:第%d次迭代 样本:%d, alpha优化次数:%d" % (iter,i,alphaPairsChanged))
			iter += 1
		if entireSet:																				#遍历一次后改为非边界遍历
			entireSet = False
		elif (alphaPairsChanged == 0):																#如果alpha没有更新,计算全样本遍历 
			entireSet = True  
		print("迭代次数: %d" % iter)
	return oS.b,oS.alphas 																			#返回SMO算法计算的b和alphas


def img2vector(filename):
	"""
	将32x32的二进制图像转换为1x1024向量。
	Parameters:
		filename - 文件名
	Returns:
		returnVect - 返回的二进制图像的1x1024向量
	"""
	returnVect = np.zeros((1,1024))
	fr = open(filename)
	for i in range(32):
		lineStr = fr.readline()
		for j in range(32):
			returnVect[0,32*i+j] = int(lineStr[j])
	return returnVect

def loadImages(dirName):
	"""
	加载图片
	Parameters:
		dirName - 文件夹的名字
	Returns:
	    trainingMat - 数据矩阵
	    hwLabels - 数据标签
	"""
	from os import listdir
	hwLabels = []
	trainingFileList = listdir(dirName)           
	m = len(trainingFileList)
	trainingMat = np.zeros((m,1024))
	for i in range(m):
		fileNameStr = trainingFileList[i]
		fileStr = fileNameStr.split('.')[0]     
		classNumStr = int(fileStr.split('_')[0])
		if classNumStr == 9: hwLabels.append(-1)
		else: hwLabels.append(1)
		trainingMat[i,:] = img2vector('%s/%s' % (dirName, fileNameStr))
	return trainingMat, hwLabels    

def testDigits(kTup=('rbf', 10)):
	"""
	测试函数
	Parameters:
		kTup - 包含核函数信息的元组
	Returns:
	    无
	"""
	training_path = r'F:\AI\machie_learning\Machine-Learning-lettery\kNN\3.数字识别\trainingDigits'
	test_path = r'F:\AI\machie_learning\Machine-Learning-lettery\kNN\3.数字识别\testDigits'  # 假设测试数据在同一个目录下

	dataArr, labelArr = loadImages(training_path)
	b, alphas = smoP(dataArr, labelArr, 200, 0.0001, 10, kTup)
	datMat = np.mat(dataArr); labelMat = np.mat(labelArr).transpose()
	svInd = np.nonzero(alphas.A>0)[0]
	sVs=datMat[svInd] 
	labelSV = labelMat[svInd];
	print("支持向量个数:%d" % np.shape(sVs)[0])
	m,n = np.shape(datMat)
	errorCount = 0
	for i in range(m):
		kernelEval = kernelTrans(sVs,datMat[i,:],kTup)
		predict=kernelEval.T * np.multiply(labelSV,alphas[svInd]) + b
		if np.sign(predict) != np.sign(labelArr[i]): errorCount += 1
	print("训练集错误率: %.2f%%" % (float(errorCount)/m))

    # 使用绝对路径加载测试数据
	dataArr, labelArr = loadImages(test_path)
	errorCount = 0
	datMat = np.mat(dataArr); labelMat = np.mat(labelArr).transpose()
	m,n = np.shape(datMat)
	for i in range(m):
		kernelEval = kernelTrans(sVs,datMat[i,:],kTup)
		predict=kernelEval.T * np.multiply(labelSV,alphas[svInd]) + b
		if np.sign(predict) != np.sign(labelArr[i]): errorCount += 1    
	print("测试集错误率: %.2f%%" % (float(errorCount)/m))

if __name__ == '__main__':
    testDigits()