基于Hopfield神经网络的TSP问题求解（TSP：Traveling Salesman Problem，即旅行商问题）

Hopfield神经网络模型是一种循环神经网络，从输出到输入有反馈连接。在输入的激励下，会产生不断的状态变化。对于一个Hopfield网络来说，关键是在于确定它在稳定条件下的权系数。反馈网络有稳定的，也有不稳定的。对于Hopfield网络来说，如何判别其稳定性也是需要确定的。连续型Hopfield网络结构图如图所示。

不懂开发的程序猿

731人浏览 · 2025-01-02 11:08:48

不懂开发的程序猿 · 2025-01-02 11:08:48 发布

⚠申明：未经许可，禁止以任何形式转载，若要引用，请标注链接地址。全文共计6280字，阅读大概需要10分钟
🌈更多学习内容，欢迎👏关注👀【文末】我的个人微信公众号：不懂开发的程序猿

❗❗❗知识付费，🈲止白嫖，有需要请后台私信或【文末】个人微信公众号联系我

1. Hopfield神经网络

Hopfield神经网络模型是一种循环神经网络，从输出到输入有反馈连接。在输入的激励下，会产生不断的状态变化。
对于一个Hopfield网络来说，关键是在于确定它在稳定条件下的权系数。
反馈网络有稳定的，也有不稳定的。对于Hopfield网络来说，如何判别其稳定性也是需要确定的。连续型Hopfield网络结构图如图所示。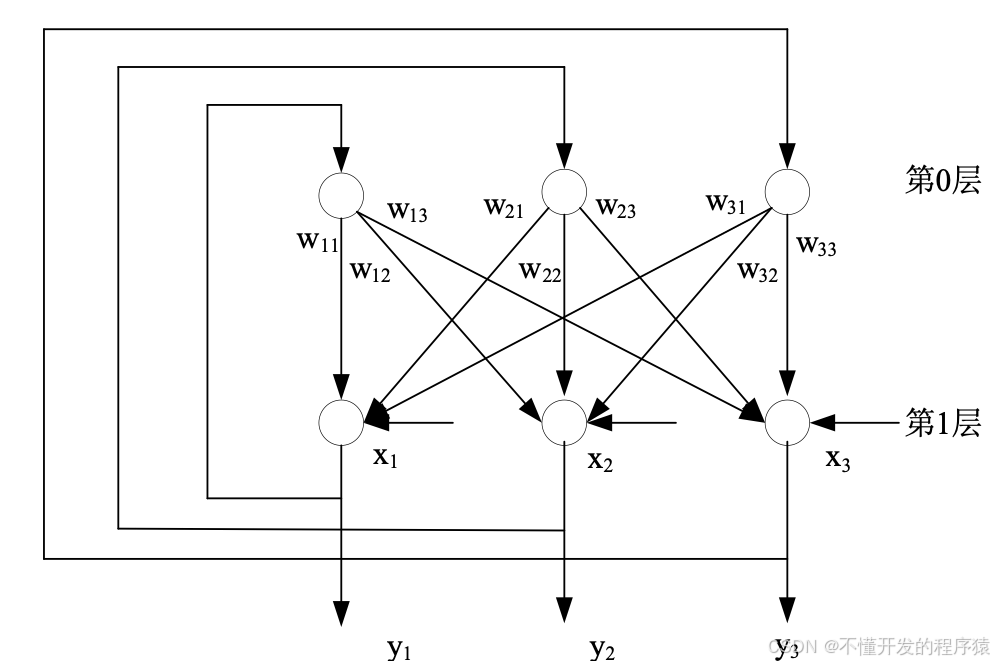
在这里插入图片描述

1.1 离散Hopfield网络

离散Hopfield神经网络简称DHNN。神经元的输出只取1和0，分别表示神经元处于激活和抑制状态。对于二值神经元，它的计算公式如下：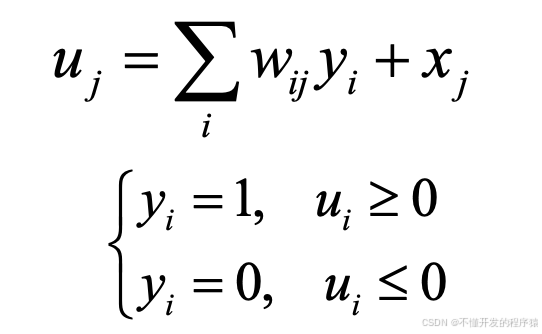
在这里插入图片描述
一个DHNN的网络状态是输出神经元信息的集合。对于一个输出层是 n个神经元的网络，其t 时刻的状态为一个 n 维向量：

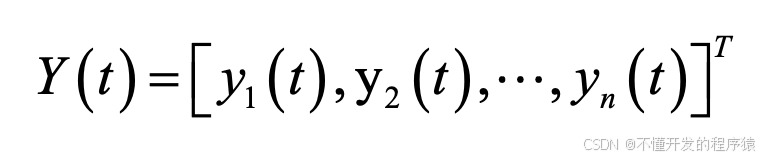
在这里插入图片描述

离散Hopfield网络稳定的充分条件：
（1）权系数矩阵 W 是对称矩阵，并且对角线元素为0。
（2）无自反馈的权系数对称Hopfield网络是稳定的。

离散型Hopfield网络结构图如图所示。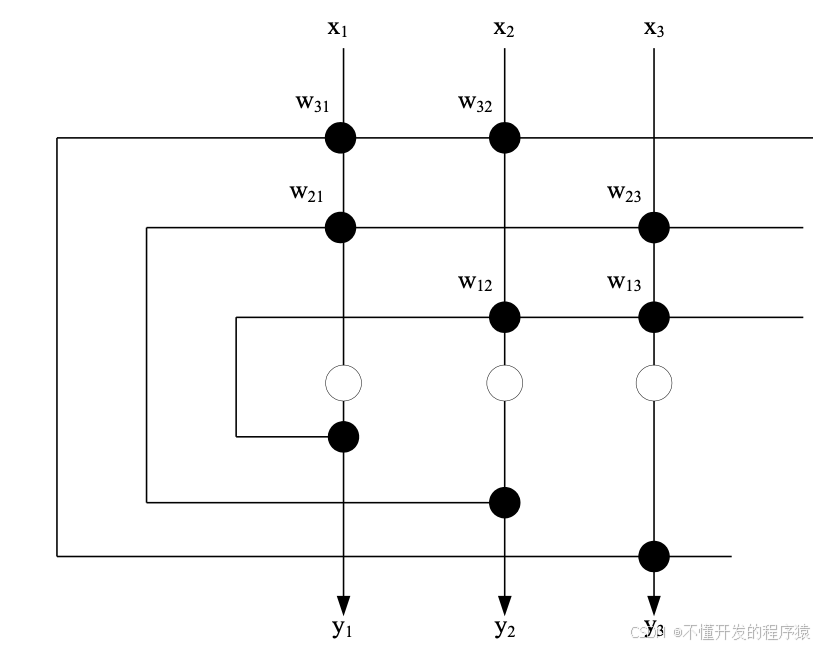
在这里插入图片描述

1.2 连续Hopfield网络

连续Hopfield神经网络简称CHNN。拓扑结构和DHNN的结构相同。不同之处在于其函数g不是阶跃函数，而是S形的连续函数。一般取：
$g(u)=\frac{1}{1+e^u}$

连续Hopfield神经网络反馈闭环结构图如图所示。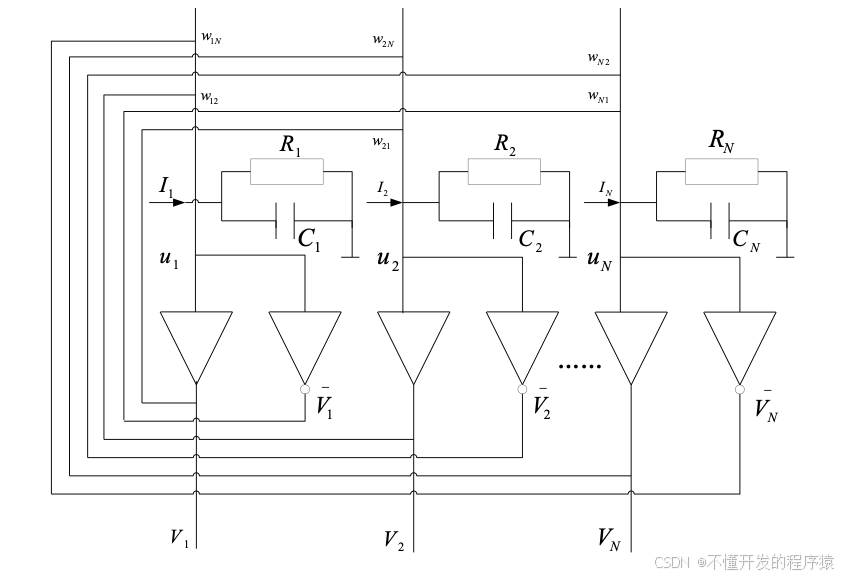
在这里插入图片描述

和离散hopfield网络相比，连续hopfield网络反馈闭环结构的传递函数不同。连续型Hopfield网络（CHNN）是由一些简单的电子线路连接起来实现的。CHNN模拟反馈图如图所示。

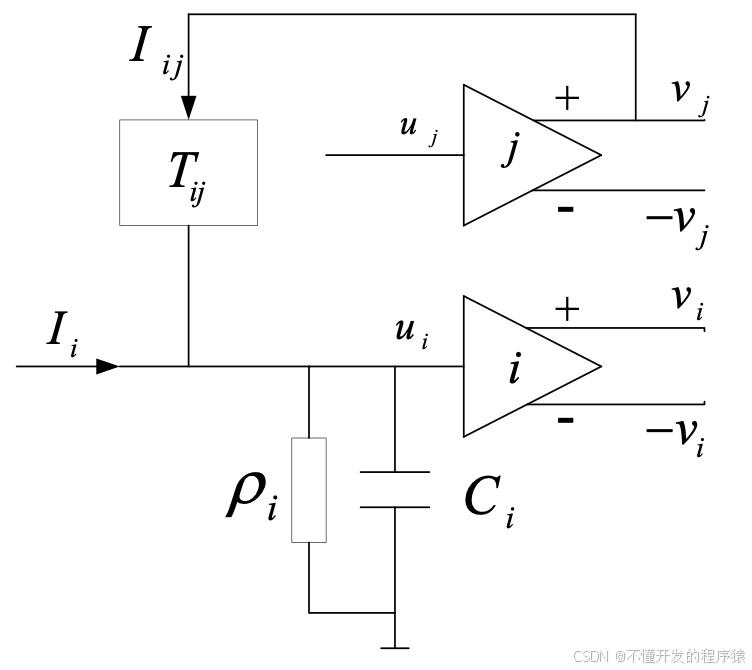
在这里插入图片描述

CHNN用非线性微分方程描述，网络的稳定性通过构造其能量函数（又称李雅谱诺夫函数），并用李雅谱诺夫第二稳定性定理进行判断。
说明：
（1）李雅谱诺夫函数并不唯一；
（2）若找不到网络的李雅谱诺夫函数，不能证明网络不稳定；
（3）目前没有统一的找李雅谱诺夫函数的方法；
（4）用能量函数的方法研究网络的稳定性，在数学上欠严谨。
如果把一个最优化问题的目标函数转换成网络的能量函数，把问题的变量对应于网络的状态，那么Hopfield神经网络就能够用于解决优化组合问题。
应用Hopfield神经网络来解决优化计算问题的一般步骤为：
（1）分析问题：网络输出与问题的解相对应；
（2）构造网络能量函数：使其最小值对应问题最佳解；
（3）设计网络结构：由能量函数和网络稳定条件设计网络参数，得到动力学方程；
（4）MATLAB软件模拟。

2. 基于CHNN的TSP求解

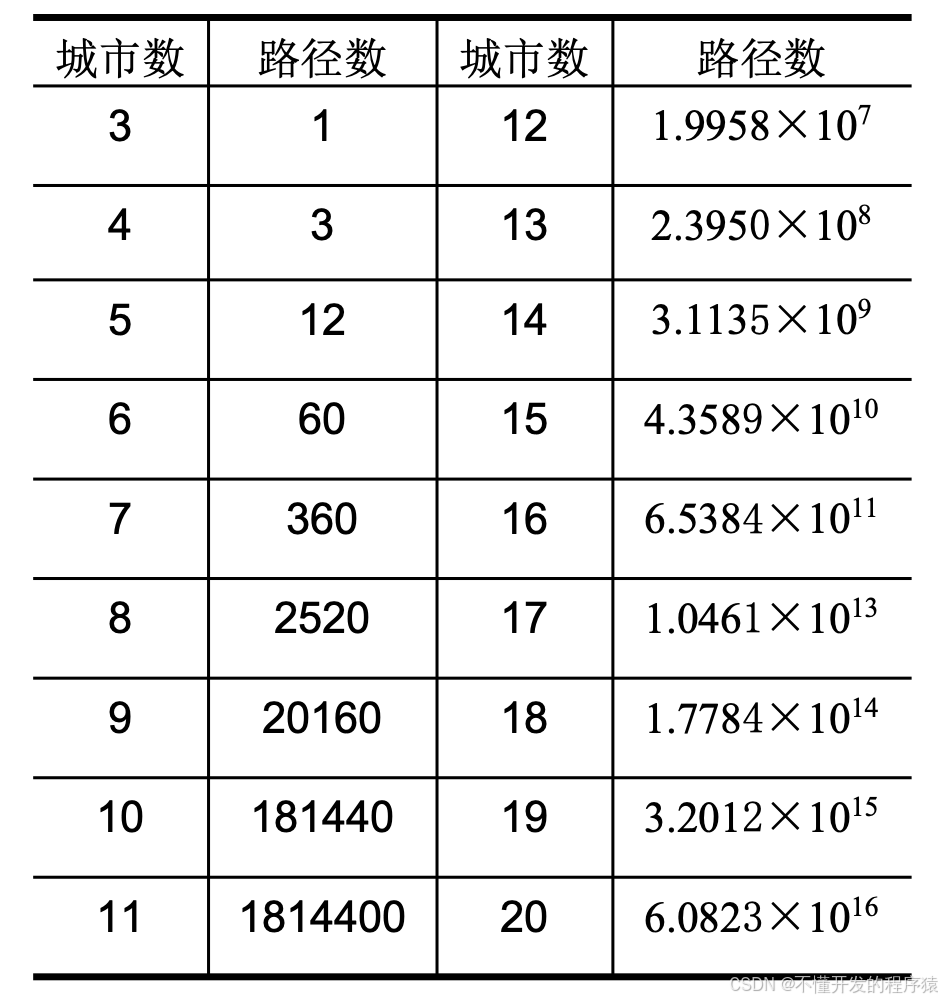
在这里插入图片描述

城市链接关系

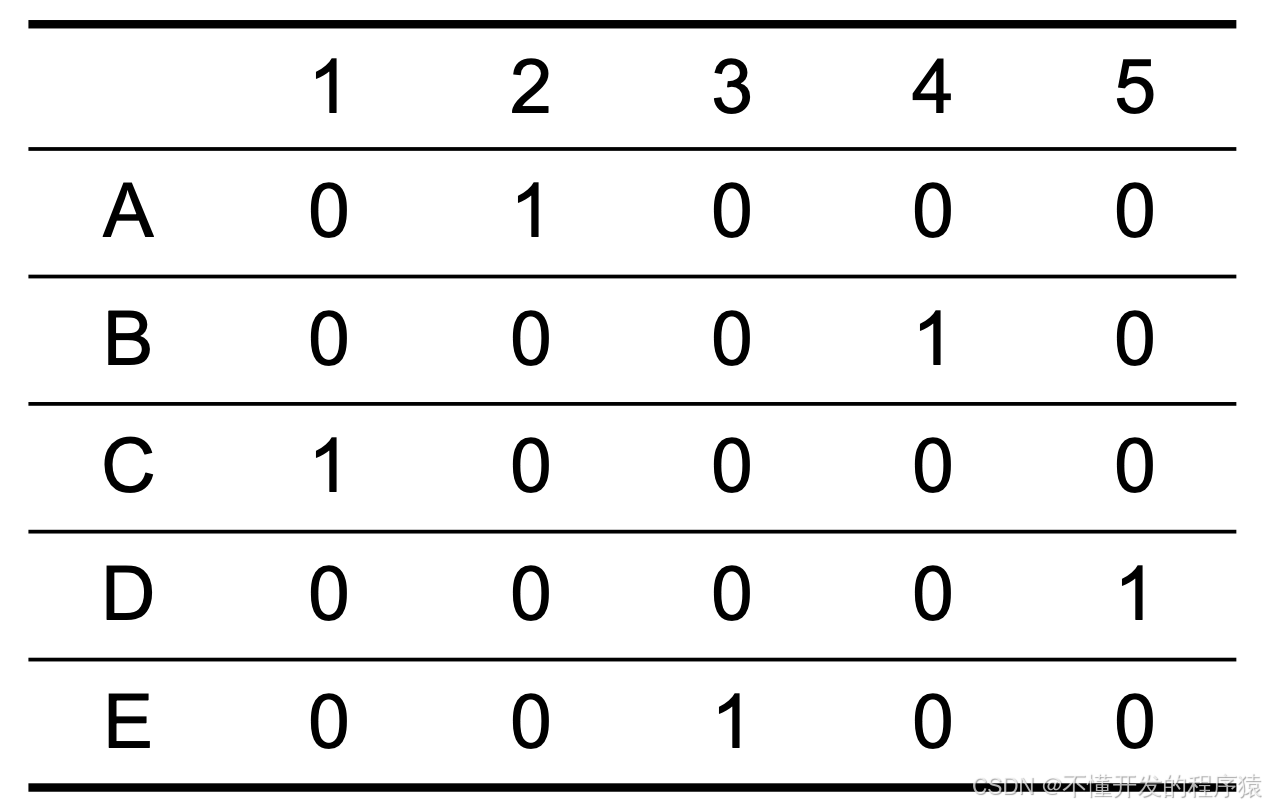
在这里插入图片描述

2.1 算法模型的具体步骤

在这里插入图片描述

2.2 连续Hopfield神经网络求解旅行商问题优化计算

%% 连续Hopfield神经网络的优化—旅行商问题优化计算
% function main
%% 清空环境变量、定义全局变量
clc % 清屏
clear all; % 删除workplace变量
close all; % 关掉显示图形窗口
global A D
%% 导入城市位置
load city_location
%% 计算相互城市间距离
distance=dist(citys,citys');
%% 初始化网络
N=size(citys,1);
A=200;
D=100;
U0=0.1;
step=0.0001;
delta=2*rand(N,N)-1;
U=U0*log(N-1)+delta;
V=(1+tansig(U/U0))/2;
iter_num=10000;
E=zeros(1,iter_num);
%% 寻优迭代
for k=1:iter_num  
    % 动态方程计算
    dU=diff_u(V,distance);
    % 输入神经元状态更新
    U=U+dU*step;
    % 输出神经元状态更新
    V=(1+tansig(U/U0))/2;
    % 能量函数计算
    e=Energy(V,distance);
    E(k)=e;  
end
 %% 判断路径有效性
[rows,cols]=size(V);
V1=zeros(rows,cols);
[V_max,V_ind]=max(V);
for j=1:cols
    V1(V_ind(j),j)=1;
end
C=sum(V1,1);
R=sum(V1,2);
flag=isequal(C,ones(1,N)) & isequal(R',ones(1,N));
%% 结果显示
if flag==1
   % 计算初始路径长度
   sort_rand=randperm(N);
   citys_rand=citys(sort_rand,:);
   Length_init=dist(citys_rand(1,:),citys_rand(end,:)');
   for i=2:size(citys_rand,1)
       Length_init=Length_init+dist(citys_rand(i-1,:),citys_rand(i,:)');
   end
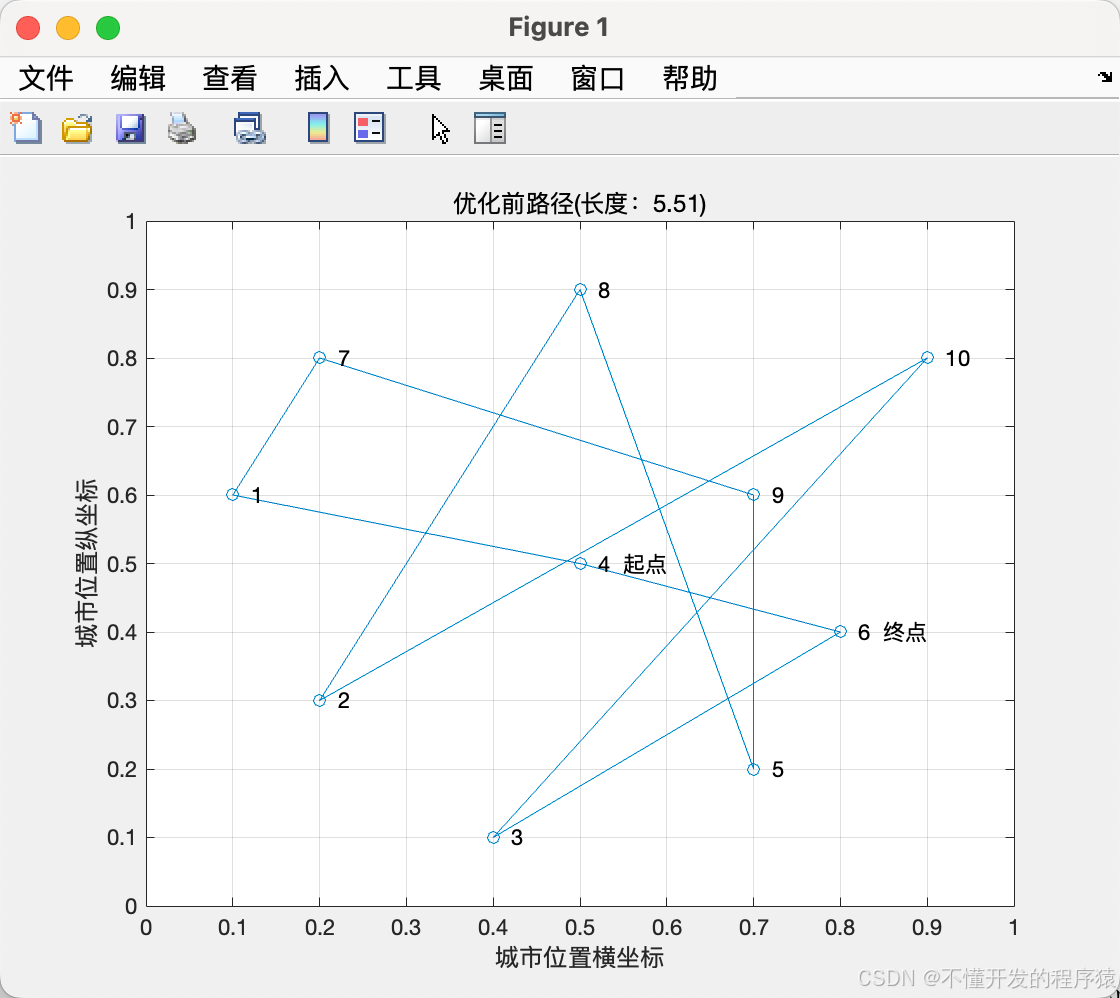
   % 绘制初始路径
   figure(1)
   plot([citys_rand(:,1);citys_rand(1,1)],[citys_rand(:,2);citys_rand(1,2)],'o-')
   for i=1:length(citys)
       text(citys(i,1),citys(i,2),['   ' num2str(i)])
   end
   text(citys_rand(1,1),citys_rand(1,2),['       起点' ])
   text(citys_rand(end,1),citys_rand(end,2),['       终点' ])
   title(['优化前路径(长度：' num2str(Length_init) ')'])
   axis([0 1 0 1])
   grid on
   xlabel('城市位置横坐标')
   ylabel('城市位置纵坐标')
   % 计算最优路径长度
   [V1_max,V1_ind]=max(V1);
   citys_end=citys(V1_ind,:);
   Length_end=dist(citys_end(1,:),citys_end(end,:)');
   for i=2:size(citys_end,1)
       Length_end=Length_end+dist(citys_end(i-1,:),citys_end(i,:)');
   end
   disp('最优路径矩阵');V1
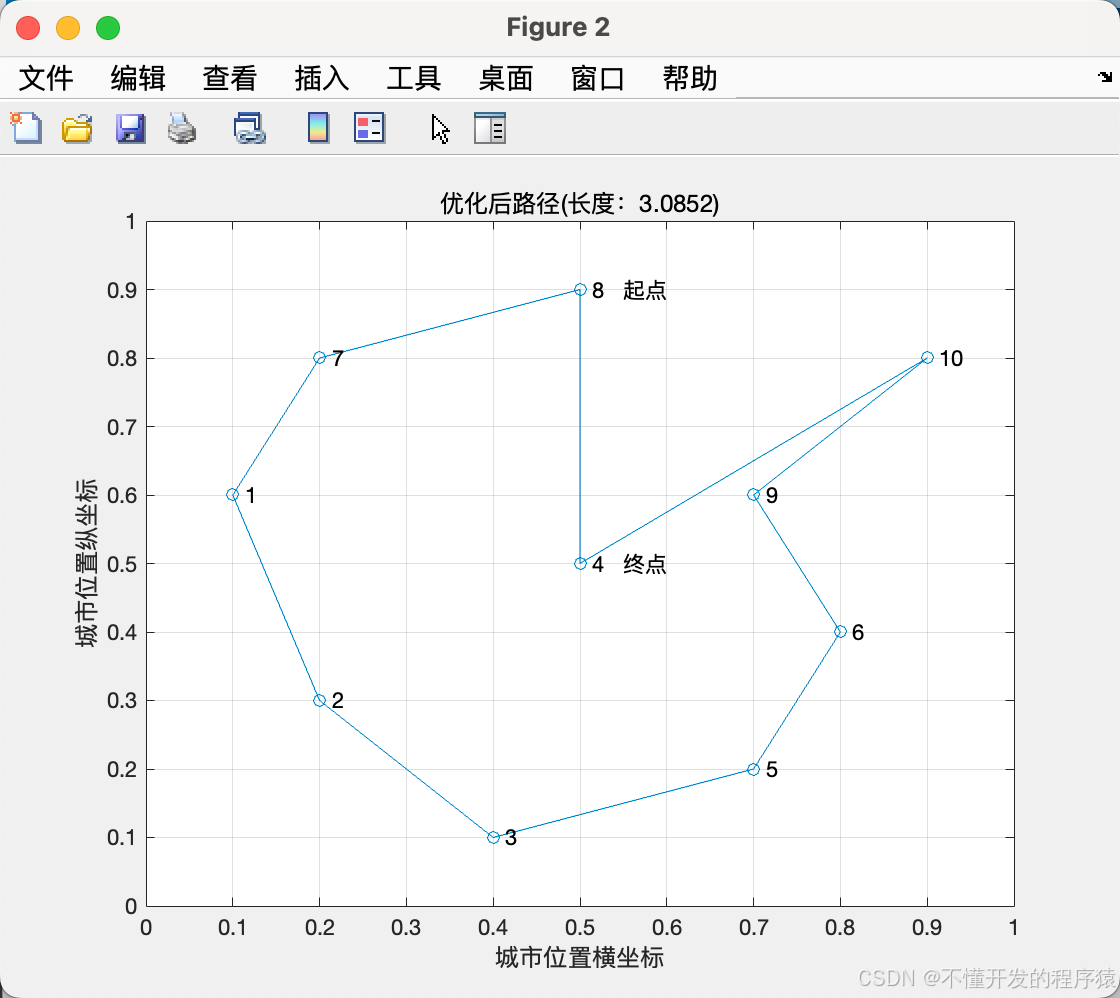
   % 绘制最优路径
   figure(2)
   plot([citys_end(:,1);citys_end(1,1)],...
       [citys_end(:,2);citys_end(1,2)],'o-')
   for i=1:length(citys)
       text(citys(i,1),citys(i,2),['  ' num2str(i)])
   end
   text(citys_end(1,1),citys_end(1,2),['       起点' ])
   text(citys_end(end,1),citys_end(end,2),['       终点' ])
   title(['优化后路径(长度：' num2str(Length_end) ')'])
   axis([0 1 0 1])
   grid on
   xlabel('城市位置横坐标')
   ylabel('城市位置纵坐标')
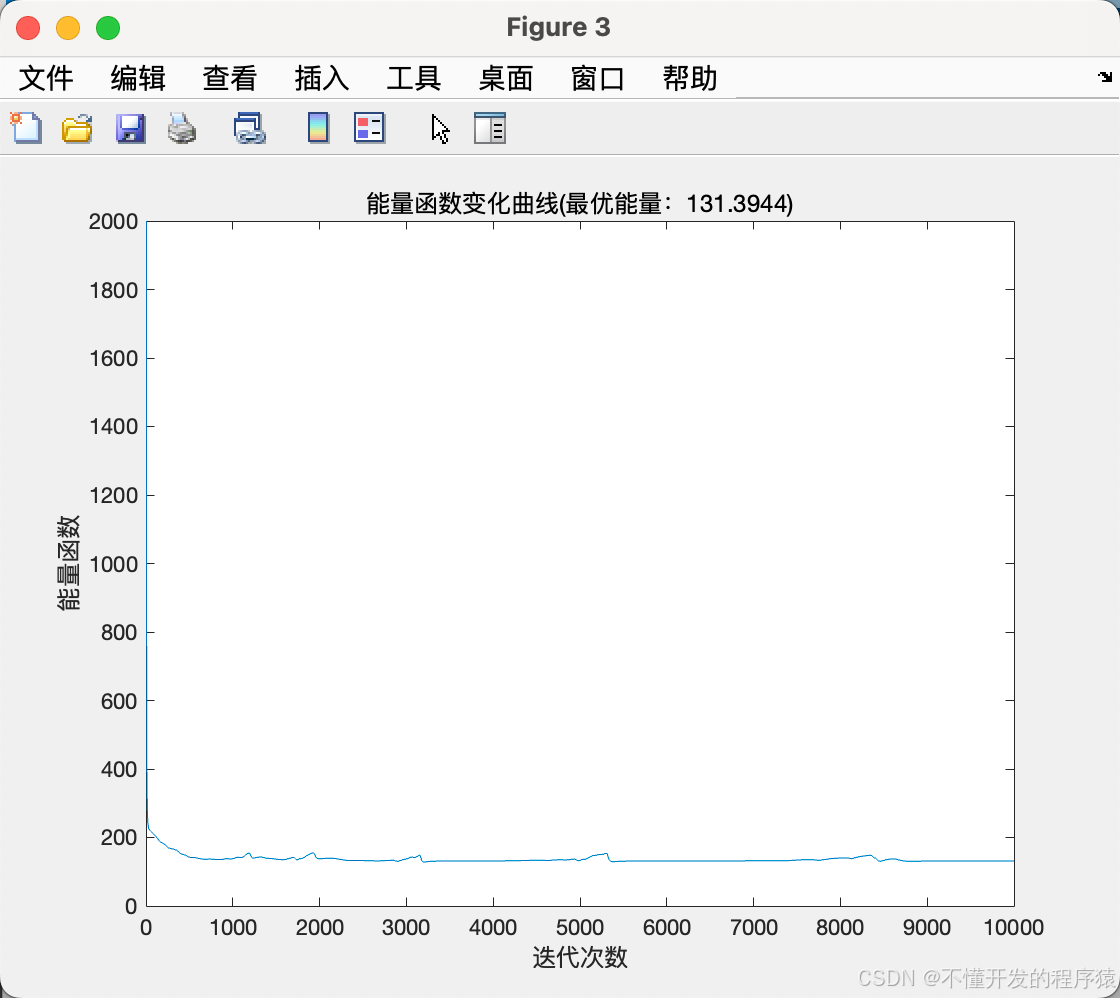
   % 绘制能量函数变化曲线
   figure(3)
   plot(1:iter_num,E);
   ylim([0 2000])
   title(['能量函数变化曲线(最优能量：' num2str(E(end)) ')']);
   xlabel('迭代次数');
   ylabel('能量函数');
else
   disp('寻优路径无效');
end

% %===========================================
% function du=diff_u(V,d)
% global A D
% n=size(V,1);
% sum_x=repmat(sum(V,2)-1,1,n);
% sum_i=repmat(sum(V,1)-1,n,1);
% V_temp=V(:,2:n);
% V_temp=[V_temp V(:,1)];
% sum_d=d*V_temp;
% du=-A*sum_x-A*sum_i-D*sum_d;
% %==========================================
% function E=energy(V,d)
% global A D
% n=size(V,1);
% sum_x=sumsqr(sum(V,2)-1);
% sum_i=sumsqr(sum(V,1)-1);
% V_temp=V(:,2:n);
% V_temp=[V_temp V(:,1)];
% sum_d=d*V_temp;
% sum_d=sum(sum(V.*sum_d));
% E=0.5*(A*sum_x+A*sum_i+D*sum_d);

最优路径矩阵

V1 =

     0     1     0     0     0     0     0     0     0     0
     0     0     1     0     0     0     0     0     0     0
     0     0     0     1     0     0     0     0     0     0
     0     0     0     0     0     1     0     0     0     0
     0     0     0     0     1     0     0     0     0     0
     0     0     0     0     0     0     1     0     0     0
     1     0     0     0     0     0     0     0     0     0
     0     0     0     0     0     0     0     0     0     1
     0     0     0     0     0     0     0     1     0     0
     0     0     0     0     0     0     0     0     1     0

>>

在这里插入图片描述

2.3 离散Hopfield神经网络求解旅行商问题优化计算

%% 离散Hopfield神经网络的优化―旅行商问题优化计算
% function TSP_hopfield()
%% 清空环境变量、定义全局变量
clc % 清屏
clear all; % 删除workplace变量
close all; % 关掉显示图形窗口
% step 1
A=1.5;
D=1;
u0=0.02;
step=0.01;
% step 2
N=8;
citys=[0.1,0.1;0.9,0.5;0.9,0.1;0.45,0.9;0.9,0.8;0.7,0.9;0.1,0.45;0.45,0.1];
Initial_Length=Initial_RouteLength(citys);        % 计算初始路径长度
DistanceCity=dist(citys,citys');
% step 3
u=2*rand(N,N)-1;
U=0.5*u0*log(N-1)+u;
V=(1+tanh(U/u0))/2;

for k=1:1:2000
    times(k)=k;
%     step 4
    dU=DeltaU(V,DistanceCity,A,D);
%     step 5
    U=U+dU*step;
%     step 6
    V=(1+tanh(U/u0))/2;
%     step 7 计算能量函数
    E=Energy(V,DistanceCity,A,D);
    Ep(k)=E;
%     step 8 检查路径合法性
    [V1,CheckR]=RouteCheck(V);
end

% step 9
if (CheckR==0)
    Final_E=Energy(V1,DistanceCity,A,D);
    Final_Length=Final_RouteLength(V1,citys);       % 计算最终路径长度
    disp('迭代次数');k
    disp('寻优路径矩阵：');V1
    disp('最优能量函数：');Final_E
    disp('初始路程：');Initial_Length
    disp('最短路程：');Final_Length
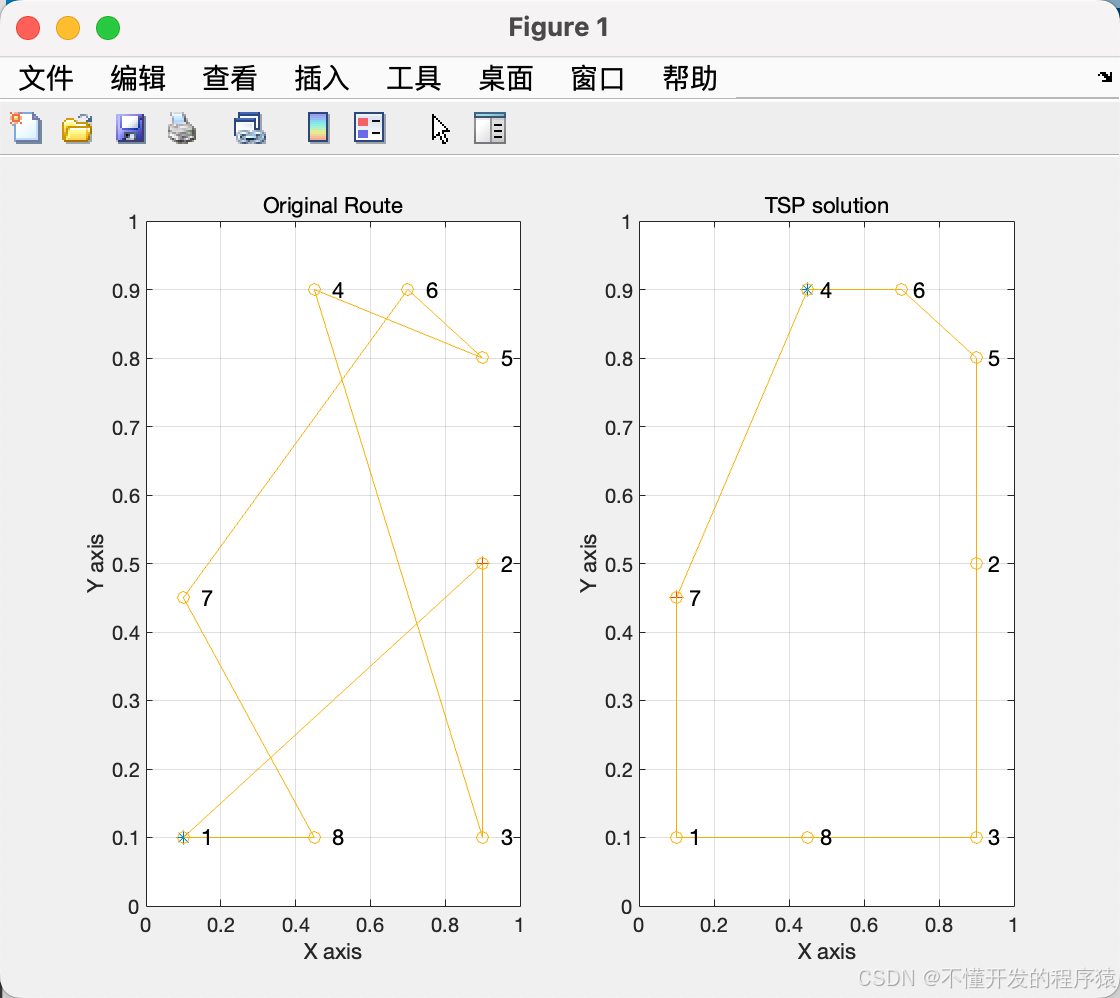
    PlotR(V1,citys);    % 寻优路径作图
else
    disp('寻优路径无效');
end

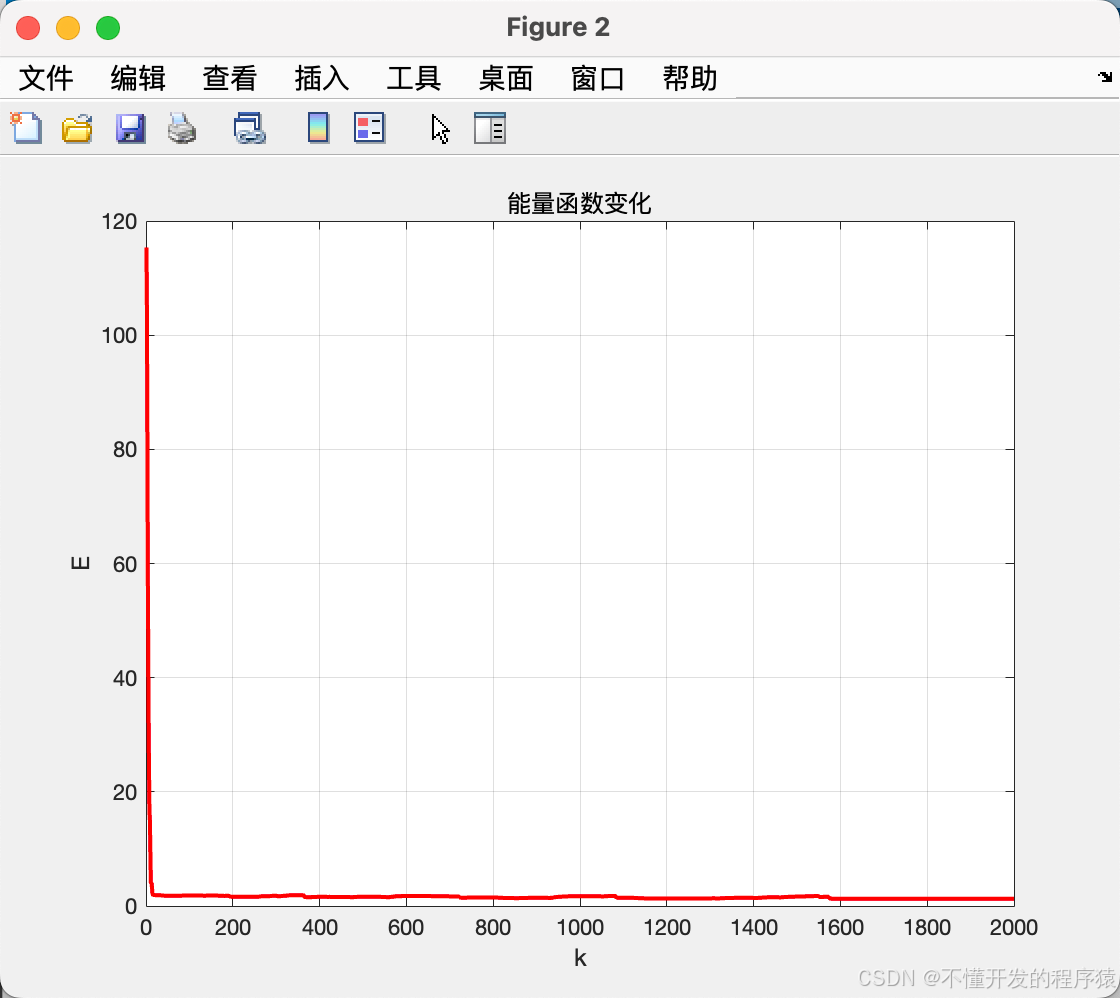
figure(2);
plot(times,Ep,'r','linewidth',2);
title('能量函数变化');
xlabel('k');
ylabel('E');
grid on

迭代次数

k =

        2000

寻优路径矩阵：

V1 =

     0     0     1     0     0     0     0     0
     0     0     0     0     0     1     0     0
     0     0     0     0     1     0     0     0
     1     0     0     0     0     0     0     0
     0     0     0     0     0     0     1     0
     0     0     0     0     0     0     0     1
     0     1     0     0     0     0     0     0
     0     0     0     1     0     0     0     0

最优能量函数：

Final_E =

   1.446847255149774

初始路程：

Initial_Length =

   4.491863945979413

最短路程：

Final_Length =

   2.893694510299548

>>