机器学习——boosting之XGBoost(推导+手动代码）

看了几篇，总感觉这个XGBoost不仅仅是对GBDT的改进版，还包含了对CART决策树的改进。书上说，XGBoost有很好的性能，在各大比赛中大放异彩，行吧，冲这句，好好看看！划水一整天，模型看了仨！不错，虽然现在在打哈欠，还是很想把XGBoost梳理梳理。这仨都是前k-1轮的，相当于常数。

# JFZero

693人浏览 · 2023-09-07 19:27:55

# JFZero · 2023-09-07 19:27:55 发布

划水一整天，模型看了仨！不错，虽然现在在打哈欠，还是很想把XGBoost梳理梳理
先从名字开始

XGBoost，eXtreme Gradient Boosting: em。。。。不理解

书上说，XGBoost有很好的性能，在各大比赛中大放异彩，行吧，冲这句，好好看看！

看了几篇，总感觉这个XGBoost不仅仅是对GBDT的改进版，还包含了对CART决策树的改进

1. 首先，GBDT是经过泰勒一阶导出来的，XGBoost则是经过泰勒二阶导，越高阶导越接近原函数值

初始的平方损失函数为 $L_{original} = (y_i-y_{pre})^2$ ，由于 $y_{pre}$ 是由 $y_{pre}=f(x)=∑_{i=1}^mf_i(x)$

因此， $L_{original}=L(y,f(x))，表示由y和f(x)影响L值$

$L_{m-1}(y,f_{m-1}(x))+\frac{ə_{L(y,f_{m-1}(x))}}{ə_{f_{m-1}(x)}}*[f(x)-f_{m-1}(x)]+\frac{1}{2}*\frac{ə^2_{L(y,f_{m-1}(x))}}{ə^2_{f_{m-1}(x)}}*(f(x)-f_{m-1}(x))^2$

令 $gi=əL(yi,fm−1(xi))əfm−1(xi)g_i = \frac{ə_{L(y_i,f_{m-1}(x_i))}}{ə_{f_{m-1}(x_i)}}$ ， $hi=əL(y,fm−1(xi))2əfm−1(xi)2h_i = \frac{ə^2_{L(y,f_{m-1}(x_i))}}{ə^2_{f_{m-1}(x_i)}}$ ， $L(y,f_{m-1}(x))$ 这仨都是前m-1轮的，相当于常数

令 $f(x)=f_m(x)$ ，则有 $T_m = f_m(x)-f_{m-1}(x)$

则 $Lm(y,fm(x))=Lm−1(y,fm−1(x))+∑i=1Ndatagi∗Tm(xi,θm)+12∑i=1Ndatahi∗Tm2(xi,θm)L_m(y,f_m(x)) = L_{m-1}(y,f_{m-1}(x))+∑_{i=1}^{N_{data}}g_i*T_m(x_i,θ_m)+\frac{1}{2}∑_{i=1}^{N_{data}}h_i*T^2_m(x_i,θ_m)$

2. 其次，XGBoost的优化①：增加正则化项 $Ω(T_m(x))$

晕了…明天再说！
本来周末把书带回家，准备要看看…果然，美男误我…

这里的 $Ω(T_m(x)) = γ*N_{叶}+λ∑_{i=1}^{N_{叶}}C_{i}^2(x)$ ，这里的 $N_叶$ 表示所有叶子节点的个数， $C_{i}(x)$ 是叶子节点的均值

$γ*N_{叶}$ 是对叶子节点个数的惩罚，毕竟如果分裂太多，容易过拟合

但 $λ∑_{i=1}^{N_{叶}}C_{i}^2(x)$ 是为什么要对叶子均值进行惩罚呢？

哦！

因为在XGBoost中，每个叶子节点的均值，其实都是这组叶子节点的残差均值

但有些残差是正的，有些是负的，那要衡量拟合效果是否好，应该看与0的差距。

残差为0，表示完美拟合
残差为正，表示大于原值
残差为负，表示小于原值

那么为了统一表示拟合效果，直接求平方，可避免正、负判别，且计算起来比绝对值更方便。

因此， $λ∑_{i=1}^{N_{叶}}C_{i}^2(x)$ 主要是对残差的惩罚

所以有 $Ω(T_m(x)) = γ*N_{叶}+λ∑_{i=1}^{N_{叶}}C_{i}^2(x)$ ，完成了对叶子数量和残差的惩罚

惩罚项也加入到 $L_K$ 损失函数里

$Lm(y,fm(x))=Lm−1(y,fm−1(x))+∑i=1Ndatagi∗Tm(xi,θm)+12∑i=1Ndatahi∗Tm2(xi,θm)+γ∗N叶+λ∑i=1N叶Ci2(x)L_m(y,f_m(x)) = L_{m-1}(y,f_{m-1}(x))+∑_{i=1}^{N_{data}}g_i*T_m(x_i,θ_m)+\frac{1}{2}∑_{i=1}^{N_{data}}h_i*T^2_m(x_i,θ_m)+ γ*N_{叶}+λ∑_{i=1}^{N_{叶}}C_{i}^2(x)$

求这个损失函数的极小值，求极值的时候，常数项不需要参与运算，因此函数里可以去掉常数项 $L_{m-1}(y,f_{m-1}(x))$ ，并且为了求极值计算方便，还可以将平方项 $λ∑_{i=1}^{N_{叶}}C_{i}^2(x)$ 的系数，设为 $12\frac{1}{2}$ 这样后续求极值时可以化简运算

最终 $Lm(y,fm(x))=∑i=1Ndatagi∗Tm(xi,θm)+12∑i=1Ndatahi∗Tm2(xi,θm)+γ∗N叶+12λ∑i=1N叶Ci2(x)L_m(y,f_m(x)) =∑_{i=1}^{N_{data}}g_i*T_m(x_i,θ_m)+\frac{1}{2}∑_{i=1}^{N_{data}}h_i*T^2_m(x_i,θ_m)+ γ*N_{叶}+\frac{1}{2}λ∑_{i=1}^{N_{叶}}C_{i}^2(x)$

这里要梳理一下 $N_{data}和N_{叶}$ 的关系
在这里插入图片描述
所以，可以将损失函数里式子进行转化

$_{i=1}^{N_{data}}g_i*T_m(x_i,θ_m)=∑_{j=1}^{N_{叶}}（∑_{i∈I(j)}g_i）C_{j}(x)$ ，用 $G_j表示∑_{i∈I(j)}g_i$
$∑i=1Ndatahi∗Tm2(xi,θm)=∑j=1N叶（∑i∈I(j)hi）Cj2(x)∑_{i=1}^{N_{data}}h_i*T^2_m(x_i,θ_m)=∑_{j=1}^{N_{叶}}（∑_{i∈I(j)}h_i）C_{j}^2(x)$ ，用 $H_j表示∑_{i∈I(j)}h_i$

则损失函数为
$Lm(y,fm(x))=∑j=1N叶GjCj(x)+12∑j=1N叶HjCj2(x)+γ∗N叶+12λ∑j=1N叶Cj2(x)+λN叶L_m(y,f_m(x)) =∑_{j=1}^{N_{叶}}G_jC_{j}(x)+\frac{1}{2}∑_{j=1}^{N_{叶}}H_jC_{j}^2(x)+ γ*N_{叶}+\frac{1}{2}λ∑_{j=1}^{N_{叶}}C_{j}^2(x)+λN_{叶}$

合并同类项：

$L_m(y,f_m(x))$

$=∑j=1N叶GjCj(x)+12∑j=1N叶（Hj+λ）Cj2(x)+γ∗N叶=∑_{j=1}^{N_{叶}}G_jC_{j}(x)+\frac{1}{2}∑_{j=1}^{N_{叶}}（H_j+λ）C_{j}^2(x)+ γ*N_{叶}$

$=∑j=1N叶[GjCj(x)+12(Hj+λ)Cj2(x)+γ]=∑_{j=1}^{N_{叶}}[G_jC_{j}(x)+\frac{1}{2}(H_j+λ)C_{j}^2(x)+ γ]$

$Gj=∑i∈I(j)gi=∑i∈I(j)əL(yi,fm−1(xi))əfm−1(xi)G_j=∑_{i∈I(j)}g_i=∑_{i∈I(j)} \frac{ə_{L(y_i,f_{m-1}(x_i))}}{ə_{f_{m-1}(x_i)}}$ ，是常数项
$Hj=∑i∈I(j)hi=∑i∈I(j)əL(y,fm−1(xi))2əfm−1(xi)2H_j=∑_{i∈I(j)}h_i=∑_{i∈I(j)}\frac{ə^2_{L(y,f_{m-1}(x_i))}}{ə^2_{f_{m-1}(x_i)}}$ ，也是常数项
γ也是我们提前设置的常数项
只要计算出每个叶子节点中的 $GjCj(x)+12(Hj+λ)Cj2(x)+γG_jC_{j}(x)+\frac{1}{2}(H_j+λ)C_{j}^2(x)+ γ$ 极小值，就可以算出所有叶子节点 $∑j=1N叶GjCj(x)+12∑j=1N叶（Hj+λ）Cj2(x)+γ∗N叶∑_{j=1}^{N_{叶}}G_jC_{j}(x)+\frac{1}{2}∑_{j=1}^{N_{叶}}（H_j+λ）C_{j}^2(x)+ γ*N_{叶}$ 的极小值
$Lj=12(Hj+λ)Cj2(x)+GjCj(x)+γL_j =\frac{1}{2}(H_j+λ)C_{j}^2(x)+ G_jC_{j}(x)+ γ$ 相当于一元二次方程 $y = ax^2+bx+c$ ，在 $x=−b2ax=-\frac{b}{2a}$ 处可以取到极值 $4ac−b24a\frac{4ac-b^2}{4a}$
因此当 $Cj(x)=−GjHj+λC_{j}(x) = -\frac{G_j}{H_j+λ}$ 时，可以求到单个叶子节点的损失函数极小值 $min:Lj=2γ(Hj+λ)−Gj22(Hj+λ)=γ−Gj22(Hj+λ)min:L_j=\frac{2γ(H_j+λ)-G_j^2}{2(H_j+λ)}=γ-\frac{G_j^2}{2(H_j+λ)}$
那么第m次迭代时所有样本的损失函数为， $min:Lm(y,fm(x))=∑j=1N叶[γ−Gj22(Hj+λ)]min:L_m(y,f_m(x))=∑_{j=1}^{N_{叶}}[γ-\frac{G_j^2}{2(H_j+λ)}]$

3. 最后，XGBoost的决策树分裂的特征及特征值，与CART决策树选取标准是不同的

CART决策树是根据基尼系数最小，选取的特征及特征值来分裂树
而XGBoost是可以采用贪心算法，根据特征及特征值分裂后的损失函数增益最大值，来选取的特征及特征值来分裂树

损失函数增益，指的是，每次分裂一个节点时，损失值减小的程度
- 当前节点的损失值会发生改变，而其他节点的损失值不变。
- 如果当前节点的损失值比分裂前非常非常小，说明整体的损失值也会变小，增益程度也会更大
- 如果当前节点的损失值比分裂前差不多，说明整体的损失值没有太大改变，增益程度不大
- 因此，应该选择损失值增益最大的特征及特征值，作为分裂的节点

因此，
$=[γ-\frac{G_{j父}^2}{2(H_{j父}+λ)}]-[γ-\frac{G_{j左}^2}{2(H_{j左}+λ)}]-[γ-\frac{G_{j右}^2}{2(H_{j右}+λ)}]$

$=Gj左22(Hj左+λ)+Gj右22(Hj右+λ)−Gj父22(Hj父+λ)−γ=\frac{G_{j左}^2}{2(H_{j左}+λ)}+\frac{G_{j右}^2}{2(H_{j右}+λ)}-\frac{G_{j父}^2}{2(H_{j父}+λ)}-γ$

其中 $Gj父22(Hj父+λ)\frac{G_{j父}^2}{2(H_{j父}+λ)}$ ，

$G_{j父}=∑_{i∈I(j左+j右)}g_i=∑_{i∈I(j左)}g_i+∑_{i∈I(j右)}g_i = G_{j左}+G_{j右}$
$H_{j父}=∑_{i∈I(j左+j右)}h_i=∑_{i∈I(j左)}h_i+∑_{i∈I(j右)}h_i = H_{j左}+H_{j右}$

因此， $Gj父22(Hj父+λ)=(Gj左+Gj右)22(Hj左+Hj右+λ)\frac{G_{j父}^2}{2(H_{j父}+λ)}=\frac{(G_{j左}+G_{j右})^2}{2(H_{j左}+H_{j右}+λ)}$

所以最终的
$Gain=Gj左22(Hj左+λ)+Gj右22(Hj右+λ)−Gj父22(Hj父+λ)−γGain=\frac{G_{j左}^2}{2(H_{j左}+λ)}+\frac{G_{j右}^2}{2(H_{j右}+λ)}-\frac{G_{j父}^2}{2(H_{j父}+λ)}-γ$

$=Gj左22(Hj左+λ)+Gj右22(Hj右+λ)−(Gj左+Gj右)22(Hj左+Hj右+λ)−γ=\frac{G_{j左}^2}{2(H_{j左}+λ)}+\frac{G_{j右}^2}{2(H_{j右}+λ)}-\frac{(G_{j左}+G_{j右})^2}{2(H_{j左}+H_{j右}+λ)}-γ$

因此，最终是根据Gain最大的结果，来选取最优的分裂特征及特征值

完美！

程序设计

1. 数据结构：一棵二叉树

每个节点存储的数据：
- 当前节点的样本残差集
- 选择分裂的特征及特征值

2. 实现流程：核心步骤

获取当前节点的所有特征及特征值
遍历每个特征及特征值
- 根据当前特征及特征值分两组
- 计算G左、G右
  - $Gi=∑i∈I(j)əL(yi,fm−1(xi))əfm−1(xi)G_i=∑_{i∈I(j)} \frac{ə_{L(y_i,f_{m-1}(x_i))}}{ə_{f_{m-1}(x_i)}}$
  - $L(y_i,f_{m-1}(x_i))=(y_i-y_{pre})^2=[y_i-f_{m-1}(x_i)]^2$
  - $Gi=∑i∈I(j)əL(yi,fm−1(xi))əfm−1(xi)=∑i∈I(j)[−2(yi−fm−1(xi))]G_i=∑_{i∈I(j)} \frac{ə_{L(y_i,f_{m-1}(x_i))}}{ə_{f_{m-1}(x_i)}}=∑_{i∈I(j)} [-2(y_i-f_{m-1}(x_i))]$
- 计算H左、H右
  - $Hi=∑i∈I(j)əL(yi,fm−1(xi))2əfm−1(xi)=∑i∈I(j)[−2(yi−fm−1(xi))]′=∑i∈I(j)2yiH_i=∑_{i∈I(j)} \frac{ə^2_{L(y_i,f_{m-1}(x_i))}}{ə_{f_{m-1}(x_i)}}=∑_{i∈I(j)} [-2(y_i-f_{m-1}(x_i))]'=∑_{i∈I(j)} 2y_i$
- 计算分组后的Gain值，记录最大值及对应的特征、特征值
  - $Gain=Gj左22(Hj左+λ)+Gj右22(Hj右+λ)−(Gj左+Gj右)22(Hj左+Hj右+λ)−γGain=\frac{G_{j左}^2}{2(H_{j左}+λ)}+\frac{G_{j右}^2}{2(H_{j右}+λ)}-\frac{(G_{j左}+G_{j右})^2}{2(H_{j左}+H_{j右}+λ)}-γ$
判断Gain最大值情况下，是否可以分裂左右组
- 条件：Gain大于0 则可以分裂，否则停止分裂
将最终划分的两个组，设置为左右节点分裂，再分别递归划分

实践遇到的问题

问题1：XGBoost到底是一棵树还是多棵树？

显然是多棵树

问题2：那第一棵树的第一个分裂节点，没有 $y_{pre}$ 怎么计算G值，怎么计算Gain值?
没有Gain值，怎么选择分裂节点？

直击灵魂深处，万事开头难，古人诚不欺我也

所以，为了踏出第一步，需要提前设置一个 $y_{pre0}$ 初始预测值
这里，可以设置为 $y_{pre0}=average(y_{true})$ ，表示第0棵树的所有样本预测值为所有样本真实值的均值,并记录当前预测值 $f_0(x)=y_{pre0}$ ，计算出初始残差值 $r_0$

1、计算出初始残差值 $r_0$ 后，开始建立第一棵树
- 先分裂节点：
  - ①获取当前节点的所有特征及特征值
  - ②遍历特征及特征值，计算出最大gain
  - ③判断是否可以分裂
  - ④完成分裂，左右树递归
- 再进行预测：
  - ①预测所有样本的预测值 $y_{pre1}$
  - ②计算当前所有树的预测结果 $f_{1}(x)=f_0(x)+y_{pre1}$
2、计算出第一棵树的残差值 $r_1=y-f_{1}(x)$ 后，开始建立第二棵树
- 先分裂节点：
  - ①获取当前节点的所有特征及特征值
  - ②遍历特征及特征值，计算出最大gain
  - ③判断是否可以分裂
  - ④完成分裂，左右树递归
- 再进行预测：
  - ①预测所有样本的预测值 $y_{pre2}$
  - ②计算当前所有树的预测结果 $f_{2}=f_1(x)+y_{pre2}$
…
这里要区分 $f_m(x)和y_{pre}$ 的定义
- $f_m(x)$ 是对实际y值拟合的预测值， $y_{pre}$ 是对上一轮的残差拟合的预测值， $T(x)=y_{pre}$

应该是这样的，估计要创建树的多个对象，然后维护一个全局的数据样本残差表，然后依次根据每棵树对象来更新这个样本残差表

最后模型保留的，就是每棵树以及树的结构，树里每个节点都保留分裂的特征及特征值，保留叶子节点的均值

最终代码

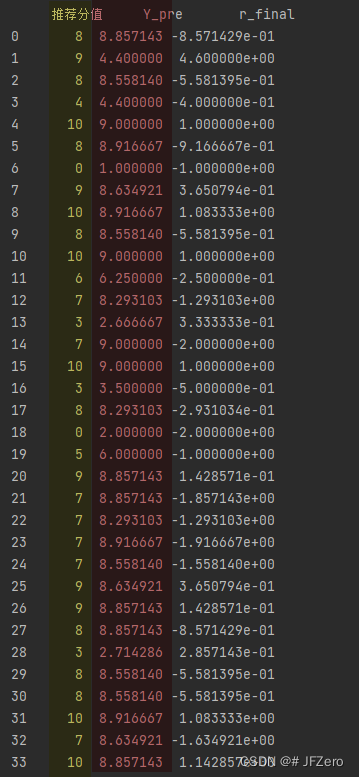
最终我只建了10棵树，我还没想好树的数量标准
但10棵树的预测效果，还是不错的，虽然不确定会不会过拟合，但以后有时间再验证

终于可以进入聚类了~~~~~

在这里插入图片描述

import numpy as np
import pandas as pd
import warnings
warnings.filterwarnings('ignore')
pd.set_option('display.max_rows',None)
# 获取所需数据：'推荐分值', '专业度','回复速度','服务态度','推荐类型'
datas = pd.read_excel('./datas4.xlsx')
important_features = ['专业度','回复速度','服务态度','推荐分值'] #
datas_1 = datas[important_features]
Y_features = '推荐分值'
X_features = X.columns

class Node():
    def __init__(self,datas):
        self.datas = datas
        self.all_feat_and_point = self.get_feat_points(datas)
        self.feat = None
        self.point = None
        self.mean = None
        self.left = None
        self.right = None
    def get_feat_points(self,datas):
        """计算出每个节点的特征及特征值"""
        feats = X_features
        feat_and_point = {}
        for feat in feats:
            feat_and_point[feat]= datas[feat].unique()
        return feat_and_point

class Tree():
    def __init__(self,datas,gama=1):
        self.datas = datas
        self.gama = gama
        self.root = Node(self.datas)
    def devide(self,node=None):
        """选择特征及特征值，进行递归分裂"""
        node.mean = node.datas['r'].mean(axis=0)
        max_gain = None
        for feat,points in node.all_feat_and_point.items():
            for point in points:
                value = self.get_gain(feat,point,node.datas)
                if max_gain==None or value['gain']>max_gain:
                    max_gain = value['gain']
                    temp_feat = feat
                    temp_point = point
                    left_datas = value['left_datas']
                    right_datas = value['right_datas']
        if max_gain<10**-7 or left_datas.empty or right_datas.empty:
            return
        node.feat = temp_feat
        node.point = temp_point
        node.left = Node(left_datas)
        node.right = Node(right_datas)
        self.devide(node.left)
        self.devide(node.right)
    
    def get_gain(self,feat,point,datas):
        """计算Gain值"""
        value = {}
        left_datas = datas[datas[feat]<=point]
        right_datas = datas[datas[feat]>point]
        G_left = 2*left_datas['Fm'].sum(axis=0)-2*left_datas[Y_features].sum(axis=0)
        G_right = 2 * right_datas['Fm'].sum(axis=0) - 2 * right_datas[Y_features].sum(axis=0)
        H_left = 2 * left_datas[Y_features].sum(axis=0)
        H_right = 2 * right_datas[Y_features].sum(axis=0)
        gain = G_left**2/(2*H_left+2*self.gama)+G_right**2/(2*H_right+2*self.gama)+(G_left+G_right)**2/(2*H_left+2*H_right+2*self.gama)
        value['gain'] = gain
        value['left_datas'] = left_datas
        value['right_datas'] = right_datas
        return value
    def get_new_datas(self):
        Y_pre = []
        for index,data in self.datas.iterrows():
            temp = self.find_Y(data,self.root)
            Y_pre.append(temp)
        self.datas['r'] = self.datas['r']-Y_pre
        self.datas['Fm'] = self.datas['Fm']+Y_pre
        return self.datas
    def find_Y(self,data,node=None):
        feat = node.feat
        point = node.point
        if feat == None:
            return node.mean
        if data[feat]<=point:
            return self.find_Y(data,node.left)
        else:
            return self.find_Y(data,node.right)

class XGB():
    def __init__(self,datas,gama=1):
        self.datas = datas
        self.gama = gama
        self.end = 10 # 建多少棵树
        self.trees = []
        self.Fm = datas[Y_features].mean(axis=0)
        self.datas['Fm'] = [self.Fm for i in range(len(self.datas))]
        self.datas['r'] = self.datas[Y_features] - self.Fm
    def learning(self):
        for i in range(self.end):
            tree = Tree(self.datas,self.gama)
            tree.devide(tree.root)
            self.datas = tree.get_new_datas()  # 更新r和fm值
            self.trees.append(tree)
        return self.trees
    def predict(self,datas):
        Y_pre = []
        for index,data in datas.iterrows():
            fm = self.Fm
            for tree in self.trees:
                temp = tree.find_Y(data,tree.root)
                fm += temp # 累计每棵树的fm，作为最终的预测值
            Y_pre.append(fm)
        return Y_pre

tree = XGB(datas_1)
tree.learning()
Y_pre = tree.predict(datas_1)

datas_1['Y_pre'] = Y_pre
datas_1['r_final'] = datas_1[Y_features]-datas_1['Y_pre']
print(datas_1[[Y_features,'Y_pre','r_final']])

技术共进，成长同行——讯飞AI开发者社区

更多推荐

2025大数据时代哪些证书可以考：推荐8个最合适考的证书

讯飞AI开发者社区

人工智能知识体系全景图：从基础概念到2025年前沿技术（一）

讯飞AI开发者社区

从数据分析师到提示工程架构师：技能转化与路径规划

在人工智能技术迅猛发展的今天，提示工程架构师已成为连接数据洞察与AI能力的关键角色。本文系统阐述了数据分析师向提示工程架构师转型的理论基础、技能迁移路径与实践策略。通过构建"技能转化矩阵"和"能力迁移四象限"模型，本文提供了一套结构化方法论，帮助数据分析师识别核心可迁移技能、弥补知识差距，并通过渐进式学习路径实现职业升级。文章深入剖析了提示工程架构师的角色定位、能力需求和行业价值，提供了从基础提示