请添加图片描述

前言

这周因为不能出去就尽量把数据结构更完，每天一篇文章发布，请大家监督我，如果我没法请@我催更0.0
三连即可提高学习效率0.0

🧑🏻作者简介：一个学嵌入式的年轻人
✨联系方式：2201891280(QQ)
📔源码地址：https://gitee.com/xingleigao/study_qianrushi
⏳全文大约阅读时间： 120min

文章目录

栈

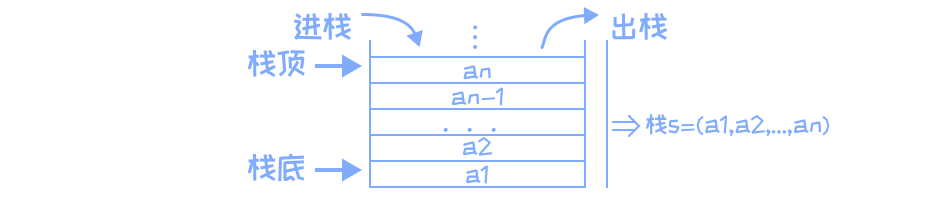
栈是限制在一端进行插入操作和删除操作的线性表（俗称堆栈）。
相关的术语：

  • 允许进行操作的一端成为栈顶
  • 另一固定端成为栈底
  • 当栈中没有元素时成为空栈
    特点：后进先出

请添加图片描述

顺序栈

他是顺序表的一种,具有顺序表永阳的存储结构,由数组定义,配合用数组下标表示的栈顶指针top(相对指针)完成各种操作。
定义方式如下:

typedef int data_t;	//定义栈中数据元素的数据类型
typedef struct{
	data_t *data;	//用指针指向栈的存储空间
	int maxlen;	//当前栈的最大元素大小
	int top;		//只是栈顶元素位置
}sqstack;

创建

请添加图片描述
示例代码：

sqstack * stack_create(int len){
       sqstack * s;
       if ((s = (sqstack *)malloc(sizeof(sqstack)))== NULL){
               printf("malloc sqstack failed\n");
               return NULL;
       }

       if((s->data = (data_t *)malloc(sizeof(data_t) * len))==NULL){
               printf("malloc data failed\n");
               free(s);
               return NULL;
       }

       memset(s->data, 0 , len * sizeof(data_t));
       s->maxlen = len;
       s->top = -1;
       return s;
}

入栈

请添加图片描述
示例代码：

int stack_push(sqstack * s, data_t value){

       if(s == NULL){
               puts("stack is null");
               return -1;
       }

        if(s->top == s->maxlen - 1){	//判断是否为空
                puts("stack is full");
                return -1;
        }

       s->top++;
       s->data[s->top] = value;

       return 0;
}

出栈

请添加图片描述
示例代码：

data_t stack_pop(sqstack * s){
       s->top--;
       return (s->data[s->top+1]);
}

其他的操作相对比较简单，建议直接看我gitee上的代码。

链式栈

插入操作和删除操作均在链表头部进行，链表尾部就是栈底，栈顶指针就是头指针。
请添加图片描述
数据类型定义：

typedef int data_t;
typedef struct node_t{
	data_t data;
	struct node_t *next;
}linkstack_t;

这部分比较简单就直接给相关实现的源码了：

linkstack stack_create(){
        linkstack s;

        s = (linkstack)malloc(sizeof(listnode));
        if(s == NULL){
                puts("malloc failed");
                return NULL;
        }
        s->data = 0;
        s->next = NULL;
        return s;
}

int stack_push(linkstack s, data_t value){
        linkstack p;

        if(s == NULL){
                puts("s is null");
                return -1;
        }

        p = (linkstack)malloc(sizeof(listnode));
        if(p == NULL){
                puts("malloc failed");
                return -1;
        }
        p->data = value;
        //p->next = NULL;

        p->next = s->next;
        s->next = p;

        return 0;
}

data_t stack_pop(linkstack s){
        linkstack p;

        p = s->next;
        s->next = p->next;

        data_t t = p->data;
        free(p);
        p = NULL;

        return t;
}

int stack_empty(linkstack s){
        if(s == NULL){
                puts("s is null");
                return -1;
        }
        return (s->next == NULL ? 1 : 0);
}

data_t stack_top(linkstack s){
        return (s->next->data);
}

linkstack stack_free(linkstack s){
        linkstack p;

        if(s == NULL){
                puts("s is null");
                return NULL;
        }

        while(s != NULL){
                p = s;
                s = s->next;
                printf("free:%d\n", p->data);
                free(p);
        }
        return NULL;

}

队列

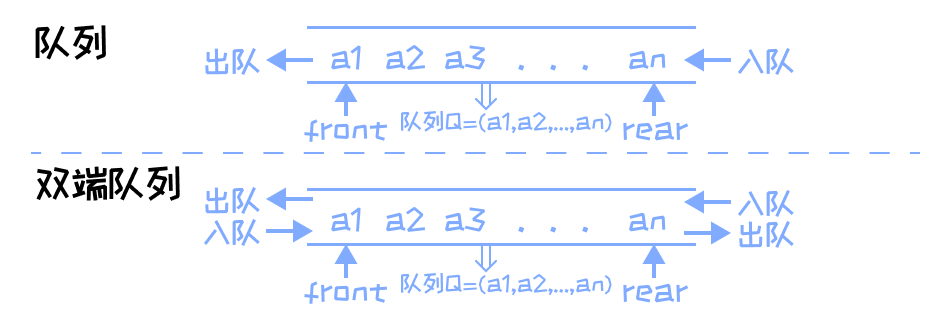
队列是限制在两端进行插入操作和删除操作的线性表

  • 允许进行存入操作的一端称为队尾
  • 允许进行删除操作的一端称为队头
  • 当线性表中没有元素时，成为空队
    特点：先入先出(FIFO)

请添加图片描述

队列的操作

  • 创建队列：CreateQueue()
  • 清空队列：ClearQueue(Q)
  • 判断队列空：EmptyQueue(Q)
  • 判断队列满：FullQueue(Q)
  • 入队：EnQueue(Q,x)
  • 出队：DeQueue(Q)

顺序队列

顺序队列的数据结构

typedef int datatype;
#define N 128

typedef struct{
       datatype data[];
       int front;
       int rear;
}

因为之前相关操作都是差不多的，需要注意的只有是循环队列，所以判断条件不太一样，这里相关操作我也直接给代码了：

sequeue *queue_create(){
        sequeue *sq;

        if((sq = (sequeue *)malloc(sizeof(sequeue))) == NULL){
                printf("malloc failed\n");
                return NULL;
        }

        memset(sq->data,0,sizeof(sq->data));
        sq->front = sq->rear = 0;

        return sq;

}

int enqueue(sequeue *sq, datatype x){
        if(sq == NULL){
                printf("sq is null\n");
                return -1;
        }

        if ((sq->rear + 1) % N == sq->front){
                printf("sequeue is full\n");
                return -1;
        }

        sq->data[sq->rear] = x;
        sq->rear = (sq->rear + 1) % N;

        return 0;
}

datatype dequeue(sequeue *sq){
        if(sq == NULL){
                printf("sq is null\n");
                return -1;
        }
        datatype ret;

        ret = sq->data[sq->front];

        sq->front = (sq->front + 1) % N;

        return ret;
}

int queue_empty(sequeue *sq){
        if(sq == NULL){
                printf("sq is null\n");
                return -1;
        }
        return (sq->front == sq->rear ? 1 : 0);
}

int queue_full(sequeue *sq){
        if(sq == NULL){
                printf("sq is null\n");
                return -1;
        }
        if ((sq->rear + 1) % N == sq->front){
                return -1;
        }
        return 0;
}

int queue_clear(sequeue *sq){
        if(sq == NULL){
                printf("sq is null\n");
                return -1;
        }
        sq->front = sq->rear = 0;
        return 0;
}

sequeue * queue_free(sequeue *sq){
        if(sq == NULL){
                printf("sq is null\n");
                return NULL;
        }
        free(sq);
        sq = NULL;
        return sq;
}

一般队列的使用不会声明这么多的结构体啥的，一般都是直接使用一个数组来当作队列使用。出队入队都是一行代码。可以想想怎么写，有时间写个demo。

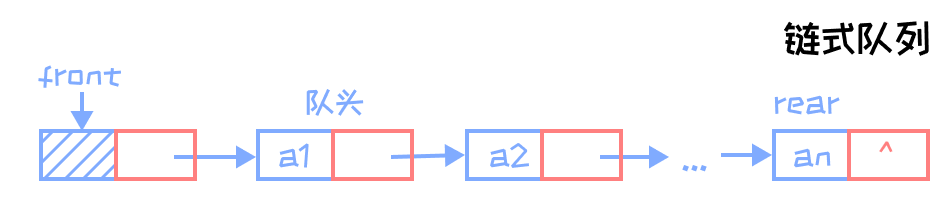
链式队列

插入操作在队尾进行，删除操作在队头进行，由队头指针和队尾指针控制队列的操作。
请添加图片描述
结构体定义：

相关操作

linkqueue * queue_create(){
        linkqueue *lq;

        if((lq = (linkqueue *)malloc(sizeof(linkqueue))) == NULL){
                printf("malloc linkqueue failed\n");
                return NULL;
        }
        lq->front = lq->rear = (linklist)malloc(sizeof(listnode));
        if(lq->front == NULL){
                printf("malloc node failed\n");
                free(lq);
                return NULL;
        }
        lq->front->data = 0;
        lq->front->next = NULL;
        return lq;
}

int enqueue(linkqueue *lq, datatype x){
        linklist p;

        if(lq == NULL){
                printf("lq is null\n");
                return -1;
        }
        if((p = (linklist)malloc(sizeof(listnode))) == NULL){
                printf("malloc node failed\n");
                return -1;
        }
        p->data = x;
        p->next = NULL;

        lq->rear->next = p;
        lq->rear = p;

        return 0;
}

datatype dequeue(linkqueue *lq){
        linklist p;
        if(lq == NULL){
                printf("lq is null\n");
                return -1;
        }

        p = lq->front;
        lq->front = p->next;
        free(p);
        return lq->front->data;
}

int queue_empty(linkqueue *lq){
        if(lq == NULL){
                printf("lq is null\n");
                return -1;
        }
        return (lq->front == lq->rear ? 1: 0);
}

int queue_clear(linkqueue *lq){
        linklist p;

        if(lq == NULL){
                printf("lq is null\n");
                return -1;
        }
        if(!lq->front){
                return 0;
        }
        while(lq->front->next){
                p = lq->front;
                lq->front = p->next;
                printf("free:%d\n",p->data);
                free(p);
        }

        return 0;

}
linkqueue * queue_free(linkqueue *lq){
        linklist p;

        if(lq == NULL){
                printf("lq is null\n");
                return lq;
        }
        while(lq->front){
                p = lq->front;
                lq->front = p->next;
                printf("free :%d\n" ,p->data);
                free(p);
        }
        free(lq);
        return NULL;
}

栈和队列的应用

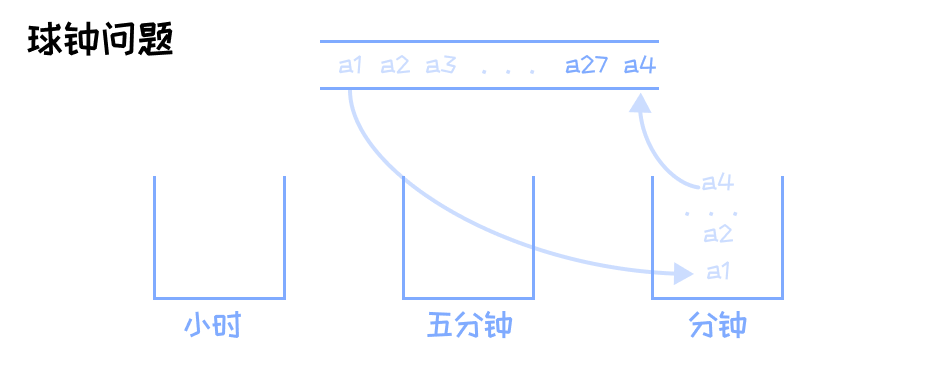
球钟是一个利用球的移动来记录时间的的简单装置。
它有三个可以容纳若干球的指示器：分钟指示器，五分钟指示器，小时指示器
如：分钟指示器有2个球，五分钟指示器6个球，小时指示器有5个球，则时间为5:32

工作原理：
每过一分钟，球钟就会从一个队列的队首取出一个球放入分钟指示器，分钟指示器最多可以容纳4个球。
当放入第5个球时，在分钟指示器的4个球就会按照他们被放入时的顺序加入球队列的队尾。而第五个球就会进入五分钟指示器。
按此类推，五分钟指示器最多可放11个球，小时指示器最多可以放11个球。
请添加图片描述

问题：
现设初始时队列的球数为27，球钟的三个指示器初始状态均为空。问：要经过多久，球队列才能回复到原来的顺序？

解决代码

#include <stdio.h>
#include "linkqueue.h"
#include "sqstack.h"

int check(linkqueue *lq);

int main(int argc, const char *argv[]){
        linkqueue *lq;
        sqstack *s_hour, *s_five, *s_min;
        int i, min = 0;
        int value;

        if((lq = queue_create()) == NULL){
                return -1;
        }

        for(i = 1; i <= 27; ++i){
                enqueue(lq,i);
        }

        if((s_hour = stack_create(11)) == NULL) return -1;
        if((s_five = stack_create(11)) == NULL) return -1;
        if((s_min = stack_create(4)) == NULL)   return -1;

        while(1){
                min++;
                if(!queue_empty(lq)){
                        value = dequeue(lq);
                        if(!stack_full(s_min)){
                                stack_push(s_min, value);
                        }else{
                                while(!stack_empty(s_min)){
                                        enqueue(lq, stack_pop(s_min));
                                }
                                if(!stack_full(s_five)){
                                        stack_push(s_five,value);
                                }else{
                                        while(!stack_empty(s_five)){
                                                enqueue(lq, stack_pop(s_five));
                                        }
                                        if(!stack_full(s_hour)){
                                                stack_push(s_hour,value);
                                        }else{
                                                while(!stack_empty(s_hour)){
                                                        enqueue(lq, stack_pop(s_hour));
                                                }
                                                enqueue(lq, value);
                                                if(check(lq) == 1)
                                                        break;
                                        }
                                }
                        }
                }


        }

        printf("total:%d\n",min);
        return 0;
}

int check(linkqueue *lq){
        linklist p;
        if(lq == NULL){
                printf("lq is null\n");
                return -1;
        }

        p = lq->front->next;

        while(p && p->next){
                if(p->data < p->next->data)
                        p = p->next;
                else return 0;
        }
        return 1;
}

写在最后

栈和队列内容有点多，我失策了，导致昨天没正常更新，今天很多内容需要去gitee仓库里找我练习的代码跟着写来理解，大家加油，接下来的几天时间会继续了解各种数据结构，我尽量一天一更，大家和我一起变强呀！最后三连即可提高学习效率！！！

另外我在更新的就是算法笔记的一些例题笔记，这个系列是用于提高我的算法能力，如果有兴趣对算法领域感兴趣找不到合适的入门文章也可以追更，如果我更新的太慢了请大家点赞收藏，一键三连才能更有更新的动力呀0.0

# 数据结构 # 链表 # c语言 # 嵌入式
Logo
技术共进，成长同行——讯飞AI开发者社区

技术共进，成长同行——讯飞AI开发者社区

更多推荐

cover

深度学习算法：开启智能时代的钥匙

avatar 讯飞AI开发者社区
cover

目标检测数据集 第017期-基于yolo标注格式的垃圾分类检测数据集(含免费分享)

avatar 讯飞AI开发者社区
cover

【人工智能】提示词进阶：用“思维链（CoT）”让大模型更擅长逻辑推理

avatar 讯飞AI开发者社区