目录

​编辑

一、说明：

二、能量基本概念

2.1 能量的一般概念

2.2 信号的能量

三、勾股定律和能量守恒

四、 能量和欧式距离

五、圆周上的能量守恒

六、方差和能量

---

一、说明：

        国内学生普遍认为，学完高等数学，数学就到头了。曾经谈论起数学，一位北大学子夸耀自己高数有多牛，那么高数之外还有没有数学，我告诉你们，高数仅仅是个预备活动，谈不上理解。学完泛函分析，才是近代数学的起跑点。

二、能量基本概念

2.1 能量的一般概念

        能量这个东西较为抽象，有了数学表达，才显得具体，比如：

        1）动能：

        在物理上，基本的能量公式为：，号称动能。其中m是质量，v是速度，而且。

        2）弹簧势能：

        弹簧的势能公式：,k是弹簧的常数，是伸长量。

        3）电流能量，是电流能量，在谱分解原理中，功率谱也是信号的平方。

        总之，从上述可以总结出：

        1）能量是一个平方函数。平方函数总是有最小值（或最大值），这是一个普遍规律。

        2）对函数的曲线用弹簧能量函数，长度的平方构成能量函数。

2.2 信号的能量

        然而在数学上，既无质量概念、又无时间的概念，因此，定义方法是：

•         1）定义原点能量总是0
•         2）坐标系内任意一个点的能量，是该点到原点距离的平方。

        因此能量的概念变成：

                

        此处告诉我们，长度（距离）具有能量的某些特征。因而更简化公式是：

                

        长度的平方就是能量。也就是，信号能量的函数是个抛物函数，就是这与物理上能量的定义是一致的。

三、勾股定律和能量守恒

        在直角坐标系中，存在“勾股定律”，从能量角度上说，一定长度构成的能量，可以分解到正交坐标系中，能量不会丢失。比如：

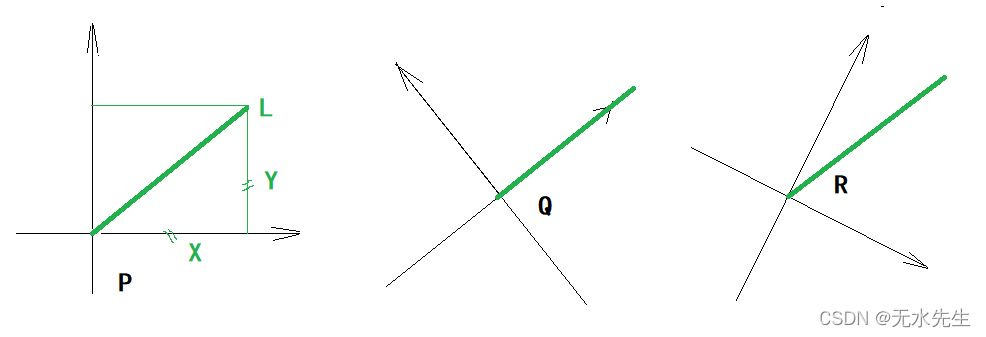
线段L在可以在任意直角坐标P、Q、R表示，坐标值可能变了，但L能量不变。 且恒有

         定理：信号在同维度正交坐标系下表示，其能量是守恒的。

        因此，信号在坐标转换中，只要坐标是正交的，那么，信号能量不会损失；反变换也能回到初始信号状态。关于正交投影，将在专题中论述。

四、 能量和欧式距离

对于任意两个点的距离是：

由于d是一个线段，那么就是两点之能量。

因此，给定任意两个点，其距离的平方，就是两点之能量。

五、圆周上的能量守恒

 用直角坐标系表示圆周L和K，如图：

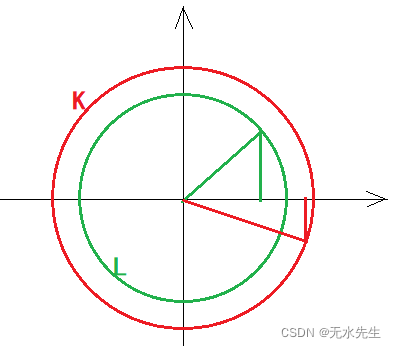
 由于L上任意一点都有如下属性：

因此，绿色圆上的所有点相对原点的能量全部是,处于等能量状态。同样，在红色圆K上，其上任意点也处于等能量态。这也不奇怪，因为恰好是函数的一条等高线。

六、方差和能量

给定一组坐标问这些点到哪个点的总能量最低？

也就是说，以某点为基点，所有点到该点的能量总和为最小。

于是：以为自变量的极值问题。

化简于是：,这就是所有点的平均么！

同理，

因此所有点的期望值（平均）；恰好是到所有点的能量最低的点。

 因而，对于这个统计问题，能量、方差、期望，在冥冥之中，存在以上的内在关系。

除此之外，还有线代的关系、柯西不等式，距离空间、傅里叶变换等，都是相关的话题，留着，以后慢慢展现。