此处介绍的剪枝算法属于后剪枝，即在决策树构建之后，在其基础上通过递归迭代等方式确定剪枝的节点。
其逻辑很朴素，即考虑某节点删除前后的错误率增加多少，选择对应节点错误率增加小的即可，此处衡量指标可以自定义为其他的指标，其过程都一样，只是当计算到对应节点时其保证此节点“有效力”的衡量指标的计算方式不同而已。

代价复杂度剪枝介绍

代价复杂度剪枝方法在1984年Breiman的经典CART算法中首次提到并使用，是一种后剪枝方法。
假设对于一棵CART决策树，R(T)是决策树误差（代价)，f(T)是一个返回树T的叶子集合的函数。
α是一个正则化参数，表示两者的平衡系数，其值越大，树越小，反之树越大。
一棵树的好坏用下式衡量：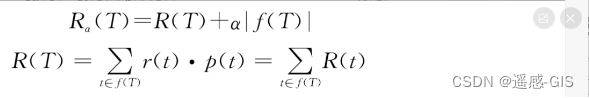

其中，${\sum }_{t\in f(T)}R(t)$ 表示每个叶子节点所产生的错误分类的误差之和，$p(t)=\frac{n(t)}{n}$，n（t）表示叶子节点t所处理的样本记录数，n表示总的样本记录数。 $r(t)=1-ma{x}_{k}p(C_k-t)$ 表示误分类比例。
结合上面公式可得：

其核心思想比较简单：

主要是递归到相应的节点，计算删除此节点之后的所有分支后，此节点作为叶节点后计算其样本的错误个数(此节点作为叶节点后，所有根据上一层落入此节点的数据是根据最多类别对应的标签来预测其他数据的，错误率等衡量指标，这里是选择错误个数，因为样本数是确定的，所有可不用计算错误率)，然后计算不删除之后的分支时，即原始树计算的错误率，然后结合两个计算结果，计算出误差增加率，选择误差增加最小的节点作为剪枝点。

但是是否是一次剪枝就得到最优结果呢？
答案是不一定的，可以在上次剪枝的基础上继续剪枝直到某种自定义的停止条件，比如节点个数等。
如果进行了多次剪枝，如何确定哪次最优呢？
可以采用交叉验证，如k折交叉验证等，选择准确率等衡量指标表现最优的哪次即可。
所以ccp的整个剪枝流程就是：

1. 先根据数据集构建原始树
2. 依次对每个节点进行计算：

计算数据集在原始树下的错误率；
计算当此节点作为叶节点的错误率，即落入此节点的预测标签为此节点中类别最多所有对应的标签；
上述相减，除以此节点之后分支的节点数量(对应公式中的f(t)，计算出"平均节点错误增加率"

3. 计算出所有节点的平均错误增加率之后，进行对比，选择错误增加最小的对应的节点即为目标节点即可
4. 可考虑重复多次剪枝，最后用交叉验证选择最优即可

整个过程用递归，迭代即可完成，是思想就是将此节点剪枝前后的错误率增加是大还是小的问题，选择小的。
过程图如下所示。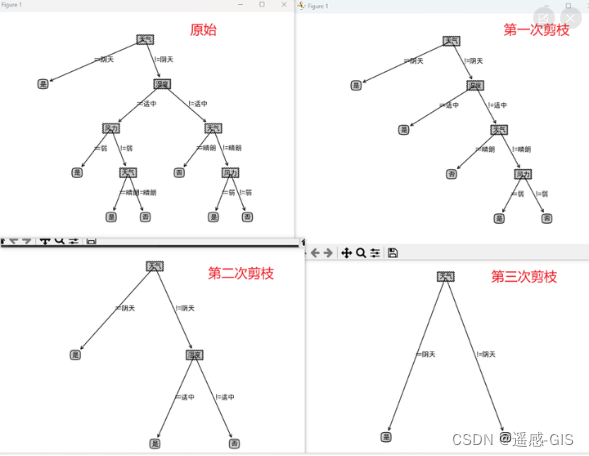

总结

书中代码细节比较繁琐，了解其思想即可，主要就是递归和迭代的熟练使用。
如果对具体的详细示例有兴趣，可以参考本专栏的参考书目：
<现代决策树模型及其编程实践：从传统决策树到深度决策树 黄智濒>
其电子书和其相关的源码可通过私信咨询获取。资源获取
欢迎点赞，收藏，关注，支持小生，打造一个好的遥感领域知识分享专栏。
同时欢迎私信咨询讨论学习，咨询讨论的方向不限于：地物分类/语义分割(如水体，云，建筑物，耕地，冬小麦等各种地物类型的提取）,变化检测,夜光遥感数据处理，目标检测，图像处理(几何矫正，辐射矫正(大气校正)，图像去噪等)，遥感时空融合，定量遥感（土壤盐渍化/水质参数反演/气溶胶反演/森林参数(生物量，植被覆盖度，植被生产力等)/地表温度/地表反射率等反演）以及高光谱数据处理等领域以及深度学习，机器学习等技术算法讨论，以及相关实验指导/论文指导等多方
面。遥感专栏

参考
【1】决策树的剪枝：CPP[代价复杂度剪枝]
【2】决策树CART 代价复杂度剪枝_最小代价复杂度-CSDN博客