嵌入式硬件基础

1. 嵌入式微处理器结构

考点分析：冯·诺依曼结构和哈弗结构

• 冯·诺依曼结构：是一种将程序指令存储器和数据存储器合并在一起的存储器结构
  
• 哈弗结构：是一种将程序指令存储和数据存储分开的存储器结构
  

2. 计算机硬件组成

考点分析：计算机硬件组成，运算器和控制器，及其内部寄存器的作用

2.1 基本的计算机硬件系统

硬件系统由运算器、控制器、存储器、输入设备、输出设备五大部分组成

• CPU：由运算器 +控制器 +寄存器组 +内部总线 组成
• 主机：由CPU + 主存储器 组成
• 存储器：分为内部存储和外部存储
• 外设：输入设备和输出设备合并称为外设

2.2 运算器

运算器的功能：执行所有的算术运算以及逻辑运算
运算器的组成:

– 算术逻辑单元：ALU 实现对数据的算术和逻辑运算
– 累加寄存器：AC 运算结果或源操作数的存放区
– 数据缓冲寄存器：DR 暂时存放内存的指令或数据
– 状态条件寄存器：PSW 保存指令运行结果的条件码内容

2.3 控制器

控制器的功能：控制整个CPU的工作
控制器的组成：

– 指令寄存器：IR 暂存CPU执行指令
– 程序计数器：PC 存放指令执行地址
– 地址寄存器：AR 保存当前CPU所访问的内存地址
– 指令译码器：ID 分析指令操作码

3. 数据的表示

考点分析：二、十、十六进制之间的整数及小数的互相转换，计算机中数的表示和范围，浮点数的表示，算数运算，逻辑运算， 短路计算

3.1 进制的转换

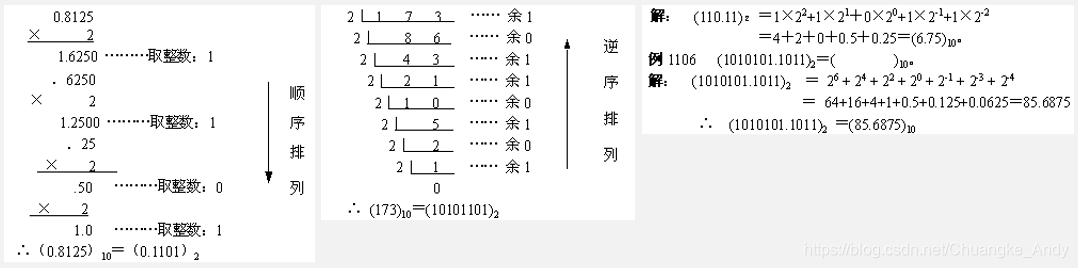
• R进制整数转十进制：位权展开法

• 十进制整数转R进制：除以R倒取余数法

• 十进制小数转R进制：乘以R正取整数法

• m进制转n进制：除了以下两种进制间可直接转化，其他的都要通过十进制中转转化

– 二进制转八进制：421法
– 二进制转十六进制：8421法

3.2 数的表示

各数值在计算机中的表示形式称为机器数，机器数是使用二进制，有无符号数和有符号数之分，数的符号用0（正数）和1（负数）表示，小数点隐含不显示

为了简化计算机对于减法的处理，带符号数规定了以下编码方式：

• 原码：最高位表示符号位，其他位存放该数的二进制绝对值
• 反码：正数的反码即原码，负数的反码是在其原码上按位取反（除符号位外）
• 补码：正数的补码即原码，负数的补码等于反码+1
• 移码：用作浮点运算的阶码，无论正负，将补码的符号位取反得到

3.3 定点数和浮点数

定点与浮点是指一个数的小数点位置是固定还是浮动

• 定点数：小数点位置人为约定固定不变，一般有定点纯小数和定点纯整数两种

• 浮点数：小数点的位置是浮动的，由尾数与阶数两部分组成

浮点格式表示一个二进制数N的形式为： N = F × 2^E
其中 E 称为阶码（含符号的纯整数）；F 叫做尾数（含符号的纯小数）
例如：二进制 101.011 = 0.101011 × 2³； -101.011 = 1.101011 × 2³

3.4 算术和逻辑运算

运算符优先级记忆口诀：单算移关与，异或逻条赋

4. 校验码

考点分析：奇偶校验码，循环冗余校验码，海明校验码

4.1 奇偶校验码

奇偶校验码是一种简单的检错码，其编码规则是先将所要传输的数据码元分组，在分组数据后面附加一位监督位，使该组码连同监督位在内的码组中的“1”的个数为偶数（称为偶校验）或奇数（称为奇校验），在接收端按同样的规律检查，如发现不符就说明产生了差错，但是不能确定差错的具体位置，即不能纠错

奇偶校验码的这种监督关系可用公式表示，设码组长度为n，表示为（a_n-1, a_n-2, a_n-3,…, a₀）,其中前n-1位为信息码元，第n位为监督位a₀ （⊕表示模2和，等价于异或运算）

• 偶校验时，a₀⊕a₁⊕…⊕a_n-1 = 0,即监督位a₀ = a₁⊕…⊕a_n-1
• 奇校验时，a₀⊕a₁⊕…⊕a_n-1 = 1,即监督位a₀ = a₁⊕…⊕a_n-1⊕1

例如：信息码1110011000按照偶监督规则插入监督位应为a₀ = 1⊕1⊕1⊕0⊕0⊕1⊕1⊕0⊕0⊕0 =1

4.2 循环冗余校验码（CRC）

CRC的编码方法：

• 将x的最高次幂为r的生成多项式g(x)转换成对应的r+1位二进制数码组
• 将信息码左移r位，相当于对应的信息多项式C(x) * 2^r
• 用二进制数对信息码做模2除 （异或 ），得到r位余数即FCS
• 将余数拼到信息码左移后空出的位置，得到完整的CRC码

如生成多项式A(x) = x⁵ + x⁴ + x² + 1，可转换为二进制码组 110101
生成多项式是接收端和发送端的约定，对应一个二进制数，在传输过程中这个数保持不变

FCS帧检验列：将信息位后添加的r位校验码，称为信息的FCS帧检验列

4.3 海明校验码

海明校验码本质也是使用奇偶校验方式来检验。信息位数k与校验位数r之间要满足公式：2^r ≥ k + r + 1

推导并使用信息长度为k位的码字的海明码，需要如下步骤：

• 确定最小的校验位数r，将他们记成P₁、P₂、…P_r，每个校验位符合不同的奇偶测试规定
• 原有信息和r个校验位一起编成长为 k+r 位的新码字。选择校验位奇校验还是偶校验（0或1）
• 对所接收的信息作所需的 r 个奇偶检查
• 若所有的奇偶检查结果均为正确，则认为信息无错误；若发现有错误，则错误的位由这些检查的结果来唯一地确定

习惯上校验位被安排在1、2、4、8…（即2⁰、2¹、2²、2³、…）的位置上。当k = 4，r = 3时，信息位与校验位的分布情况如下表所示

r 个校验位是通过对 k+r 位复合码字进行奇偶校验而确定的

• P₁负责校验海明码的第1、 3、 5、 7…（从P₁开始取一位，再每间隔一位取一位…）
• P₂负责校验海明码的第2、 3、 6、 7…（从P₂开始取两位，再每间隔二位取二位…）
• P₃负责校验海明码的第4、 5、 6、 7…（从P₃开始取四位，再每间隔四位取四位…）

对k = 4，r = 3的码字进行海明码编码，校验位采用偶校验，则需r = 3次偶校验。这里3次检查分别以R₁、R₂、R₃表示，见下表示

可得到三个方程式即确定校验位的三个公式：

R₁ = B₁⊕B₃⊕B₅⊕B₇ = 0 得 P₁ = D₁⊕D₂⊕D₄
R₂ = B₂⊕B₃⊕B₆⊕B₇ = 0 得 P₂ = D₁⊕D₃⊕D₄
R₃ = B₄⊕B₅⊕B₆⊕B₇ = 0 得 P₃ = D₂⊕D₃⊕D₄

例：若有四位信息码1011，求3个校验位P₁、P₂、P₃值并生成海明码编码，根据以上介绍可算出

以上是发送方的处理过程，在接收方也可以根据这3个校验方程对接收到的信息进行同样的奇偶校验测试：

A = B₁⊕B₃⊕B₅⊕B₇ = 0
B = B₂⊕B₃⊕B₆⊕B₇ = 0
C = B₄⊕B₅⊕B₆⊕B₇ = 0

若三个检验方程都成立，则说明没有错；若不成立即方程式右边不等于0，说明有错。从3个方程式右边的值，可以判断出哪一位出错