【机器学习基础】系列博客为参考周志华老师的《机器学习》一书，自己所做的读书笔记。

1.核函数

在之前的博客中，我们假设训练样本是线性可分的，即存在一个划分超平面能将训练样本正确分类。然而在现实任务中，原始样本空间内也许并不存在一个能正确划分两类样本的超平面。例如下图中的“异或”问题就不是线性可分的：

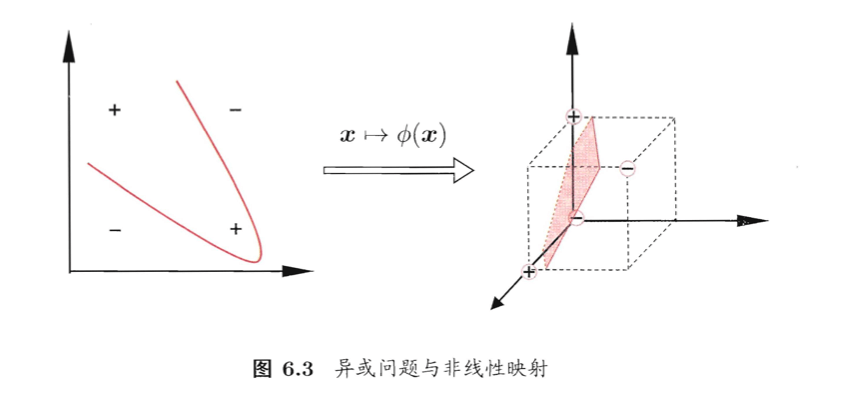
对这样的问题，可将样本从原始空间映射到一个更高维的特征空间，使得样本在这个特征空间内线性可分。例如在上图中，若将原始的二维空间映射到一个合适的三维空间，就能找到一个合适的划分超平面。⚠️幸运的是，如果原始空间是有限维，即属性数有限，那么一定存在一个高维特征空间使样本可分。

令$\varphi (\mathbf{x})$表示将$\mathbf{x}$映射后的特征向量，于是，在特征空间中划分超平面所对应的模型可表示为：

$$f(\mathbf{x})={\mathbf{w}}^T\varphi (\mathbf{x})+b\text{\hspace{1em}(1)}$$

其中$\mathbf{w},b$是模型参数，类似【机器学习基础】第十六课：支持向量机之间隔与支持向量中学到的SVM的基本型，有：

其对偶问题是：

求解式(3)涉及到计算$\varphi ({\mathbf{x}}_i{)}^T\varphi ({\mathbf{x}}_j)$，这是样本${\mathbf{x}}_i$与${\mathbf{x}}_j$映射到特征空间之后的内积。由于特征空间维数可能很高，甚至可能是无穷维，因此直接计算$\varphi ({\mathbf{x}}_i{)}^T\varphi ({\mathbf{x}}_j)$通常是困难的。为了避开这个障碍，可以设想这样一个函数：

$$\kappa ({\mathbf{x}}_i,{\mathbf{x}}_j)=<\varphi ({\mathbf{x}}_i{)}^T,\varphi ({\mathbf{x}}_j)>=\varphi ({\mathbf{x}}_i{)}^T\varphi ({\mathbf{x}}_j)\text{\hspace{1em}(4)}$$

即${\mathbf{x}}_i$与${\mathbf{x}}_j$在特征空间的内积等于它们在原始样本空间中通过函数$\kappa (\cdot ,\cdot )$计算的结果。有了这样的函数，我们就不必直接去计算高维甚至无穷维特征空间中的内积，于是式(3)可重写为：

求解后即可得到：

$$\begin{array}{rl}f(\mathbf{x})& ={\mathbf{w}}^T\varphi (\mathbf{x})+b\\ & =\sum _{i=1}^m{\alpha }_i{y}_i\varphi ({\mathbf{x}}_i{)}^T\varphi (\mathbf{x})+b\\ & =\sum _{i=1}^m{\alpha }_i{y}_i\kappa (\mathbf{x},{\mathbf{x}}_i)+b\end{array}\text{\hspace{1em}(6)}$$

这里的函数$\kappa (\cdot ,\cdot )$就是 “核函数(kernel function)” 。式(6)显示出模型最优解可通过训练样本的核函数展开，这一展式亦称 “支持向量展式(support vector expansion)”。

显然，若已知合适映射$\varphi (\cdot )$的具体形式，则可写出核函数$\kappa (\cdot ,\cdot )$。但在现实任务中我们通常不知道$\varphi (\cdot )$是什么形式，那么，合适的核函数是否一定存在呢？什么样的函数能做核函数呢？我们有下面的定理：

核函数定理： 令$\chi$为输入空间，$\kappa (\cdot ,\cdot )$是定义在$\chi \times \chi$上的对称函数，则$\kappa$是核函数当且仅当对于任意数据 D = { x 1 , x 2 , . . . , x m } D=\{\mathbf x_1,\mathbf x_2,...,\mathbf x_m \} D={x1​,x2​,...,xm​}，“核矩阵”(kernel matrix)$K$ 总是半正定的：

$$\mathbf{K}=\left[\begin{array}{ccccc}\kappa ({\mathbf{x}}_1,{\mathbf{x}}_1)& \cdots & \kappa ({\mathbf{x}}_1,{\mathbf{x}}_j)& \cdots & \kappa ({\mathbf{x}}_1,{\mathbf{x}}_m)\\ ⋮& \ddots & ⋮& \ddots & ⋮\\ \kappa ({\mathbf{x}}_i,{\mathbf{x}}_1)& \cdots & \kappa ({\mathbf{x}}_i,{\mathbf{x}}_j)& \cdots & \kappa ({\mathbf{x}}_i,{\mathbf{x}}_m)\\ ⋮& \ddots & ⋮& \ddots & ⋮\\ \kappa ({\mathbf{x}}_m,{\mathbf{x}}_1)& \cdots & \kappa ({\mathbf{x}}_m,{\mathbf{x}}_j)& \cdots & \kappa ({\mathbf{x}}_m,{\mathbf{x}}_m)\end{array}\right]$$

上述定理表明，只要一个对称函数所对应的核矩阵半正定，它就能作为核函数使用。事实上，对于一个半正定核矩阵，总能找到一个与之对应的映射$\varphi$。换言之，任何一个核函数都隐式地定义了一个称为 “再生核希尔伯特空间”(Reproducing Kernel Hilbert Space，简称RKHS) 的特征空间。

通过前面的讨论可知，我们希望样本在特征空间内线性可分，因此特征空间的好坏对支持向量机的性能至关重要。需注意的是，在不知道特征映射的形式时，我们并不知道什么样的核函数是合适的，而核函数也仅是隐式地定义了这个特征空间。

⚠️于是，“核函数选择”成为支持向量机的最大变数。若核函数选择不合适，则意味着将样本映射到了一个不合适的特征空间，很可能导致性能不佳。

这方面有一些基本的经验，例如对文本数据通常采用线性核，情况不明时可先尝试高斯核。

常用的核函数：

$d=1$时退化为线性核，高斯核亦称RBF核。

此外，还可通过函数组合得到，例如：

👉若${\kappa }_1$和${\kappa }_2$为核函数，则对于任意正数${\gamma }_1,{\gamma }_2$，其线性组合

$${\gamma }_1{\kappa }_1+{\gamma }_2{\kappa }_2$$

也是核函数。

👉若${\kappa }_1$和${\kappa }_2$为核函数，则核函数的直积

$${\kappa }_1\otimes {\kappa }_2(\mathbf{x},\mathbf{z})={\kappa }_1(\mathbf{x},\mathbf{z}){\kappa }_2(\mathbf{x},\mathbf{z})$$

也是核函数。

👉若${\kappa }_1$为核函数，则对于任意函数$g(\mathbf{x})$，

$$\kappa (\mathbf{x},\mathbf{z})=g(\mathbf{x}){\kappa }_1(\mathbf{x},\mathbf{z})g(\mathbf{z})$$

也是核函数。

2.直积

“直积” 又称 “笛卡尔乘积”：表示为$X\otimes Y$，第一个对象是$X$的成员而第二个对象是$Y$的所有可能有序对的其中一个成员。

例如， A = { a , b } , B = { 0 , 1 , 2 } A=\{a,b \},B=\{ 0,1,2 \} A={a,b},B={0,1,2}，则：

$$A\otimes B=\{(a,0),(a,1),(a,2),(b,0),(b,1),(b,2)\}$$

$$B\otimes A=\{(0,a),(0,b),(1,a),(1,b),(2,a),(2,b)\}$$

---

想要获取最新文章推送或者私聊谈人生，请关注我的个人微信公众号：⬇️x-jeff的AI工坊⬇️

个人博客网站：https://shichaoxin.com

GitHub：https://github.com/x-jeff

---