1 人工神经网络

人工神经网络（Artificial Neural Networks, ANN）是模拟生物神经元结构的计算模型，它模仿了大脑处理信息的基本方式。人工神经网络是由大量的简单处理单元——即“神经元”——组成的网络，这些神经元通过连接权重进行交互，并能够对输入数据进行复杂的非线性变换。

1.1 工作原理

人工神经网络通过调整连接权重来学习数据中的模式。这个过程通常涉及以下几个步骤：

1. 前向传播：输入数据通过网络向前传递，从输入层到输出层，经过一系列的加权和激活操作。
2. 损失计算：输出层产生的结果与实际目标进行比较，得到一个误差度量，称为损失函数。
3. 反向传播：通过计算损失函数相对于每个权重的梯度，然后根据这个梯度调整权重，以减小损失。
4. 优化算法：如梯度下降等方法用于更新权重，目的是最小化损失函数。

1.2 人工神经网络的组成

1. 神经元（Neuron）：是神经网络的基本单元，类似于生物神经元的结构。
2. 输入层（Input Layer）：接收外部输入数据。
3. 隐藏层（Hidden Layer）：一个或多个，负责处理输入层传来的数据，并进行非线性变换。
4. 输出层（Output Layer）：输出最终结果。

1.3 数学原理

1. 权重（Weight）：每个神经元之间的连接都有一个权重，表示连接的强度。
2. 偏置（Bias）：每个神经元都有一个偏置，用于调整输出值。
3. 激活函数（Activation Function）：用于引入非线性因素，常见的激活函数有Sigmoid、ReLU等。
   以下是神经网络的基本数学原理：

1.3.1 前向传播（Forward Propagation）

单个神经元示意图：

对于一个简单的神经元，其输出计算公式为：
$$a=\sigma (\sum _{i=1}^n{w}_i{x}_i+b)$$
其中：

• $a$：神经元的输出
• $\sigma$：激活函数
• $w_i$：第$i$个输入的权重
• $x_i$：第$i$个输入
• $b$：偏置
  对于多层神经网络，前向传播的过程可以表示为：
  $$z^{[l]}=W^{[l]}{a}^{[l-1]}+b^{[l]}$$
  $$a^{[l]}=\sigma (z^{[l]})$$
  其中：
• $z^{[l]}$：第$l$层的线性组合
• $W^{[l]}$：第$l$层的权重矩阵
• $a^{[l-1]}$：第$l-1$层的输出
• $b^{[l]}$：第$l$层的偏置
• $a^{[l]}$：第$l$层的输出

1.3.2 激活函数示例

Sigmoid函数：
$$\sigma (z)=\frac{1}{1+e^{-z}}$$
ReLU函数：
$$\text{ReLU}(z)=\max (0,z)$$

1.4 简单示例

假设我们有一个简单的神经网络，只有一个输入层、一个隐藏层和一个输出层。输入层有一个神经元，隐藏层有两个神经元，输出层有一个神经元。激活函数使用Sigmoid。

输入层到隐藏层的计算

设输入为$x$，隐藏层两个神经元的权重分别为$w_1$和$w_2$，偏置分别为$b_1$和$b_2$，则隐藏层的输出为：
$$z_1=w_{1}x+b_1$$
$$a_1=\sigma (z_1)$$
$$z_2=w_{2}x+b_2$$
$$a_2=\sigma (z_2)$$

隐藏层到输出层的计算

设隐藏层到输出层的权重分别为$v_1$和$v_2$，偏置为$c$，则输出层的输出为：
$$z_{\text{out}}=v_1{a}_1+v_2{a}_2+c$$
$$a_{\text{out}}=\sigma (z_{\text{out}})$$
这就是一个简单的人工神经网络的数学原理和计算过程。在实际应用中，神经网络的结构和参数需要通过训练数据来学习得到。
如图：

由上图我们约定以下表示。a1、a2、h1、h2…代表神经元的名字。
$a{1}_i$代表a1神经元的输入，$a{1}_o$代表a1神经元的输出。
a1与a2代表输入层，通常情况下输入层通常不包含权重和激活函数，它仅仅接收数据。
2与3是当前神经网络的输入。当2输入到a1神经元后即$a{1}_i=2$，由于a1是输入层神经元，从而变成$$a{1}_o=a{1}_i=2$$
当3输入到神经元后，同理，从而变成$$a{2}_o=a{2}_i=3$$
此时神经元分别输出$a{1}_o$ 、$a{2}_o$。
从图中我们可以看出，$a{1}_o$ 、$a{2}_o$首先会作为隐藏层（中间那一列的神经元）的输入。
对于隐藏层神经元我们可以得到
$h{1}_i=a{1}_o\ast 1+a{2}_o\ast 2$
$h{1}_o=\sigma (h{1}_i+b)$
$h{2}_i=a{1}_o\ast 2+a{2}_o\ast 3$
$h{2}_o=\sigma ((h{2}_i+b)+b)$
…
注意
在通常情况下，输入层通常不包含权重和激活函数，它的主要功能是接收外部输入数据并将其传递给网络的下一层次，即隐藏层。输入层的节点（或称为神经元）只是简单地持有输入数据的值，并没有进行任何计算或变换。
思考
1、你可以把其它几个神经元的输入输出写出来了吗？
2、我们如何用计算机能看懂的方式去实现计算呢？

输入层定义

给定输入向量 $\mathbf{x}=[x_1,x_2]=[2,3]$。

隐藏层权重与偏置

隐藏层到输出层的权重矩阵定义为：
$${\mathbf{W}}_{\text{hidden}}=\left[\begin{array}{cc}1& 2\\ 2& 3\\ 1& 1\\ 3& 1\end{array}\right]$$
假设每个隐藏层神经元的偏置都是 $0.2$，则偏置向量为：
$${\mathbf{b}}_{\text{hidden}}=\left[\begin{array}{c}0.2\\ 0.2\\ 0.2\\ 0.2\end{array}\right]$$

计算隐藏层的输入

隐藏层每个神经元的输入计算如下：
$${\mathbf{z}}_{\text{hidden}}={\mathbf{W}}_{\text{hidden}}\cdot \mathbf{x}+{\mathbf{b}}_{\text{hidden}}$$
具体计算过程如下：
$${\mathbf{z}}_{\text{hidden}}=\left[\begin{array}{cc}1& 2\\ 2& 3\\ 1& 1\\ 3& 1\end{array}\right]\cdot \left[\begin{array}{c}2\\ 3\end{array}\right]+\left[\begin{array}{c}0.2\\ 0.2\\ 0.2\\ 0.2\end{array}\right]$$
$${\mathbf{z}}_{\text{hidden}}=\left[\begin{array}{c}1\cdot 2+2\cdot 3\\ 2\cdot 2+3\cdot 3\\ 1\cdot 2+1\cdot 3\\ 3\cdot 2+1\cdot 3\end{array}\right]+\left[\begin{array}{c}0.2\\ 0.2\\ 0.2\\ 0.2\end{array}\right]$$
$${\mathbf{z}}_{\text{hidden}}=\left[\begin{array}{c}2+6\\ 4+9\\ 2+3\\ 6+3\end{array}\right]+\left[\begin{array}{c}0.2\\ 0.2\\ 0.2\\ 0.2\end{array}\right]$$
$${\mathbf{z}}_{\text{hidden}}=\left[\begin{array}{c}8.2\\ 13.2\\ 5.2\\ 9.2\end{array}\right]$$

应用激活函数

隐藏层的输出使用sigmoid函数：
$${\mathbf{a}}_{\text{hidden}}=\sigma ({\mathbf{z}}_{\text{hidden}})=\frac{1}{1+e^{-{\mathbf{z}}_{\text{hidden}}}}$$
对于每个元素 $z_i$：
$$\sigma (8.2)\approx 0.9997,\sigma (13.2)\approx 0.9999,\sigma (5.2)\approx 0.9933,\sigma (9.2)\approx 0.9998$$
因此：
$${\mathbf{a}}_{\text{hidden}}\approx \left[\begin{array}{c}0.9997\\ 0.9999\\ 0.9933\\ 0.9998\end{array}\right]$$

输出层的输入

输出层到隐藏层的权重矩阵定义为：
$${\mathbf{W}}_{\text{output}}=\left[\begin{array}{cccc}1& 1& 1& 1\\ 1& 0& 0& 1\end{array}\right]$$

输出层的偏置向量假设为：
$${\mathbf{b}}_{\text{output}}=\left[\begin{array}{c}0.2\\ 0.2\end{array}\right]$$

输出层的输出计算如下：
$${\mathbf{z}}_{\text{output}}=\sigma ({\mathbf{W}}_{\text{output}}\cdot {\mathbf{a}}_{\text{hidden}}+{\mathbf{b}}_{\text{output}})$$
接下来，您可以根据这些步骤计算输出层的输入和最终的输出。

练习：

计算上图中的y1与y2。

2 梯度下降法

#2.1 梯度下降法的数据基础

梯度下降法是一种更新神经网络参数的算法，该算法是一种迭代算法，其目的是找到函数的最优值。梯度指的函数在某点处沿着其方向导数的方向所取得的最大值。
梯度是一个矢量，梯度的值表示函数在此点的最大斜率或变化率，梯度的总体方向表示函数在此点的变化方向。梯度下降法的优化过程是沿着函数的梯度寻找最优值。
当然可以。梯度是数学分析中的一个基本概念，特别是在向量分析和优化问题中。以下是梯度的定义和关键点：

1. 定义：梯度是一个多变量函数在其定义域内的某一点处变化最快的方向，以及在该方向上的变化率。
2. 数学表示：对于实值函数 $f(\mathbf{x})$，其中 $\mathbf{x}=[x_1,x_2,\dots ,x_n]$ 是一个包含 $n$ 个变量的向量，梯度通常表示为 $\nabla f(\mathbf{x})$ 或 ${\partial }_{i}f(\mathbf{x})$，并定义为：
   $$\nabla f(\mathbf{x})=\left[\frac{\partial f}{\partial x_1},\frac{\partial f}{\partial x_2},\dots ,\frac{\partial f}{\partial x_n}\right]$$
   这里，$\frac{\partial f}{\partial x_i}$ 是函数 $f$ 对变量 $x_i$ 的偏导数。
3. 向量性质：梯度是一个向量，其分量是函数对各个变量的偏导数，因此梯度的方向指示了函数增长最快的方向，其大小（模长）表示在该方向上的增长率。
4. 几何意义：在三维空间中，如果将梯度向量 $\nabla f(\mathbf{x})$ 放在点 $\mathbf{x}$ 上，则该向量垂直于函数 $f$ 在该点的等高线（或等值面），并且指向函数值增加最快的方向。
5. 应用：
   • 优化：在优化问题中，梯度下降法利用梯度的信息来找到函数的局部最小值。算法通过沿着梯度的反方向更新变量，以减少函数的值。
   • 物理：在物理学中，梯度可以表示物理量的空间变化率，如温度或电势。
6. 特殊情况：对于单变量函数，梯度简化为该函数的导数，并且是一个标量而不是向量。
   总结来说，梯度是一个多变量函数在特定点上关于各个变量的偏导数构成的向量，它描述了函数在该点处最大增长的方向和增长的速度。

自变量如何变化，才能使得应变量快速地变成最小值？？？？？？

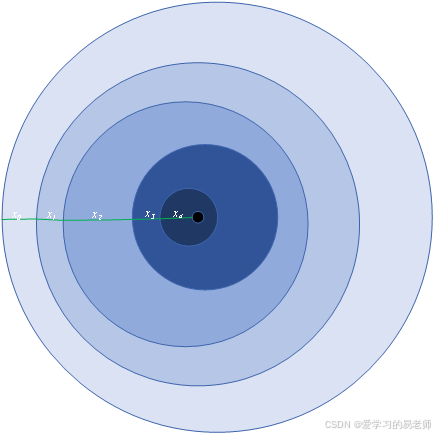
图2中每一次下降的移动方向都与出发点垂直。
现有函数，第$k$次的迭代值记为$f(x_k)$，迭代$k$次后最优值表示为$x^{\ast }$。对于在$x$的梯度如公式所示。

$$\nabla f(x)$$

在函数仅有一阶导数时。
若存在多个自变量如$x_1,x_2,...,x_n$，则梯度公式如公式所示。

$$\nabla f(x)=\left(\frac{\partial f}{\partial x_1},\frac{\partial f}{\partial x_2},...,\frac{\partial f}{\partial x_n}\right)$$

对于第$k$次迭代值如公式所示。

$$x_{k+1}=x_k-\alpha \nabla f(x_k)$$

代表第$k$次的步长，$\alpha$是当前梯度。在梯度下降的情况下，$\alpha$的值为正数，且必须大于0。多次迭代的目的是使得公式成立。

$$f(x^{\ast })=\underset{x}{\min }f(x)$$

2.2 神经网络的梯度下降法

梯度下降法常用于神经网络的参数更新，设神经网络的权值参数为$w$，是一个该神经网络所有参数的集合。往神经网络输入数据后，输入数据与神经网络的参数进行矩阵运算得出结果，如公式所示。

$$\hat{y}=f_w(x)$$

是神经网络模型，$X$是所以输入数据的集合，通常是一个矩阵，X可以是多条数据的集合。当得出预测值后需要求该预测值与标签值的误差，即存在误差函数如公式(2.19)所示。

$$L(\hat{y},y)=\frac{1}{2}(\hat{y}-y{)}^2$$

函数显示了预测值与标签值的差距，此时需要调整神经网络的$w$，使得值最小。这一步可以用2.2.1小节所示的梯度下降法更新参数以求得最小值。此时需要将公式(2.19)中的$w$作为自变量，$X,y$作为固定值。如公式(2.20)所示。

$${\nabla }_{w}L(\hat{y},y)$$

则根据梯度下降法，参数的更新公式如公式（2.21）所示。

$$w\leftarrow w-\alpha {\nabla }_{w}L(\hat{y},y)$$

2.2.3 数学计算示例

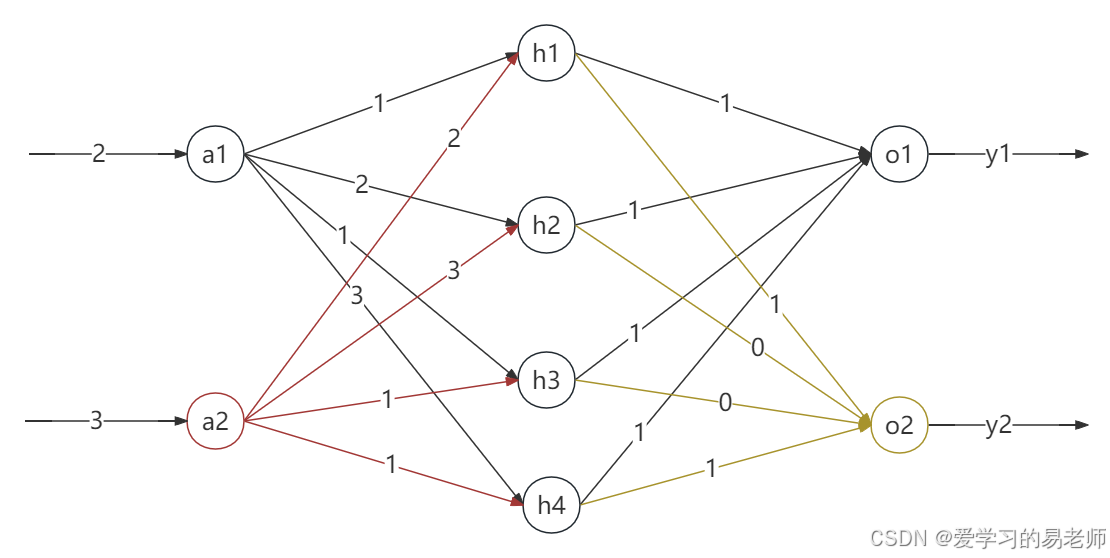
以本图为例：
假设:
激活函数为 $f(x+b)=2(x+0)=2x$
损失函数为 $f(y_t,y_m)=\frac{1}{2}(y_t-y_m{)}^2$
$y_t$代表标签，$y_m$代表模型输出。

隐藏层到输出层的权重矩阵定义为：
$${\mathbf{W}}_{\text{hidden}}=\left[\begin{array}{cc}1& 2\\ 2& 3\\ 1& 1\\ 3& 1\end{array}\right]$$
输出层到隐藏层的权重矩阵定义为：
$${\mathbf{W}}_{\text{output}}=\left[\begin{array}{cccc}1& 1& 1& 1\\ 1& 0& 0& 1\end{array}\right]$$
偏置$bias=0$

输入 $x=[2,3]$ 标签为$y_t=[2,3]$

则计算过程为：
首先，我们需要根据给定的网络结构和参数计算模型的输出。这个过程涉及到前向传播。然后，我们将计算损失函数的梯度，并更新权重矩阵。这个过程称为反向传播。

前向传播

1. 计算隐藏层的输出:

   隐藏层的输出是由输入层通过隐藏层权重矩阵计算得到的。我们使用给定的激活函数 $f(x+b)=2x$。
   $$\mathbf{h}=f({\mathbf{W}}_{\text{hidden}}\cdot \mathbf{x}+\mathbf{b})=2({\mathbf{W}}_{\text{hidden}}\cdot \mathbf{x})$$
   其中 $\mathbf{x}=[2,3]$，$\mathbf{b}$ 是偏置，这里为0。

2. 计算输出层的输出:
   输出层的输出是由隐藏层通过输出层权重矩阵计算得到的。
   $${\mathbf{y}}_m={\mathbf{W}}_{\text{output}}\cdot \mathbf{h}$$
   接下来，我们将使用Python来计算这些值。

import numpy as np
#定义权重矩阵和输入
W_hidden = np.array([[1, 2], [2, 3], [1, 1], [3, 1]])
W_output = np.array([[1, 1, 1, 1], [1, 0, 0, 1]])
x = np.array([2, 3])
bias = 0
#计算隐藏层的输出
h = 2 * (W_hidden @ x)
#计算输出层的输出
y_m = W_output @ h
h, y_m

(array([16, 26, 10, 18]), array([70, 34]))

隐藏层的输出为 $[16,26,10,18]$，输出层的输出（模型输出）为 $[70,34]$。

反向传播

1. 计算损失函数的梯度:
   损失函数为 $f(y_t,y_m)=\frac{1}{2}(y_t-y_m{)}^2$。我们需要计算损失函数关于模型输出 $y_m$ 的梯度。
   $${\nabla }_{y_m}f(y_t,y_m)=y_m-y_t$$
2. 计算输出层权重的梯度:
   梯度是损失函数关于输出层权重矩阵的导数。
   $${\nabla }_{{\mathbf{W}}_{\text{output}}}f={\nabla }_{y_m}f(y_t,y_m)\cdot {\mathbf{h}}^T$$
3. 计算隐藏层权重的梯度:
   梯度是损失函数关于隐藏层权重矩阵的导数。
   $${\nabla }_{{\mathbf{W}}_{\text{hidden}}}f={\nabla }_{{\mathbf{W}}_{\text{output}}}f\cdot {\mathbf{W}}_{\text{output}}\cdot 2\cdot {\mathbf{x}}^T$$
4. 更新权重:
   使用梯度下降法更新权重。这里我们假设学习率为 $\eta$。
   $${\mathbf{W}}_{\text{output}}^{\prime }={\mathbf{W}}_{\text{output}}-\eta {\nabla }_{{\mathbf{W}}_{\text{output}}}f$$
   $${\mathbf{W}}_{\text{hidden}}^{\prime }={\mathbf{W}}_{\text{hidden}}-\eta {\nabla }_{{\mathbf{W}}_{\text{hidden}}}f$$
   接下来，我们将计算这些梯度，并假设学习率为0.01来更新权重。
   思考：一次性输入多条数据怎么办？？
   当时是求平均，求多条数据算出的梯度，然后求平均就是当前批次算出的梯度。

定义标签和学习率

$y_t=np.array([2,3])$
$eta=0.01$

1. 计算输出层的梯度：首先，我们计算损失函数关于输出层输出 $ y_m $ 的梯度。这是因为损失函数直接依赖于模型输出和真实标签。
   $${\nabla }_{y_m}f(y_t,y_m)=\frac{\partial f}{\partial y_m}=y_m-y_t$$

2. 传播梯度到输出层权重：然后，我们使用链式法则将这个梯度传播到输出层的权重。这涉及到计算损失函数关于每个输出层权重的偏导数。
   $${\nabla }_{{\mathbf{W}}_{\text{output}}}f=\frac{\partial f}{\partial {\mathbf{W}}_{\text{output}}}={\nabla }_{y_m}f(y_t,y_m)\cdot {\mathbf{h}}^T$$

   $${\mathbf{y}}_m={\mathbf{W}}_{\text{output}}\mathbf{h}$$
   根据链式法则，损失函数关于输出层权重 ${\mathbf{W}}_{\text{output}}$ 的梯度可以表示为：
   $${\nabla }_{{\mathbf{W}}_{\text{output}}}f=\frac{\partial f}{\partial {\mathbf{y}}_m}\cdot \frac{\partial {\mathbf{y}}_m}{\partial {\mathbf{W}}_{\text{output}}}$$
   我们已经计算了 $\frac{\partial f}{\partial {\mathbf{y}}_m}$，即 ${\nabla }_{y_m}f(y_t,y_m)$。接下来，我们需要计算 $\frac{\partial {\mathbf{y}}_m}{\partial {\mathbf{W}}_{\text{output}}}$。

3. 计算 $\frac{\partial {\mathbf{y}}_m}{\partial {\mathbf{W}}_{\text{output}}}$：由于 ${\mathbf{y}}_m={\mathbf{W}}_{\text{output}}\mathbf{h}$，我们可以得出：
   $$\frac{\partial {\mathbf{y}}_m}{\partial {\mathbf{W}}_{\text{output}}}={\mathbf{h}}^T$$
   之所以是 ${\mathbf{h}}^T$ 是因为矩阵乘的时候转置了。现在要求一一对应所有要转置回来。
   这是因为对于矩阵 ${\mathbf{W}}_{\text{output}}$ 中的每个元素 $w_{ij}$，${\mathbf{y}}_m$ 的第 $i$ 个元素是 $w_{ij}$ 和 $\mathbf{h}$ 的第$j$ 个元素的乘积之和。

4. 最终梯度：将这两个部分结合起来，我们得到：
   $${\nabla }_{{\mathbf{W}}_{\text{output}}}f=({\mathbf{y}}_m-{\mathbf{y}}_t)\cdot {\mathbf{h}}^T$$
   这就是损失函数关于输出层权重矩阵的梯度。通过这个梯度，我们可以更新输出层的权重，以减少损失函数的值。

5. 计算隐藏层的梯度：接下来，我们需要计算损失函数关于隐藏层输出的梯度，然后将这个梯度传播到隐藏层的权重。
   $${\nabla }_{\mathbf{h}}f=\frac{\partial f}{\partial \mathbf{h}}=\frac{\partial f}{\partial {\mathbf{y}}_m}\cdot \frac{\partial {\mathbf{y}}_m}{\partial \mathbf{h}}$$
   $${\nabla }_{\mathbf{h}}f=\frac{\partial f}{\partial \mathbf{h}}={\mathbf{W}}_{\text{output}}^T\cdot {\nabla }_{y_m}f(y_t,y_m)$$

6. 传播梯度到隐藏层权重：最后，我们将这个梯度传播到隐藏层的权重。
   $${\nabla }_{{\mathbf{W}}_{\text{hidden}}}f=\frac{\partial f}{\partial {\mathbf{W}}_{\text{hidden}}}={\nabla }_{\mathbf{h}}f\cdot {\mathbf{x}}^T$$

2.3 代码计算1

import numpy as np

# 定义权重矩阵、输入和标签
W_hidden = np.array([[1, 2], [2, 3], [1, 1], [3, 1]])
W_output = np.array([[1, 1, 1, 1], [1, 0, 0, 1]])
x = np.array([2, 3])
y_t = np.array([2, 3])
bias = 0
eta = 0.01  # 学习率

# 步骤 1: 前向传播
# 计算隐藏层输出
h = 2 * (W_hidden @ x)

# 计算输出层输出
y_m = W_output @ h

# 步骤 2: 反向传播
# 计算损失函数关于模型输出的梯度
grad_y_m = y_m - y_t

# 计算输出层权重的梯度
grad_W_output = grad_y_m[:, np.newaxis] * h[np.newaxis, :]

# 计算损失函数关于隐藏层输出的梯度
grad_h = W_output.T @ grad_y_m

# 计算隐藏层权重的梯度
grad_W_hidden = grad_h[:, np.newaxis] * x[np.newaxis, :]

# 步骤 3: 更新参数
W_output_new = W_output - eta * grad_W_output
W_hidden_new = W_hidden - eta * grad_W_hidden

# 输出：h, y_m, grad_y_m, grad_W_output, grad_h, grad_W_hidden, W_output_new, W_hidden_new)
print("h:", h)
print("y_m:", y_m)
print("grad_y_m:", grad_y_m)
print("grad_W_output:", grad_W_output)
print("grad_h:", grad_h)
print("grad_W_hidden:", grad_W_hidden)
print("W_output_new:", W_output_new)
print("W_hidden_new:", W_hidden_new)

2.4 基于深度学习框架的快速运算

PaddlePaddle

import paddle
from paddle import nn
from paddle.optimizer import SGD

# 定义模型
class SimpleNN(paddle.nn.Layer):
    def __init__(self):
        super(SimpleNN, self).__init__()
        self.hidden_layer = nn.Linear(2, 4, bias_attr=False)
        self.output_layer = nn.Linear(4, 2, bias_attr=False)
        self.activation = nn.ReLU()

    def forward(self, x):
        x = self.hidden_layer(x)
        x = self.activation(x)
        x = self.output_layer(x)
        return x

# 实例化模型
model = SimpleNN()

# 设置参数（权重）
model.hidden_layer.weight.set_value(paddle.to_tensor([[1, 2], [2, 3], [1, 1], [3, 1]], stop_gradient=False))
model.output_layer.weight.set_value(paddle.to_tensor([[1, 1, 1, 1], [1, 0, 0, 1]], stop_gradient=False))

# 生成随机数据集
num_samples = 100  # 数据集大小
x_dataset = paddle.randn([num_samples, 2])  # 随机生成输入
y_dataset = paddle.sum(x_dataset, axis=1, keepdim=True)  # 生成标签（这里简单地使用输入的两列之和）

# 设置优化器和损失函数
optimizer = SGD(learning_rate=0.01, parameters=model.parameters())
criterion = nn.MSELoss()

# 训练模型
num_epochs = 10  # 训练轮数
for epoch in range(num_epochs):
    for i in range(num_samples):
        # 获取单个样本
        x = paddle.unsqueeze(x_dataset[i], axis=0)  # 增加一个批次维度
        y = paddle.unsqueeze(y_dataset[i], axis=0)

        # 前向传播
        outputs = model(x)

        # 计算损失
        loss = criterion(outputs, y)

        # 反向传播和参数更新
        loss.backward()        # 反向传播，计算当前梯度
        optimizer.step()       # 根据梯度更新参数
        model.clear_gradients() # 清空过往梯度

    print(f'Epoch {epoch+1}/{num_epochs}, Loss: {loss.numpy()}')

# 输出更新后的参数与原版本参数
print("Updated Parameters:")
print("Hidden Layer Weights:", model.hidden_layer.weight.numpy())
print("Output Layer Weights:", model.output_layer.weight.numpy())

Pytorch

import torch
import torch.nn as nn
import torch.optim as optim

# 定义模型
class SimpleNN(nn.Module):
    def __init__(self):
        super(SimpleNN, self).__init__()
        self.hidden_layer = nn.Linear(2, 4, bias=False)
        self.output_layer = nn.Linear(4, 2, bias=False)
        self.activation = nn.ReLU()

    def forward(self, x):
        x = self.hidden_layer(x)
        x = self.activation(x)
        x = self.output_layer(x)
        return x

# 实例化模型
model = SimpleNN()

# 设置参数（权重）
model.hidden_layer.weight.data = torch.tensor([[1, 2], [2, 3], [1, 1], [3, 1]], dtype=torch.float,requires_grad=True)
model.output_layer.weight.data = torch.tensor([[1, 1, 1, 1], [1, 0, 0, 1]],dtype=torch.float, requires_grad=True)

# 生成随机数据集
num_samples = 100  # 数据集大小
x_dataset = torch.randn(num_samples, 2)  # 随机生成输入
y_dataset = x_dataset.sum(dim=1, keepdim=True)  # 生成标签（这里简单地使用输入的两列之和）

# 设置优化器和损失函数
optimizer = optim.SGD(model.parameters(), lr=0.01)
criterion = nn.MSELoss()

# 训练模型
num_epochs = 10  # 训练轮数
for epoch in range(num_epochs):
    for i in range(num_samples):
        # 获取单个样本
        x = x_dataset[i].unsqueeze(0)  # 增加一个批次维度
        y = y_dataset[i].unsqueeze(0)

        # 前向传播
        outputs = model(x)

        # 计算损失
        loss = criterion(outputs, y)

        # 反向传播和参数更新
        optimizer.zero_grad()  # 清空过往梯度
        loss.backward()        # 反向传播，计算当前梯度
        optimizer.step()       # 根据梯度更新参数

    print(f'Epoch {epoch+1}/{num_epochs}, Loss: {loss.item()}')

# 输出更新后的参数与原版本参数
print("Updated Parameters:")
print("Hidden Layer Weights:", model.hidden_layer.weight.data)
print("Output Layer Weights:", model.output_layer.weight.data)