❗写在前面 ❗：
 
… … … … … … … … . … … …
1️⃣ 提供两种语言实现：本文提供两种语言实现，分别为Python和C++，分别依赖的核心库为Numpy和Eigen.
 
2️⃣ 提供关键步的公式推导：写出详尽的公式推导太花时间，所以只提供了关键步骤的公式推导。更详尽的推导，可移步其他博文或相关书籍.
 加粗样式
3️⃣ 重在逻辑实现：文中的代码主要以实现算法的逻辑为主，在细节优化上面，并没有做更多的考虑，如果发现有不完善的地方，欢迎指出.
 
 
🌞 欢迎关注专栏，相应的内容会持续更新，祝大家变得更强！！
… … … … … … … … . … … …
 

1、原理推导

 
“三个臭皮匠，顶过一个诸葛亮”。Adaboost(自适应提升算法)，就是这样的一个算法思想。Adaboost是一种通过改变训练样本权重来学习多个弱分类器并线性组合成强分类器的Boosting算法。

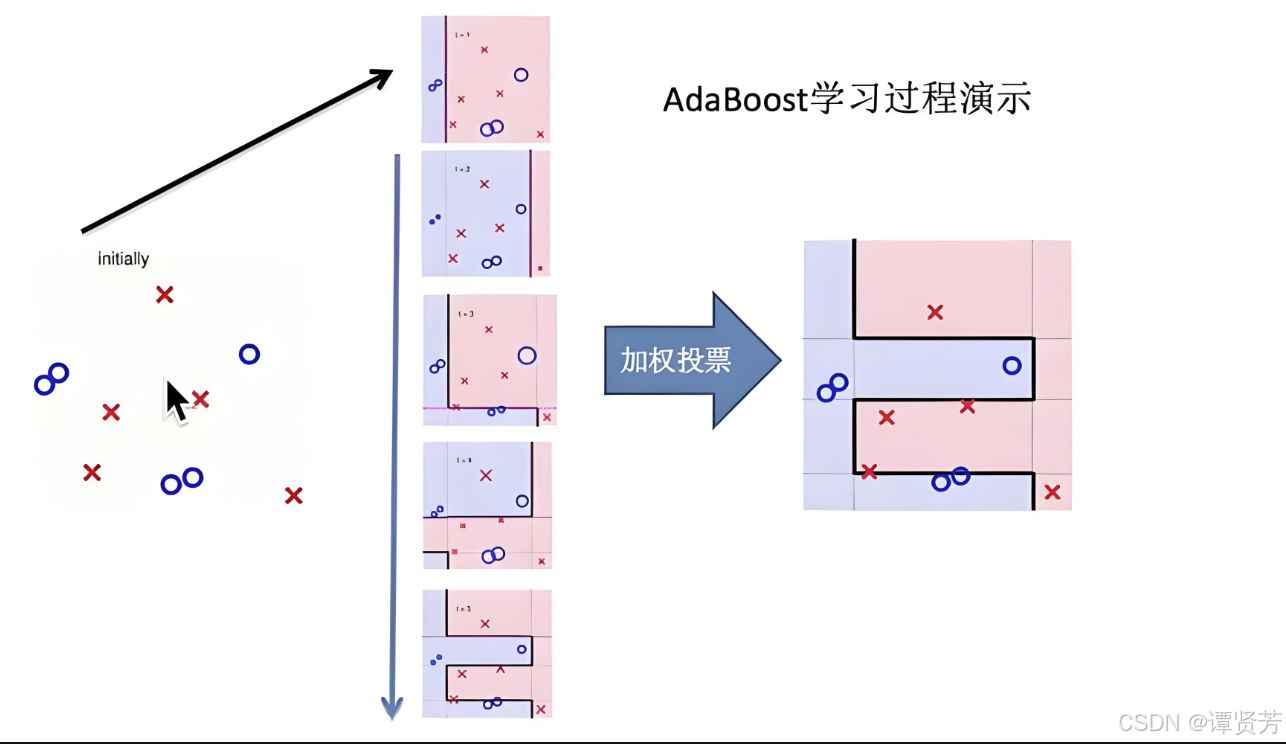
将弱分类器组合成一个强分类器方面：Adaboost是通过将多个若分类器进行线性组合，提高分类效果好的弱分类器，降低分类误差率高的分类器的权重实现的。

改变训练样本权重或者概率分布方面：Adaboost是通过提高前一轮被若分类分类错误的样本的权重，降低正确分类样本的权重来实现的。
 
 
 给定训练集 $D=\{(x_1,y_1),(x_2,y_2),...,(x_N,y_N)\}$，其中xi∈Rn,yi∈{−1，+1}x_i∈R^n,y_i∈\{-1，+1\}xi​∈Rn,yi​∈{−1，+1}，
 

① 初始化训练样本权重分布，即为每个训练样本分配一个初始权重：

 
    $D_1=(w_{11},...,w_{1i},...,w_{1N}),w_{1i}=\frac{1}{N},i=1,2,...,N$
 

② 对于$t=1,2,...,T$,分别执行：
 
  (a) 对包含权重分布$D_t$的训练集进行训练得到弱分类器$G_t(x)$。
 

  (b) 计算$G_t(x)$在当前加权训练集上的分类误差率：
 
      ${\epsilon }_t=P(G_t(x_i)\ne y_i)=\sum _{i=1}^N{w}_{ti}I(G_t(x_i)\ne y_i)$

  (c) 根据分类误差率计算当前弱分类器的权重系数${\alpha }_t$:
 
      ${\alpha }_t=\frac{1}{2}log\frac{1-{\epsilon }_t}{{\epsilon }_t}$
 
  (d) 调整训练集的权重分布：

      $D_{t+1}=(w_{t1},...,w_{ti},...,w_{tN})$

          $w_{t+1,i}=\frac{w_{ti}}{Z_t}$exp$(-{\alpha }_t{y}_i{G}_t(x_i))$

  其中$Z_t$为归一化因子，$Z_t=\sum _{i=1}^N{w}_{ti}$exp$(-{\alpha }_t{y}_i{G}_t(x_i))$
 

③ 最后构建$T$个弱分类器的线性组合：
 

      $f(x)=\sum _{t=1}^T{\alpha }_t{G}_t(x)$
 

  最终的强分类器可以写为：
 

      $G(x)=$ sign$(f(x))$
 

在弱分类器的权重系数计算的过程中，当若分类器的分类误差率${\epsilon }_t\le \frac{1}{2}$时，${\alpha }_t\ge 0$，且${\alpha }_t$随着${\epsilon }_t$的减小而变大，这就使得分类误差率较低的分类器有较大的权重系数。

其中训练样本权重分布可以写成：

           $\frac{w_{ti}}{Z_t}{e}^{-\alpha },G_t(x_i)=y_i$

      $w_{t+1,i}=$

           $\frac{w_{ti}}{Z_t}{e}^{\alpha },G_t(x_i)\ne y_i$

 
由此知道，当样本被弱分类器正确分类时，它的权重变小，当样本被弱分类器错误分类时，它的权重变大。相比之下，错误分类样本的权重增大了$e^{2{\alpha }_t}$倍，这就使得在下一轮训练中，算法会更加关注这些误分类样本。
 
 

2、算法实现

 

⚡C++实现

 

#include <iostream>
#include <vector>
#include <cmath>
#include <Eigen/Dense>
#include <unordered_set>

using namespace std;
using namespace Eigen;

// 定义决策树桩作为Adaboost弱分类器 
struct DecisionStump {
    int label;        // 分类器的预测标签
    int featureIdx;   // 特征的索引
    double threshold; // 划分阈值
    double alpha;     // Adaboost中的权重
};

class Adaboost {
private:
    vector<DecisionStump> estimators;  // 学习器向量
    int m_estimatorNum;                // 学习器的个数

    void sign(VectorXd& prediction) {
        for (int i = 0; i < prediction.size(); i++) {
            prediction(i) = prediction(i) < 0 ? -1 : 1;
        }
    }

public:
    Adaboost(int estimatorNum) : m_estimatorNum(estimatorNum) {}

    // 训练强学习器
    void fit(const MatrixXd& X, const VectorXd& y) {
        int trainNum = X.rows();
        int featureNum = X.cols();

        VectorXd w = VectorXd::Ones(trainNum) / trainNum;

        for (int n = 0; n < m_estimatorNum; ++n) {
            DecisionStump estimator;
            double min_error = std::numeric_limits<double>::infinity();

            // 遍历每个特征
            for (int fi = 0; fi < featureNum; fi++) {
                VectorXd fv = X.col(fi);  // 获取第fi列的特征向量
                std::unordered_set<double> fv_unique(fv.data(), fv.data() + fv.size());

                // 遍历每个特征的唯一值作为阈值
                for (const auto& threshold : fv_unique) {
                    int p = 1;  // 初始标签预测为正类

                    // 根据阈值进行预测
                    VectorXd pred(trainNum);
                    for (int j = 0; j < trainNum; j++) {
                        pred(j) = fv(j) < threshold ? 1 : -1;
                    }

                    // 计算误差率
                    double error = (pred.array() != y.array()).cast<double>().sum() / trainNum;
                    if (error > 0.5) {
                        p = -1;  // 若误差率大于0.5则反转标签预测
                        error = 1.0 - error;
                    }

                    // 更新最小误差率对应的决策树桩
                    if (error < min_error) {
                        estimator.featureIdx = fi;
                        estimator.label = p;
                        estimator.threshold = threshold;
                        min_error = error;
                    }
                }
            }

            // 计算当前学习器的权重alpha
            estimator.alpha = 0.5 * log((1 - min_error) / (min_error + 1e-9));
            estimators.push_back(estimator);

            // 更新样本权重
            VectorXd y_pred(trainNum);
            for (int j = 0; j < trainNum; j++) {
                y_pred(j) = X(j, estimator.featureIdx) < estimator.threshold ? 1 : -1;
            }
            w = w.array() * exp(-estimator.alpha * y.array() * y_pred.array());
            w /= w.sum();
        }
    }

    // 预测标签
    VectorXd predict(const MatrixXd& X) {
        int predNum = X.rows();
        VectorXd y_pred = VectorXd::Zero(predNum);

        for (const auto& estimator : estimators) {
            VectorXd prediction(predNum);
            for (int j = 0; j < predNum; j++) {
                prediction(j) = X(j, estimator.featureIdx) < estimator.threshold ? 1 : -1;
            }
            y_pred += prediction * estimator.alpha;
        }

        cout << y_pred.transpose() << endl;
        sign(y_pred);

        return y_pred;
    }
};

 

🌈Python实现

 

class DecisionStump:
    def __init__(self):
        self.label = None         # 分类器的预测标签
        self.featureIdx = None  # 特征的索引
        self.threshold = None   # 划分阈值
        self.alpha = None       # Adaboost中的权重

class NumpyAdaBoost:
    def __init__(self, n_estimator=5):
        self.n_estimator = n_estimator  # 弱分类器的数量
        self.estimators = []            # 存储每个弱分类器的列表

    def fit(self, X, y):
        self.estimators.clear()  # 清空之前的弱分类器列表
        
        m, n = X.shape
        w = np.full(m, 1 / m)  # 初始化样本权重，均匀分布
        
        for _ in range(self.n_estimator):
            estimator = DecisionStump()  # 创建一个决策树桩

            minError = np.inf  # 初始化最小误差为无穷大
            
            # 遍历每个特征
            for i in range(n):
                featureValues = np.expand_dims(X[:, i], axis=1)  # 获取第 i 列特征的所有取值
                uniqueFeatureValues = np.unique(featureValues)    # 获取唯一的特征取值

                # 遍历每个特征取值作为阈值
                for threshold in uniqueFeatureValues:
                    p = 1  # 初始化标签预测为正类
                    predict = np.ones(np.shape(y))  # 初始化预测标签为全部为正类

                    # 根据阈值进行预测
                    predict[X[:, i] < threshold] = -1

                    # 计算加权误差
                    error = np.sum(w[y != predict])

                    # 如果误差大于0.5，则反转预测标签
                    if error > 0.5:
                        error = 1 - error
                        p = -1
                    
                    # 更新最小误差对应的决策树桩参数
                    if error < minError:
                        estimator.label = p
                        estimator.threshold = threshold
                        estimator.featureIdx = i
                        minError = error
            
            # 计算当前弱分类器的权重alpha
            estimator.alpha = 0.5 * np.log((1.0 - minError) / (minError + 1e-10))

            # 根据当前弱分类器进行预测
            preds = np.ones(np.shape(y))

            negativeIdx = (estimator.label * X[:, estimator.featureIdx] < estimator.label * estimator.threshold)
            preds[negativeIdx] = -1

            # 更新样本权重
            w *= np.exp(-estimator.alpha * y * preds)
            w /= np.sum(w)

            # 将当前弱分类器添加到列表中
            self.estimators.append(estimator)

    def predict(self, X):
        m = X.shape[0]
        y_pred = np.zeros((m, 1))

        # 对每个弱分类器进行预测
        for estimator in self.estimators:
            predictions = np.ones(np.shape(y_pred))

            # 根据决策树桩的参数进行预测
            negativeIdx = (estimator.label * X[:, estimator.featureIdx] < estimator.label * estimator.threshold)
            predictions[negativeIdx] = -1

            # 根据弱分类器的权重alpha进行加权
            y_pred += estimator.alpha * predictions
        
        # 使用符号函数得到最终的预测标签
        y_pred = np.sign(y_pred).flatten()

        return y_pred

 

3、总结

 
AdaBoost 的优点：

准确性高：通过在每一轮迭代后调整对训练数据实例的关注度（特别是那些之前被错误预测的样本）和更新弱学习器的权重，最后将不同的弱学习器以不同的权重组合在一起，以输出最终的预测结果。AdaBoost 通常能够达到较好的预测性能。

易于代码实现：相对于其他复杂算法，AdaBoost 算法容易实现。并且默认参数就能取得不错的效果。

自动处理特征选择：AdaBoost 可以自动选择有效特征，并且忽略不相关或噪声特征。

灵活性：可与各种类型数据和不同类型问题配合使用。

不太容易过拟合：在许多实践中，尽管增加了复杂度，但 AdaBoost 往往不容易过拟合。

AdaBoost 的不足：

噪声敏感性：对噪声和异常值敏感。由于算法会给错误预测样本更高权重，因此噪声和异常值可能会导致模型表现不佳。

计算量较大：尽管单个模型可能简单，但需要顺序训练多个模型可能导致计算量增大。由于 AdaBoost 是一种迭代算法，需要顺序训练大量弱学习器，因此在处理大规模数据集或高维特征时，其计算量可能会变得相当大。

数据不平衡问题：在面对极端不平衡数据时表现可能不佳。

总体而言，AdaBoost 是一种简单而高效的算法，适合作为解决分类问题的起点。然而，在应用时，需要注意其对噪声和异常值的敏感性。