间隔与支持向量

给定训练样本集D={(x1,y1),(x2,y2)⋯ ,(xn,yn)},yi∈{−1,+1}D=\{(x_1,y_1),(x_2,y_2)\cdots, (x_n,y_n)\},y_i\in \{-1, +1\}D={(x1​,y1​),(x2​,y2​)⋯,(xn​,yn​)},yi​∈{−1,+1}，分类学习的最基本的思想就是基于样本空间中找个一个划分超平面，将不同类别的样本分开，但是超平面可能有很多种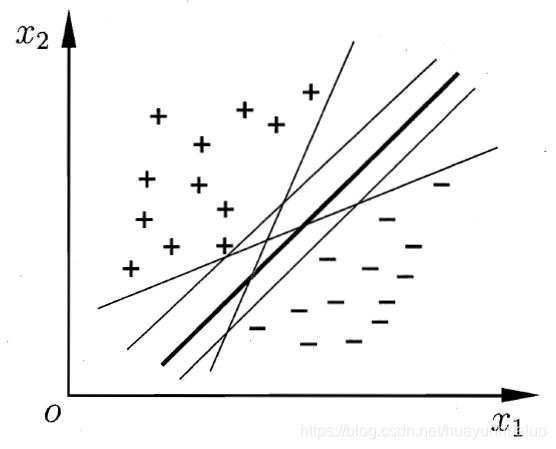

直观上应该找最中间的划分超平面，因为该超平面对训练样本局部的扰动的容忍最好的。由于训练集的局限性或噪声的因素，训练集外的样本可能更接近两个类的分隔界，这个划分超平面所产生的分类结果是最鲁棒的，对未见的示例泛化能力最强。

超平面的线性方程描述：
$${\omega \text{ω}\omega }^{T}x+b=0$$
其中$\omega \text{ω}\omega =({\omega }_1;{\omega }_2;\cdots ;{\omega }_d)$为法向量，决定超平面的方向，$b$为位移项，决定了超平面与原点之间的距离。

样本空间中任意点$x$到超平面$(\omega ,b)$的距离可写成：
$$r=\frac{|{\omega }^{\mathrm{T}}\mathrm{x}+\mathrm{b}|}{||\omega ||}$$
假设超平面$(\omega ,b)$能将训练样本正确分类，即对于$(x_i,y_i)\in D$，若$y_i=+1$，则有$w^T{x}_i\text{wTxi}{w}^T{x}_i+b>0$，若$y_i=-1$，则有${\omega }^T{x}_i\text{ωTxi}{\omega }^T{x}_i+b<0$
$$\{\begin{array}{ll}{\omega }^T{x}_i\text{ωTxi}{\omega }^T{x}_i+b\ge +1& y_i=+1\\ {\omega }^T{x}_i\text{ωTxi}{\omega }^T{x}_i+b\le -1& y_i=-1\end{array}$$
推导：

假设这个超平面是${\omega }^{{}^{\prime }T}x+b^{{}^{\prime }}=0$，则对于$(x_i,y_i)\in D$，有：
$$\{\begin{array}{ll}{\omega }^{{}^{\prime }T}{x}_i+b^{{}^{\prime }}>0& y_i=+1\\ {\omega }^{{}^{\prime }T}{x}_i+b^{{}^{\prime }}<0& y_i=-1\end{array}$$
根据几何间隔，将以上关系修正为
$$\{\begin{array}{ll}{\omega }^{{}^{\prime }T}{x}_i+b^{{}^{\prime }}\ge +\zeta & y_i=+1\\ {\omega }^{{}^{\prime }T}{x}_i+b^{{}^{\prime }}\le -\zeta & y_i=-1\end{array}$$
其中$\zeta$为某个大于零的常数，两边同时除以$\zeta$，再次修改以上关系
$$\{\begin{array}{ll}\frac{1}{\zeta }{\omega }^{{}^{\prime }T}{x}_i+\frac{1}{\zeta }{b}^{{}^{\prime }}\ge +1& y_i=+1\\ \frac{1}{\zeta }{\omega }^{{}^{\prime }T}{x}_i+\frac{1}{\zeta }{b}^{{}^{\prime }}\le -1& y_i=-1\end{array}$$
令$\omega =\frac{1}{\zeta }{\omega }^{{}^{\prime }},b=\frac{b^{{}^{\prime }}}{\zeta }$，就可以得到公式。

距离超平面最近的这几个训练样本使等号成立，它们称之为支持向量（support vector）,两个异类支持向量到超平面的距离之和为
$$\gamma =\frac{2}{||\omega \text{ω}\omega ||}$$

找到具有最大间隔的划分超平面，就要找到满足条件参数的$\omega$和$b$，使$\gamma$最大
$$\begin{gathered} \underset{w,b}{\max }\frac{2}{||w||} \\ s.t.y_i(w^T{x}_i\text{wTxi}{w}^T{x}_i+b)\ge 1,i=1,2,\cdots ,m \end{gathered}$$
为了最大化间隔，仅需要最大化$||w|{|}^{-1}$，这等价于最下化$||w|{|}^2$
$$\begin{gathered} \underset{w,b}{\min }\frac{1}{2}||w|{|}^2 \\ s.t.y_i(w^T{x}_i\text{wTxi}{w}^T{x}_i+b)\ge 1,i=1,2,\cdots ,m \end{gathered}$$

对偶问题

对于最大间隔划分超平面对应的模型
$$f(x\text{x}x)=w^{T}x\text{wTx}{w}^{T}x+b$$
这是一个凸二次规划（convex quadratic programming）问题

使用拉格朗日乘子法可以得到其对偶问题，对于每个约束添加拉格朗日乘子${\alpha }_i\ge 0$，则该问题是拉格朗日函数为：
$$L(\omega \text{ω}\omega ,b,\alpha )=\frac{1}{2}||w\text{w}w|{|}^2+\sum _{i=1}^m{\alpha }_i(1-y_i(w^T{x}_i+b))$$
其中$\alpha \text{α}\alpha =({\alpha }_1,{\alpha }_2,\cdots ,{\alpha }_m)$。令$L(\omega \text{ω}\omega ,b,\alpha )$对$\omega \text{ω}\omega$和$b$的偏导为零可得
$$\begin{gathered} \omega \text{ω}\omega =\sum _{i=1}^m{\alpha }_i{y}_i{x}_i\text{xi}{x}_i \\ 0=\sum _{i=1}^m{\alpha }_i{y}_i \end{gathered}$$
推导：
$$\begin{array}{rl}L(w\text{w}w,b,\alpha )& =\frac{1}{2}||w|{|}^2+\sum _{i=1}^m{\alpha }_i(1-y_i(w^t{x}_i+b))\\ & =\frac{1}{2}||w|{|}^2+\sum _{i=1}^m({\alpha }_i-{\alpha }_i{y}_i{w}^T{x}_i-{\alpha }_i{y}_{i}b)\\ & =\frac{1}{2}{\omega }^T\omega +\sum _{i=1}^m{\alpha }_i-\sum _{i=1}^m{\alpha }_i{y}_i{w}^T{x}_i-\sum _{i=1}^m{\alpha }_i{y}_{i}b\end{array}$$
对$\omega$和$b$分别求偏函数并令等于0
$$\begin{gathered} \frac{\partial L}{\partial w\text{w}w}=\omega +0-\sum _{i=1}^m{a}_i{y}_i{x}_i-0=0\Rightarrow w\text{w}w=\sum _{i=1}^m{\alpha }_i{y}_i{x}_i \\ \frac{\partial L}{\partial b}=0+0-0-\sum _{i=1}^m{\alpha }_i{y}_i=0\Rightarrow \sum _{i=1}^m{\alpha }_i{y}_i=0 \end{gathered}$$
可以得到对偶问题
$$\begin{gathered} \underset{\alpha }{\max }\sum _{i=1}^m{\alpha }_i-\frac{1}{2}\sum _{i=1}^m\sum _{j=1}^m{\alpha }_i{\alpha }_j{y}_i{y}_j{x}_i^T{x}_j \\ s.t.\sum _{i=1}^m{\alpha }_i{y}_i=0 \\ {\alpha }_i\ge 0,i=1,2,\cdots ,m \end{gathered}$$
推导：
$$\begin{array}{rl}\underset{w,b}{\min }L(w,b,\alpha )& =\frac{1}{2}{w}^w+\sum _{i=1}^m{\alpha }_i-\sum _{i=1}^m{\alpha }_i{y}_i{w}^T{x}_i-\sum _{i=1}^m{\alpha }_i{y}_{i}b\\ & =\frac{1}{2}{\omega }^T\sum _{i=1}^m{\alpha }_i{y}_i{x}_i-w^T\sum _{i=1}^m{\alpha }_i{y}_i{x}_i+\sum _{i=1}^m{\alpha }_i-b\sum _{i=1}^m{\alpha }_i{y}_i\\ & =-\frac{1}{2}{w}^T\sum _{i=1}^m{\alpha }_i{y}_i{x}_i+\sum _{i=1}^m{\alpha }_i-b\sum _{i=1}^m{\alpha }_i{y}_i\end{array}$$
由于${\sum }_{i=1}^m{\alpha }_i{y}_i=0$，所以
$$\begin{array}{rl}\underset{w,b}{\min }L(w,b,\alpha )& =-\frac{1}{2}{w}^T\sum _{i=1}^m{\alpha }_i{y}_i{x}_i+\sum _{i=1}^m{\alpha }_i\\ & =-\frac{1}{2}(\sum _{i=1}^m{\alpha }_i{y}_i{x}_i{)}^T(\sum _{i=1}^m{\alpha }_i{y}_i{x}_i)+\sum _{i=1}^m{\alpha }_i\\ & =-\frac{1}{2}(\sum _{i=1}^m{\alpha }_i{y}_i{x}_i^T)(\sum _{i=1}^m{\alpha }_i{y}_i{x}_i)+\sum _{i=1}^m{\alpha }_i\\ & =\sum _{i=1}^m{\alpha }_i-\frac{1}{2}\sum _{i=1}^m\sum _{j=1}^m{\alpha }_i{\alpha }_j{y}_i{y}_j{x}_i^T{x}_j\end{array}$$
所以
$$\underset{\alpha }{\max }\underset{w,b}{\min }=\underset{\alpha }{\max }\sum _{i=1}^m{\alpha }_i-\frac{1}{2}\sum _{i=1}^m\sum _{j=1}^m{\alpha }_i{\alpha }_j{y}_i{y}_j{x}_i^T{x}_j$$
解出$\alpha$后，求出$w,b$即可得到模型

上述过程需要满足KKT(Karush-Kuhn-Tucker)条件，即要求
$$\{\begin{array}{l}{\alpha }_i\ge 0\\ y_{i}f(x_i)-1\ge 0\\ {\alpha }_i(y_{i}f(x_i)-1)=0\end{array}$$
对于任意训练样本$(x_i,y_i)$，总有${\alpha }_i=0$或$y_{i}f(x_i)=1$，若${\alpha }_i=0$，则这样的样本不会出现在求和中，对$f(x)$有任何影响。若${\alpha }_i>0$，则必有$y_{i}f(x_i)=1$，则对应的样本点在于最大分隔边界上，是一个支持向量。

如何求解呢，这是一个二次规划问题，可以使用通用的二次规划算法来求解，其中高效的算法有很多，其中SMO（Sequential Minimal Optimization）是其中一个著名的代表。

SMO的基本思想是先管你的固定${\alpha }_i$之外的所有参数，然后求${\alpha }_i$上的极限。。由于存在约束${\sum }_{i=1}^m{\alpha }_i{y}_i=0$，若固定${\alpha }_i$之外的其他变量，则${\alpha }_i$可由其他变量导出。于是，SMO每次选择两个变量${\alpha }_i$和${\alpha }_j$，并固定其他参数。

• 选择一对需要更新的变量${\alpha }_i$和${\alpha }_j$
• 固定${\alpha }_i$和${\alpha }_j$以外的参数，求解更新后的${\alpha }_i$和$\alpha_j $

注意到只需选取的${\alpha }_i$和${\alpha }_j$中有一个不满足KKT条件，目标函数就会在迭代后减少，于是，SMO先选取违背KKT条件的最大的变量，第二个变量应选择一个使目标函数值减少最快的变量，但是比较各变量所对应的目标函数值减少幅度复杂度过高，因此SMO采用了一个启发式：使选择的两变量所对应样本之间的间隔最大，一种直观解释就是，这样的两个变量有很大的差别，与对两个相似的变量进行更新相比，对他们更新会给目标函数值更大的变化。

SMO算法值所以高效，由于在固定其他参数后，优化两个参数的过程能够非常有效。具体来说，仅考虑${\alpha }_i$和${\alpha }_j$时，约束可以重新写成：
$${\alpha }_i{y}_i+a_j{y}_j=c,{\alpha }_i\ge 0,{\alpha }_j\ge 0$$
其中
$$c=-\sum _{k\ne i,j}{a}_k{y}_k$$
消去${\alpha }_j$，则得到一个关于${\alpha }_i$的单变量二次规划问题，仅有约束${\alpha }_i\ge 0$ 。这样的二次规划问题具有闭式解，于是不必调用数值优化算法即可高效的计算出更新后的${\alpha }_i$和${\alpha }_j$

对于$y_{S}f(x_S\text{xS}{x}_S=1)$
$$y_s(\sum _{i\in S}{\alpha }_i{y}_i{x}_i^T{x}_s\text{xiTxs}{x}_i^T{x}_s+b)=1$$
其中S={i∣αi>0,i=1,2,3,⋅,m}S = \{i|\alpha_i>0,i=1,2,3,\cdot,m\}S={i∣αi​>0,i=1,2,3,⋅,m}所支持向量的下标集。
$$b=\frac{1}{|S|}\sum _{s\in S}(y_s-\sum {\alpha }_i{y}_i{x}_i^T{x}_s\text{xiTxs}{x}_i^T{x}_s)$$

核函数

在实际的任务中，原始样本空间内也许不存在一个能正确划分两类样本的超平面，对于这样的问题，可将样本从原始空间映射到一个更高维的特征空间，使得样本在这个特征空间内线性可分。

令$\varphi (x\text{x}x)$表示将$x\text{x}x$映射后的特征向量，于是，在特征空间中划分超平面所对应的模型可表示为
$$f(x\text{x}x)={w\text{w}w}^T\varphi (x\text{x}x)+b$$
其中$w\text{w}w$和$b$是参数模型
$$\begin{gathered} \underset{w\text{w}w,b}{\min }\frac{1}{2}||w\text{w}w|{|}^2 \\ s.t.y_i({w\text{w}w}^T\varphi (x_i\text{xi}{x}_i)+b)\ge 1,i=1,2,\cdots ,m \end{gathered}$$
对偶问题是：
$$\begin{gathered} \underset{\alpha }{\max }\sum _{i=1}^m{\alpha }_i-\frac{1}{2}\sum _{i=1}^m\sum _{j=1}^m{\alpha }_i{\alpha }_j{y}_i{y}_j\varphi (x_i\text{xi}{x}_i{)}^T\varphi (x_j\text{xj}{x}_j) \\ s.t.\sum _{i=1}^m{\alpha }_i{y}_j=0,{\alpha }_i\ge 0,i=1,2,3\cdots ,m \end{gathered}$$
设计到计算$\varphi (x_i\text{xi}{x}_i{)}^T\varphi (x_j\text{xj}{x}_j)$,由于映射后的特征空间维数可能很高，甚至可能是无穷维的，因此直接计算$\varphi (x_i\text{xi}{x}_i{)}^T\varphi (x_j\text{xj}{x}_j)$通常是困难的。可以设想这样的一个函数
$$\kappa (x_i,x_j\text{xi,xj}{x}_i,x_j)=⟨\varphi (x_i\text{xi}{x}_i),\varphi (x_j\text{xj}{x}_j)⟩=\varphi (x_i\text{xi}{x}_i{)}^T\varphi (x_j\text{xj}{x}_j)$$
于是$x_i$与$x_j$在特征空间的内积等于他们在原始样本空间中通过函数$\kappa$来计算的结果。
$$\begin{gathered} \underset{\alpha }{\max }\sum _{i=1}^m{\alpha }_i-\frac{1}{2}\sum _{i=1}^m\sum _{j=1}^m{\alpha }_i{\alpha }_j{y}_i{y}_j\kappa (x_i,x_j\text{xi,xj}{x}_i,x_j) \\ s.t.\sum _{i=1}^m{\alpha }_i{y}_i=0,{\alpha }_i\ge 0,i=1,2,\cdots ,m \end{gathered}$$
求解后可得到
$$\begin{array}{rl}f(x)& ={w\text{w}w}^T\varphi (x\text{x}x)+b\\ & =\sum _{i=1}^m{\alpha }_i{y}_i\varphi (x_i\text{xi}{x}_i{)}^T\varphi (x_i\text{xi}{x}_i)+b\\ & =\sum _{i=1}^m{\alpha }_i{y}_i\kappa (x_i,x_j\text{xi,xj}{x}_i,x_j)+b\end{array}$$
这里的$\kappa$就是核函数，显示出来的模型最优解可通过训练样本的核函数展开，称为支持向量展式

核函数

令$\mathcal{X}$为输入空间，$\kappa (\cdot ,\cdot )$是定义在$\mathcal{X}\times \mathcal{X}$上的对称函数，则$\kappa$是核函数当且仅当对于任意数据D={x1,x2,,⋯ ,xm}D=\{\pmb{x_1,x_2,,\cdots,x_m}\}D={x1​,x2​,,⋯,xm​​x1​,x2​,,⋯,xm​​​x1​,x2​,,⋯,xm​}。核矩阵$K\text{K}K$总是半正定的
$$K\text{K}K=\left[\begin{array}{ccccc}\kappa (x_1,x_1\text{x1,x1}{x}_1,x_1)& \cdots & \kappa (x_1,x_j\text{x1,xj}{x}_1,x_j)& \cdots & \kappa (x_1,x_m\text{x1,xm}{x}_1,x_m)\\ ⋮& \ddots & ⋮& \ddots & ⋮\\ \kappa (x_i,x_1\text{xi,x1}{x}_i,x_1)& \cdots & \kappa (x_i,x_j\text{xi,xj}{x}_i,x_j)& \cdots & \kappa (x_i,x_m\text{xi,xm}{x}_i,x_m)\\ ⋮& \ddots & ⋮& \ddots & ⋮\\ \kappa (x_m,x_1\text{xm,x1}{x}_m,x_1)& \cdots & \kappa (x_m,x_j\text{xm,xj}{x}_m,x_j)& \cdots & \kappa (x_m,x_m\text{xm,xm}{x}_m,x_m)\end{array}\right]$$
表明只要一个对称函数所对应的的核矩阵半正定，就能作为核函数使用。任何一个核函数都隐式地定义一个称为再生核希尔伯特空间(Reproducing Kernel Hilbert Sapce,RKHS)的特征空间。

常用的核函数

还可以通过函数组合通过

• 若${\kappa }_1$和${\kappa }_2$为核函数，则对于任意整数${\gamma }_1,{\gamma }_2$其线性组合为
  $${\gamma }_1{\kappa }_1+{\gamma }_2{\kappa }_2$$
  也是核函数

• 若${\kappa }_1$和${\kappa }_2$是核函数，则核函数的直积
  $${\kappa }_1\otimes {\kappa }_2(x,z)={\kappa }_1(x,z){\kappa }_2(x,z)$$
  也是核函数

• 若${\kappa }_1$为核函数，则对于任意函数$g(x)$
  $$\kappa (x,z)=g(x){\kappa }_1(x,z)g(z)$$