一文彻底掌握人工智能中的无信息搜索（广度优先、深度优先、一致代价、迭代加深的深度优先）+有信息搜索（贪婪最佳优先、A*）
罗马尼亚问题+CPP代码实现+详细讲解+分析

下文中使用的代码：
pan.baidu.com/s/1uocOSj9ApTY6ITZJPpNg6g
提取码：1x2f

一、 实验目的

• 了解4种无信息搜索策略和2种有信息搜索策略的算法思想；
• 能够运用计算机语言实现搜索算法；
• 应用搜索算法解决实际问题(如罗马尼亚问题)；
• 学会对算法性能的分析和比较

二、 实验的硬件、软件平台

硬件：计算机
软件：操作系统：WINDOWS
应用软件：DEV C++

三、 实验内容及步骤

使用搜索算法实现罗马尼亚问题的求解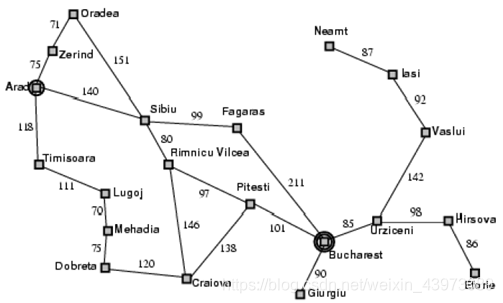

【求解罗马尼亚问题所需条件】

1、 城市信息存储

用CITY结构体保存城市信息，包括编号、名字、直线距离h、相邻城市的信息（vector next[0]存储相邻城市编号、next[1]存储到达该城市的路径耗费）
2、 树结点定义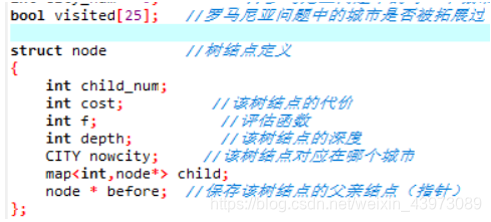

树结点包括该结点到达的城市、到达该城市的路径消耗cost、结点的深度、子结点信息（map child）、父节点信息（before用于查询树路径）、评估值f（用于一致代价、A*、贪婪最佳搜索的优先队列排序）
3、 优先队列排序参数

排序方式为结点按照评估值f从小到大排序，f相同则按照cost从小到大排。
4、 搜索路径

从终点开始根据结点中的before（父节点指针），追踪路径直到初始结点，递归打印出整条正向路径。
5、 城市信息读取

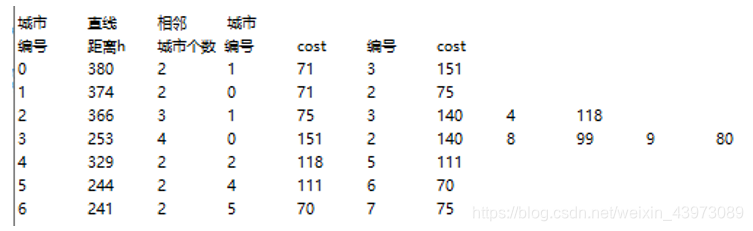
（仅截取部分）
将城市信息存储在map.txt文件中，第一个整数为城市数量n，接下来n行表示城市编号与名称，再接下来n行的前三列表示城市的编号、直线距离h、相邻城市数x，后面的2x列表示相邻城市的标号、路径耗费。

【无信息搜索策略】

1、 广度优先搜索

1） 算法原理
宽度优先搜索是简单搜索策略，先扩展根结点，接着扩展根结点的所有后继，然后再按照扩展顺序扩展它们的后继，依此类推。一般地，在下一层的任何结点扩展之前，搜索树上本层深度的所有结点都应该已经扩展过。
如果最浅的目标结点处于一个有限深度 d，那么宽度优先搜索是完备的，宽度优先搜索在扩展完比它浅的所有结点之后最终一定能找到该目标结点。但是，最浅的目标结点不一定是最优的目标结点。
2） 代码实现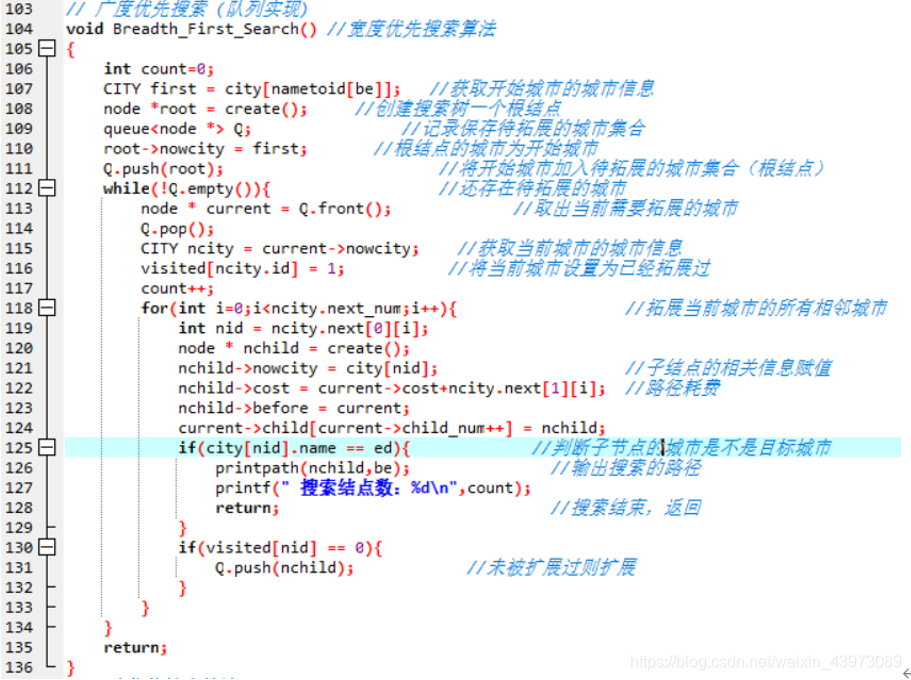

3） 实现说明
宽度优先搜索的具体实现采用的数据结构是队列，直接使用STL库的queue即可，算法步骤如下：
①根据开始城市Arid来创建搜索树的根结点，将根结点入队；
②判断此时队列是否为空，非空则：
③取出队首元素——待拓展的城市作为当前扩展城市，并标记当前城市已拓展；
④拓展当前城市的所有相邻城市。对于每一个相邻的城市，创建一个新的子结点，将当前相邻的城市城市信息、路径耗散赋给子结点，子结点的父结点为当前正在拓展的结点。
⑤此时判断子结点城市是不是目标城市，如果是，则输出搜索的路径，搜索结束。若不是目标城市，则继续下一步。（在扩展子结点时判断是否到达目标城市）
⑥对于每一个被扩展的子结点，判断对应的城市是否已经被拓展过，如果该相邻城市没被拓展过，则将该相邻城市加入队列中，回到②。
4） 运行结果

2、 深度优先算法

1） 算法原理
深度优先搜索总是扩展搜索树的当前边缘结点集中最深的结点。搜索很快推进到搜索树的最深层，那里的结点没有后继。当那些结点扩展完之后，就从边缘结点集中去掉，然后搜索算法回溯到下一个还有未扩展后继的深度稍浅的结点。
对于避免重复状态和冗余路径的图搜索，DFS在有限状态空间是完备的，因为它至多扩展所有结点，深度优先搜索不是最优的。
2） 代码实现

3） 实现说明
深度优先搜索依赖的数据结构是栈，可以满足DFS的LIFO队列需求，算法步骤如下：
①根据开始城市创建搜索树的根结点，姜根节点加入到栈中；
②判断此时栈是否为空，为空则结束，不为空则：
③取出栈顶元素，获取该结点的当前城市信息，并将当前城市标记已被拓展；
④判断当前城市是不是目标城市，如果是，则输出搜索的路径，搜索结束。若不是目标城市，则继续下一步。
⑤拓展当前城市的所有相邻城市。根据每一个相邻的城市创建一个新的子结点，根据相邻城市的信息与当前城市的信息对子结点进行赋值，子结点的父亲结点是当前正在拓展的结点，并且在当前结点的子节点表中加入该子结点。
⑥判断相邻城市是否已经被拓展过，如果该相邻城市没被拓展过，则将对应子结点栈中，回到②。
4） 运行结果

3、 一致代价搜索

1）算法原理
当每一步的行动代价都相等时宽度优先搜索是最优的，因为它总是先扩展深度最浅的未扩展结点。更进一步，我们可以找到一个对任何单步代价函数都是最优的算法。不再扩展深度最浅的结点，一致代价搜索扩展的是路径消耗最小的结点。这可以通过将边缘结点集组织成按单步代价值排序的优先队列来实现。
除了按路径代价对队列进行排序外，一致代价搜索和宽度优先搜索有两个显著不同。第一是目标检测应用于结点被选择扩展时，而不是在结点生成的时候进行。理由是第一个生成的目标结点可能在次优的路径上。第二个不同是如果边缘中的结点有更好的路径到达该结点那么会引入一个测试。
2）代码实现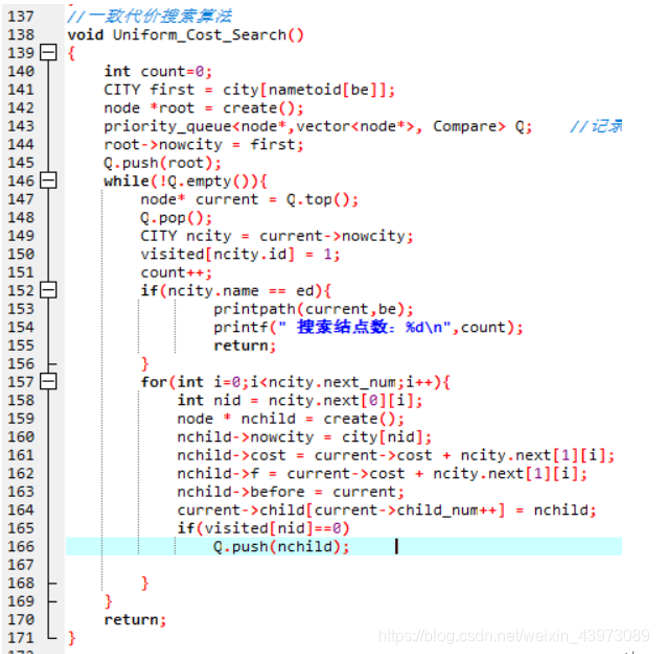

3）实现说明
实现 一致代价搜索算法 的数据结构是优先队列，直接使用STL库中的priority_queue，排序方法为结点中的评估值f从小到大排序，算法步骤如下：
①根据Arid的信息创建搜索树的根结点，将根节点加入优先队列中。
②判断此时优先队列是否为空，不为空则：
③取出 当前优先队列中队首 元素，获取当前需要拓展的城市城市信息，并将当前城市标记已被拓展。
④ 此时判断当前城市是不是目标城市，如果是，则输出搜索的路径，搜索结束。若不是，则继续下一步。
⑤拓展当前城市的所有相邻城市。对于每一个相邻的城市创建一个新的子结点，根据当前城市的信息和路径耗散给子结点赋值，尤其这里需要给子结点的评估值f赋值为路径耗散用来作为优先队列排序标准，子结点的父亲结点是当前正在拓展的结点，并且在当前结点的子结点队列中加入该子结点。

****⑥判断子结点中的城市是否被扩展过，若没有则将子结点都直接加入优先队列中，回到②。

（按书上源码应该是判断子结点的城市是否已经被加入优先队列，若是则需要判断它的f是否小于队列中对应结点的f，小于则更新队列中的元素。但这里用了优先队列实现，那么直接加入队列后若f小于已存在的城市结点的f，加入的结点会排在它前面，因此不需要进行更新即可）

4）运行结果

4、 迭代加深的深度优先搜索

1）算法思想
深度受限搜索：对深度优先搜索设置限界l来避免无限状态空间中的无穷路径问题，深度超过l的结点被当作没有后继结点对待。
迭代加深的深度优先搜索：
迭代加深的深度优先搜索是基于深度受限搜索的一种策略，它经常和深度优先搜索结合使用来确定最好的深度界限。做法是不断地增大深度限制——首先为 0，接着为 1，然后是 2，以此类推直到找到目标。当深度界限达到 d，即最浅的目标结点所在深度时，就能找到目标结点。
迭代加深的深度优先搜索算法结合了深度优先搜索和宽度优先搜索的优点，它的空间需求是合适的：O(bd)。和宽度优先搜索一样，当分支因子有限时是该搜索算法是完备的，当路径代价是结点深度的非递减函数时该算法是最优的。

2）代码实现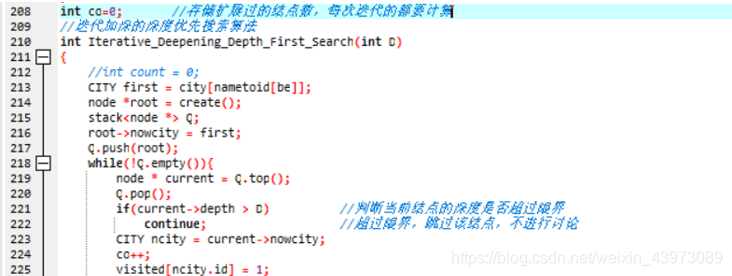


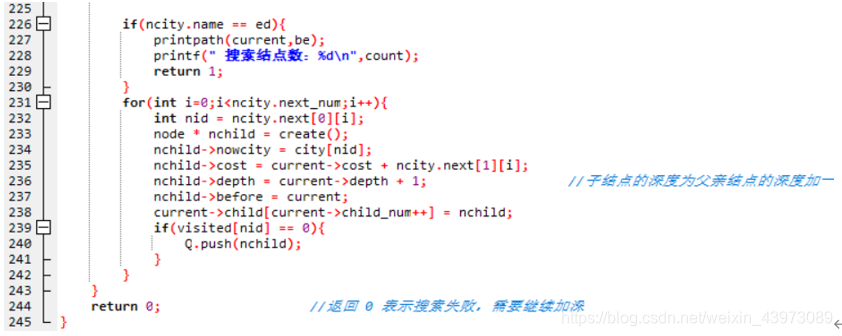
在main函数中迭代调用迭代加深的深度优先函数，每次调用都对限界值参数加1，直到找到目标城市。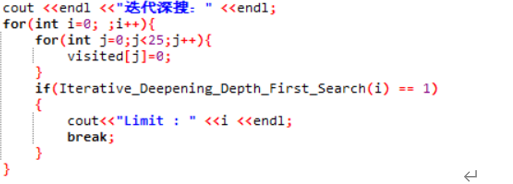

3）实现说明
实现 迭代加深的深度优先搜索算法 的数据结构与深度优先相同都是栈，算法步骤如下：
①根据Arid信息创建搜索树的根结点，将根结点的深度初始化为 0，将根结点加入栈中。
②判断此时栈是否为空，若为空，返回搜索失败，需要继续迭代加深界限值，否则：
③ 取出 栈中栈顶元素，判断当前结点的深度是否超过限界，如果深度超过限界，跳过该结点。如果深度没有超过限界，则获取当前结点的城市信息，并标记当前城市为已被拓展。
④ 此时判断当前城市是不是目标城市，如果是，则输出搜索的路径，返回搜索成功，搜索结束。若不是目标城市，则继续下一步。
⑤ 拓展当前城市的所有相邻城市。对于每一个相邻的城市，根据相邻城市的信息创建一个新的子结点，将当前相邻的城市城市信息赋给子结点，同时子结点的深度为父亲结点的深度加一。子结点的父亲结点是当前正在拓展的结点，并且在当前结点的孩子列表中加入该子结点。
⑥判断该相邻城市是否已经被拓展过，如果该相邻城市没被拓展过，则将该结点栈中。
4）运行结果

【有信息搜索】

5、 贪婪最佳优先搜索

1）算法思想
最佳优先搜索：结点基于评价函数值被选择扩展。评价函数被看作是代价评估，因此评估值最低的结点被选择首先进行扩展。最佳优先图搜索的实现与一致代价搜索类似，不过最佳优先是根据评价函数值f对优先级队列进行排队。
贪婪最佳优先搜索试图扩展离目标最近的结点，理由是这样可能可以很快找到解。因此，它只用启发式信息。对应到罗马尼亚问题中，使用直线距离启发式：

2）代码实现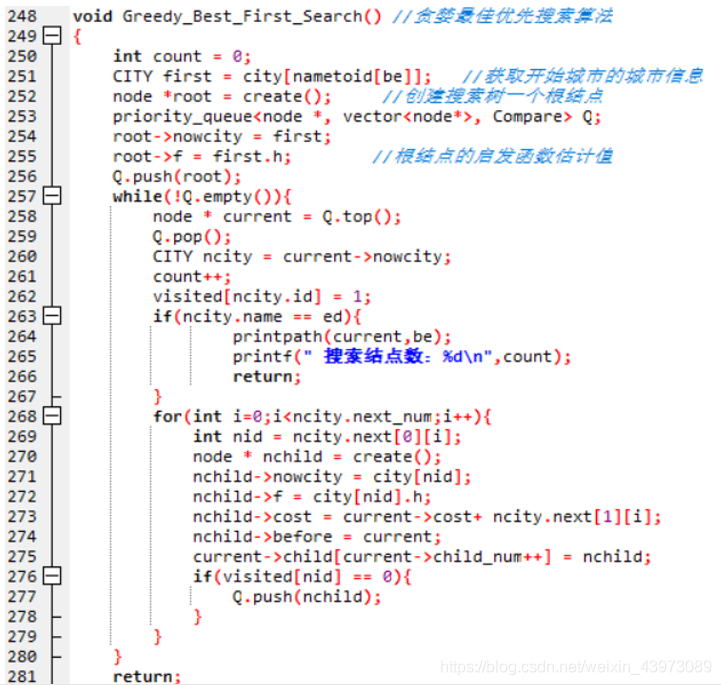

3）实现说明
实现 贪婪最佳优先搜索 的数据结构与A*、一致代价搜索相同都是优先队列，算法步骤如下：
①根据Arid的信息创建搜索树的根结点，将根节点加入优先队列中。
②判断此时优先队列是否为空，不为空则：
③取出 当前优先队列中队首 元素，获取当前拓展的城市信息，并将当前城市标记已被拓展。
④ 此时判断当前城市是不是目标城市，如果是，则输出搜索的路径，搜索结束。若不是，则继续下一步。
⑤拓展当前城市的所有相邻城市。对于每一个相邻的城市创建一个新的子结点，根据当前城市的信息和路径耗散给子结点赋值，尤其这里需要给子结点的评估值f赋值为城市的直线距离h用来作为优先队列排序标准，子结点的父亲结点是当前正在拓展的结点，并且在当前结点的子结点队列中加入该子结点。
⑥判断子节点的城市是否已被扩展，未扩展则将子结点都加入优先队列中，回到②，这里和下面的A*与一致代价搜索中部分提到理由相同的都不需要进行优先队列中是否已经存在该城市的判断。
4）运行结果

6、 A*搜索

1）算法思想
A* 搜索对结点的评估结合了到达此结点已经花费的代价，和从该结点到目标结点所花代价。由于结合了从开始结点到结点 n 的路径代价和从结点 n 到目标结点的最小代价路径的评估值，因此评估函数值等于经过结点 n 的最小代价解的估计代价。
这样，如果我们想要找到最小代价的解，首先扩展评估函数值最小的结点是合理的。可以发现这个策略不仅仅合理：假设启发式函数满足特定的条件，A* 搜索既是完备的也是最优的。
其中，A* 搜索算法的最优性取决于：如果启发式函数是可采纳的，那么 A* 的树搜索版本是最优的，如果启发式函数是一致的，那么图搜索的 A* 算法是最优的。
2）代码实现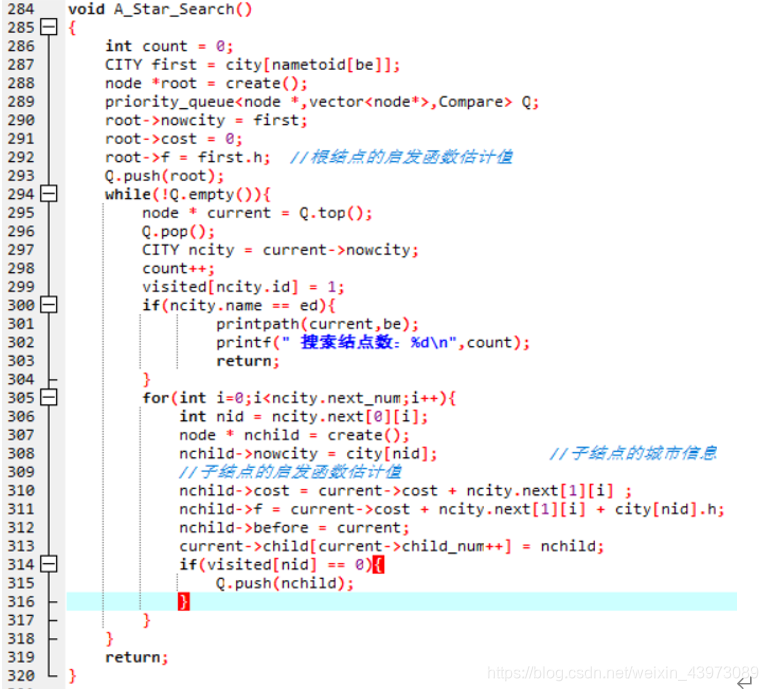

3）实现说明
A算法与一致代价搜索和贪婪最佳搜索在思想上大致相同，因此这里不再重复，它们最大的**区别在于结点评估值f的计算，A的评估值为根结点到当前结点的路径耗散cost加上当前节点的直线距离h；**
4）运行结果

四、 实验结果分析

1、 各个算法的复杂度
1） 宽度优先搜索
①是完备的（只要有解，肯定能搜到。当然，前提是最浅的目标节点处于一个有限深度d，分支因子b也是有限的）BFS找到的永远是最浅的目标节点；
②不一定最优，只有当路径代价是基于节点深度的非递减函数时，BFS是最优的（最常见情况是所有行动要花费相同的代价）。
③假设每个状态都有b个后继状态，解的深度为d，那么时间复杂度就是O(bd)O(bd)，空间复杂度也是O(bd)。

2） 一致代价搜索
①是最优的，如果每一步的代价都大于等于某个小的正常数，那么就是完备的。
②时间空间复杂度：O(b1+[C∗/e]),其中C∗是最优解的代价，每个行动的代价至少为e，所以最坏情况下，这个复杂度要比BFS的复杂度大的多，当所有单步耗散都相等时，复杂度变为bd+1；

3） 深度优先搜索
①DFS的搜索效率严重依赖于使用的是图搜索还是树搜索。
如果是图搜索（避免了重复状态和冗余路径），那么DFS在有限状态空间就是完备的。
如果是树搜索，则不完备，因为会出现死循环（DFS算法本身是没有explored set的）。
②不是最优的。
③复杂度：时间复杂度受限于状态空间的规模，为：O(bm)，m是任一节点的最大深度。这比d（最浅解的深度）要大的多，但是空间复杂度为O(bm)。

4） 迭代加深的深度优先
①在分支因子有限时完备，在路径耗散为节点深度的非递减函数时最优（和BFS一样）
②空间复杂度：O(bd) （和DFS一样），时间复杂度：O(bm)，m是任一节点的最大深度。

5） 贪婪最佳优先
①在有限状态空间是完备的，不是最优的
②时间复杂度为O(bm)，m是任一节点的最大深度。

6） A*
①h为可采纳的，因此A是完备且最优的
②时间复杂是为O（dx），x=h-h，h*为从根节点到目标结点的实际代价。

2、 根据扩展结点数目来进行直方图的绘制：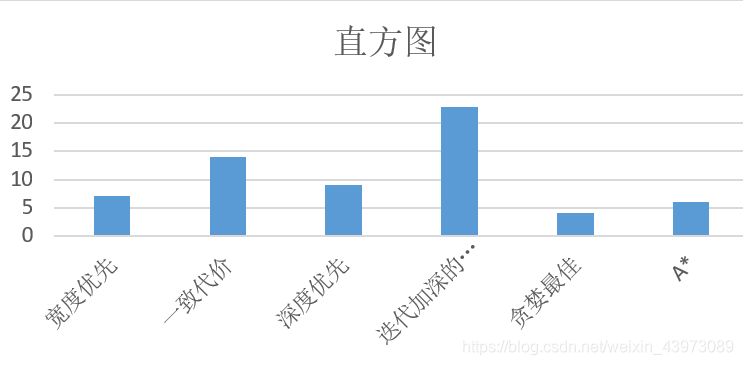

五、 思考

1、 宽度优先搜索，深度优先搜索，一致代价搜索，迭代加深的深度优先搜索算法哪种方法最优？

根据程序结果，一致代价搜索与A搜索是最优的；
一致代价搜索扩展的是当前路径代价最小的结点，对于一般性的步骤代价而言算法是最优的。A搜索因为启发式函数h满足可归纳性，因此是最优的。
此次的罗马尼亚问题规模太小，因此在时间上并不能看出太大差距，但在扩展结点的个数上可以看出一致代价搜索结点最少。

2、 贪婪最佳优先搜索和A*搜索那种方法最优？

考虑到实际问题的搜索求解时，A* 搜索算法是最优的。如果我们想要找到最小代价的解，首先扩展评估函数值最小的结点是合理；
其中，A* 搜索算法的最优性取决于：如果启发式函数是可采纳的，那么 A* 的树搜索版本是最优的，如果启发式函数是一致的，那么图搜索的 A* 算法是最优的。

3、 分析比较无信息搜索策略和有信息搜索策略。

无信息搜索指的是除了问题定义中提供的状态信息外没有任何附加信息，只是简单计算达到各个结点所需要的消耗值并比较，有信息搜索策略使用问题本身的定义之外的特定知识，比无信息的搜索策略更有效的进行问题求解。

六、 总结

此次实验让我们再次回顾了学习过的无信息搜索与有信息搜索策略。并且结合具体问题实现了这几种搜索策略，进一步加深了我对它们的理解与掌握。同时对罗马尼亚问题的求解教会了我如何将算法应用到实际问题中，受益匪浅。