贝叶斯实战

---

在scikit中有多种不同的朴素贝叶斯分类器，区别在于假设了不同$P(X^{(j)}|y=c_k)$的分布。

• GaussianNB是高斯贝叶斯分类器，假设特征的条件概率分布满足高斯分布
  $$P(X^{(j)}|y=c_k)=\frac{1}{\sqrt{2\pi {\sigma }_k^2}}\exp (-\frac{(X^{(j)}-{\mu }_k{)}^2}{2{\sigma }_k^2})$$

• MultinomialNB是多项式贝叶斯分类器，假设特征的条件概率分布满足多项式分布
  $$P(X^{(j)}=a_{sj}|y=c_k)=\frac{N_{kj}+\alpha }{N_k+\alpha n}$$
  其中，$a_{sj}$表示特征$X^{(j)}$的取值，其取值个数为$s_j$个，$N_k={\sum }_{i=1}^{N}I(y_i=c_k)$，表示属于类别$c_k$的样本的数量。$N_{kj}={\sum }_{i=1}^{N}I(y_i=c_k,X^{(j)}=a_{sj})$，表示属于类别$c_k$且特征$X^{(j)}=a_{sj}$的样本的数量，$\alpha$就是贝叶斯估计中的$\lambda$

• BernolliNB是伯努利贝叶斯分类器，假设特征的条件概率分布满足二项分布
  $$P(X^{(j)}|y=c_k)=p{X}^{(j)}+(1-p)(1-X^{(j)})$$
  其中，要求特征的取值为X(j)∈{0,1}X^{(j)}\in \{0,1\}X(j)∈{0,1}，且$P(X^{(j)}=1|y=c_k)=p$

与多项式模型一样，伯努利模型适用于离散特征的情况，不同的是，伯努利模型中每个特征的取值只能是0或1。

导入数据

from sklearn import  datasets, model_selection, naive_bayes
import  numpy as np
import matplotlib.pyplot as plt

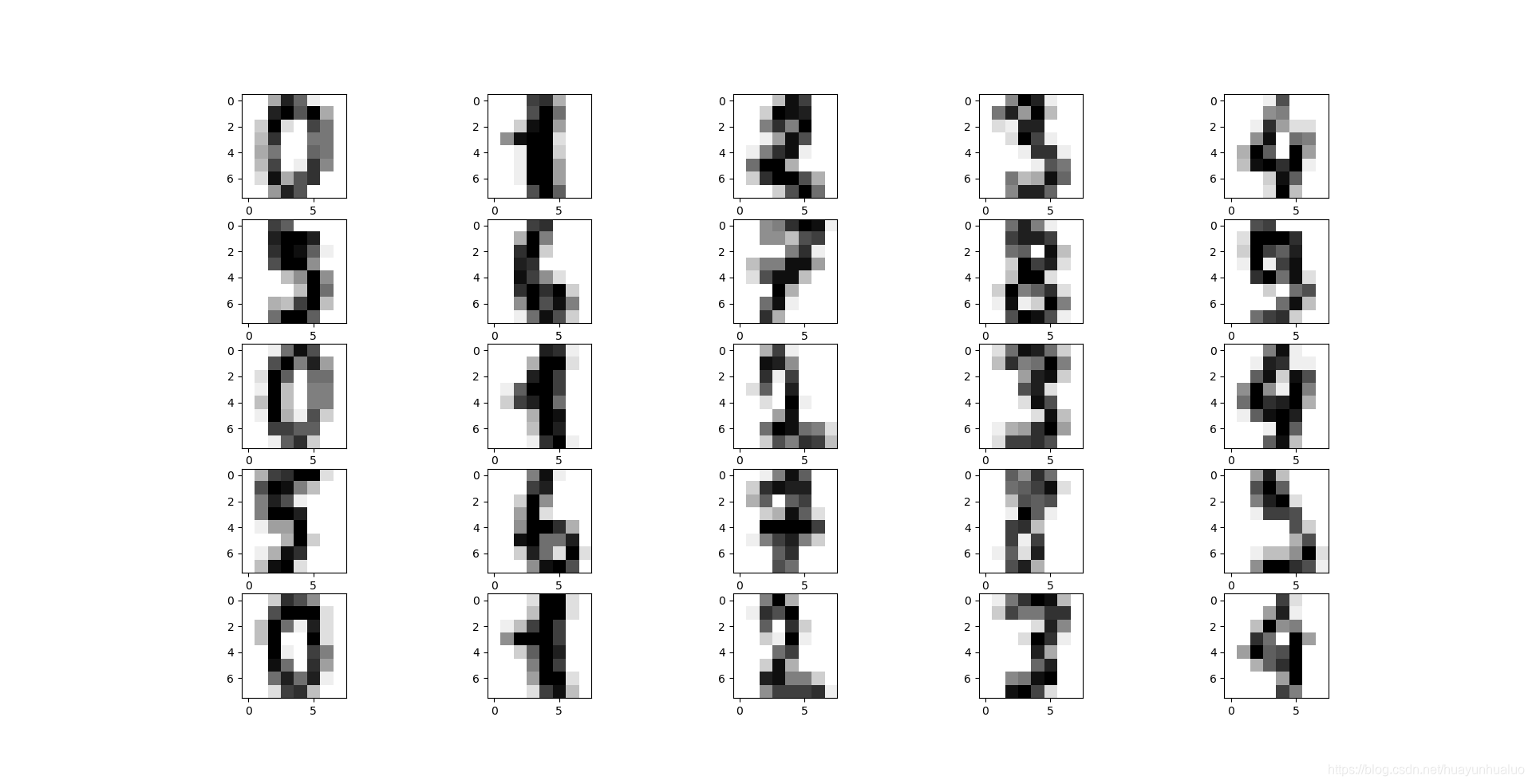
def show_digits():
    digits = datasets.load_digits()
    fig = plt.figure()
    print("vector from images 0:",digits.data[0])
    for i in range(25):
        ax = fig.add_subplot(5,5,i+1)
        ax.imshow(digits.images[i], cmap = plt.cm.gray_r, interpolation='nearest')
    plt.show()
show_digits()

vector from images 0: [ 0.  0.  5. 13.  9.  1.  0.  0.  0.  0. 13. 15. 10. 15.  5.  0.  0.  3.
 15.  2.  0. 11.  8.  0.  0.  4. 12.  0.  0.  8.  8.  0.  0.  5.  8.  0.
  0.  9.  8.  0.  0.  4. 11.  0.  1. 12.  7.  0.  0.  2. 14.  5. 10. 12.
  0.  0.  0.  0.  6. 13. 10.  0.  0.  0.]

加载数据集的函数

def load_data():
    digits = datasets.load_digits()
    return model_selection.train_test_split(digits.data,digits.target, test_size=0.25, random_state=0)

高斯贝叶斯分类器（GaussianNB）

原型

class sklearn.naive_bayes.GaussianNB()

GaussianNB没有参数，因此不需要调参

属性

• class_prior 一个数组，形状为n_classes 是每个类别的概率（$P(y=c_k)$）
• class_count 一个数组，形状为n_classes 是每个类别包含的训练样本的数量
• theta_ 一个数组，形状为(n_classes , n_features) 是每个类别上每个特征的均值${\mu }_k$
• sigma_ 一个数组，形状为(n_classes, n_features) 是每个类别上 每个特征的标准差${\sigma }_k$

def test_GuassianNB(*data):
    X_train,X_test,y_train,y_test = data
    cls = naive_bayes.GaussianNB()
    cls.fit(X_train,y_train)
    print("Training Score: %.2f" %cls.score(X_train,y_train))
    print("Testing Score: %.2f" %cls.score(X_test,y_test))

X_train, X_test, y_train,y_test = load_data()
test_GuassianNB(X_train, X_test, y_train,y_test)

运行的结果

Training Score: 0.86
Testing Score: 0.83

可以看到对训练数据集的预测准确度为86%，对测试数据集的预测准确度为83%

多项式贝叶斯分类器(MultinomialNB)

原型为

naive_bayes.MultinomiaNB(alpha=1.0, fit_prior=True, class_prior=None)

参数：

• alpha 一个浮点数，指定$\alpha$值
• fit_prior 布尔值，如果为True，则不去学习$P(y=c_k)$，代替均匀分布，如果为False，则去学习$P(y=c_k)$
• class_prior 一个数组，指定了每个分类的先验概率$P(y=c_1),P(c=c_2)\cdots P(c=c_k)$，如果指定了该参数，则每个分类的先验概率不再从数据集中学得。
• class_log_prior 一个数组对象，形状为n_classes 给出了每个类别调整后的经验概率分布的对数值

def test_MultinomiaNB(*data):
    X_train,X_test,y_train,y_test = data
    cls = naive_bayes.MultinomialNB()
    cls.fit(X_train,y_train)
    print("Training Score: %.2f" % cls.score(X_train, y_train))
    print("Testing Score: %.2f" % cls.score(X_test, y_test))

X_train, X_test, y_train,y_test = load_data()
test_MultinomiaNB(X_train, X_test, y_train,y_test)

Training Score: 0.91
Testing Score: 0.91

对训练集的预测和测试集的预测是相同的

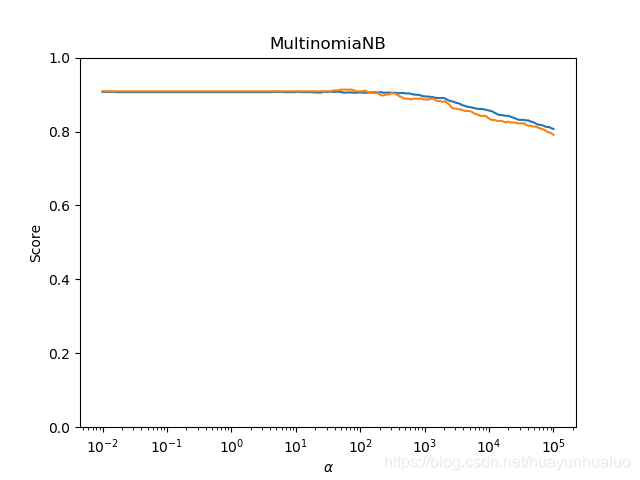
下面检测不同的$\alpha$对多项式贝叶斯分类器的预测性能的影响

def test_MultinomialNB_alpha(*data):
    X_train,X_test,y_train,y_test = data
    alphas = np.logspace(-2, 5, num=200)
    train_scores = []
    test_scores = []
    for alpha in alphas:
        cls = naive_bayes.MultinomialNB(alpha=alpha)
        cls.fit(X_train, y_train)
        train_scores.append(cls.score(X_train,y_train))
        test_scores.append(cls.score(X_test,y_test))
    # 绘图
    fig = plt.figure()
    ax = fig.add_subplot(1,1,1)
    ax.plot(alphas, train_scores, label="Training Score")
    ax.plot(alphas, test_scores, label="Testing Score")
    ax.set_xlabel(r"$\alpha$")
    ax.set_ylabel("Score")
    ax.set_ylim(0, 1.0)
    ax.set_title("MultinomiaNB")
    ax.set_xscale("log")
    plt.show()

X_train, X_test, y_train,y_test = load_data()
test_MultinomialNB_alpha(X_train, X_test, y_train,y_test)

伯努利贝叶斯分类器（BernoulliNB）

函数原型

BernoulliNB(alpha = 1.0, binarize = 0.0, fit_prior = True, class_prior = None)

参数

• alpha 一个浮点数，指定的$\alpha$值，就是贝叶斯估计中的$\lambda$
• binarize 一个浮点数或者None
  • 如果为None 那么会假定原始数据已经二元化了
  • 如果是浮点数，那么会以该数值为界，特征取值大于它的作为1，否则作为0，采取这种策略来二元化
• fit_prior 布尔值，如果是True，则不去学习$P(y=c_k)$，代替均匀分布，如果为False，则去学习
• class_prior 一个数组

def test_BernomulliNB(*data):
    X_train,X_test,y_train,y_test = data
    cls = naive_bayes.BernoulliNB()
    cls.fit(X_train,y_train)
    print("Training Score: %.2f "%cls.score(X_train,y_train))
    print("Testing Score: %.2f "%cls.score(X_test, y_test))
X_train, X_test, y_train,y_test = load_data()
test_BernomulliNB(X_train, X_test, y_train,y_test)

Training Score: 0.87 
Testing Score: 0.85 

可以看到对训练集的预测准确率更高

def test_BernoulliNB_alpha(*data):
    X_train,X_test,y_train,y_test = data
    alphas = np.logspace(-2, 5, num=200)
    train_score = []
    test_score = []
    for alpha in alphas:
        cls = naive_bayes.BernoulliNB(alpha=alpha)
        cls.fit(X_train, y_train)
        train_score.append(cls.score(X_train,y_train))
        test_score.append(cls.score(X_test, y_test))

    # 绘图
    fig = plt.figure()
    ax = fig.add_subplot(1,1,1)
    ax.plot(alphas, train_score, label="Training Score")
    ax.plot(alphas, test_score, label= "Testing Score")
    ax.set_xlabel(r"$\alpha$")
    ax.set_ylabel("Score")
    ax.set_ylim(0, 1.0)
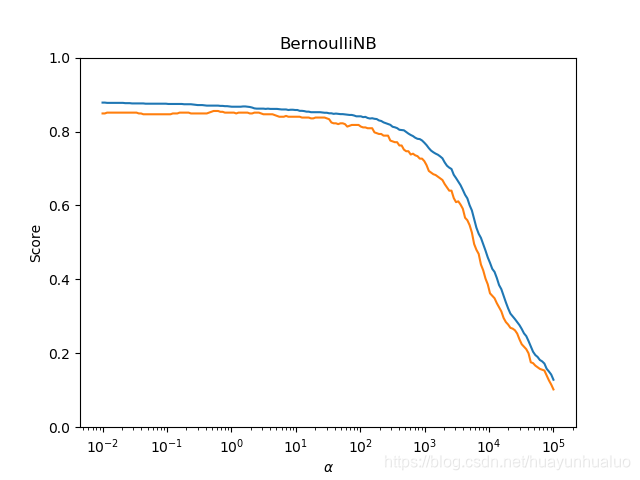
    ax.set_title("BernoulliNB")
    ax.set_xscale("log")
    ax.lengend(loc = "best")
    plt.show()

X_train, X_test, y_train,y_test = load_data()
test_BernoulliNB_alpha(X_train, X_test, y_train,y_test)