(机器学习、人工智能数学基础:高等数学篇)第二章:导数与微分:第二节:求导
导数本质:是看某个量的微小变化以及它和它所导致的另一个量的微小变化有何关系如下f(x)=x2f(x)=x^{2}f(x)=x2,该函数表示某个正方形的面积。当该正方形两边都扩展dxdxdx长度时,此时多出来的面积就会由三部分组成所以多出来的面积(面积的变化量):两个小长方形+一个小正方形,也即df=xdx+xdx+dx2df=xdx+xdx+dx^{2}df=xdx+xdx+dx2。但是你会发现后
文章目录
一:导数、求导本质
导数本质:是看某个量的微小变化以及它和它所导致的另一个量的微小变化有何关系
如下 f ( x ) = x 2 f(x)=x^{2} f(x)=x2,该函数表示某个正方形的面积。当该正方形两边都扩展 d x dx dx长度时,此时多出来的面积就会由三部分组成
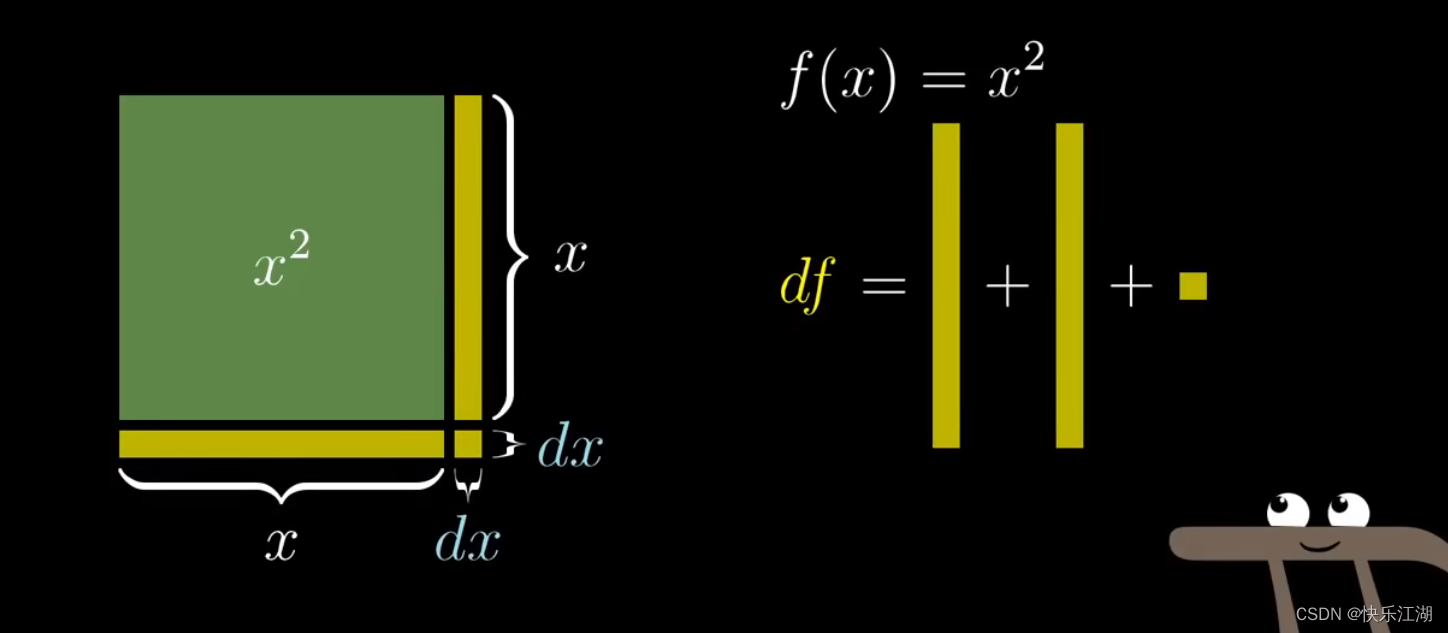
所以多出来的面积(面积的变化量):两个小长方形+一个小正方形,也即 d f = x d x + x d x + d x 2 df=xdx+xdx+dx^{2} df=xdx+xdx+dx2。但是你会发现后面的 d x 2 dx^{2} dx2实际上是可以忽略的(相对于 d x dx dx完全可以忽略不计)
因此这微小的 d x dx dx的该变量,将导致 d f df df的变化,也即 d f = 2 x d x df=2xdx df=2xdx,换个写法就是 f ( x ) = x 2 f(x)=x^{2} f(x)=x2的导数,也即 d f d x = 2 x \frac{df}{dx}=2x dxdf=2x
其实上面所忽略的部分就是高阶无穷小。例如在计算体积 f ( x ) = x 3 f(x)=x^{3} f(x)=x3时,高阶项就可以忽略不计
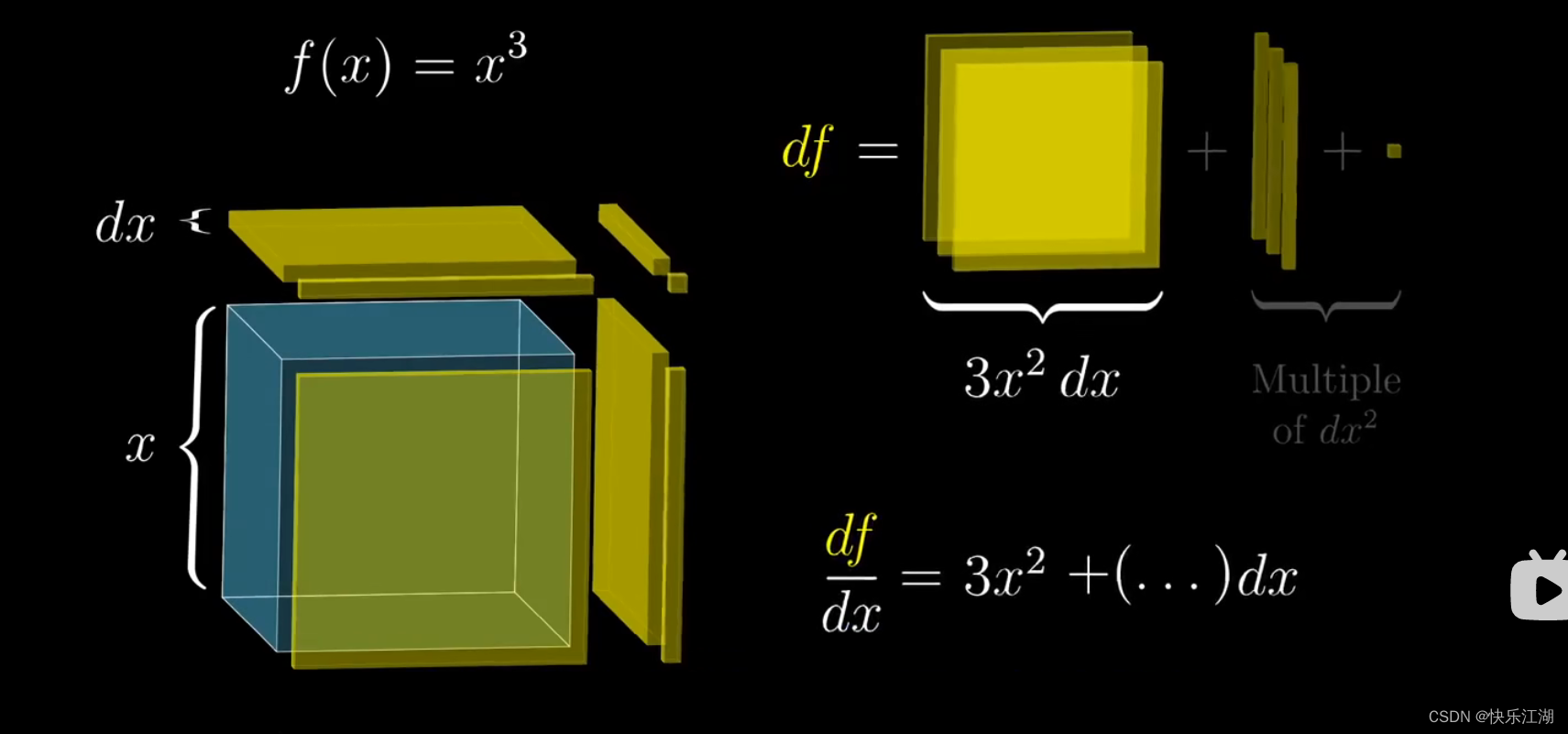
二:理解链式法则和乘积法则
- 注意:这部分非常重要,后续机器学习中公式推导严重依赖于这部分内容
(1)加法
两个函数和的导数就等于他们导数的和
如下,以 f ( x ) = s i n ( x ) + x 2 f(x)=sin(x)+x^{2} f(x)=sin(x)+x2为例
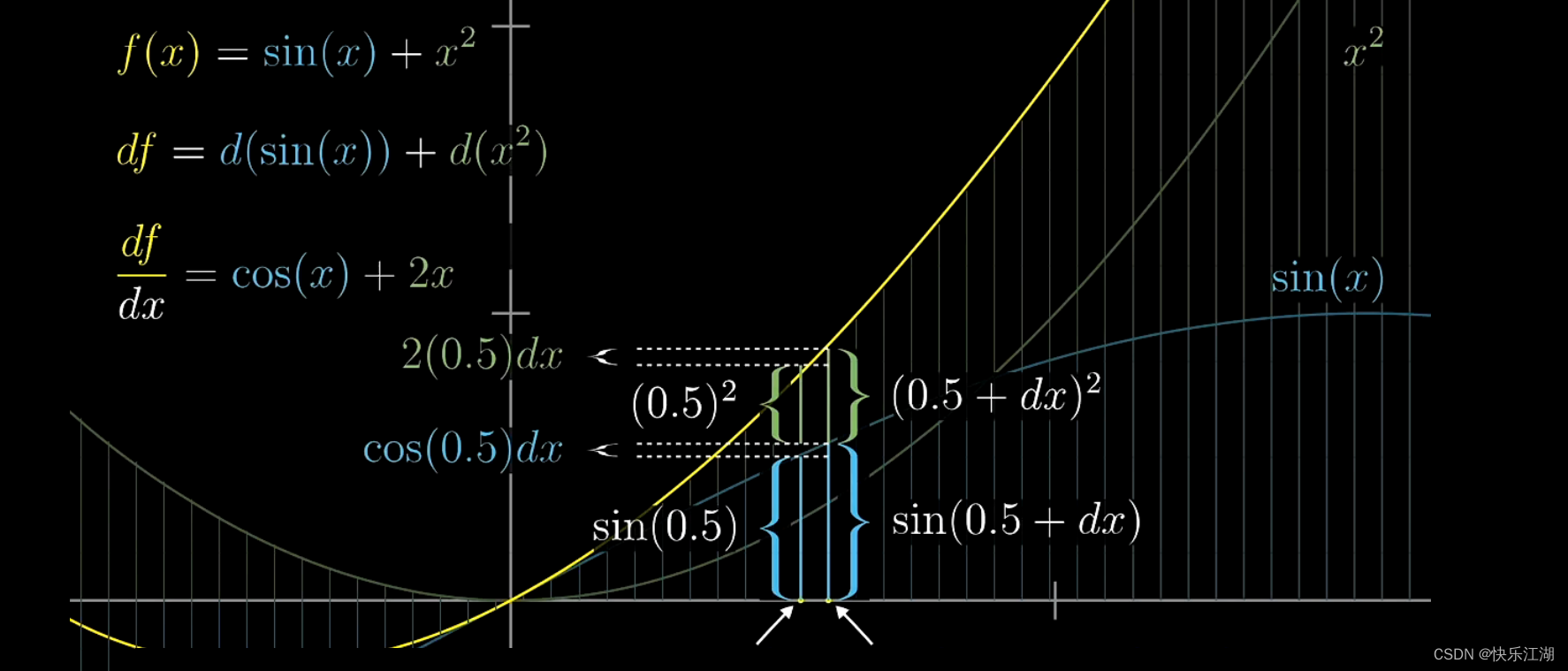
(2)乘法
如下,使用 f ( x ) = s i n ( x ) + x 2 f(x)=sin(x)+x^{2} f(x)=sin(x)+x2表示一个矩形的面积,变长的大小都取决 x x x
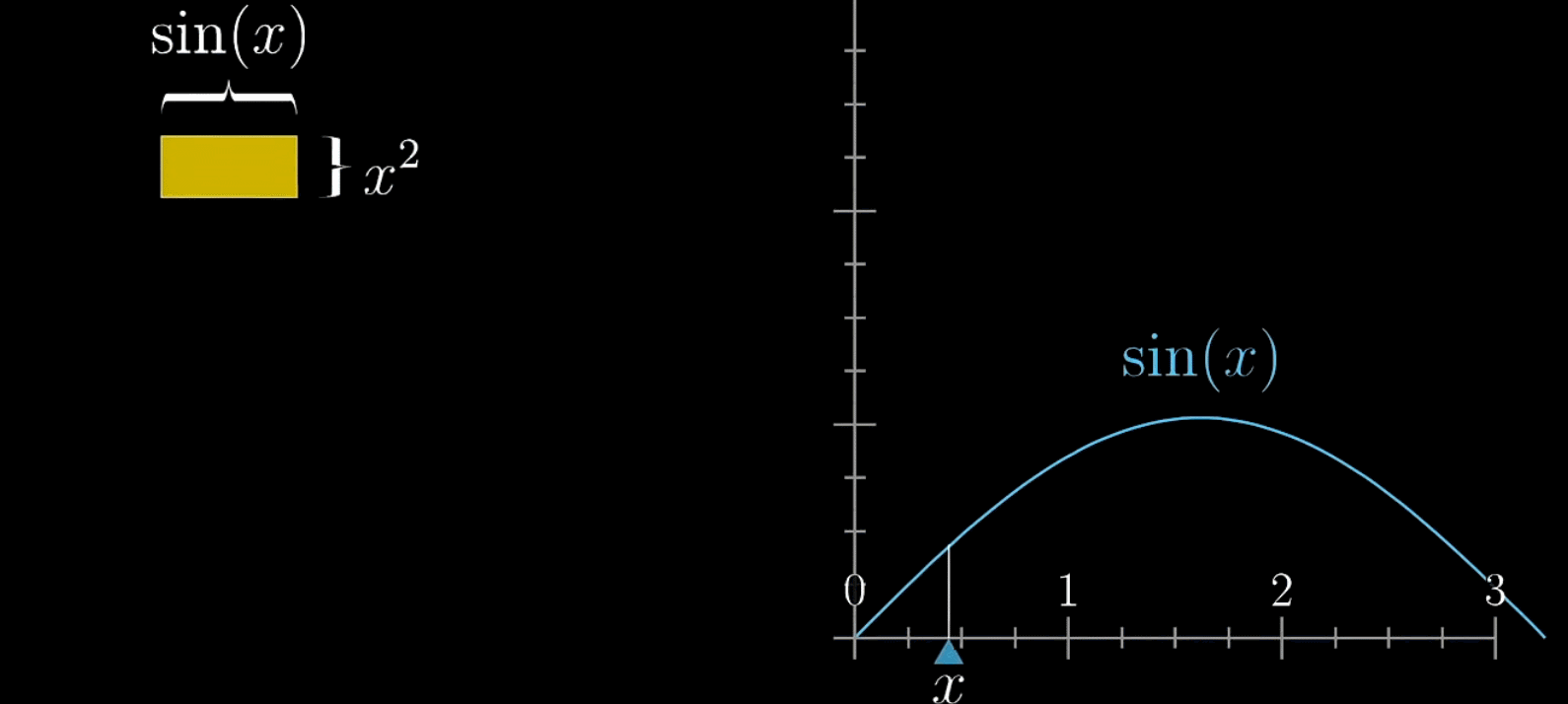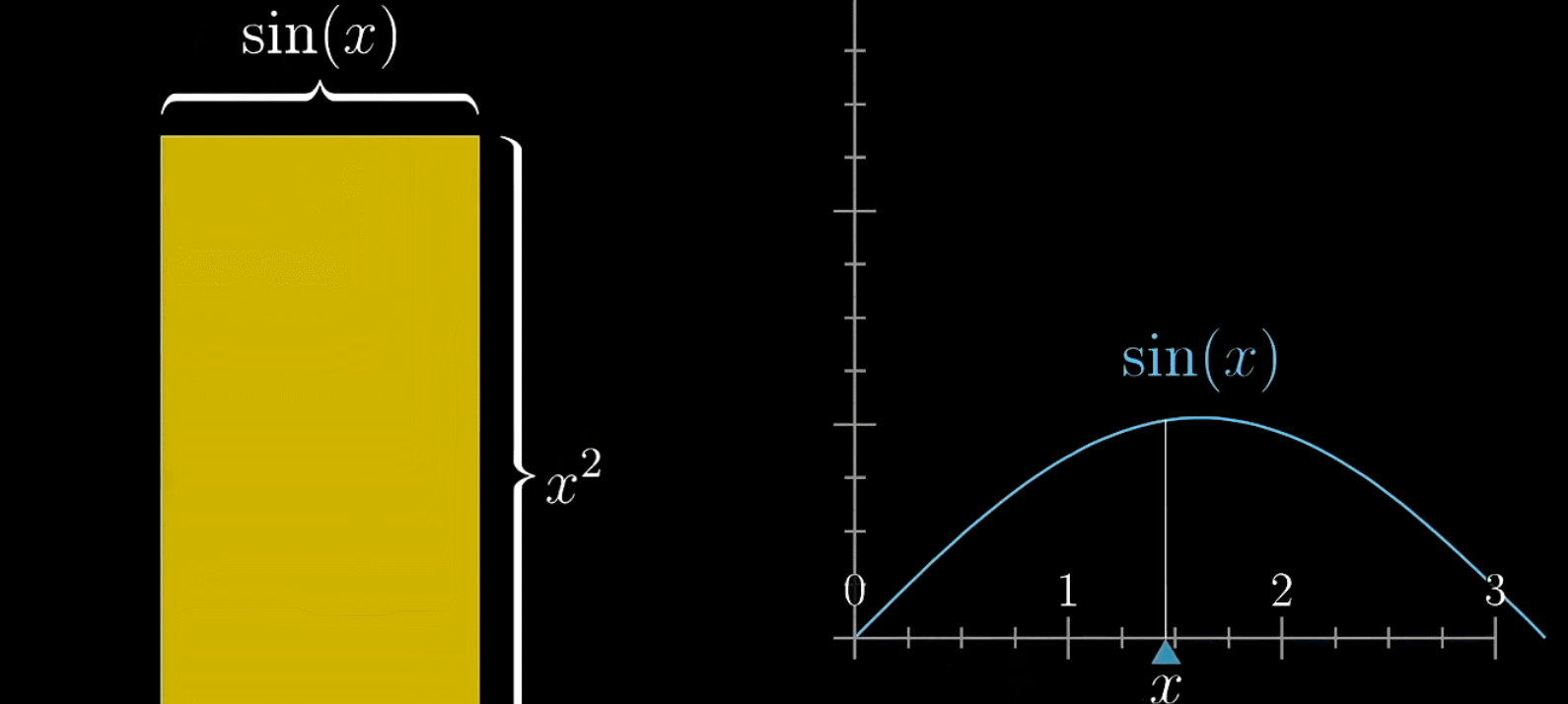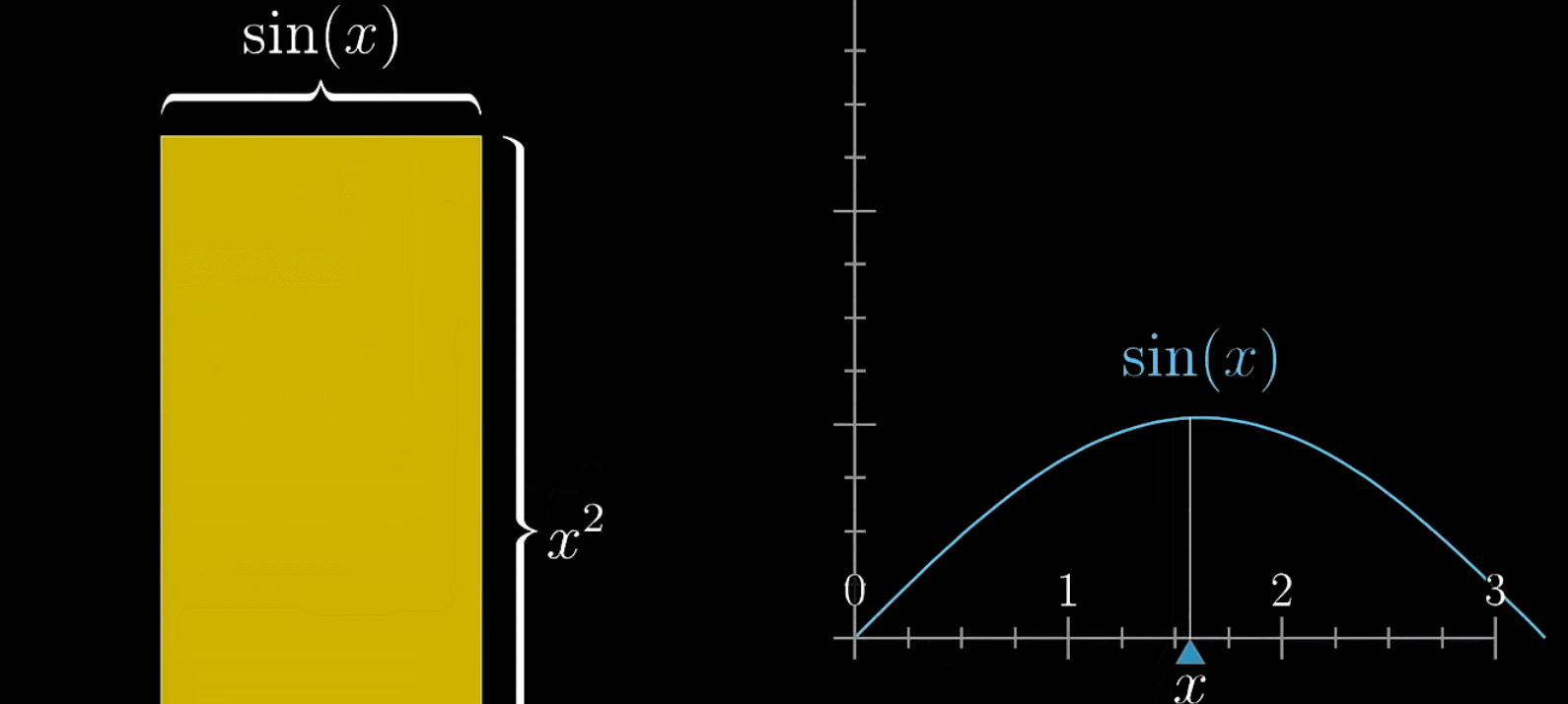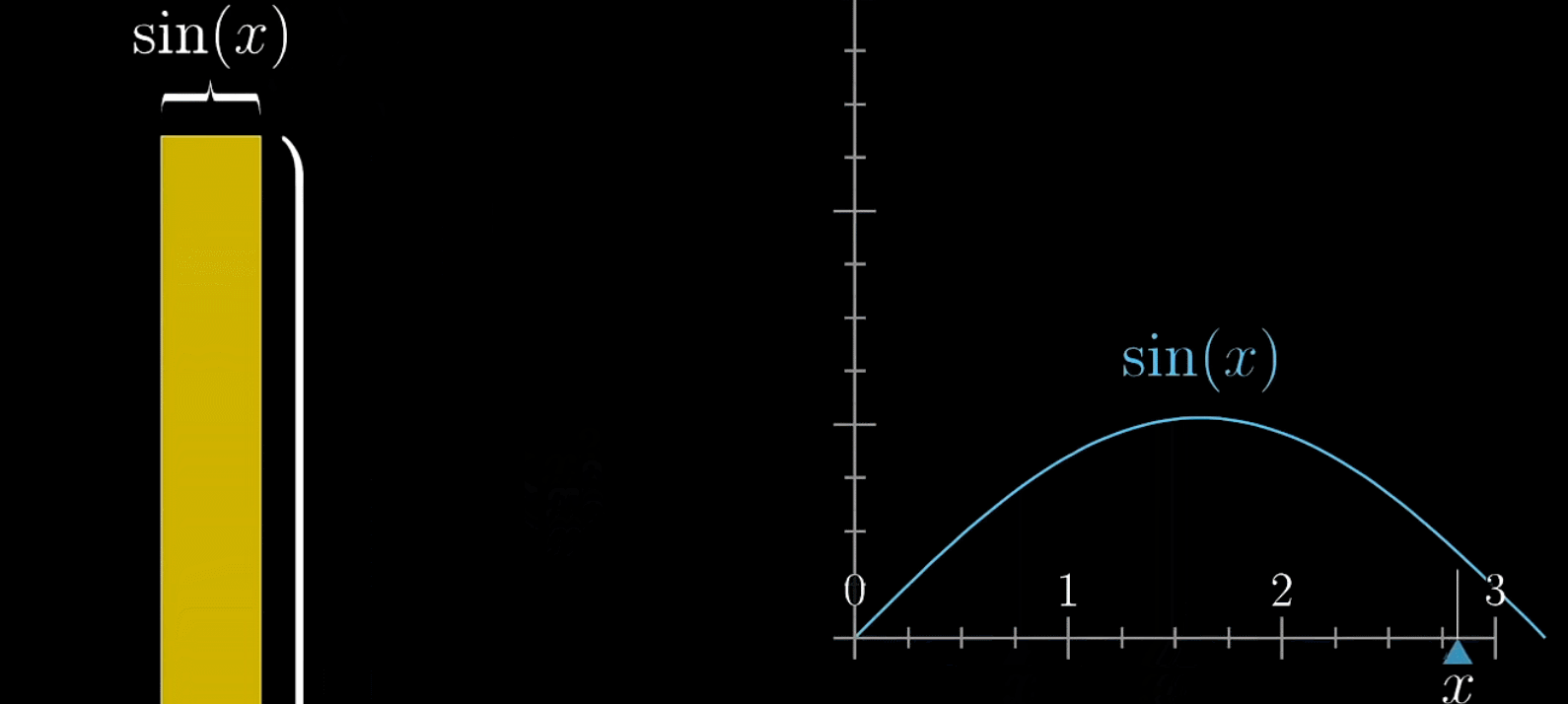
还是采用之前的分析方法,假设 x x x有一变化 d x dx dx,那么所引起的面积变化为
d f = s i n ( x ) d ( x 2 ) + x 2 d ( s i n ( x ) ) df=sin(x)d(x^{2})+x^{2}d(sin(x)) df=sin(x)d(x2)+x2d(sin(x))

继续推导,可得结果
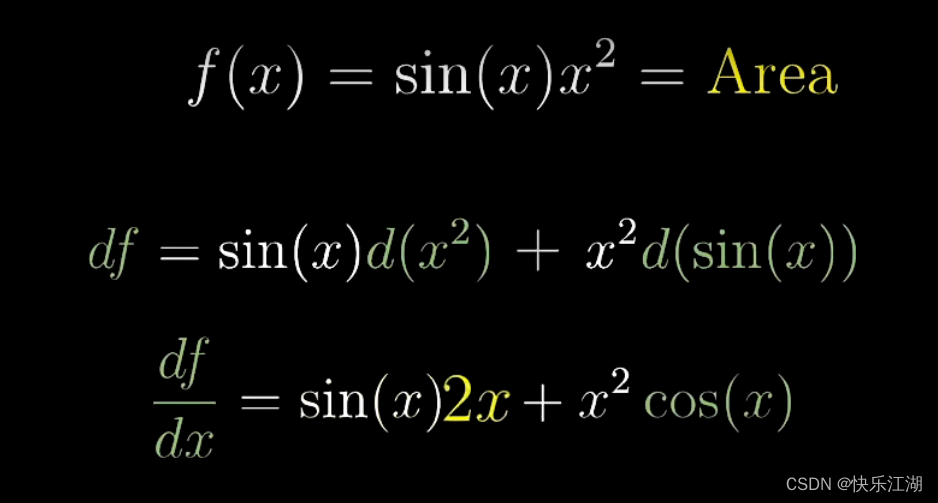
(3)复合函数
采用链式法则计算
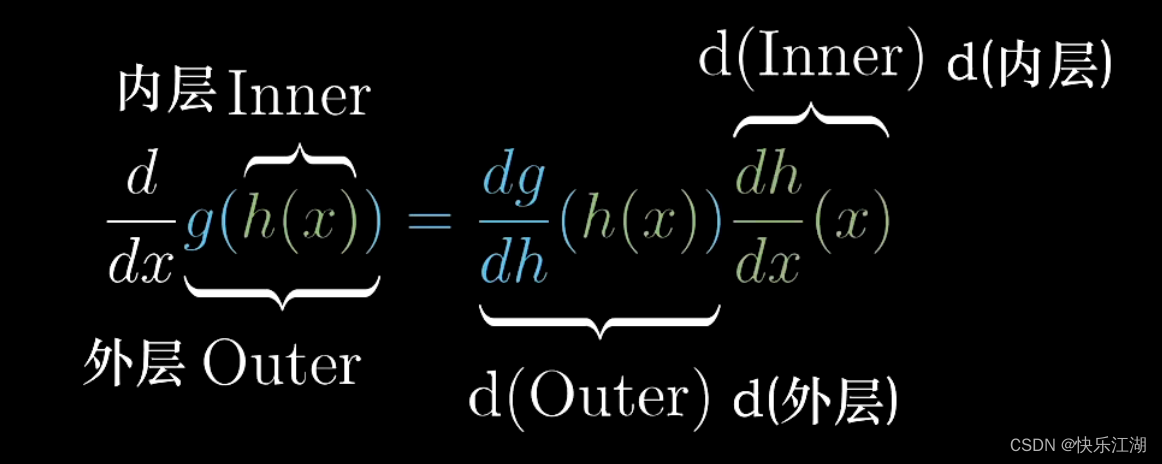
例如 f ( x ) = s i n ( x 2 ) f(x)=sin(x^{2}) f(x)=sin(x2)
d ( s i n ( x 2 ) ) = d ( s i n ( h ) ) = c o s ( h ) d h = c o s ( x 2 ) d ( x 2 ) = 2 x c o s ( x 2 ) d x d(sin(x^{2}))=d(sin(h))=cos(h)dh=cos(x^{2})d(x^{2})=2xcos(x^{2})dx d(sin(x2))=d(sin(h))=cos(h)dh=cos(x2)d(x2)=2xcos(x2)dx
三:基本初等函数的导数公式
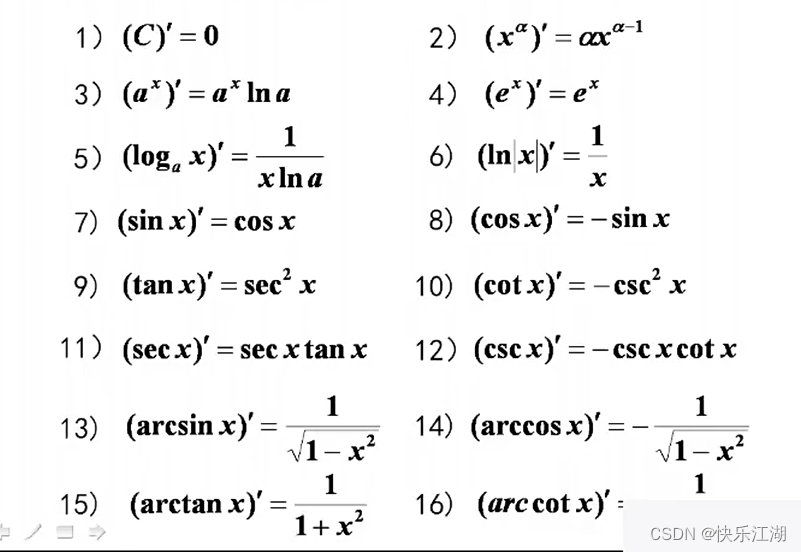
四:求导法则
(1)有理函数运算法则
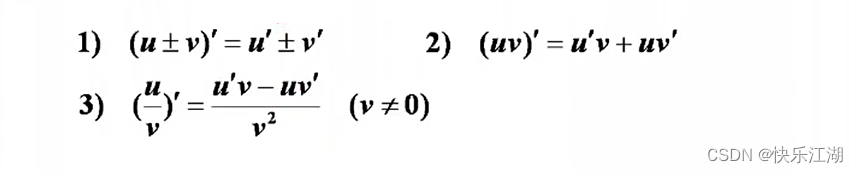
(2)复合函数求导
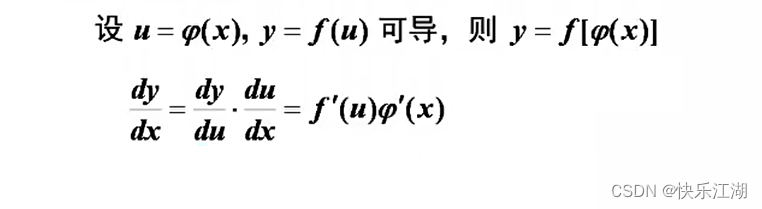
(3)隐函数求导
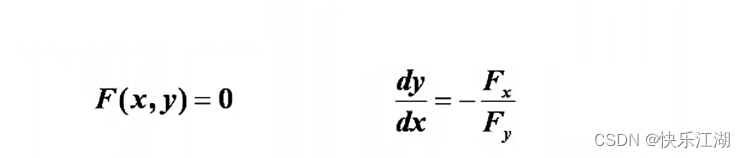
(4)反函数求导

(5)参数方程求导
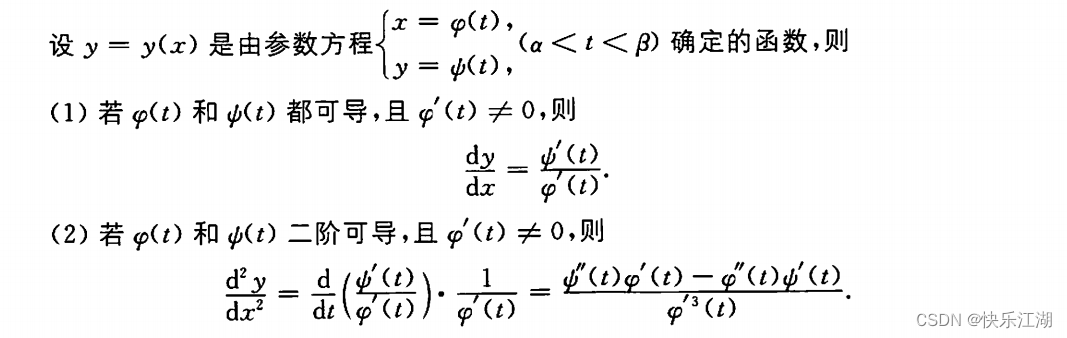
(6)对数求导

五:高阶导数
高阶导定义

- 如果函数 f ( x ) f(x) f(x)在点 x x x处 n n n阶可导,则在点 x x x的某邻域内 f ( x ) f(x) f(x)必定具有
一切低于 n n n阶的倒数
常用高阶导公式
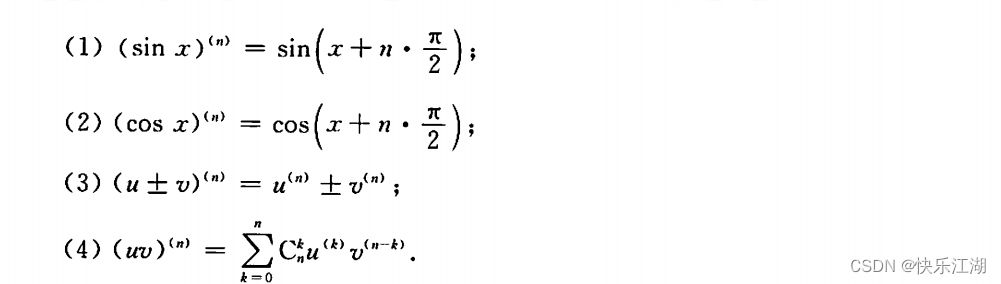
更多推荐
 已为社区贡献3条内容
已为社区贡献3条内容










所有评论(0)