RNN (循环神经网络 - 从mlp到rnn - 困惑度 - 梯度剪裁) + 代码实现 —— 笔记3.4《动手学深度学习》
我们在本节中会训练一个基于循环神经网络的字符级语言模型,根据用户提供的文本的前缀生成后续文本。一个简单的循环神经网络语言模型包括输入编码、循环神经网络模型和输出生成。循环神经网络模型在训练以前需要初始化状态,不过随机抽样和顺序划分使用初始化方法不同。当使用顺序划分时,我们需要分离梯度以减少计算量。在进行任何预测之前,模型通过预热期进行自我更新(例如,获得比初始值更好的隐状态)。梯度裁剪可以防止梯度
目录
0. 前言
- 课程全部代码(pytorch版)已上传到附件
- 看懂本篇RNN的所有细节,后面的GRU、LSTM甚至注意力机制都能容易理解,因为RNN是一切序列模型的基础
- 本章节为原书第8章(循环神经网络),共分为7节,本篇是第4-6节:
- RNN
- RNN 从零实现
- RNN 简洁实现
- 本篇(4-6节)的代码位置为:
- chapter_recurrent-neural-networks/rnn.ipynb
- chapter_recurrent-neural-networks/rnn-scratch.ipynb
- chapter_recurrent-neural-networks/rnn-concise.ipynb
- 本篇(4-6节)的视频链接:

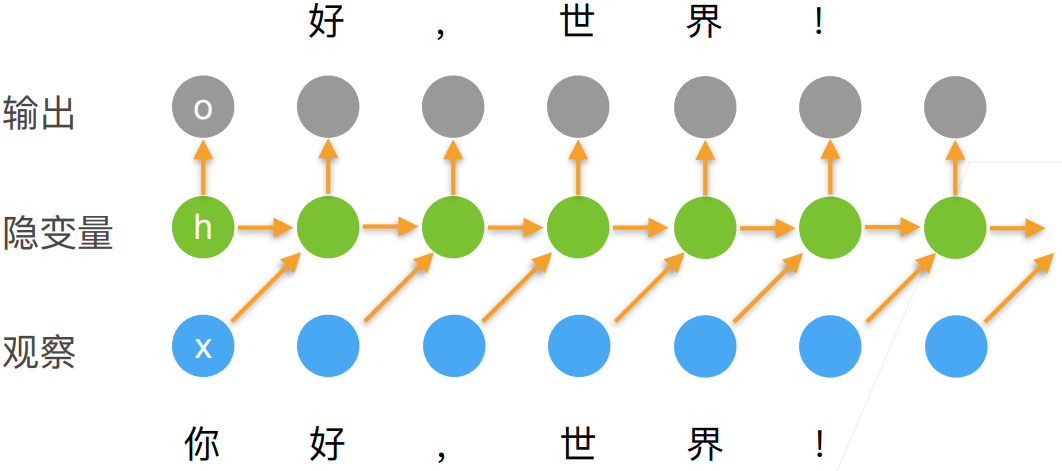
1. RNN 的基础概念

:eqlabel:eq_ht_xt
对于 :eqref:eq_ht_xt中的函数𝑓,隐变量模型不是近似值。 毕竟ℎ𝑡是可以仅仅存储到目前为止观察到的所有数据, 然而这样的操作可能会使计算和存储的代价都变得昂贵。
回想一下,我们在 :numref:chap_perceptrons中 讨论过的具有隐藏单元的隐藏层。 值得注意的是,隐藏层和隐状态指的是两个截然不同的概念。 如上所述,隐藏层是在从输入到输出的路径上(以观测角度来理解)的隐藏的层, 而隐状态则是在给定步骤所做的任何事情(以技术角度来定义)的输入, 并且这些状态只能通过先前时间步的数据来计算。
循环神经网络(recurrent neural networks,RNNs) 是具有隐状态的神经网络。 在介绍循环神经网络模型之前, 我们首先回顾 :numref:sec_mlp中介绍的多层感知机模型。
1.1 无隐状态的单层MLP

补充1:单隐藏层的MLP
- 每个箭头都对应一个独立参数
- 每1个参数按照输入维度作为行,输出维度作为列,组成一个矩阵
- 能够方便计算机做感知机的前向传播和反向传播
- 输入层 - 2维向量X;x=2
- 隐藏层(第一层) - ReLU层 (3个神经元);h = 3
- 隐层参数:输入2x输出3=6个参数
- 输出层(第二层) - Softmax层 (2个神经元, 二元分类);q=2
- 输出层参数:输入3x输出2=6个参数
- X∈
:输入X的形状是n×d
- n:批量大小batch size (一个小批量mini batch里有几个样本)
- d:输入的维度,在上图案例中是2维
- H的形状是n×h,h是该隐层神经元数量
这完全类似于之前在 :numref:sec_sequence中解决的回归问题, 因此我们省略了细节。 无须多言,只要可以随机选择“特征-标签”对, 并且通过自动微分和随机梯度下降能够学习网络参数就可以了。
1.2 有隐状态的RNN
:label:subsec_rnn_w_hidden_states
 保留了序列直到其当前时间步的历史信息, 就如当前时间步下神经网络的状态或记忆, 因此这样的隐藏变量被称为隐状态(hidden state)。 由于在当前时间步中, 隐状态使用的定义与前一个时间步中使用的定义相同, 因此 :eqref:
保留了序列直到其当前时间步的历史信息, 就如当前时间步下神经网络的状态或记忆, 因此这样的隐藏变量被称为隐状态(hidden state)。 由于在当前时间步中, 隐状态使用的定义与前一个时间步中使用的定义相同, 因此 :eqref:rnn_h_with_state的计算是循环的(recurrent)。 于是基于循环计算的隐状态神经网络被命名为 循环神经网络(recurrent neural network)。 在循环神经网络中执行 :eqref:rnn_h_with_state计算的层 称为循环层(recurrent layer)。
有许多不同的方法可以构建循环神经网络, 由 :eqref:rnn_h_with_state定义的隐状态的循环神经网络是非常常见的一种。 对于时间步𝑡,输出层的输出类似于多层感知机中的计算:

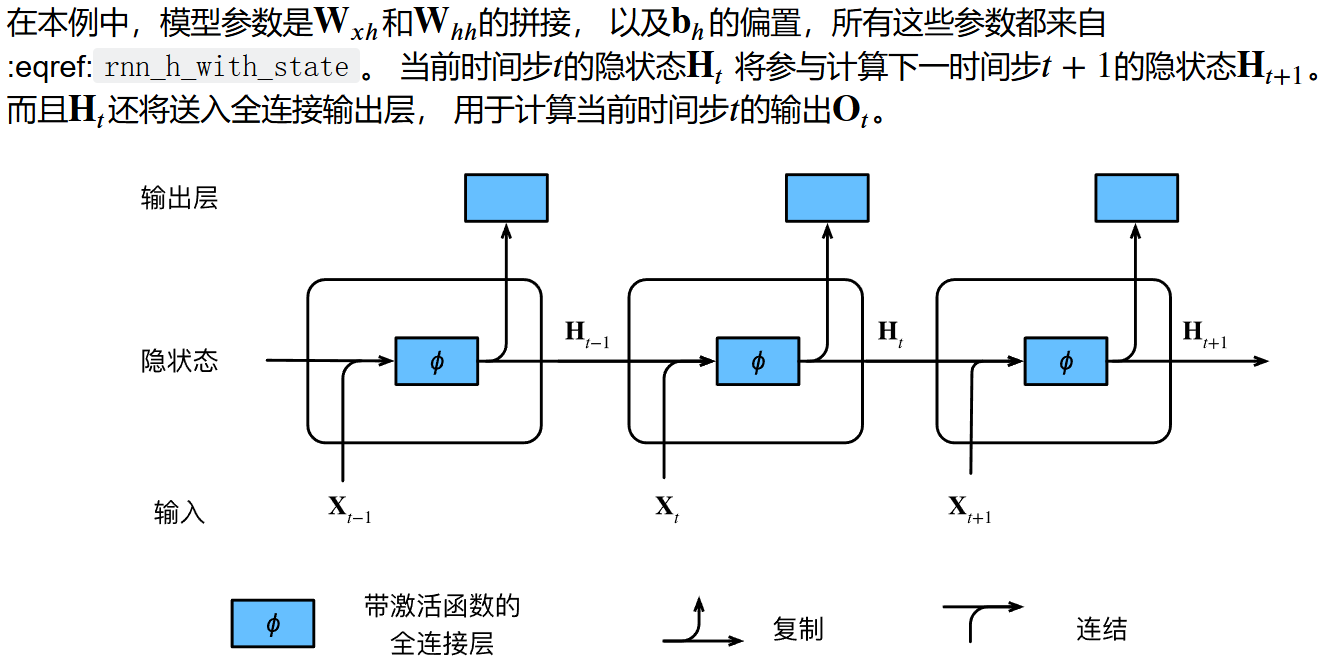 :label:
:label:fig_rnn

In [1]:
import torch
from d2l import torch as d2l
X, W_xh = torch.normal(0, 1, (3, 1)), torch.normal(0, 1, (1, 4))
H, W_hh = torch.normal(0, 1, (3, 4)), torch.normal(0, 1, (4, 4))
torch.matmul(X, W_xh) + torch.matmul(H, W_hh) # 从零实现就用这个,俩个小矩阵分别矩阵乘法Out[2]:
tensor([[-0.8178, -1.5802, 0.9147, -1.8484],
[-1.2241, -1.5641, 0.4927, 0.6111],
[ 2.2942, -1.4934, 1.5947, 1.3788]])
现在,我们沿列(轴1)拼接矩阵X和H, 沿行(轴0)拼接矩阵W_xh和W_hh。 这两个拼接分别产生形状(3,5)和形状(5,4)的矩阵。 再将这两个拼接的矩阵相乘, 我们得到与上面相同形状(3,4)的输出矩阵。
In [3]:
torch.matmul(torch.cat((X, H), 1), torch.cat((W_xh, W_hh), 0)) # 用pytorch框架(简洁实现)就用这个,快3-4倍
# 一个大矩阵比多个小矩阵,做并行计算的开销要小很多Out[3]:
tensor([[-0.8178, -1.5802, 0.9147, -1.8484],
[-1.2241, -1.5641, 0.4927, 0.6111],
[ 2.2942, -1.4934, 1.5947, 1.3788]])
1.3 用RNN建(语言)模(型) - 重要
回想一下 :numref:sec_language_model中的语言模型, 我们的目标是根据过去的和当前的词元预测下一个词元, 因此我们将原始序列移位一个词元作为标签。 Bengio等人首先提出使用神经网络进行语言建模 :cite:Bengio.Ducharme.Vincent.ea.2003。 接下来,我们看一下如何使用循环神经网络来构建语言模型。 设小批量大小为1,批量中的文本序列为“machine”。 为了简化后续部分的训练,我们考虑使用 字符级语言模型(character-level language model), 将文本词元化为字符而不是单词。 :numref:fig_rnn_train演示了 如何通过基于字符级语言建模的循环神经网络, 使用当前的和先前的字符预测下一个字符。
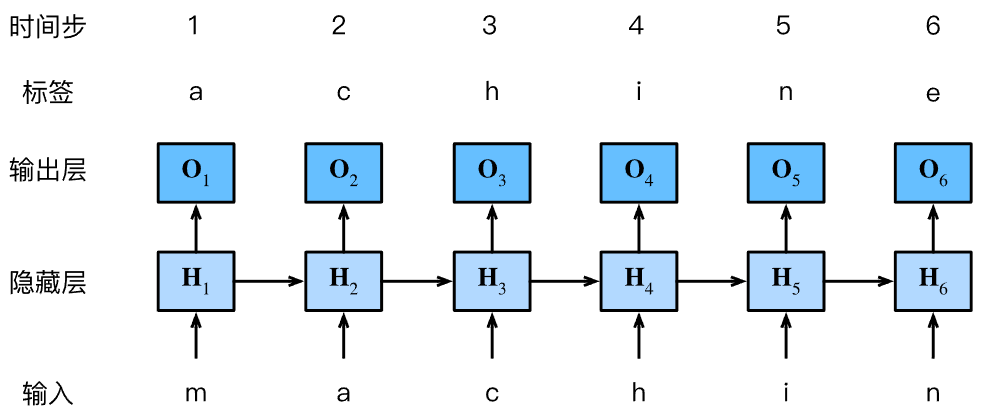
:label:fig_rnn_train
在训练过程中,我们对每个时间步的输出层的输出进行softmax操作, 然后利用交叉熵损失计算模型输出和标签之间的误差。 由于隐藏层中隐状态的循环计算, :numref:fig_rnn_train中的第3个时间步的输出由文本序列“m”“a”和“c”确定。 由于训练数据中这个文本序列的下一个字符是“h”, 因此第3个时间步的损失将取决于下一个字符的概率分布, 而下一个字符是基于特征序列“m”“a”“c”和这个时间步的标签(标准答案)“h”生成的。
在实践中,我们使用的批量大小为𝑛>1, 每个mini batch(形状是n×d)中的每个样本(形状是(1,d),d个词元token)由一个𝑑维向量(若将将词元序列看作一个马尔科夫链,那么d维向量对应着马尔科夫假设中的tau个时间步)表示。 因此,在时间步𝑡输入将是一个𝑛×𝑑矩阵, 这与我们在 :numref:
subsec_rnn_w_hidden_states中的讨论相同。
1.4 困惑度 (Perplexity)
:label:subsec_perplexity
最后,让我们讨论如何度量语言模型的质量, 这将在后续部分中用于评估基于循环神经网络的模型。 一个好的语言模型能够用高度准确的词元来预测我们接下来会看到什么。 考虑一下由不同的语言模型给出的对“It is raining ...”(“...下雨了”)的续写:
- "It is raining outside"(外面下雨了);
- "It is raining banana tree"(香蕉树下雨了);
- "It is raining piouw;kcj pwepoiut"(piouw;kcj pwepoiut下雨了)。
就质量而言,例1显然是最合乎情理、在逻辑上最连贯的。 虽然这个模型可能没有很准确地反映出后续词的语义, 比如,“It is raining in San Francisco”(旧金山下雨了) 和“It is raining in winter”(冬天下雨了) 可能才是更完美的合理扩展, 但该模型已经能够捕捉到跟在后面的是哪类单词。 例2则要糟糕得多,因为其产生了一个无意义的续写。 尽管如此,至少该模型已经学会了如何拼写单词, 以及单词之间的某种程度的相关性。 最后,例3表明了训练不足的模型是无法正确地拟合数据的。
我们可以通过计算序列的似然概率来度量模型的质量。
补充2:似然概率
- 定义:在给定模型参数的情况下,观察到特定数据序列的概率
- 例子:假设单词之间是独立的,所以 “我爱” 的似然概率 L = P(我) x P(爱) = 0.4 x 0.3 = 0.12
然而这是一个难以理解、难以比较的数字。 毕竟,较短的序列比较长的序列更有可能出现, 因此评估模型产生托尔斯泰的巨著《战争与和平》的可能性 不可避免地会比产生圣埃克苏佩里的中篇小说《小王子》可能性要小得多。 而缺少的可能性值相当于平均数。
在这里,信息论可以派上用场了。 我们在引入softmax回归 ( :numref:subsec_info_theory_basics)时定义了熵、惊异和交叉熵, 并在信息论的在线附录 中讨论了更多的信息论知识。 如果想要压缩文本,我们可以根据当前词元集预测的下一个词元。 一个更好的语言模型应该能让我们更准确地预测下一个词元。 因此,它应该允许我们在压缩序列时花费更少的比特。 所以我们可以通过一个序列中所有的𝑛个词元的交叉熵损失的平均值来衡量:

困惑度的最好的理解是“下一个词元的实际选择数的调和平均数”。 我们看看一些案例。
- 在最好的情况下,模型总是完美地估计标签词元的概率为1。 在这种情况下,模型的困惑度为1。
- 在最坏的情况下,模型总是预测标签词元的概率为0。 在这种情况下,困惑度是正无穷大。
- 在基线上,该模型的预测是词表的所有可用词元上的均匀分布。 在这种情况下,困惑度等于词表中唯一词元的数量。 事实上,如果我们在没有任何压缩的情况下存储序列, 这将是我们能做的最好的编码方式。 因此,这种方式提供了一个重要的上限, 而任何实际模型都必须超越这个上限。
补充3:调和平均 & 均匀分布
- 这里的P可以等价于一排条件概率的乘积,可回顾语言模型小节
- 调和平均:
;在本文的例子中,指的是能将很多0-1之间的概率 (公式中的x12...n) 分别取倒数求和后,用 n (有多少个x) 做分子,算出的结果还在0-1之间
- 均匀分布:设随机变量X取值范围是
;在本文的例子中,指的是词表中每个token的词频相等
在接下来的小节中,我们将基于循环神经网络实现字符级语言模型(many to many), 并使用困惑度来评估这样的模型。
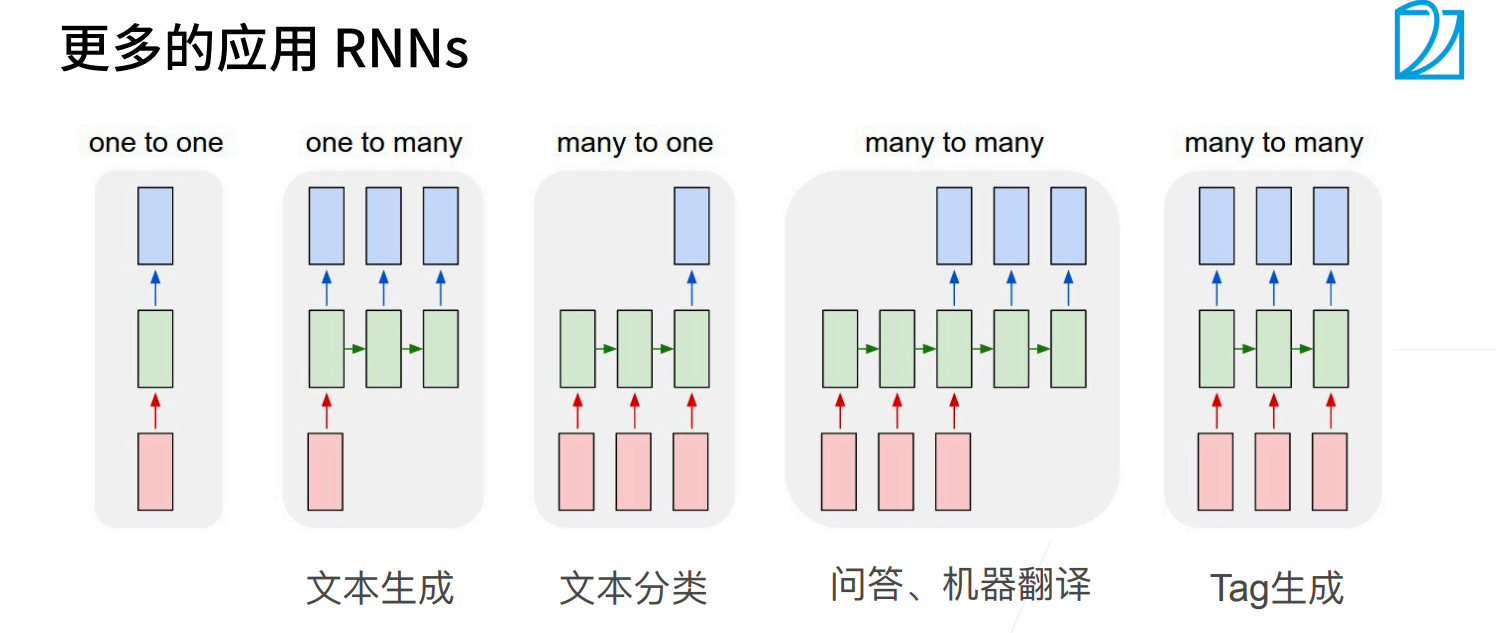
1.5 更多的RNN任务
1.6 小结
- 对隐状态使用循环计算的神经网络称为循环神经网络(RNN)。
- 循环神经网络的隐状态可以捕获直到当前时间步序列的历史信息。
- 循环神经网络模型的参数数量不会随着时间步的增加而增加。
- 我们可以使用循环神经网络创建字符级语言模型。
- 我们可以使用困惑度来评价语言模型的质量。
2. RNN 的从零实现
本节将根据 :numref:sec_rnn中的描述, 从头开始基于循环神经网络实现字符级语言模型。 这样的模型将在H.G.Wells的时光机器数据集上训练。 和前面 :numref:sec_language_model中介绍过的一样, 我们先读取数据集。
In [1]:
%matplotlib inline
import math
import torch
from torch import nn
from torch.nn import functional as F
from d2l import torch as d2lIn [2]:
batch_size, num_steps = 32, 35 # 对应上一节中的输入X:n个batch和d维向量(时间步数);num_steps一般用T表示
train_iter, vocab = d2l.load_data_time_machine(batch_size, num_steps) # 返回迭代器和词表2.1 独热编码
回想一下,在train_iter中,每个词元都表示为一个数字索引, 将这些索引直接输入神经网络可能会使学习变得困难。 我们通常将每个词元表示为更具表现力的特征向量。 最简单的表示称为独热编码(one-hot encoding), 它在 :numref:subsec_classification-problem中介绍过。
简言之,将每个索引映射为相互不同的单位向量: 假设词表中不同词元的数目为𝑁𝑁(即len(vocab)), 词元索引的范围为0到𝑁−1。 如果词元的索引是整数𝑖𝑖, 那么我们将创建一个长度为𝑁的全0向量, 并将第𝑖𝑖处的元素设置为1。 此向量是原始词元的一个独热向量。 索引为0和2的独热向量如下所示:
In [3]:
F.one_hot(torch.tensor([0, 2]), len(vocab)) # 传入一个下标,就能转成一个词表长度的向量Out[3]:
tensor([[1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0],
[0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0]])
我们每次采样的(小批量数据形状是二维张量: (批量大小,时间步数)。) one_hot函数将这样一个小批量数据转换成三维张量, 张量的最后一个维度等于词表大小(len(vocab))。 我们经常转换输入的维度,以便获得形状为 (时间步数,批量大小,词表大小)的输出。 这将使我们能够更方便地通过最外层的维度, 一步一步地更新小批量数据的隐状态。
In [4]:
X = torch.arange(10).reshape((2, 5)) # 使用独热编码后, 模型参数量会增加,但多个输出才能用感知机做分类
F.one_hot(X.T, 28).shape # X.T做转置,把时间步维度拿到前面,为了for循环每次拿同一个时间步出来做小批量Out[4]:
torch.Size([5, 2, 28])
2.2 初始化模型参数
接下来,我们[初始化循环神经网络模型的模型参数]。 隐藏单元数num_hiddens是一个可调的超参数。 当训练语言模型时,输入和输出来自相同的词表。 因此,它们具有相同的维度,即词表的大小。
In [5]:
def get_params(vocab_size, num_hiddens, device): # 初始化rnn的模型参数,并返回
num_inputs = num_outputs = vocab_size # 输入&预测的token数,即多分类问题
def normal(shape): # 给一个shape, 初始化一个均值为0方差为1的tensor
return torch.randn(size=shape, device=device) * 0.01 # 乘以0.01做(等比例)缩放,方差变为0.01
# 隐藏层参数
W_xh = normal((num_inputs, num_hiddens)) # 形状是x×h的均值为0,方差为1的tensor
W_hh = normal((num_hiddens, num_hiddens)) # rnn多了这一行W_hh的定义,这是rnn和mlp在模型定义层面的唯一区别
b_h = torch.zeros(num_hiddens, device=device)
# 输出层参数
W_hq = normal((num_hiddens, num_outputs))
b_q = torch.zeros(num_outputs, device=device)
# 附加梯度
params = [W_xh, W_hh, b_h, W_hq, b_q] # 放在一个list里
for param in params:
param.requires_grad_(True) # 告诉torch每个参数都要算梯度
return params2.3 RNN模型定义 (前向传播)
为了定义循环神经网络模型, 我们首先需要[一个init_rnn_state函数在初始化时返回隐状态]。 这个函数的返回是一个张量,张量全用0填充, 形状为(批量大小,隐藏单元数)。 在后面的章节中我们将会遇到隐状态包含多个变量的情况, 而使用元组可以更容易地处理些。
In [6]:
def init_rnn_state(batch_size, num_hiddens, device): # 初始化隐藏状态
return (torch.zeros((batch_size, num_hiddens), device=device), )
# 把返回做成元组tuple,为了后续LSTM会有2个隐变量(就有2个返回值),cnn只有一个,为了后续train函数的泛用性[下面的rnn函数定义了如何在一个时间步内计算隐状态和输出。] 循环神经网络模型通过inputs最外层的维度实现循环, 以便逐时间步更新小批量数据的隐状态H。 此外,这里使用tanh函数作为激活函数。 如 :numref:sec_mlp所述, 当元素在实数上满足均匀分布时,tanh函数的平均值为0。
In [7]:
def rnn(inputs, state, params): # 在一个时间步内计算隐状态和输出;state是长为1个元素的隐层数量
# inputs的形状:(时间步数量,批量大小,词表大小); 是3d的tensor,到这里时input已经做了转置,时间步数维提前
W_xh, W_hh, b_h, W_hq, b_q = params # 展开参数(list): params
H, = state # 因为state是一个tuple
outputs = []
# X的形状:(批量大小,词表vocab大小)
for X in inputs: # 给input做了转置后,每个X就对应同一个时间步 # 只是比mlp多了一项:torch.mm(H, W_hh)
H = torch.tanh(torch.mm(X, W_xh) + torch.mm(H, W_hh) + b_h) # 前向传播的核心公式,mm做矩阵乘法
Y = torch.mm(H, W_hq) + b_q # 拿隐状态做输出Y;Y的形状是(批量大小,词表大小),词表多大就是分多少类
outputs.append(Y) # 是for loop(循环),把每个时间步的输出Y按顺序拼接成outputs(是list)
# 最后outputs的形状是(时间步数量,批量大小,词表大小)
return torch.cat(outputs, dim=0), (H,) # 输出两个: 当前小批量的输出(沿着时间步数维拼起来) & 隐藏状态H
# torch.cat(outputs, dim=0)的形状是:(时间步数量×批量大小,词表大小)定义了所有需要的函数之后,接下来我们[创建一个类来包装这些函数], 并存储从零开始实现的循环神经网络模型的参数。
In [8]:
class RNNModelScratch: #@save # 把前面定义的初始化函数+前向传播函数封装成类
"""从零开始实现的循环神经网络模型"""
def __init__(self, vocab_size, num_hiddens, device, # 把传入参数做成类变量,都存好
get_params, init_state, forward_fn): # init_state是传入“init_rnn_state”隐状态初始化函数
self.vocab_size, self.num_hiddens = vocab_size, num_hiddens
self.params = get_params(vocab_size, num_hiddens, device)
self.init_state, self.forward_fn = init_state, forward_fn # forward_fn就是上文定义的rnn()函数
# 为了后面LSTM的训练,这里做得通用一点
def __call__(self, X, state): # net是类对象,直接net(X, state)就能调用该__call__方法
# X形状就是迭代器load进来的小批量,形状:(批量大小,时间步数),是文本数据对词表的索引
X = F.one_hot(X.T, self.vocab_size).type(torch.float32) # 转置+独热编码后:(时间步数,批量,词表大小)
return self.forward_fn(X, state, self.params) # 给前向传播rnn()函数传入X,H,and初始化参数
def begin_state(self, batch_size, device): # 初始化隐状态,init_state是传入的“init_rnn_state”函数
return self.init_state(batch_size, self.num_hiddens, device)让我们[检查输出是否具有正确的形状]。 例如,隐状态的维数是否保持不变。
In [9]:
num_hiddens = 512 # 定义隐层大小
net = RNNModelScratch(len(vocab), num_hiddens, d2l.try_gpu(), get_params,
init_rnn_state, rnn) # init_state是传入的“init_rnn_state”函数,初始化0时刻前的隐状态
# 先传入一个mini batch调试,看看输出
state = net.begin_state(X.shape[0], d2l.try_gpu()) # 初始化隐状态, X.shape[0]传入batch size批量数
Y, new_state = net(X.to(d2l.try_gpu()), state) # X是上文独热编码演示的tensor形状是(2,5) = (批量数,时间步数)
Y.shape, len(new_state), new_state[0].shape # Y中的10=时间步数×批量数;28是词表大小;
# 隐层参数是1个tensor,形状是(2,512) = (批量数,隐层大小)Out[9]:
(torch.Size([10, 28]), 1, torch.Size([2, 512]))
我们可以看到输出形状是(时间步数×批量大小,词表大小), 而隐状态形状保持不变,即(批量大小,隐藏单元数)。
2.4 预测 (predict函数)
让我们[首先定义预测函数来生成prefix之后的新字符], 其中的prefix是一个用户提供的包含多个字符的字符串。 在循环遍历prefix中的开始字符时, 我们不断地将隐状态传递到下一个时间步,但是不生成任何输出。 这被称为预热(warm-up)期, 因为在此期间模型会自我更新(例如,更新隐状态), 但不会进行预测。 预热期结束后,隐状态的值通常比刚开始的初始值更适合预测, 从而预测字符并输出它们。
In [10]:
def predict_ch8(prefix, num_preds, net, vocab, device): #@save # predict_ch8在简洁实现里也可用,泛用性强
"""在prefix后面生成新字符""" # 相当于是基于给定的prefix(句子的前段),预测后面num_preds个token(补全句子)
state = net.begin_state(batch_size=1, device=device) # 因为每次只预测一句,预测模式下批量数设为1
outputs = [vocab[prefix[0]]] # prefix[0]个字符,根据token(字符)在vocab词表中拿到下标索引, 作为第0个输入
# 创建lambda一次性使用的函数,后面使用get_input()可直接调用
get_input = lambda: torch.tensor([outputs[-1]], device=device).reshape((1, 1))
# outputs[-1]是最近预测完的那个字符,作为下一个时间步的输入
for y in prefix[1:]: # 预热期 # 不断初始化(更新)隐状态,直到把prefix迭代完
_, state = net(get_input(), state) # "_,"咱不需要(不care)预热期的输出,因为已有标准答案prefix了
outputs.append(vocab[y]) # 把标准答案prefix一个一个拼到outputs(list)里
for _ in range(num_preds): # 预测num_preds步
y, state = net(get_input(), state) # y是独热编码后形状(28,)的list, H:形状(512,)的tensor
# 把预测接着拼到outputs(list)里 # y.argmax(dim=1)看最大元素在第几列,返回列的索引,方便与词表对应
outputs.append(int(y.argmax(dim=1).reshape(1)))
return ''.join([vocab.idx_to_token[i] for i in outputs]) # 根据下标索引在词表中找到token, join后返回现在我们可以测试predict_ch8函数。 我们将前缀指定为time traveller, 并基于这个前缀生成10个后续字符。 鉴于我们还没有训练网络,它会生成荒谬的预测结果。
In [11]:
predict_ch8('time traveller ', 10, net, vocab, d2l.try_gpu()) # 还没有训练模型,训练前的predict效果并不好Out[11]:
'time traveller ihcrfrfrfr'
2.5 梯度裁剪

有时梯度可能很大,从而优化算法可能无法收敛。 我们可以通过降低𝜂的学习率来解决这个问题。 但是如果我们很少得到大的梯度呢? 在这种情况下,这种做法似乎毫无道理。 一个流行的替代方案是通过将梯度𝐠投影回给定半径 (例如𝜃)的球来裁剪梯度𝐠。 如下式:
(
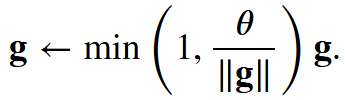
)
通过这样做,我们知道梯度范数永远不会超过𝜃, 并且更新后的梯度完全与𝐠的原始方向对齐。 它还有一个值得拥有的副作用, 即限制任何给定的小批量数据(以及其中任何给定的样本)对参数向量的影响, 这赋予了模型一定程度的稳定性。 梯度裁剪提供了一个快速修复梯度爆炸的方法, 虽然它并不能完全解决问题,但它是众多有效的技术之一。
下面我们定义一个函数来裁剪模型的梯度, 模型是从零开始实现的模型或由高级API构建的模型。 我们在此计算了所有模型参数的梯度的范数。
In [12]:
def grad_clipping(net, theta): #@save # theta: 用于限制梯度范数的阈值
"""裁剪梯度"""
if isinstance(net, nn.Module): # 如果传入的net是nn.Module类型(即标准的PyTorch神经网络模块)
params = [p for p in net.parameters() if p.requires_grad] # 那存下些requires_grad为True的可学习参数
else:
params = net.params # 如果传入的net不是nn.Module类型,假设它有一个名为params的属性来存储可训练参数
# 计算所有可训练参数的梯度的平方和的平方根,得到梯度的范数(距离之和)
norm = torch.sqrt(sum(torch.sum((p.grad ** 2)) for p in params))
if norm > theta: # 如果梯度的范数 > 阈值theta
for param in params: # 对每个可训练参数的梯度进行裁剪操作
param.grad[:] *= theta / norm # 将当前梯度乘以theta / norm来调整梯度的大小,使其范数等于theta2.6 训练 (train函数)
在训练模型之前,让我们[定义一个函数在一个迭代周期内训练模型]。 它与我们训练 :numref:sec_softmax_scratch模型的方式有三个不同之处。
- 序列数据的不同采样方法(随机采样和顺序分区)将导致隐状态初始化的差异。
- 我们在更新模型参数之前裁剪梯度。 这样的操作的目的是,即使训练过程中某个点上发生了梯度爆炸,也能保证模型不会发散。
- 我们用困惑度来评价模型。如 :numref:
subsec_perplexity所述, 这样的度量确保了不同长度的序列具有可比性。
具体来说,当使用顺序分区时, 我们只在每个迭代周期的开始位置初始化隐状态。 由于下一个小批量数据中的第𝑖个子序列样本 与当前第𝑖个子序列样本相邻, 因此当前小批量数据最后一个样本的隐状态, 将用于初始化下一个小批量数据第一个样本的隐状态。 这样,存储在隐状态中的序列的历史信息 可以在一个迭代周期内流经相邻的子序列。 然而,在任何一点隐状态的计算, 都依赖于同一迭代周期中前面所有的小批量数据, 这使得梯度计算变得复杂。 为了降低计算量,在处理任何一个小批量数据之前, 我们先分离梯度: 使用detach_()函数,使得隐状态的梯度计算总是限制在一个小批量数据的时间步内。
当使用随机抽样时,因为每个样本都是在一个随机位置抽样的, 因此需要为每个迭代周期重新初始化隐状态。 与 :numref:sec_softmax_scratch中的 train_epoch_ch3函数相同, updater是更新模型参数的常用函数。 它既可以是从头开始实现的d2l.sgd函数, 也可以是深度学习框架中内置的优化函数。
In [13]:
#@save
def train_epoch_ch8(net, train_iter, loss, updater, device, use_random_iter): # use_random_iter是否随机采样
"""训练网络一个迭代周期(定义见第8章)""" # 1个epoch
state, timer = None, d2l.Timer()
metric = d2l.Accumulator(2) # 存下训练损失之和,词元数量
# ※※ 与mlp主要的不同在这里 ※※
for X, Y in train_iter: # 每个mini batch
if state is None or use_random_iter: # 如果一开始没有隐变量,or 启用随机采样iterator迭代器
# 在第一次迭代或使用随机抽样时初始化state(隐状态H),隐状态H不连续,得初始化
state = net.begin_state(batch_size=X.shape[0], device=device) # 使用begin_state函数
else: # 如果使用顺序分区(采样)-(语言模型小节有讲),每个批量首尾相连,隐状态H是连续的,不用做初始化
if isinstance(net, nn.Module) and not isinstance(state, tuple):
# state对于nn.GRU是个张量
state.detach_() # detach_()主要是反向传播更新梯度时,由于H是连续的,1个epoch初始化一次H
# 每个epoch中H的计算图会是一个特别长的序列(一大串乘法),这些之前批量的计算图用不上
# 把当前batch计算之前的隐层变量的计算图(一大串乘法)全去掉(detach掉),反向传播只算当前batch的
else:
# state对于nn.LSTM或对于我们从零开始实现的模型是个张量
for s in state:
s.detach_()
# ※※※ 形状一定要搞清楚!!!※※※
# X是迭代器load进来的小批量,前面的class类中已给X做转置+独热编码后的形状:(时间步数,批量大小,词表大小)
# 但Y的形状还是(批量大小,时间步数),对应开头的(32,35),reshape(-1)按照行(转置后行是时间步),拉成1维向量
y = Y.T.reshape(-1) # y的形状很重要,不然后面算loss不好理解:y的形状(时间步数×批量大小,) = (1120,)
X, y = X.to(device), y.to(device) # 放到GPU上
y_hat, state = net(X, state) # 每个mini batch做forward前向传播函数,请回顾rnn()
# 在forward函数(就是rnn())中,y_hat通过拼接后形状是:(时间步数量×批量大小,词表大小)
# y_hat是浮点数,y.long()将y也转成浮点数,y的形状:(时间步数×批量大小,)
l = loss(y_hat, y.long()).mean() # 每个batch算loss; 用到了广播机制
# 和mlp基本一样,不同在多了个grad_clipping()多了个梯度剪裁
if isinstance(updater, torch.optim.Optimizer):
# 如果updater是标准的优化器对象,首先将梯度清零
updater.zero_grad()
l.backward() # 每个mini batch
grad_clipping(net, 1) # 咱这里剪裁比较狠,梯度总长度超过 1 就进行梯度剪裁
updater.step()
else:
l.backward()
grad_clipping(net, 1)
# 因为已经调用了mean函数
updater(batch_size=1) # 从零实现时,默认batch_size=1,后面train_ch8()中有定义
# 每个mini batch: 用y.numel()计数样本数;用“l(损失) * y.numel(样本数)”算一个batch的总损失
metric.add(l * y.numel(), y.numel()) # 每个batch,metric的对应元素都会累加,形状是(2,)
# 算困惑度(Perplexity):对每个token的平均损失值取指数exp();
return math.exp(metric[0] / metric[1]), metric[1] / timer.stop() # timer.stop()计时器,算每秒多少token[循环神经网络模型的训练函数既支持从零开始实现, 也可以使用高级API来实现。]
In [14]:
#@save # 这里定义一次,后面GRU,LSTM都能用
def train_ch8(net, train_iter, vocab, lr, num_epochs, device,
use_random_iter=False):
"""训练模型(定义见第8章)"""
loss = nn.CrossEntropyLoss() # 虽说是语言模型,但用了独热编码后,还是多分类,用交叉熵损失
animator = d2l.Animator(xlabel='epoch', ylabel='perplexity',
legend=['train'], xlim=[10, num_epochs]) # 画图,可以忽略
# 初始化
if isinstance(net, nn.Module):
updater = torch.optim.SGD(net.parameters(), lr) # updater是标准的pytorch优化器对象(简洁实现)
else:
# 在train_epoch_ch8()函数中,使用updater(batch_size=1)来调用
updater = lambda batch_size: d2l.sgd(net.params, lr, batch_size) # 从零实现模式
# 定义预测函数,lambda是临沭函数,调用时传入predict(prefix)
predict = lambda prefix: predict_ch8(prefix, 50, net, vocab, device) # 给标准答案prefix,预测后50个token
# 训练和预测
for epoch in range(num_epochs):
ppl, speed = train_epoch_ch8( # ppl:困惑度; speed:每秒训练多少token
net, train_iter, loss, updater, device, use_random_iter)
if (epoch + 1) % 10 == 0: # 若epoch被10整除
print(predict('time traveller')) # 每10个epoch执行一下打印和预测;会拖累运算速度,但检查点有必要
animator.add(epoch + 1, [ppl]) # 向图中添加数据点,“epoch + 1”是横坐标,[ppl]是纵坐标
print(f'困惑度 {ppl:.1f}, {speed:.1f} 词元/秒 {str(device)}')
print(predict('time traveller')) # 调用预测函数
print(predict('traveller'))[现在,我们训练循环神经网络模型。] 因为我们在数据集中只使用了10000个词元, 所以模型需要更多的迭代周期来更好地收敛。
In [15]:
num_epochs, lr = 500, 1
train_ch8(net, train_iter, vocab, lr, num_epochs, d2l.try_gpu()) # net默认是顺序分区(采样)
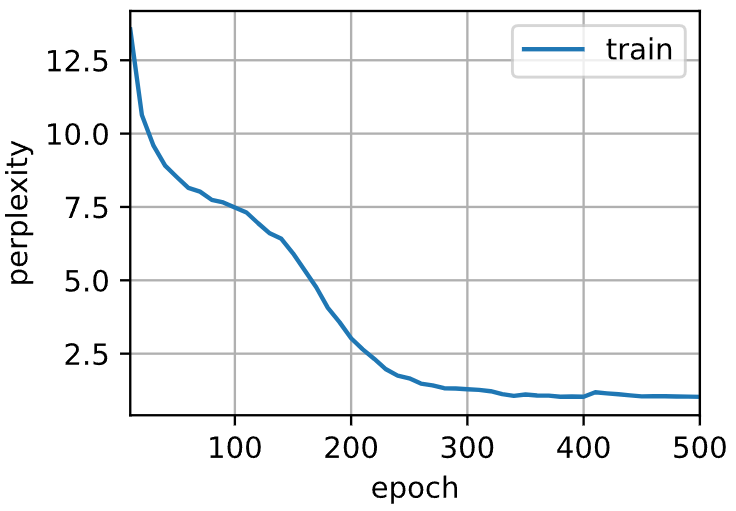
# 看结果,困惑度是1,基本上完美记住了整本书,毕竟扫了500遍
# 语言模型的特点是远看(词的拼写)还可以,细看发现内容(逻辑)不太行困惑度 1.0, 78577.2 词元/秒 cuda:0 time travelleryou can show black is white by argument said filby travelleryou can show black is white by argument said filby
[最后,让我们检查一下使用随机抽样方法的结果。]
In [16]:
net = RNNModelScratch(len(vocab), num_hiddens, d2l.try_gpu(), get_params,
init_rnn_state, rnn) # 启用随机抽样,每个batch不连续
train_ch8(net, train_iter, vocab, lr, num_epochs, d2l.try_gpu(),
use_random_iter=True)
# 训练的数据集的文本还是太小啦,记住了很多东西,但越往后问题越大(误差积累)困惑度 1.6, 84514.7 词元/秒 cuda:0 time travellerit s against reason said filbywhat wh shond ta mom travellerit s against reason said filbywhat wh shond ta mom
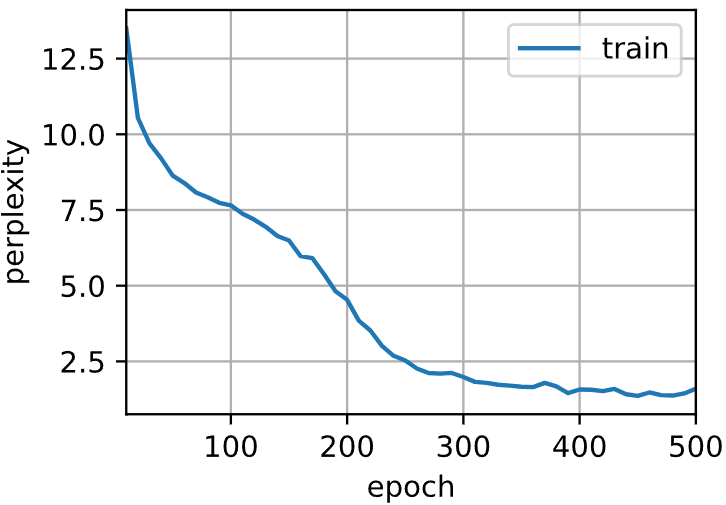
从零开始实现上述循环神经网络模型, 虽然有指导意义,但是并不方便。 在下一节中,我们将学习如何改进循环神经网络模型。 例如,如何使其实现地更容易,且运行速度更快。
2.7 小结
- 我们可以训练一个基于循环神经网络的字符级语言模型,根据用户提供的文本的前缀生成后续文本。
- 一个简单的循环神经网络语言模型包括输入编码、循环神经网络模型和输出生成。
- 循环神经网络模型在训练以前需要初始化状态,不过随机抽样和顺序划分使用初始化方法不同。
- 当使用顺序划分时,我们需要分离梯度以减少计算量。
- 在进行任何预测之前,模型通过预热期进行自我更新(例如,获得比初始值更好的隐状态)。
- 梯度裁剪可以防止梯度爆炸,但不能应对梯度消失。
3. RNN 的简洁实现
虽然 :numref:sec_rnn_scratch 对了解循环神经网络的实现方式具有指导意义,但并不方便。 本节将展示如何使用深度学习框架的高级API提供的函数更有效地实现相同的语言模型。 我们仍然从读取时光机器数据集开始。
In [1]:
import torch
from torch import nn
from torch.nn import functional as F
from d2l import torch as d2l
batch_size, num_steps = 32, 35
train_iter, vocab = d2l.load_data_time_machine(batch_size, num_steps)3.1 定义模型
高级API提供了循环神经网络的实现。 我们构造一个具有256个隐藏单元的单隐藏层的循环神经网络层rnn_layer。 事实上,我们还没有讨论多层循环神经网络的意义(这将在 :numref:sec_deep_rnn中介绍)。 现在仅需要将多层理解为一层循环神经网络的输出被用作下一层循环神经网络的输入就足够了。
In [2]:
num_hiddens = 512 # 原文是256,改为512是为了和“从零实现”的隐层数相同,控制变量方便对比
rnn_layer = nn.RNN(len(vocab), num_hiddens) # torch有RNN的类,直接传入(输如输出维度,隐层数)我们(使用张量来初始化隐状态),它的形状是(隐藏层数,批量大小,隐藏单元数)。
In [3]:
state = torch.zeros((1, batch_size, num_hiddens)) # 手动初始化一下隐藏状态
state.shape # 加了这个“1”并做成tuple来存state还是为了LSTM,LSTM会变为“2”有两个隐变量Out[3]:
torch.Size([1, 32, 512])
[通过一个隐状态和一个输入,我们就可以用更新后的隐状态计算输出。] 需要强调的是,rnn_layer的“输出”(Y)不涉及输出层的计算: 它是指每个时间步的隐状态,这些隐状态Y可以用作后续输出层的输入。
In [4]:
X = torch.rand(size=(num_steps, batch_size, len(vocab)))
Y, state_new = rnn_layer(X, state) # Y的形状(时间步数,批量大小,隐藏层数),Y不是输出层输出,而是隐状态H
Y.shape, state_new.shape # state_new是隐层参数W_xh; Y的前两维并没有像“从零实现”那样用nn.cat拼接起来Out[4]:
(torch.Size([35, 32, 512]), torch.Size([1, 32, 512]))
与 :numref:sec_rnn_scratch类似, [我们为一个完整的循环神经网络模型定义了一个RNNModel类]。 注意,rnn_layer只包含隐藏的循环层,我们还需要创建一个单独的输出层。
In [5]:
#@save
class RNNModel(nn.Module): # 与“从零实现”的模型定义不同:没有显式的output输出函数,得用线性层来隐式定义
"""循环神经网络模型""" # 因此得构造nn.Linear作为输出层
def __init__(self, rnn_layer, vocab_size, **kwargs):
super(RNNModel, self).__init__(**kwargs) # super类继承,调用父类nn.Module的__init__方法初始化**kwargs
self.rnn = rnn_layer
self.vocab_size = vocab_size
self.num_hiddens = self.rnn.hidden_size
# 如果RNN是双向的(之后将介绍),num_directions应该是2,否则应该是1
if not self.rnn.bidirectional:
self.num_directions = 1
self.linear = nn.Linear(self.num_hiddens, self.vocab_size) # 输入:隐藏层数;输出:词表大小
else: # Linear层作为输出层,其形状:(隐藏层数,词表大小)
self.num_directions = 2 # 如果是双向RNN,后面将介绍
self.linear = nn.Linear(self.num_hiddens * 2, self.vocab_size)
def forward(self, inputs, state): # 和从零实现类似 # inputs的形状:(批量大小,时间步数量)
X = F.one_hot(inputs.T.long(), self.vocab_size) # 转置+独热编码后:(时间步数量,批量大小,词表大小)
X = X.to(torch.float32)
Y, state = self.rnn(X, state)
# Y是隐藏表示:形状(时间步数量,批量大小,隐藏层数)
# state是隐层可学习参数,形状:(1, 32, 512)
# Y.shape[-1] = 隐藏层数,shape中的“-1”指最后一维;而reshape中的“-1”会自动基于其它维来算出该维
# 全连接层首先将Y的形状改为(时间步数*批量大小,隐藏单元数),作为传入
# 它的输出output的形状: (时间步数*批量大小,词表大小)。
output = self.linear(Y.reshape((-1, Y.shape[-1])))
return output, state
def begin_state(self, device, batch_size=1):
if not isinstance(self.rnn, nn.LSTM):
# nn.GRU(门循环)以张量作为隐状态
return torch.zeros((self.num_directions * self.rnn.num_layers,
batch_size, self.num_hiddens),
device=device)
else:
# nn.LSTM以元组作为隐状态
return (torch.zeros((
self.num_directions * self.rnn.num_layers,
batch_size, self.num_hiddens), device=device),
torch.zeros((
self.num_directions * self.rnn.num_layers,
batch_size, self.num_hiddens), device=device))3.2 训练与预测
在训练模型之前,让我们[基于一个具有随机权重的模型进行预测]。
In [6]:
device = d2l.try_gpu()
net = RNNModel(rnn_layer, vocab_size=len(vocab))
net = net.to(device)
# predict_ch8预测函数在“RNN从零实现”里有定义,如此泛用说明从零实现的net输出和这里一样
d2l.predict_ch8('time traveller', 10, net, vocab, device) # 模型知识随机初始化,还没训练,看看预测效果Out[6]:
'time travellerhjrrhjrrhj'
很明显,这种模型根本不能输出好的结果。 接下来,我们使用 :numref:sec_rnn_scratch中 定义的超参数调用train_ch8,并且[使用高级API训练模型]。
In [7]:
num_epochs, lr = 500, 1
d2l.train_ch8(net, train_iter, vocab, lr, num_epochs, device)
# 看速度,用框架比从零实现快3-4倍,主要原因在上文(搜:cat((W_xh, W_hh))有介绍,拼成大矩阵乘法比多个小矩阵开销小perplexity 1.0, 279945.2 tokens/sec on cuda:0 time travelleryou can show black is white by argument said filby travelleryou can show black is white by argument said filby
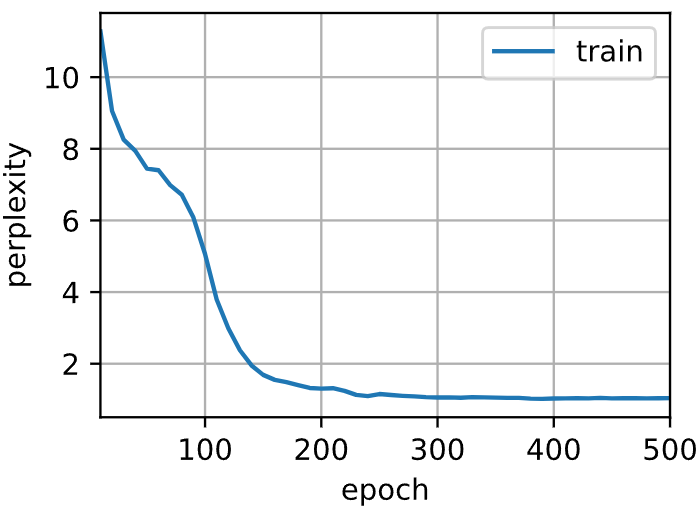
与上一节相比,由于深度学习框架的高级API对代码进行了更多的优化, 该模型在较短的时间内达到了较低的困惑度。
3.3 小结
- 深度学习框架的高级API提供了循环神经网络层的实现。
- 高级API的循环神经网络层返回一个输出和一个更新后的隐状态,我们还需要计算整个模型的输出层。
- 相比从零开始实现的循环神经网络,使用高级API实现可以加速训练。
更多推荐
 已为社区贡献8条内容
已为社区贡献8条内容











所有评论(0)