相机标定是计算机视觉领域一个久远而非常重要的问题；也是面试过程中经常出现的问题。相机标定涉及的知识面很广，成像几何、镜头畸变、单应矩阵、非线性优化等。相机标定有自标定（找图像中特征点）、标定板标定（特征点易求，稳定性好），一般采用标定板标定。相机标定按照相机是否静止，可分为静态相机标定（标定板动，相机静止），动态相机标定（标定板静止，相机运动）。动态相机标定有点slam、3维重建的感觉了吧，有些人可能觉得相机标定没啥意思，先看一张位姿估计的图片。没有标定就没有精确的位姿信息，so，相机标定很重要。

计算机视觉基础——相机标定https://www.zhihu.com/video/1168549411294019584

1物理模型

1.1 浅谈标定

首先谈谈相机为什么需要标定？任何理论物理模型都是在特定假设上对真实事物的近似，然而在实际应用中存在误差，普通相机的成像模型也不例外（透视投影）。实际中，普通相机成像误差的主要来源有两部分，第一是sensor制造产生的误差，比如sensor成像单元不是正方形，sensor歪斜；第二是镜头制造和安装产生的误差，镜头一般存在非线性的径向畸变；镜头与相机sensor安装不平行，还会产生切向畸变。

1.2透视投影模型

普通相机的成像模型一采用小孔成像，初中的物理知识告诉我们，没错，就是那个蜡烛成像实验，物体经小孔后，在成像平面成倒立的像。为了更好的进行理论阐述，一般默认采用虚拟成像平面（virtual image plane）进行分析。虽没有明文规定，但大家（不，是大佬）都是这么做的。Matlab官方有张很形象的图片。

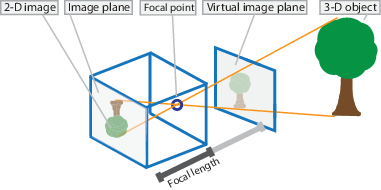
将小孔成像模型简化成几何表达的形式，图2来自多目几何第二版。

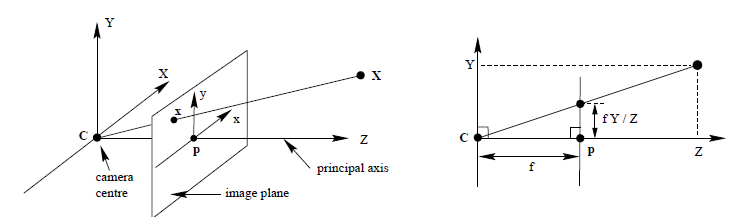
在理想情况下，根据简单的相似三角形几何知识，可以推出3D目标点在相机坐标系下的坐标与图像像素坐标之间的关系， 如公式1-1：

f是焦距，X、Y、Z是3D点在相机坐标系坐标，u，v是图像坐标；

上述公式写成齐次坐标为：

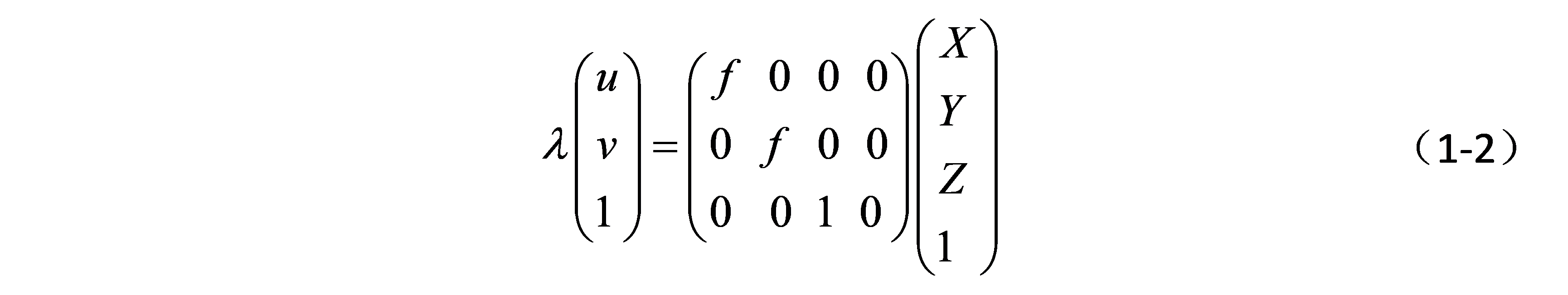
λ为尺度因子，同一条投影线上的点都满足上述关系，只是λ不同而已；在不换sensor情况下，想增大物体分辨率，其实只要把相机靠近一点就行。

1.3主点偏移

主点是光轴和相机成像平面的交点，1.2节考虑的是理想成像情况，图像坐标系和相机坐标系原点重合，因此不存在坐标系偏移。但是在实际情况中，图像坐标系往往在图片的左上角，光轴过图像中心，因此图像坐标系和相机坐标系不重合。两个坐标系之间存在一个平移运动（如图）。

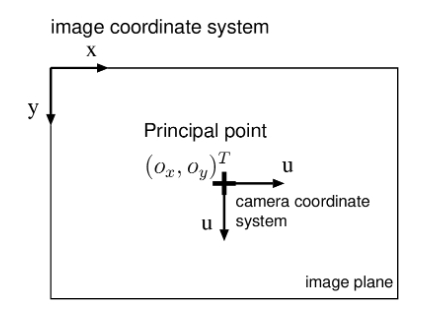
考虑主点偏移后，图像坐标和3D在相机坐标系坐标的关系为：

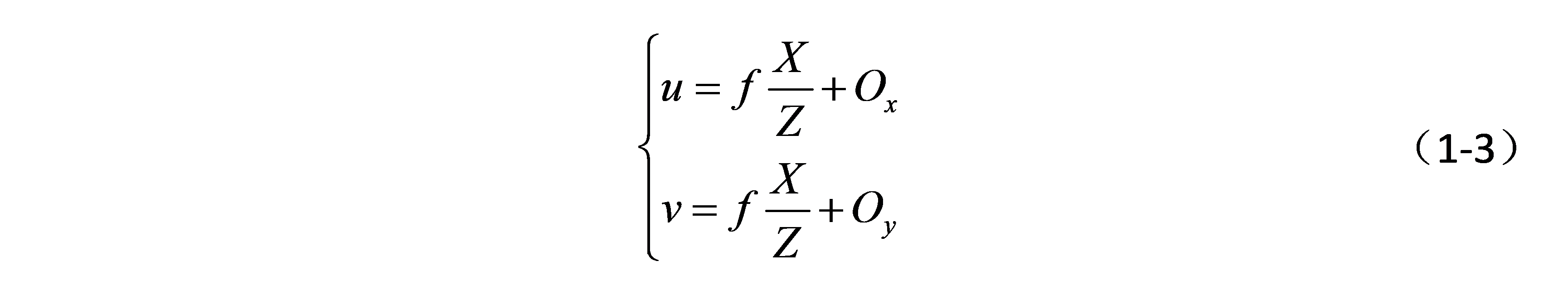
主点偏移后，透视投影模型的的齐次坐标表达为：

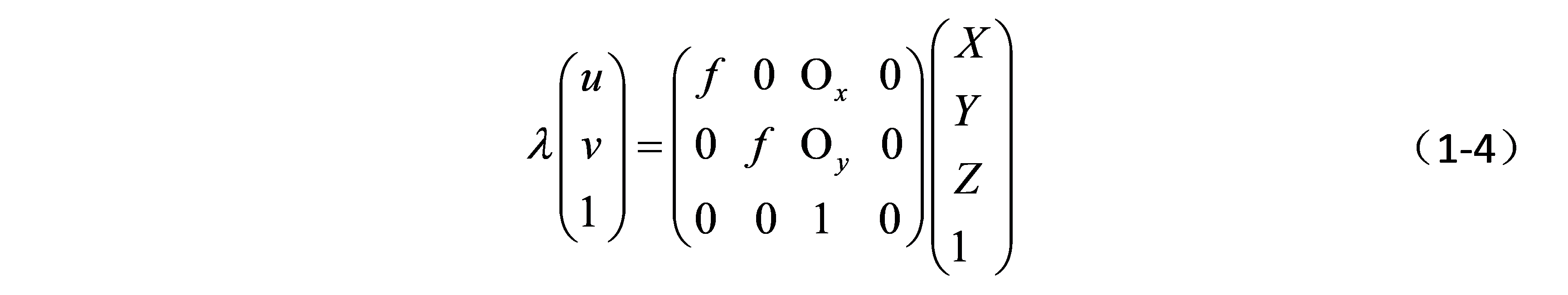
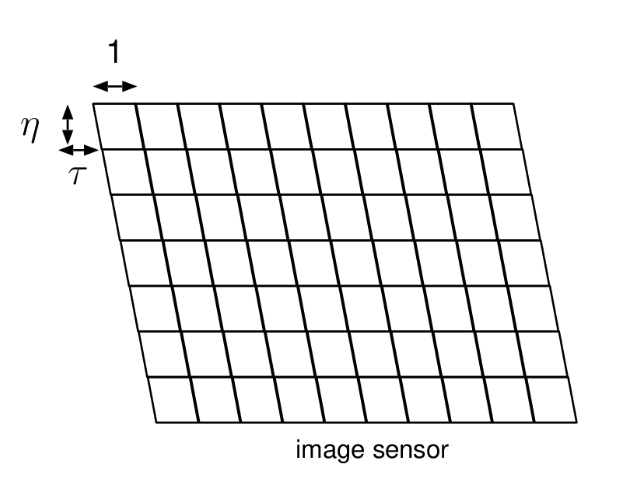
1.4 图像传感器特性

图像传感器像原尺寸在制造过程可能不是正方形，同时可能存在歪斜（skewed），因此需要考虑这些影响因素，传感器歪斜和不是正方形主要对相机x和y方向的焦距产生影响，数学表达见公式（1-5）。

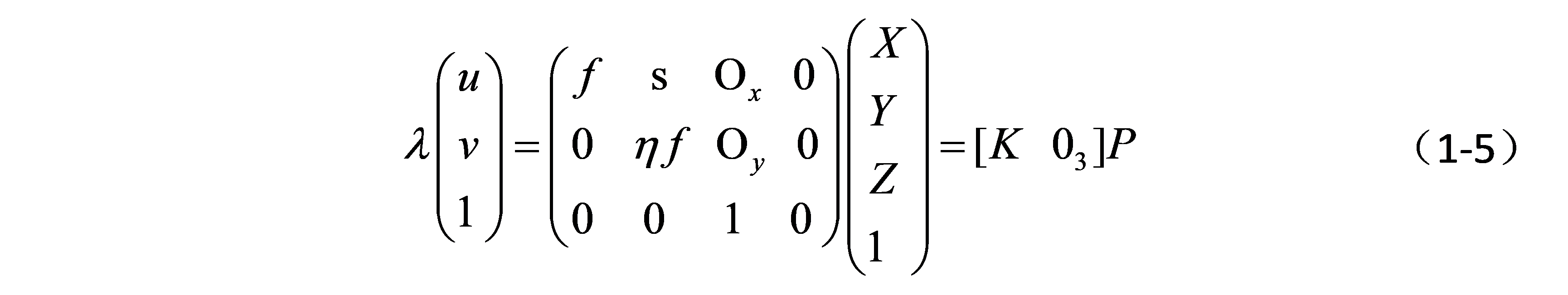
在不考虑畸变的情况下，考虑主点偏移、图像传感器的特性，3D目标点成像数学模型用公式（1-5）可完全表达。这就是相机内部参数对成像的影响，因此K称为内参矩阵，相机内参标定主要是标定相机的焦距、主点、歪斜等内部参数。

1.4镜头畸变对成像的影响

小孔成像模型虽然充分考虑了相机内部参数对成像的影响，但没有考虑成像系统另一个重要的部分，镜头。镜头常用的有普通镜头、广角镜头、鱼眼镜头等，在无人驾驶和视觉slam领域，鱼眼镜头和广角镜头用的很多，主要是视角很大，可以观测到更多的信息。任何镜头都存在不同程度的畸变，不同类型的镜头用到的畸变模型也不相同。根据镜头制造和成像的物理特性，普通镜头主要考虑径向畸变和切向畸变，且畸变模型都可以用多项式来近似。而对于大广角、鱼眼镜头，普通镜头的物理模型不能适用了。

鱼眼镜头畸变校正请参考：

https://www.mathworks.com/help/vision/ug/fisheye-calibration-basics.html

1.4.1径向畸变

透过镜头边缘的光线很容易产生径向畸变，光线离镜头中心越远，畸变越大。

从图像可以看出，径向畸变以某一个中心往外延伸，且越往外，畸变越大；显然畸变与距离成一种非线性的变换关系，参考众多文献，可以用多项式来近似。

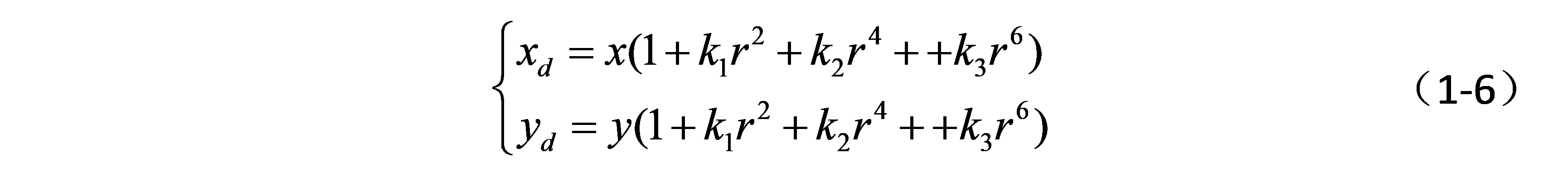
x,y是归一化的图像坐标，即坐标原点已经移动到主点，并且像素坐标除以焦距。K1,k2,k3是径向畸变系数，r2=x2+y2（2表示2次方）。

1.4.2切向畸变

切向畸变主要发生在相机sensor和镜头不平行的情况下；因为有夹角，所以光透过镜头传到图像传感器上时，成像位置发生了变化。

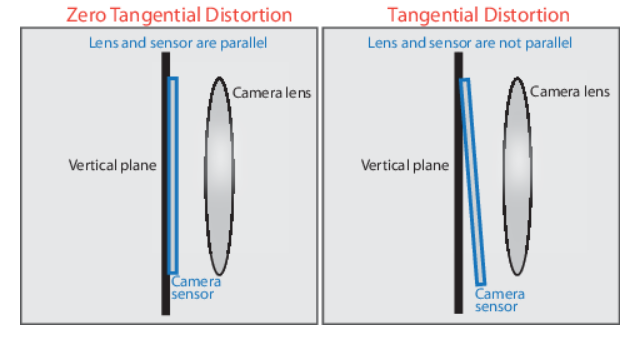
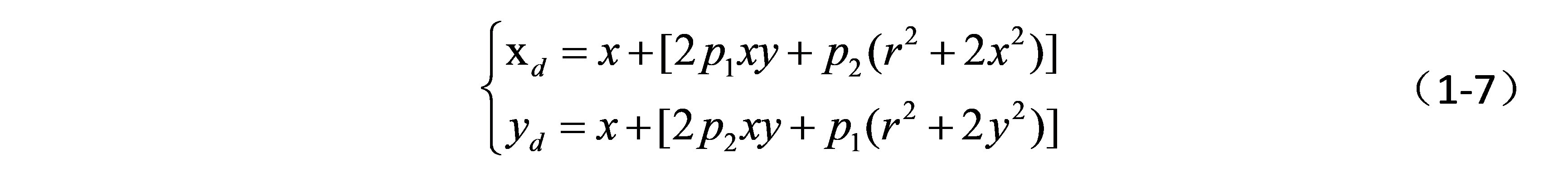
x,y是归一化的图像坐标，即坐标原点已经移动到主点，并且像素坐标除以焦距。p1、p2是径向畸变系数，r2=x2+y2。

1.5相机外参

上述讨论的范畴全是在相机坐标下发生的事情，然而实际情况是，相机往往装在机械臂末端，移动小车前方，车辆四周，当我们需要知道成像平面内的物体在机器人或者车辆坐标系下的位置时，需要进行一个坐标转换，称为外参（Extrinsic parameters），它与相机制造、镜头畸变没有任何关系，只与相机在世界坐标系内的安装位置和角度有关。从纯数学的角度来说，刚体运动和坐标变换总是可以分解为一个旋转运动和一个平移运动。

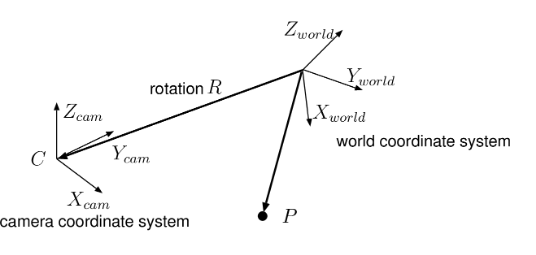
因此世界坐标系下的点P与图像坐标的关系可以表达为：

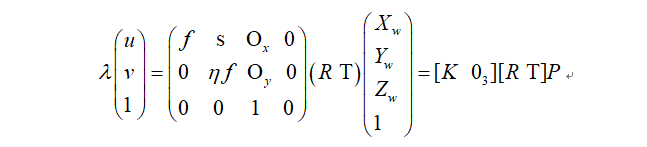
相机标定就是标定内参和外参，通过一种理论数学模型和优化的手段来近似实际的物理成像关系。

2 模型求解

模型求解数学公式繁多，需要有些线性代数基础，对公式无感者，直接跳过本节，这一节和上一节的公式符号略有出入，保持原paper符号。

2.1 内参和单应矩阵关系

搞清楚了理论模型，接下来就是求解未知的内参和外参了。推荐张正友祖师爷98年的paper，因为内参的初始估计有闭环解，不需要凭感觉瞎估，这是非常非常爽的事情。空间中的3D点投影到图像上的关系为：

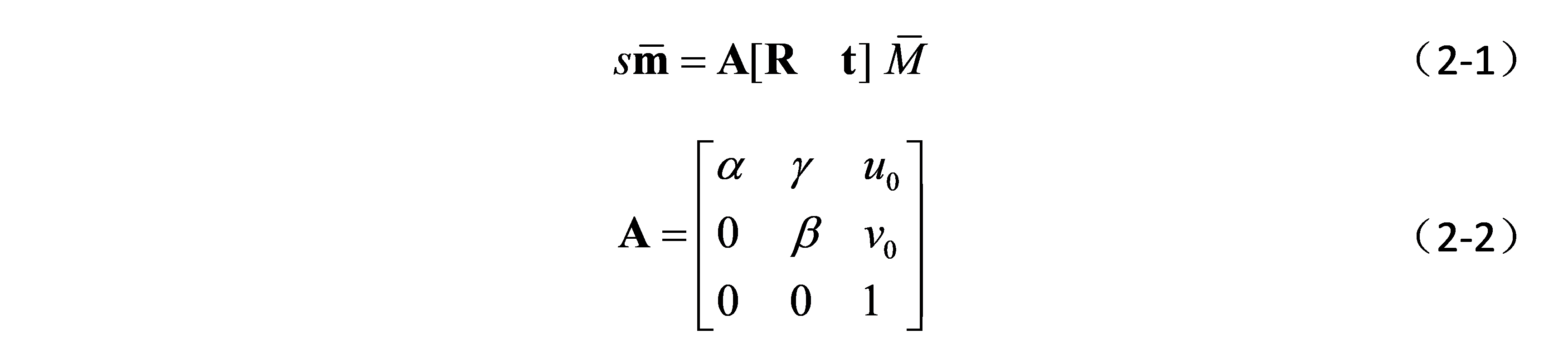
一般我们都会用标定板来标定，所有的特征点都在一个平面上，不失一般性，可以假设这个平面的空间Z坐标为0，将外参R矩阵写成列向量的形式为：

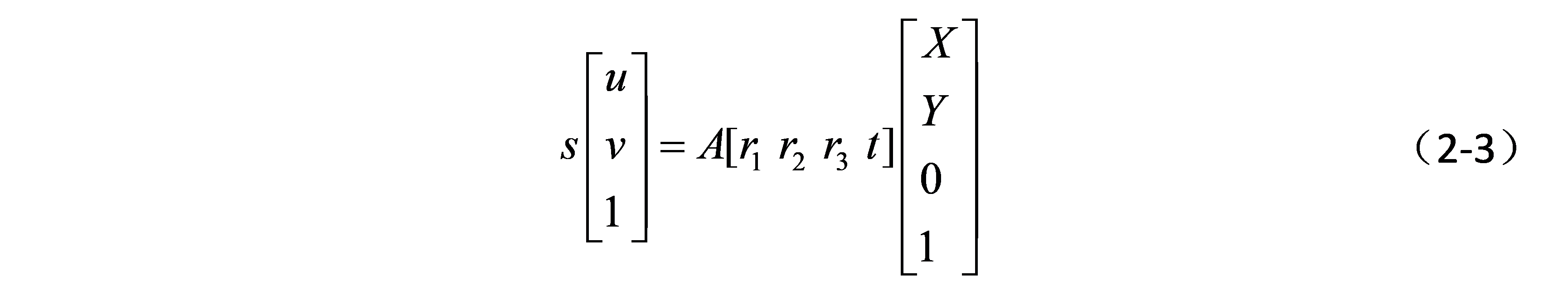
因为Z=0，可以去掉r3列向量，化简为：

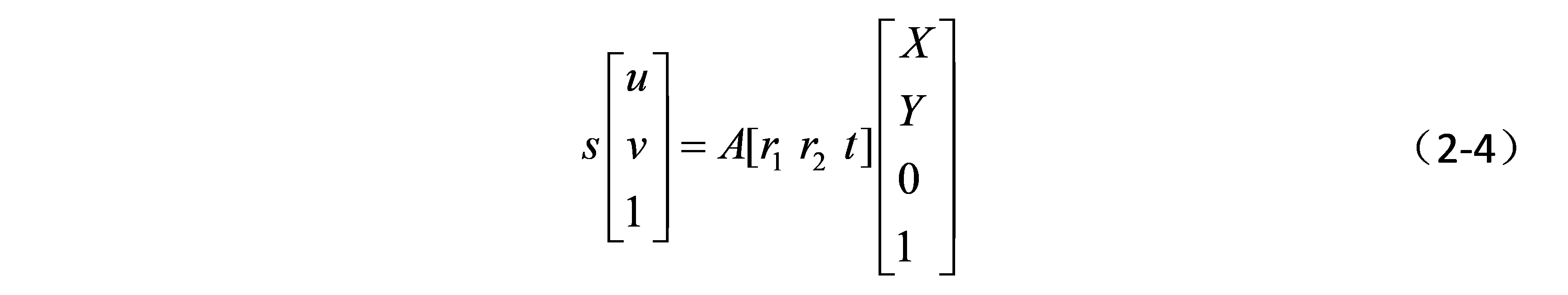
因此，空间3D点和图像坐标之间通过一个单应矩阵H（homography）联系在一起，单应矩阵如下，

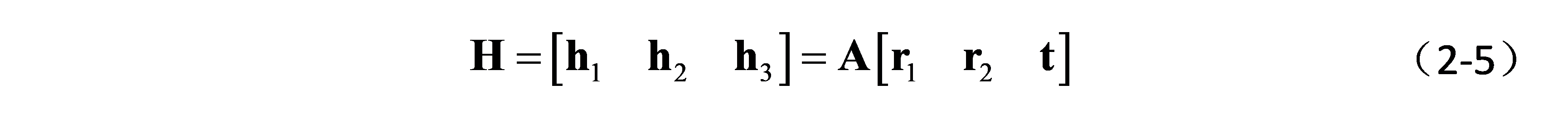
这个单应矩阵H可以根据棋盘格角点的实际坐标和图像对应坐标求出，参考多目几何直接线性化方法（DLT），每一张图像都会形成一个单应矩阵。因此，单应矩阵可以作为一个前期求出的已知量。

变换公式（2-5）得：

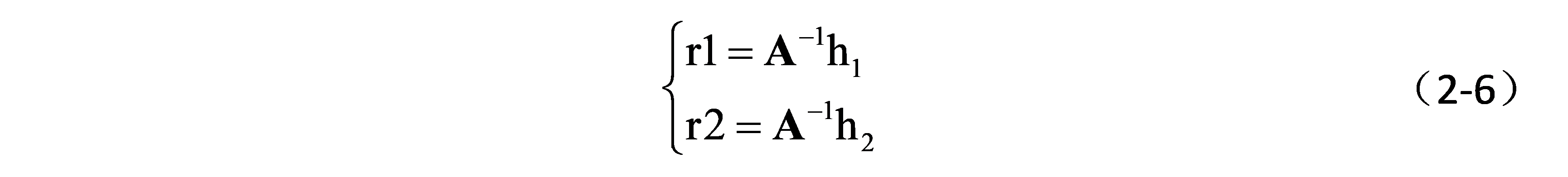
由于向量r1与r2正交且长度都为1，因此可以得出以下关系：

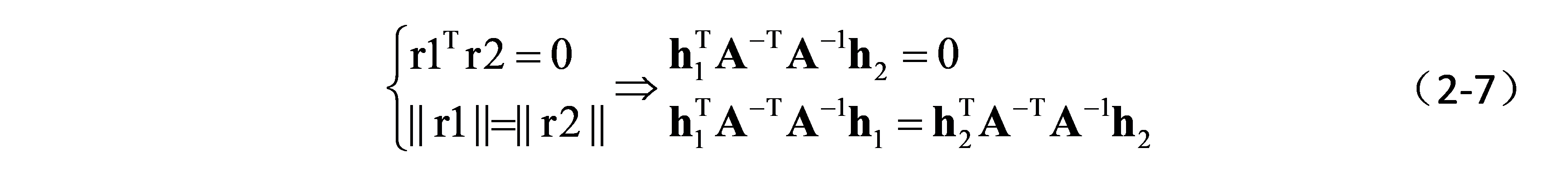
2.2 闭环求解（Closed-form solution）

闭环解就是说的完全可以靠理论，数学推导可以求出的，不需要进行数值计算，也是非常爽的，程序按照公式写即可。数学中一个伟大的术语是不妨设，太魔幻了。

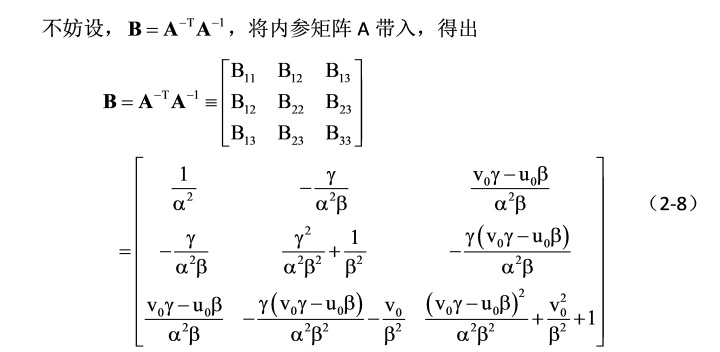
终于看到胜利的曙光了，这公式见得太多了。V是只由单应矩阵决定的已知量，求解上述线性方程，就可以得到向量b，矩阵B。向量b包含6个未知量，V是2n x 6矩阵，n代表单应矩阵个数（或者图像张数），所以至少需要采集三张不同位置或者角度的图像，才能求解上述方程。实际中，为了降低误差，会采集15-20张图像。

关于Ax = 0形式的求解，证明可以参考文章，拿走不谢。

https://www.cnblogs.com/BellaVita/p/10003528.html。

既然B矩阵已经求出，那后面的事就是手到擒来了，按照公式编辑程序即可。相机内参A和B矩阵的关系（根据公式2-8），推出如下

2.3 优化

可能有的人认为到这就完了，内外参数都求出来了，别忘了还有个镜头畸变系数没处理。那这怎么计算呢，就假设一开始没有畸变，畸变系数全是0呗，没有畸变的时候，内外参就是2.2节求出的闭环解。这不就是给你初始值，然后xxxx，没错，就是优化。

关于优化，需要目标函数、约束条件、优化方法、优化变量。在相机标定中，目标函数采用最小化重投影误差，即将空间坐标按照估计的投影方程投影到图像上，得到像素估计值，使该值与实际观测值（例：棋盘格角点坐标）之间的误差最小。这感觉是不是很熟悉，做视觉slam的同学，想想BA，嘿嘿。

目标函数：

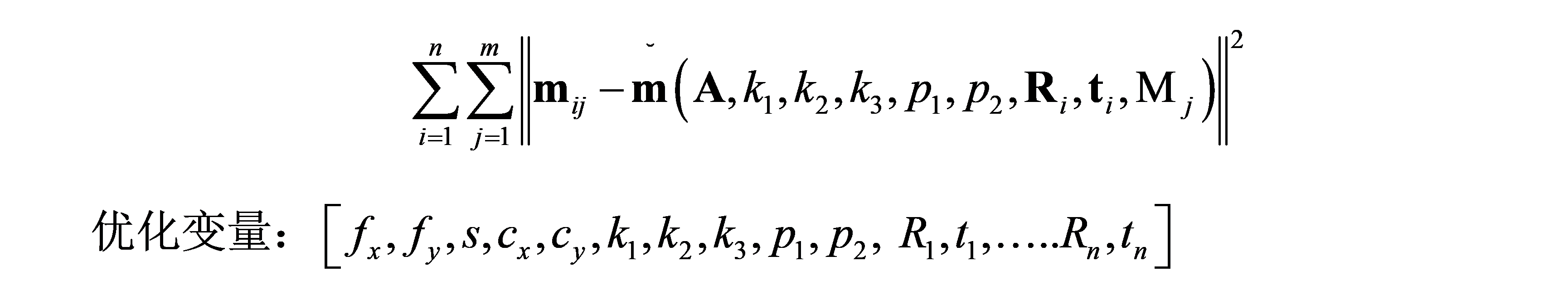
优化变量初始值：闭环解，畸变系数初始为0

优化方法：LM

这一节涉及的数学知识，更加多，也更加难以理解。想需要深入的同学，推荐好的资料，拿走不谢，请自行google。

关于链式微分：高等数学，任何教材

关于非线性优化：DTU：Methods for non-linear least squares problems，建议看整套的文档，从最速下降、牛顿法开始，然后看LM。

关于李代数和矩阵求导：Time Derivative of Rotation Matrices

关于相机标定非线性优化opencv源代码：calibration.cpp

3结果

1、Matlab有现成的标定界面，很酷

2、opencv有很好的棋盘格检测效果，想要提高精度的，请参考角点优化、亚像素精度方面的文章。

3、视频

计算机视觉基础——相机标定https://www.zhihu.com/video/1168570773014355968

from: 北辰

斯坦德机器人