接上一篇 基于GMM-HMM的语音识别系统（1）

二. 三音素GMM-HMM模型

使用三音素建模之后，引入了新的问题：

1. N个音素，则共有
   个三音素，若N=100，则建模单元又太多了，每个音素有三个状态，每个状态对应的GMM参数，参数就太多了。
2. 数据稀疏问题，有的三音素数据量很少
3. unseen data问题。有的三音素在训练数据没有出现，如K-K+K，但识别时却有可能出现，这时如何描述未被训练的三音素及其概率

所以通常我们会根据数据特征对triphone的状态进行绑定，常见的状态绑定方法有数据驱动聚类(Data-Driven Clustering)和决策树聚类(Tree-Based Clustering)，现在基本上是使用决策树聚类的方式。

2.1 三音素建模：使用决策树

三音素GMM-HMM模型是在单音素GMM-HMM模型的基础上训练的，流程如下图所示。为什么要先进行单音素GMM-HMM训练？因为要通过在单音素GMM-HMM模型上viterbi算法得到与输入

（1）构建什么样子的决策树？可以解决哪些问题？

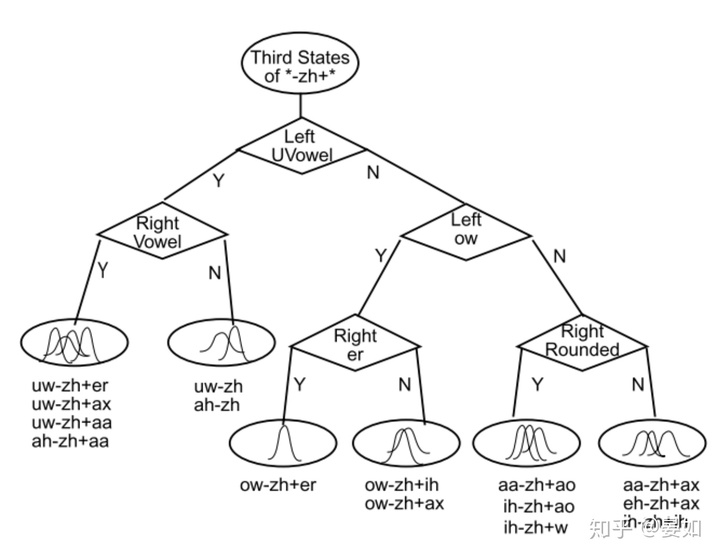
• 将要构建的决策树，是一棵二叉树，该二叉树有菱形和椭圆形的节点。
• 从图上来看，除了根节点（third states of *-zh+*）和叶子节点，其他节点上都有一个问题，由菱形表示的，比如根节点出来的第一个菱形节点，Left UVowel问当前三音素的左边的音素是不是一个UVowel，Right Vowel是问当前三音素的右边的音素是不是一个元音音素。每个三音素对于该问题都会有一个Yes或No的的答案，那么对所有的三音素来讲，该问题会把所有三音素分成Yes集合和No集合。【有的系统在实现的时候，和这个图不一样，但是构建二叉树的原理和目标是一样的】。
• 从根节点经过一些列的问题，相近（相似度高）的（绑定）三音素到达同一个叶子节点。
• 决策树建立的基本单元是状态，对每个三音素的每个state建立一颗属于他们自己的决策树。

构建的决策树是否解决了“使用三音素建模之后，引入了新的三个问题”？即建模单元数过多、数据稀疏、unseen data的问题。

（2）问题集怎么得到？怎么设置问题和提问顺序可以使得聚类过程又快又好？

问题集的生成分为两种，一种是语言学家定义，另一种是自动生成，如何自动生成，还在学习中，以后添加相关知识。

第二个问题：怎么设置问题和提问顺序可以使得聚类过程又快又好？在下文中决策树生成过程来回答。

（3）将构建决策树这个问题形式化：

• 输入：a）单音素系统，并且通过viterbi算法，得到单音素各个状态所有对应的观察序列（即输入特征序列）；b）问题集
• 目标：将单音素扩展为三音素，对每个三音素的每个状态（有三个状态）建立一颗属于它们自己的决策树，从而达到状态绑定的目的。
• 输出：带决策树的三音素GMM-HMM系统

（4）构建决策树的步骤：

step 1: 通过上下文扩展，从单音素状态得到三音素状态

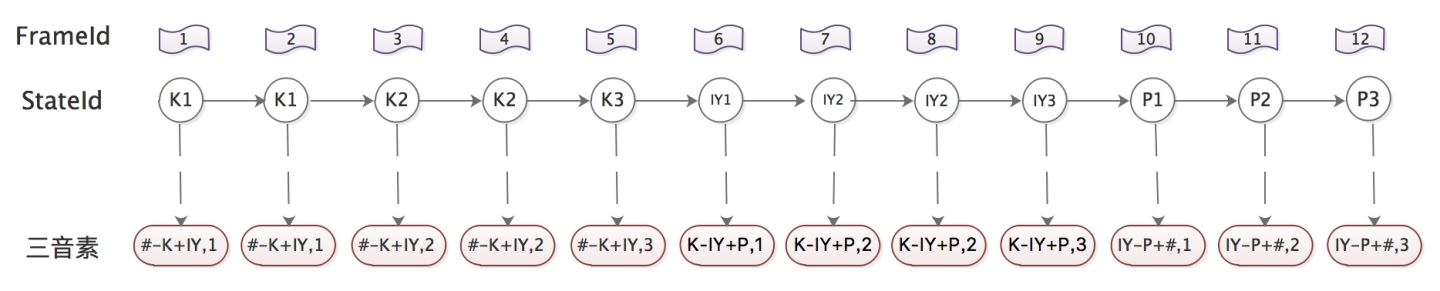
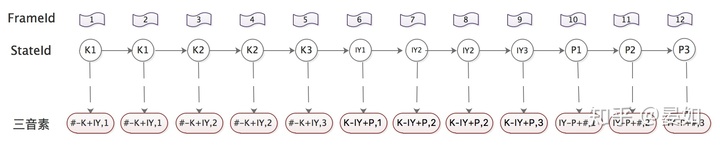
以keep /K IY P/为例，现在有12帧观察序列，在单音素系统中通过viterbi算法得到了最佳状态序列，然后通过上下文扩展，得到三音素状态与观察序列的对应关系(逗号后面的数字，1、2、3表示这是三音素的第几个状态) 。这个过程就是单音素对齐转为三音素对齐。

step 2: 通过问题集，从根节点开始分裂，构建决策树

如果不考虑决策树，只考虑GMM-HMM系统的训练过程，我们就会使用第1、2帧的输入特征数据来估计 三音素#-K+IY 第一个状态的观察概率gmm，第3、4帧的输入数据来估计三音素 #-K+IY 第二个状态的观察概率gmm……，那这样就与三音素的过程无异了，也并没有提升精细化建模的能力。通过决策树，将输入数据对应到更加精细化的gmm模型。

根节点就是三音素的状态节点，比如#-K+IY,1 和#-K+IY,2。比如图2中，对于*-zh+*第三个状态，我们的初始条件类似决策树这张图中的根节点"Third states of *-zh+*"，下面所面临的问题是如何一步一步分裂该节点，而分裂该节点，其实就是如何从问题集中选择问题，能够使相近的三音素分类到相同的节点上。

还是假设本文中所有三音素状态的观察概率服从单高斯分布（多维特征，假设维度为

Diagonal Covariance Gaussian 公式一：

Log-likelihood for diagonal covariance Gaussian 公式二：

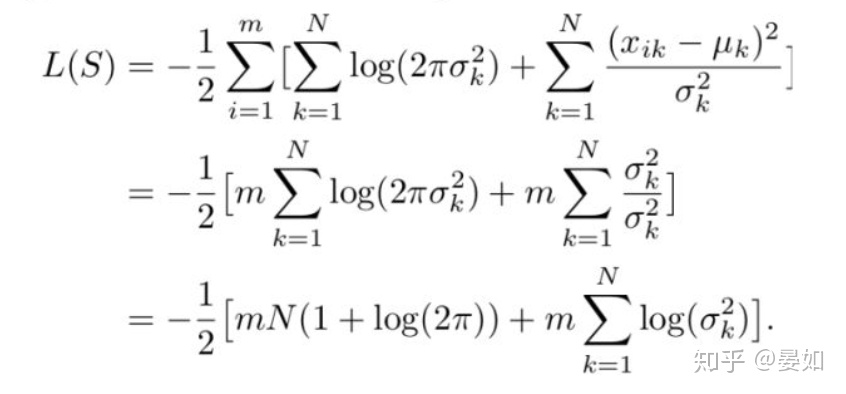
然后对根节点（比如{#-K+IY,1}） 选择某个问题，将其对应的observation Samples 集合

当然是似然增益最大的分法最好。似然增益越大，说明分裂之后的两个子集之间的差异越大。

将D的公式进行简化，则最优分法的问题称为最优问题，表示如下（下图第三个公式）。这样就解决了如何从问题集中选择问题进行分裂。

step 3: 选择当前所有待分裂的节点,重复step2，直至收敛

选择了增益最大的问题，将集合S一分为二之后，下一步如何选择节点、如何选择问题进行下一个分裂可以继续使用似然增益的准则，递归的执行该算法直至达到一定条件终止，通常是分裂已经达到一定数量的叶子节点，或者似然增益已经低于一定阈值。

初学者，文章是上网课的笔记，如果有错误请指出来。谢谢～