1、使用KNN算法对两个未知类型的样本进行分类（冰川水或者湖泊水），其中K=3，即选择最近的3个邻居。（20分）

学生答案：
解：
$Distance(G,A{)}^2=0.1;Distance(G,B{)}^2=0.03;Distance(G,C{)}^2=0.11$
$Distance(G,D{)}^2=0.12;Distance(G,E{)}^2=0.16;Distance(G,F{)}^2=0.05$
G的三个最近的邻居为B,F,A，因此G的分类为冰川水
$Distance(H,A{)}^2=0.03;Distance(H,B{)}^2=0.18;Distance(H,C{)}^2=0.22$
$Distance(H,D{)}^2=0.03;Distance(H,E{)}^2=0.21;Distance(H,F{)}^2=0.16$
H的三个最近的邻居为A,D,F，因此H的分类为湖泊水
2、使用CART决策树算法对两个未知类型的样本进行分类。（使用ID3决策树算法对两个未知类型的样本进行分类。）（20分）

CART算法：
对样本集S，计算其在各个属性划分上的基尼指数。
1）
$Gini(S,Ca+浓度)=4/8[1-(2/4{)}^2-(2/4{)}^2]+4/8[1-(2/4{)}^2-(2/4{)}^2]=0.5$
2）
$Gini(S,Mg+浓度)=4/8[1-(3/4{)}^2-(1/4{)}^2]+4/8[1-(1/4{)}^2-(3/4{)}^2]=0.375$
3）
$Gini(S,Na+浓度)=4/8[1-(2/4{)}^2-(2/4{)}^2]+4/8[1-(2/4{)}^2-(2/4{)}^2]=0.5$
4）
$Gini(S,Cl-浓度)=4/8[1-(2/4{)}^2-(2/4{)}^2]+4/8[1-(4/4{)}^2]=0.25$
Cl-浓度属性的基尼指数最小，将Cl-浓度属性作为第一个划分属性，将集合S划分为以下两个子集：
S1(高):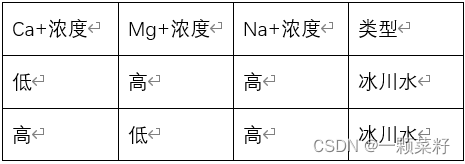

S2(低)：

对样本集S1，所有样本均属于同一类型：冰川水。
对样本集S2，计算其在各个属性划分上的基尼指数：
1）
$Gini(S2,Ca+浓度)=2/6[1-(1/2{)}^2-(1/2{)}^2]+4/6[1-(2/4{)}^2-(2/4{)}^2]=0.5$
2）
$Gini(S2,Mg+浓度)=2/6[1-(2/2{)}^2]+4/6[1-(3/4{)}^2-(1/4{)}^2]=0.25$
3）
$Gini(S2,Na+浓度)=2/6[1-(2/2{)}^2]+4/6[1-(2/4{)}^2-(2/4{)}^2]=0.333$
可以看出Gini(S2,Mg+浓度)最小，所以应该选择Mg+浓度属性作为测试属性。
Mg+浓度属性将样本集划分为两个子集:
1）S21

2）S22

对样本集S21，计算其在各个属性划分上的基尼指数：
1）
$Gini(S21,Ca+浓度)=2/3[1-(1/2{)}^2-(1/2{)}^2]+1/3[1-(1/1{)}^2]=0.333$
2）
$Gini(S21,Na+浓度)=2/3[1-(2/2{)}^2]+1/3[1-(1/1{)}^2]=0$
可以看出Gini(S2,Na+浓度)最小，所以应该选择Na+浓度浓度属性作为测试属性。
Na+浓度属性将样本集划分为两个子集, 并且各个子集中的样本都属于同一个类型。

对样本集S22，所有样本均属于同一类型湖泊水。
决策树构造完毕，如下图所示。

图1 选择Na+浓度作为节点
由上面决策树，得第一个待识别样本类型为湖泊水；第二个待识别样本类型为冰川水。
3、如下表所示的数据集，其在二维空间中的分布情况如图1所示，用户输入ε=1，MinPts=5，采用DBSCAN算法对表中数据进行聚类。(20分)

第一类：{1,3,4,5,10}
第二类：{2,6,7,8,11}

4、已知数据集如表1所示，使用朴素Bayes算法预测气候状况为雨天，高温，湿度中等。微风时，是否适合户外运动？（20分）
表1 数据集信息

解：
即求X={下雨，高，中等，威风}的户外运动为可以的后验概率P(Y=y|X)和为不可以的后验概率P(Y=n|X)两者值中较大者为X的预测值。
根据Bayes定理，
$$\begin{gathered} P(Y=y|X) \\ =P(X|Y=y)\ast P(Y=y) \\ =P(x_1|Y=y)\ast P(x_2|Y=y)\ast P(x_3|Y=y)\ast P(x_4|Y=y)\ast P(Y=y) \end{gathered}$$
这里，$P(x_1|Y=y)=P(x_1=下雨|Y=y)=3/6$
$P(x_2|Y=y)=P(x_2=高|Y=y)=1/6$
$P(x_3|Y=y)=P(x_3=中等|Y=y)=4/6$
$P(x_4|Y=y)=P(x_4=微风|Y=y)=5/6$
$P(Y=y)= 6/10 $
因此，$P(Y=y|X)=3/6\ast 1/6\ast 4/6\ast 5/6\ast 6/10=1/36$
同理，计算$P(Y=n|X)=P(X|Y=n)\ast P(Y=n)=P(x1|Y=n)\ast P(x2|Y=n)\ast P(x3|Y=n)\ast P(x4|Y=n)\ast P(Y=n)$
其中，
$P(x1|Y=n)=P(x1=下雨|Y=n)=1/4$
$P(x2|Y=n)=P(x2=高|Y=n)=2/4$
$P(x3|Y=n)=P(x3=中等|Y=n)=1/4$
$P(x4|Y=n)=P(x4=微风|Y=n)=2/4$
$P(Y=n)=4/10$
因此，$P(Y=n|X)=1/4\ast 2/4\ast 1/4\ast 2/4\ast 4/10=1/160$
因为$P(Y=y|X)>P(Y=n|X)$，故气候状况为雨天，高温，湿度中等，微风时，户外运动应为适合。

5、假如空间中的五个点{A,B,C,D,E}，各点之间的距离关系如表2所示，设初始聚类中心点为{A,B}，根据所给的数据对其运行K-中心点算法实现第一次迭代后的聚类划分结果及相应的两个中心点（K=2）。（20分）
样本点 A B C D E
A 0 1 2 3 4
B 1 0 3 5 2
C 2 3 0 1 4
D 3 5 1 0 6
E 4 2 4 6 0

根据已知条件，当两个初始中心点为{A,B}时，所得划分为{A,C,D}和{B,E}。
第一次迭代：
假定中心点{A,B}分别被非中心点{C,D,E}替换，根据K-中心点算法需要计算下列代价：$T{C}_{AC}$、$T{C}_{AD}$、$T{C}_{AE}、T{C}_{BC}、T{C}_{BD}和T{C}_{BE}$。其中$T{C}_{AC}$表示中心点A被非中心点C代替后的总代价。下面以$T{C}_{AC}$为例说明计算过程。
当A被C代替后，看各对象的变化情况。
A：因A离B近，$C_{AAC}=d(A,B)-d(A,A)=1-0=1。$
B：B不受影响，$C_{BAC}=0$。
C：$C_{CAC}=d(C,C)-d(C,A)=0-2=-2$。
D：$C_{DAC}=d(D,C)-d(D,A)=1-3=-2$。
E：$C_{EAC}=0$。
于是，$T{C}_{AC}=C_{AAC}+C_{BAC}+C_{CAC}+C_{DAC}+C_{EAC}=1+0-2-2+0=-3$。同理，可以计算出：$T{C}_{AD}=-3，T{C}_{AE}=2，T{C}_{BC}=-1，T{C}_{BD}=-1，T{C}_{BE}=-1$。
选取最小代价，有两种选择。
选取$T{C}_{AC}$为最小代价时，则两个中心点为{B,C}，样本被重新划分为{ A,B,E}和{C,D}两个簇。
选取$T{C}_{AD}$为最小代价时，则两个中心点为{B,D}，样本被重新划分为{ A,B,E}和{C,D}两个簇。