开源项目地址：d2l-ai/d2l-zh

教材官网：https://zh.d2l.ai/

书介绍：https://zh-v2.d2l.ai/

笔记基于2021年7月26日发布的版本，书及代码下载地址在github网页的最下面

交流者论坛

额外：
https://distill.pub/

pytorch中文文档（哪个函数不明白用法查询非常好用）

---

（d2l-ai/d2l-zh）《动手学深度学习》pytorch 笔记（1）（序言、pytorch的安装、神经网络涉及符号）

（d2l-ai/d2l-zh）《动手学深度学习》pytorch 笔记（2）前言（介绍各种机器学习问题）

2.3 线性代数

2.3.1 标量（68）

严格来说，我们称仅包含⼀个数值的叫标量（scalar）如果要将此华⽒度值转换为更常⽤的摄⽒度，则可以计算表达式c =59(f − 32)，并将f赋为52。在此等式中，每⼀项（5、9和32）都是标量值。符号c和f称为变量（variables），它们表⽰未知的标量值。

表达式x ∈ R是表⽰x是⼀个实值标量的正式形式。符号∈称为“属于”，它表⽰“是集合中的成员”。我们可以⽤x, y ∈ {0, 1}来表明x和y是值只能为0或1的数字。

标量由只有⼀个元素的张量表⽰。

2.3.2 向量（69）

你可以将向量视为标量值组成的列表。

我们将这些标量值称为向量的元素（elements）或分量（components）。

当我们的向量表⽰数据集中的样本时，它们的值具有⼀定的现实意义。

例如，如果我们正在训练⼀个模型来预测贷款违约⻛险，我们可能会将每个申请⼈与⼀个向量相关联，其分量与其收⼊、⼯作年限、过往违约次数和其他因素相对应。如果我们正在研究医院患者可能⾯临的⼼脏病发作⻛险，我们可能会⽤⼀个向量来表⽰每个患者，其分量为最近的⽣命体征、胆固醇⽔平、每天运动时间等。

在数学表⽰法中，我们通常将向量记为粗体、小写的符号（例如，x、y和z)）。

在数学中，向量x可以写为：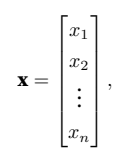

在代码中，我们通过张量的索引来访问任⼀元素：

import torch

x = torch.arange(4)
print(x[1])  # tensor(1)

长度（dimension）、维度（dimension）和形状（shape）（69）（这里的维跟我们平时所说的几维空间的维还不一样！）（向量或轴的维度被⽤来表⽰向量或轴的长度，即向量或轴的元素数量。然而，张量的维度⽤来表⽰张量具有的轴数。在这个意义上，张量的某个轴的维数就是这个轴的长度。）

向量的⻓度通常称为向量的维度（dimension）

我们可以通过调⽤Python的内置len()函数来访问张量的⻓度：

import torch

x = torch.arange(4)
print(len(x))   # 4

形状（shape）是⼀个元组，列出了张量沿每个轴（axis）的⻓度（维数）。对于只有⼀个轴的张量，形状只有⼀个元素。

2.3.3 矩阵（70）

在数学表⽰法中，我们使⽤A ∈ Rm×n来表⽰矩阵A，其由m⾏和n列的实值标量组成。直观地，我们可以将任意矩阵A ∈ Rm×n视为⼀个表格，其中每个元素aij属于第i⾏第j列：

对于任意A ∈ Rm×n,A的形状是(m, n)或m × n。当矩阵具有相同数量的⾏和列时，其形状将变为正⽅形；因此，它被称为方矩阵（square matrix）。

当调⽤函数来实例化张量时，我们可以通过指定两个分量m和 n来创建⼀个形状为m × n的矩阵。

import torch

A = torch.arange(20).reshape(5, 4)

print(A)
# tensor([[ 0,  1,  2,  3],
#         [ 4,  5,  6,  7],
#         [ 8,  9, 10, 11],
#         [12, 13, 14, 15],
#         [16, 17, 18, 19]])

有时候，我们想翻转轴。当我们交换矩阵的⾏和列时，结果称为矩阵的转置（transpose）。

我们⽤a⊤来表⽰矩阵的转置，如果B = A⊤，则对于任意i和j，都有bij = aji。

在代码中访问矩阵的转置：

import torch

A = torch.arange(20).reshape(5, 4)

print(A.T)
# tensor([[ 0,  4,  8, 12, 16],
#         [ 1,  5,  9, 13, 17],
#         [ 2,  6, 10, 14, 18],
#         [ 3,  7, 11, 15, 19]])

作为⽅矩阵的⼀种特殊类型，对称矩阵（symmetric matrix）A等于其转置：A = A⊤。

import torch

B = torch.tensor([[1, 2, 3], [2, 0, 4], [3, 4, 5]])

print(B)
# tensor([[1, 2, 3],
#         [2, 0, 4],
#         [3, 4, 5]])

print(B == B.T)
# tensor([[True, True, True],
#         [True, True, True],
#         [True, True, True]])

矩阵是有⽤的数据结构：它们允许我们组织具有不同变化模式的数据。例如，我们矩阵中的⾏可能对应于不同的房屋（数据样本），而列可能对应于不同的属性。如果你曾经使⽤过电⼦表格软件或已阅读过 2.2节，这应该听起来很熟悉。因此，尽管单个向量的默认⽅向是列向量，但在表示意表格数据集的矩阵中，将每个数据样本作为矩阵中的⾏向量更为常见。我们将在后⾯的章节中讲到这点。这种约定将⽀持常⻅的深度学习实践。例如，沿着张量的最外轴，我们可以访问或遍历小批量的数据样本。如果不存在小批量，我们也可以只访问
数据样本。

2.3.4 张量（72）

当我们开始处理图像时，张量将变得更加重要，图像以n维数组形式出现，其中3个轴对应于⾼度、宽度，以及⼀个通道（channel）轴，⽤于堆叠颜⾊通道（红⾊、绿⾊和蓝⾊）。

import torch

X = torch.arange(24).reshape(2, 3, 4)

print(X)
# tensor([[[ 0,  1,  2,  3],
#          [ 4,  5,  6,  7],
#          [ 8,  9, 10, 11]],
#
#         [[12, 13, 14, 15],
#          [16, 17, 18, 19],
#          [20, 21, 22, 23]]])

2.3.5 张量算法的基本性质（72）张量加法（张量加张量、张量加标量）、哈达玛积（Hadamard product）、张量乘标量

你可能已经从按元素操作的定义中注意到，任何按元素的⼀元运算都不会改变其操作数的形状。同样，给定具有相同形状的任意两个张量，任何按元素⼆元运算的结果都将是相同形状的张量。

例如，将两个相同形状的矩阵相加会在这两个矩阵上执⾏元素加法：

import torch

A = torch.arange(20, dtype=torch.float32).reshape(5, 4)
B = A.clone()  # 通过分配新内存，将A的⼀个副本分配给B

print(A)
# tensor([[ 0.,  1.,  2.,  3.],
#         [ 4.,  5.,  6.,  7.],
#         [ 8.,  9., 10., 11.],
#         [12., 13., 14., 15.],
#         [16., 17., 18., 19.]])

print(A + B)
# tensor([[ 0.,  2.,  4.,  6.],
#         [ 8., 10., 12., 14.],
#         [16., 18., 20., 22.],
#         [24., 26., 28., 30.],
#         [32., 34., 36., 38.]])

具体而⾔，两个矩阵的按元素乘法称为哈达玛积（Hadamard product）（哈德蒙德？）（数学符号⊙）。对于矩阵B ∈ Rm×n，其中第i⾏和第j列的元素是bij。矩阵A（在 (2.3.2)中定义）和B的哈达玛积为：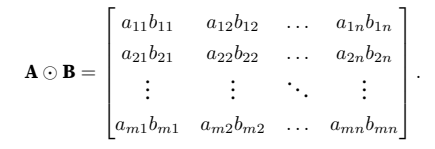

import torch

A = torch.arange(20, dtype=torch.float32).reshape(5, 4)
B = A.clone()  # 通过分配新内存，将A的⼀个副本分配给B

print(A * B)
# tensor([[  0.,   1.,   4.,   9.],
#         [ 16.,  25.,  36.,  49.],
#         [ 64.,  81., 100., 121.],
#         [144., 169., 196., 225.],
#         [256., 289., 324., 361.]])

• 将张量乘以或加上⼀个标量不会改变张量的形状，其中张量的每个元素都将与标量相加或相乘。

import torch

A = torch.arange(20, dtype=torch.float32).reshape(5, 4)
a = 2
print(a + A)
# tensor([[ 2.,  3.,  4.,  5.],
#         [ 6.,  7.,  8.,  9.],
#         [10., 11., 12., 13.],
#         [14., 15., 16., 17.],
#         [18., 19., 20., 21.]])

print(a * A)
# tensor([[ 0.,  2.,  4.,  6.],
#         [ 8., 10., 12., 14.],
#         [16., 18., 20., 22.],
#         [24., 26., 28., 30.],
#         [32., 34., 36., 38.]])

2.3.6 降维（73）（求向量元素和）

我们可以对任意张量进⾏的⼀个有⽤的操作是计算其元素的和。在数学表⽰法中，我们使⽤∑符号表⽰求和。为了表⽰⻓度为d的向量中元素的总和，可以记为∑di=1 xi。在代码中，我们可以调⽤计算求和的函数：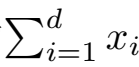

import torch

x = torch.arange(4, dtype=torch.float32)
print(x)    # tensor([0., 1., 2., 3.])
print(x.sum())  # tensor(6.)

我们可以表⽰任意形状张量的元素和。例如，矩阵A中元素的和可以记为∑m
i=1∑nj=1 aij。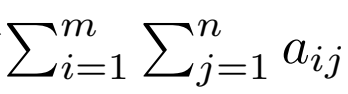

默认情况下，调⽤求和函数会沿所有的轴降低张量的维度，使它变为⼀个标量。我们还可以指定张量沿哪⼀个轴来通过求和降低维度。以矩阵为例，为了通过求和所有⾏的元素来降维（轴0），我们可以在调⽤函数时指定axis=0。由于输⼊矩阵沿0轴降维以⽣成输出向量，因此输⼊的轴0的维数在输出形状中丢失。

import torch

A = torch.arange(20, dtype=torch.float32).reshape(5, 4)

A_sum_axis0 = A.sum(axis=0)
A_sum_axis1 = A.sum(axis=1)

print(A)
# tensor([[ 0.,  1.,  2.,  3.],
#         [ 4.,  5.,  6.,  7.],
#         [ 8.,  9., 10., 11.],
#         [12., 13., 14., 15.],
#         [16., 17., 18., 19.]])
print(A_sum_axis0)  # tensor([40., 45., 50., 55.])
print(A_sum_axis1)  # tensor([ 6., 22., 38., 54., 70.])

# 沿着⾏和列对矩阵求和，等价于对矩阵的所有元素进⾏求和。
print(A.sum(axis=[0, 1]))  # tensor(190.)

# ⼀个与求和相关的量是平均值（mean或average）。我们通过将总和除以元素总数来计算平均值。在代码中，
# 我们可以调⽤函数来计算任意形状张量的平均值。
print(A.mean())  # tensor(9.5000)
print(A.sum() / A.numel())  # tensor(9.5000)

# 同样，计算平均值的函数也可以沿指定轴降低张量的维度
print(A.mean(axis=0))  # tensor([ 8.,  9., 10., 11.])  （想象撸串）
print(A.sum(axis=0) / A.shape[0])   # tensor([ 8.,  9., 10., 11.])

非降维求和（保持轴数不变keepdims =）（ tensor.cumsum()计算沿某轴累计和）（74）

但是，有时在调⽤函数来计算总和或均值时保持轴数不变会很有用

import torch

A = torch.arange(20, dtype=torch.float32).reshape(5, 4)

sum_A = A.sum(axis=1, keepdims=True)
sum_A_ = A.sum(axis=1, keepdims=False)

print(A)
# tensor([[ 0.,  1.,  2.,  3.],
#         [ 4.,  5.,  6.,  7.],
#         [ 8.,  9., 10., 11.],
#         [12., 13., 14., 15.],
#         [16., 17., 18., 19.]])
print(sum_A)
# tensor([[ 6.],
#         [22.],
#         [38.],
#         [54.],
#         [70.]])
print(sum_A_)
# tensor([ 6., 22., 38., 54., 70.])

# 例如，由于sum_A在对每⾏进⾏求和后仍保持两个轴，我们可以通过⼴播将A除以sum_A。（得到每个元素所占各自行的百分比）
print(A/sum_A)
# tensor([[0.0000, 0.1667, 0.3333, 0.5000],
#         [0.1818, 0.2273, 0.2727, 0.3182],
#         [0.2105, 0.2368, 0.2632, 0.2895],
#         [0.2222, 0.2407, 0.2593, 0.2778],
#         [0.2286, 0.2429, 0.2571, 0.2714]])

• tensor.cumsum()计算沿某轴累计和

如果我们想沿某个轴计算A元素的累积总和，⽐如axis=0（按⾏计算），我们可以调⽤cumsum函数。此函数不会沿任何轴降低输⼊张量的维度。

import torch

A = torch.arange(20, dtype=torch.float32).reshape(5, 4)

print(A.cumsum(axis=0))
# tensor([[ 0.,  1.,  2.,  3.],
#         [ 4.,  6.,  8., 10.],
#         [12., 15., 18., 21.],
#         [24., 28., 32., 36.],
#         [40., 45., 50., 55.]])

2.3.7 点积（Dot Product）（torch.dot(x, y)）(torch.sum(x * y))（75）

import torch

x = torch.arange(4, dtype=torch.float32)
y = torch.ones(4, dtype=torch.float32)

print(x)    # tensor([0., 1., 2., 3.])
print(y)    # tensor([1., 1., 1., 1.])
print(torch.dot(x, y))  # tensor(6.)

# 注意，我们也可以通过执⾏按元素乘法，然后进⾏求和来表⽰两个向量的点积：
print(torch.sum(x * y)) # tensor(6.)

2.3.8 矩阵-向量积（还是dot函数，不过是np.dot()不是torch.dot()，也可以用torch.mv()函数替代）（76）

我们可以把⼀个矩阵A ∈ Rm×n乘法看作是⼀个从Rn到Rm向量的转换。这些转换证明是⾮常有⽤的。例如，我们可以⽤⽅阵的乘法来表⽰旋转。我们将在后续章节中讲到，我们也可以使⽤矩阵-向量积来描述在给定前⼀层的值时，求解神经⽹络每⼀层所需的复杂计算。

在代码中使⽤张量表⽰矩阵-向量积，我们使⽤与点积相同的dot函数。当我们为矩阵A和向量x调⽤np.dot(A,x)时，会执⾏矩阵-向量积。注意，A的列维数（沿轴1的⻓度）必须与x的维数（其⻓度）相同。

import torch
import numpy as np

A = torch.arange(20, dtype=torch.float32).reshape(5, 4)
x = torch.arange(4, dtype=torch.float32)

print(A)
# tensor([[ 0.,  1.,  2.,  3.],
#         [ 4.,  5.,  6.,  7.],
#         [ 8.,  9., 10., 11.],
#         [12., 13., 14., 15.],
#         [16., 17., 18., 19.]])
print(x)    # tensor([0., 1., 2., 3.])
print(np.dot(A, x))     # [ 14.  38.  62.  86. 110.]
print(torch.mv(A, x))   # tensor([ 14.,  38.,  62.,  86., 110.])

mv是啥函数啊？在哪看文档？？

---

妈蛋，这可以查到pytorch函数中文文档，这么简单！

2.3.9 矩阵-矩阵乘法（torch.mm）（77）

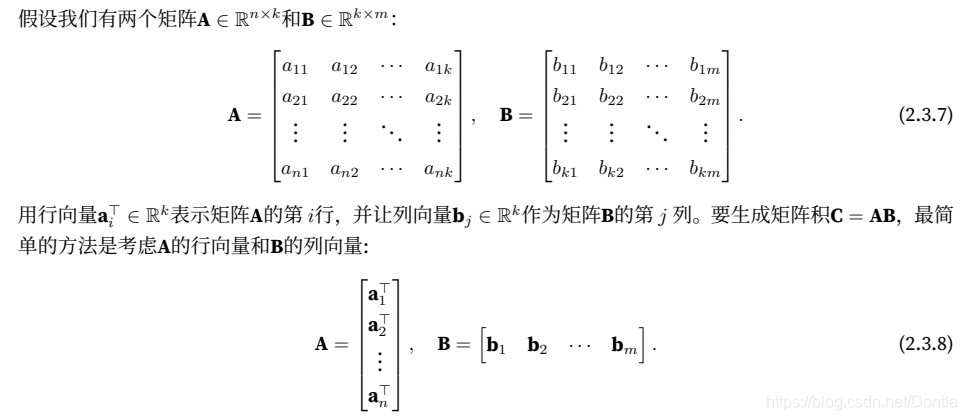
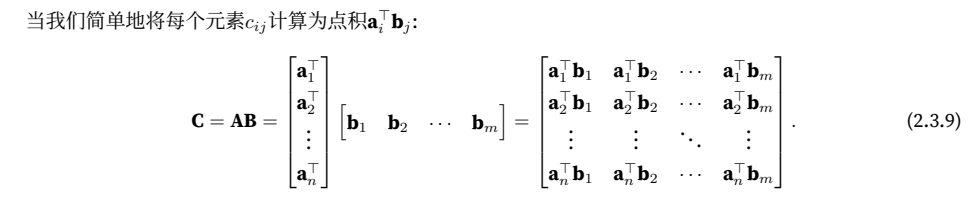
我们可以将矩阵-矩阵乘法AB看作是简单地执⾏m次矩阵-向量积，并将结果拼接在⼀起，形成⼀个n × m矩阵。在下⾯的代码中，我们在A和B上执⾏矩阵乘法。这⾥的A是⼀个5⾏4列的矩阵，B是⼀个4⾏3列的矩阵。相乘后，我们得到了⼀个5⾏3列的矩阵。

import torch

A = torch.arange(20, dtype=torch.float32).reshape(5, 4)
B = torch.ones(4, 3)

print(torch.mm(A, B))
# tensor([[ 6.,  6.,  6.],
#         [22., 22., 22.],
#         [38., 38., 38.],
#         [54., 54., 54.],
#         [70., 70., 70.]])

矩阵-矩阵乘法可以简单地称为矩阵乘法，不应与“哈达玛积”混淆。

2.3.10 范数（78）（L2范数与L1范数、弗罗贝尼乌斯范数）（L2范数就是弗罗贝尼乌斯范数？）（torch.norm）（绝对值函数torch.abs）

线性代数中最有⽤的⼀些运算符是范数（norms）。⾮正式地说，⼀个向量的范数告诉我们⼀个向量有多⼤。这⾥考虑的⼤小（size）概念不涉及维度，而是分量（指向量中每个元素？）的⼤小。

在线性代数中，向量范数是将向量映射到标量的函数f。向量范数要满⾜⼀些属性。给定任意向量x，第⼀个性质说，如果我们按常数因⼦α缩放向量的所有元素，其范数也会按相同常数因⼦的绝对值缩放：

f(αx) = |α|f(x).
第⼆个性质是我们熟悉的三⻆不等式:
f(x + y) ≤ f(x) + f(y).
第三个性质简单地说范数必须是⾮负的:
f(x) ≥ 0.
这是有道理的，因为在⼤多数情况下，任何东西的最小的⼤小是0。最后⼀个性质要求范数最小为0，当且仅当向量全由0组成。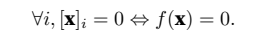

（倒A为每一个的意思，全部）
你可能会注意到，范数听起来很像距离的度量。如果你还记得小学时的欧⼏⾥得距离(想想毕达哥拉斯定理【勾股定理】)，那么⾮负性的概念和三⻆不等式可能会给你⼀些启发。事实上，欧⼏⾥得距离是⼀个范数：具体而⾔，它是L2范数。假设n维向量x中的元素是x1, . . . , xn，其L2范数是向量元素平⽅和的平⽅根：

欧几里得度量

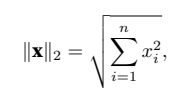
其中，在L2范数中常常省略下标2，也就是说，∥x∥等同于∥x∥2。在代码中，我们可以按如下⽅式计算向量的L2范数。

import torch
u = torch.tensor([3.0, -4.0])
print(torch.norm(u))    # tensor(5.)

在深度学习中，我们更经常地使⽤L2范数的平⽅。你还会经常遇到L1范数，它表⽰为向量元素的绝对值之和：

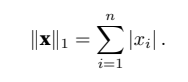
与L2范数相⽐，L1范数受异常值的影响较小。为了计算L1范数，我们将绝对值函数和按元素求和组合起来。

import torch
u = torch.tensor([3.0, -4.0])
print(torch.abs(u).sum())   # tensor(7.)

L2范数和L1范数都是更⼀般的Lp范数的特例：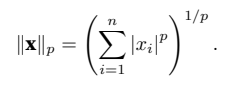

类似于向量的L2范数，矩阵X ∈ Rm×n的弗罗⻉尼乌斯范数（Frobenius norm）是矩阵元素平⽅和的平⽅根：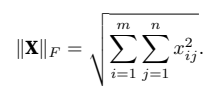

弗罗⻉尼乌斯范数满⾜向量范数的所有性质，它就像是矩阵形向量的L2范数。调⽤以下函数将计算矩阵的弗罗⻉尼乌斯范数。

import torch
print(torch.norm(torch.ones((4, 9))))   # tensor(6.)    根号36等于6

范数和目标（79）

虽然我们不想走得太远，但我们可以对这些概念为什么有⽤有⼀些直觉。在深度学习中，我们经常试图解决优化问题：最⼤化分配给观测数据的概率; 最小化预测和真实观测之间的距离。⽤向量表⽰物品(如单词、产品或新闻⽂章)，以便最小化相似项⽬之间的距离，最⼤化不同项⽬之间的距离。通常，⽬标，或许是深度学习算法最重要的组成部分(除了数据)，被表达为范数。

2.3.11 关于线性代数的更多信息（79）

仅⽤⼀节，我们就教会了你所需的，⽤以理解⼤量的现代深度学习的全部线性代数。线性代数还有很多，其中很多数学对于机器学习⾮常有⽤。例如，矩阵可以分解为因⼦，这些分解可以显⽰真实世界数据集中的低维结构。机器学习的整个⼦领域都侧重于使⽤矩阵分解及其向⾼阶张量的泛化来发现数据集中的结构并解决预测问题。

2.3.12 ⼩结（80）

• 标量、向量、矩阵和张量是线性代数中的基本数学对象。
• 向量泛化⾃标量，矩阵泛化⾃向量。
• 标量、向量、矩阵和张量分别具有零、⼀、⼆和任意数量的轴。
• ⼀个张量可以通过sum和mean沿指定的轴降低维度。
• 两个矩阵的按元素乘法被称为他们的哈达玛积。它与矩阵乘法不同。
• 在深度学习中，我们经常使⽤范数，如L1范数、L2范数和弗罗⻉尼乌斯范数。
• 我们可以对标量、向量、矩阵和张量执⾏各种操作。

2.4 微分（80）

逼近法（method of exhaustion）（80）

积分（integral calculus）

微分（differential calculus）

损失函数（loss function）

我们可以将拟合模型的任务分解为两个关键问题：
（1）优化（optimization）：⽤模型拟合观测数据的过程；
（2）泛化（generalization）：数学原理和实践者的智慧，能够指导我们⽣成出有效性超出⽤于训练的数据集本⾝的模型。

2.4.1 导数和微分（81）（matplotlib函数使用）（★绘制二次函数和它的切线）

在深度学习中，我们通常选择对于模型参数可微的损失函数。简而⾔之，这意味着，对于每个参数，如果我们把这个参数增加或减少⼀个⽆穷
小的量，我们可以知道损失会以多快的速度增加或减少，

假设我们有⼀个函数f : Rn → R，其输⼊和输出都是标量。f的导数被定义为：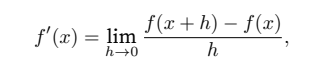

如果这个极限存在。如果f′(a)存在，则称f在a处是可微（differentiable）的。如果f在⼀个区间内的每个数上都是可微的，则此函数在此区间中是可微的。我们可以将 (2.4.1)中的导数f′(x)解释为f(x)相对于x的瞬时（instantaneous）变化率。所谓的瞬时变化率是基于x中的变化h，且h接近0。

为了更好地解释导数，让我们⽤⼀个例⼦来做实验。定义u = f(x) = 3 * x^2 − 4 * x

import numpy as np
from IPython import display
from d2l import torch as d2l


def f(x):
    return 3 * x ** 2 - 4 * x


def numerical_lim(func, x, t):
    return (func(x + t) - func(x)) / t


h = 0.1
for i in range(5):
    print(f'h={h:.5f}, numerical limit={numerical_lim(f, 1, h):.5f}')
    h *= 0.1

运行结果：

h=0.10000, numerical limit=2.30000
h=0.01000, numerical limit=2.03000
h=0.00100, numerical limit=2.00300
h=0.00010, numerical limit=2.00030
h=0.00001, numerical limit=2.00003

为了对导数的这种解释进⾏可视化，我们将使⽤matplotlib，这是⼀个Python中流⾏的绘图库。要配置matplotlib⽣成图形的属性，我们需要定义⼏个函数。

• 定义use_svg_display函数指定matplotlib软件包输出svg图表以获得更清晰的图像。

注意，注释#@save是⼀个特殊的标记，会将对应的函数、类或语句保存在d2l包中因此，以后⽆需重新定义就可以直接调⽤它们（例如，d2l.use_svg_display()）。

• 定义set_figsize函数来设置图表⼤小。注意，这⾥我们直接使⽤d2l.plt，因为导⼊语句 from matplotlib import pyplot as plt已在前⾔中标记为保存到d2l包中。（啥意思？？它是重新封装了一个？）

• 定义set_axes函数⽤于设置由matplotlib⽣成图表的轴的属性。

通过这三个⽤于图形配置的函数，我们定义了plot函数来简洁地绘制多条曲线，因为我们需要在整个书中可视化许多曲线。

现在我们可以绘制函数u = f(x)及其在x = 1处的切线y = 2x − 3，其中系数2是切线的斜率。

pycharm代码：

import numpy as np
from IPython import display
from d2l import torch as d2l


def use_svg_display():  # @save
    """使⽤svg格式在Jupyter中显⽰绘图。"""
    display.set_matplotlib_formats('svg')


def set_figsize(figsize=(3.5, 2.5)):  # @save
    """设置matplotlib的图表⼤⼩。"""
    # use_svg_display()
    d2l.plt.rcParams['figure.figsize'] = figsize


# @save
def set_axes(axes, xlabel, ylabel, xlim, ylim, xscale, yscale, legend):
    """设置matplotlib的轴。"""
    axes.set_xlabel(xlabel)
    axes.set_ylabel(ylabel)
    axes.set_xscale(xscale)
    axes.set_yscale(yscale)
    axes.set_xlim(xlim)
    axes.set_ylim(ylim)
    if legend:
        axes.legend(legend)
    axes.grid() # 绘制刻度线的网格线？


# @save
def plot(X, Y=None, xlabel=None, ylabel=None, legend=None, xlim=None,
         ylim=None, xscale='linear', yscale='linear',
         fmts=('-', 'm--', 'g-.', 'r:'), figsize=(3.5, 2.5), axes=None):
    """绘制数据点。"""
    if legend is None:
        legend = []
    set_figsize(figsize)
    axes = axes if axes else d2l.plt.gca()

    # 如果 `X` 有⼀个轴，输出True
    def has_one_axis(X):
        # hasattr返回object对象是否有name属性（判断X是否有ndim属性）（从调试新建观察点看还真有ndim属性，且ndim == 1）（has attribute的缩写）
        # isinstance函数判断数据类型
        # hasattr(X, "ndim") 是True，X.ndim == 1是True，isinstance(X, list)是False，hasattr(X[0], "__len__")是False
        return hasattr(X, "ndim") and X.ndim == 1 or isinstance(X, list) and not hasattr(X[0], "__len__")

    if has_one_axis(X):
        X = [X] # 把X转换成列表？
    if Y is None:
        X, Y = [[]] * len(X), X # 啥意思？
    elif has_one_axis(Y):   # len(f(x))的结果是个列表，长度是30
        Y = [Y]
    if len(X) != len(Y):
        X = X * len(Y)  # 就是说如果Y有多个函数的话，要把X扩充跟Y一样多，那样才能画图
    axes.cla()  # Clear axis即清除当前图形中的当前活动轴。其他轴不受影响。
    for x, y, fmt in zip(X, Y, fmts):   # zip是将三组元素打包，然后三个三个取出用于画图
        if len(x):  # 如果x的长度大于0
            axes.plot(x, y, fmt)
        else:
            axes.plot(y, fmt)   # 跟x无关，y等于常数？
    set_axes(axes, xlabel, ylabel, xlim, ylim, xscale, yscale, legend)


def f(i):
    return 3 * i ** 2 - 4 * i


if __name__ == '__main__':
    x = np.arange(0, 3, 0.1)

    # 第二个参数为什么提示：Expected type 'Optional[{ndim, __getitem__, __len__}]', got 'List[Union[int, Any]]' instead
    plot(x, [f(x), 2 * x - 3], 'x', 'f(x)', legend=['f(x)', 'Tangent line (x=1)'])
    d2l.plt.show()

运行结果：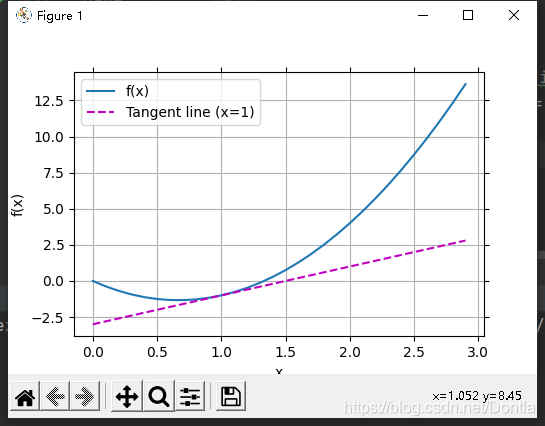

2.4.2 偏导数（partial derivative）（85）

到⽬前为⽌，我们只讨论了仅含⼀个变量的函数的微分。在深度学习中，函数通常依赖于许多变量。因此，我们需要将微分的思想推⼴到这些多元函数（multivariate function）上。

设y = f(x1, x2, . . . , xn)是⼀个具有n 个变量的函数。y关于第i个参数xi的偏导数（partial derivative）为：

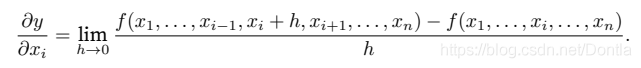
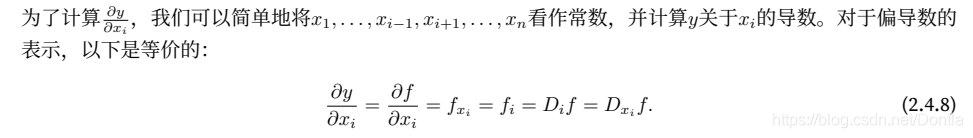
2.4.3 梯度（85）

2.4.4 链式法则（85）

然而，上⾯⽅法可能很难找到梯度。这是因为在深度学习中，多元函数通常是复合（composite）的，所以我们可能没法应⽤上述任何规则来微分这些函数。幸运的是，链式法则使我们能够微分复合函数。

让我们先考虑单变量函数。假设函数y = f(u)和u = g(x)都是可微的，根据链式法则：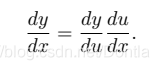

现在让我们把注意⼒转向⼀个更⼀般的场景，即函数具有任意数量的变量的情况。假设可微分函数y有变量u1, u2, . . . , um，其中每个可微分函数ui都有变量x1, x2, . . . , xn。注意，y是x1, x2 . . . , xn的函数。对于任意i = 1, 2, . . . , n，链式法则给出：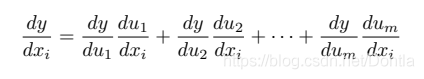

反向传播链式法则：简单@！

2.4.5 小结（86）

• 微分和积分是微积分的两个分⽀，其中前者可以应⽤于深度学习中⽆处不在的优化问题。
• 导数可以被解释为函数相对于其变量的瞬时变化率。它也是函数曲线的切线的斜率。
• 梯度是⼀个向量，其分量是多变量函数相对于其所有变量的偏导数。
• 链式法则使我们能够微分复合函数。

2.4.6 练习（86）

https://discuss.d2l.ai/t/topic/1756

2.5 自动求导（automatic differentiation）（我们为什么需要深度学习框架：能帮我们自动求导，手动求导是非常麻烦且容易出错的） （86）

深度学习框架通过⾃动计算导数，即⾃动求导（automatic differentiation）。

实际中，根据我们设计的模型，系统会构建⼀个计算图（computational graph），来跟踪计算是哪些数据通过哪些操作组合起来产⽣输出。⾃动求导使系统能够随后反向传播梯度。这⾥，反向传播（backpropagate）只是意味着跟
踪整个计算图，填充关于每个参数的偏导数。

2.5.1 ⼀个简单的例⼦（.requires_grad_）（.backward()（.grad））（87）

在我们计算y关于x的梯度之前，我们需要⼀个地⽅来存储梯度。重要的是，我们不会在每次对⼀个参数求导时都分配新的内存。因为我们经常会成千上万次地更新相同的参数，每次都分配新的内存可能很快就会将内存耗尽。注意，标量函数关于向量x的梯度是向量，并且与x具有相同的形状。

requires_grad:

每个变量都有两个标志：requires_grad和volatile。它们都允许从梯度计算中精细地排除子图，并可以提高效率。
requires_grad
如果有一个单一的输入操作需要梯度，它的输出也需要梯度。相反，只有所有输入都不需要梯度，输出才不需要。如果其中所有的变量都不需要梯度进行，后向计算不会在子图中执行。

import torch

x = torch.arange(4.0)
print(x)  # tensor([0., 1., 2., 3.])
x.requires_grad_(True)  # 等价于 `x = torch.arange(4.0, requires_grad=True)`
print(x.grad)  # None

y = 2 * torch.dot(x, x)  # 计算两个张量的点乘(内乘),两个张量都为1-D 向量.
print(y)  # tensor(28., grad_fn=<MulBackward0>)

# x是⼀个⻓度为4的向量，计算x和x的内积，得到了我们赋值给y的标量输出。接下来，我们可以通过调⽤反
# 向传播函数来⾃动计算y关于x每个分量的梯度，并打印这些梯度。
y.backward()  # 反向传播一次？
print(x.grad)  # tensor([ 0.,  4.,  8., 12.])

# 函数y = 2 * torch.dot(x, x)关于x的梯度应为4x。让我们快速验证我们想要的梯度是否正确计算。
print(x.grad == 4 * x)  # tensor([True, True, True, True])

# 现在让我们计算x的另⼀个函数。
# 在默认情况下，PyTorch会累积梯度，我们需要清除之前的值
x.grad.zero_()
y = x.sum()
y.backward()
print(x.grad)   # tensor([1., 1., 1., 1.])

2.5.2 ⾮标量变量的反向传播（x.grad.zero_()将保存的梯度清零）（backward函数的gradient参数）（88）

当y不是标量时，向量y关于向量x的导数的最⾃然解释是⼀个矩阵。对于⾼阶和⾼维的y和x，求导的结果可以是⼀个⾼阶张量。

然而，虽然这些更奇特的对象确实出现在⾼级机器学习中（包括深度学习中），但当我们调⽤向量的反向计算时，我们通常会试图计算⼀批训练样本中每个组成部分的损失函数的导数。这⾥，我们的⽬的不是计算微分矩阵，而是批量中每个样本单独计算的偏导数之和。（？）

import torch

x = torch.arange(4.0)
print(x)  # tensor([0., 1., 2., 3.])
x.requires_grad_(True)  # 等价于 `x = torch.arange(4.0, requires_grad=True)`
print(x.grad)  # None

# 对⾮标量调⽤`backward`需要传⼊⼀个`gradient`参数，该参数指定微分函数关于`self`的梯度。在我们的例⼦
# 中，我们只想求偏导数的和，所以传递⼀个1的梯度是合适的
y = x * x
# 等价于y.backward(torch.ones(len(x)))或者y.backward(torch.ones_like(x))或者y.backward(torch.tensor([1,1,1,1]))
y = y.sum()
print(y)    # tensor(14., grad_fn=<SumBackward0>)
y.backward()
print(x.grad)   # tensor([0., 2., 4., 6.])

为什么要设置backward函数的gradient参数为torch.tensor([1,1,1,1])？当然你也可以设置成[1,1,1,2]，那样的话结果grad的第四个数就要*2，结果就变成tensor([0., 2., 4., 12.])

y向x求偏导，，先求和再求偏导？还得再实践实践，有点懵逼

上面代码中“我们只想求偏导数的和，所以传递⼀个1的梯度是合适的”，那个“和”指的是什么？

2.5.3 分离计算（将中间结果分离为常数，用于其他或后续计算）（88）

有时，我们希望将某些计算移动到记录的计算图之外。例如，假设y是作为x的函数计算的，而z则是作为y和x的函数计算的。现在，想象⼀下，我们想计算z关于x的梯度，但由于某种原因，我们希望将y视为⼀个常数，并且只考虑到x在y被计算后发挥的作⽤。

在这⾥，我们可以分离y来返回⼀个新变量u，该变量与y具有相同的值，但丢弃计算图中如何计算y的任何信息。换句话说，梯度不会向后流经u到x。因此，下⾯的反向传播函数计算z=ux关于x的偏导数，同时将u作为常数处理，而不是z=xx*x关于x的偏导数。

import torch

x = torch.arange(4.0)
print(x)  # tensor([0., 1., 2., 3.])
x.requires_grad_(True)  # 等价于 `x = torch.arange(4.0, requires_grad=True)`
print(x.grad)  # None

y = x * x
print(y)    # tensor([0., 1., 4., 9.], grad_fn=<MulBackward0>)
u = y.detach()
print(u)    # # tensor([0., 1., 4., 9.])
z = u * x
z.sum().backward()
print(x.grad)   # tensor([0., 1., 4., 9.])

# 由于记录了y的计算结果，我们可以随后在y上调⽤反向传播，得到y=x*x关于的x的导数，这⾥是2*x。
x.grad.zero_()
y.sum().backward()
print(x.grad)   # tensor([0., 2., 4., 6.])

2.5.4 Python控制流（条件、循环或任意函数调用）的梯度计算（89）

使⽤⾃动求导的⼀个好处是，即使构建函数的计算图需要通过Python控制流（例如，条件、循环或任意函数调⽤），我们仍然可以计算得到的变量的梯度。在下⾯的代码中，while循环的迭代次数和if语句的结果都取决于输⼊a的值。

import torch


def f(a):
    b = a * 2
    while b.norm() < 1000:
        b = b * 2
    if b.sum() > 0:
        c = b
    else:
        c = 100 * b
    return c


def main():
    # 让我们计算梯度。
    a = torch.randn(size=(), requires_grad=True)
    print(a)    # tensor(0.2505, requires_grad=True)
    d = f(a)
    d.backward()
    # 我们现在可以分析上⾯定义的f函数。请注意，它在其输⼊a中是分段线性的。换⾔之，对于任何a，存在某
    # 个常量标量k，使得f(a)=k*a，其中k的值取决于输⼊a。因此，d/a允许我们验证梯度是否正确。
    print(a.grad == d / a)  # tensor(True)


if __name__ == '__main__':
    main()

2.5.5 小结（90）

• 深度学习框架可以⾃动计算导数。为了使⽤它，我们⾸先将梯度附加到想要对其计算偏导数的变量上。然后我们记录⽬标值的计算，执⾏它的反向传播函数，并访问得到的梯度。

2.5.6 练习（90）

1. 为什么计算⼆阶导数⽐⼀阶导数的开销要更⼤？
2. 在运⾏反向传播函数之后，⽴即再次运⾏它，看看会发⽣什么。
3. 在控制流的例⼦中，我们计算d关于a的导数，如果我们将变量a更改为随机向量或矩阵，会发⽣什么？此时，计算结果f(a)不再是标量。结果会发⽣什么？我们如何分析这个结果？
4. 重新设计⼀个求控制流梯度的例⼦。运⾏并分析结果。
   
   https://discuss.d2l.ai/t/topic/1759