一、引言

        人类现实生活中往往会遇到各种各样的抉择，而遇到每一个决策根据不同的情况，人脑会有不同的判断和选择。而随着事情不断深入，人们也不断随着不同的情况作出分析和判断。我们试图回顾人类做决策的过程和方法，发现其本质是一种树，于是顾名思义，机器学习中一种分类的方法---决策树被提出。

二、概念

决策树是一种机器学习的方法。决策树的生成算法有ID3, C4.5和C5.0等。决策树是一种树形结构，其中每个内部节点表示一个属性上的判断，每个分支代表一个判断结果的输出，最后每个叶节点代表一种分类结果。决策树是一种十分常用的分类方法，需要监管学习。监管学习就是给出一堆样本，每个样本都有一组属性和一个分类结果，也就是分类结果已知，那么通过学习这些样本得到一个决策树，这个决策树能够对新的数据给出正确的分类。    

三、决策树的基本内容

决策树是一种常见的机器学习算法，用于解决分类和回归问题。它模拟了人类在面临决策时的思考过程，并通过构建一个树状结构来表示决策规则。

决策树由节点（node）和边（edge）构成，其中节点分为内部节点和叶节点。内部节点表示对数据特征的测试，而叶节点表示最终的分类或回归结果。

决策树的构建过程通常从根节点开始，根据数据的特征进行划分，每个内部节点代表一个特征及其取值，而边则表示该特征的取值范围。根据内部节点的划分规则，数据将被分配到下一个子节点，直到达到叶节点为止。

构建决策树的关键是选择合适的特征进行划分。常见的划分准则有信息增益、基尼系数和误差率等。信息增益是根据信息论的概念计算的，它衡量了划分后的纯度提升程度；基尼系数则是度量数据集纯度的指标，用于选择最优的划分特征；而误差率则是用来选择错误最少的划分特征。

三、决策树的构建

（1）生成决策树

决策树的生成过程通过递归地进行特征选择、划分和子树生成来完成。下面是决策树生成的一般步骤：

1. 特征选择：从训练数据中选择一个最优的特征作为当前节点的划分特征。常见的特征选择准则有信息增益、基尼系数和误差率等。

2. 特征划分：根据选定的特征，将数据集划分成多个子集，每个子集对应特征的一个取值。这些子集将成为当前节点的子节点。

3. 递归生成子树：对每个子节点，重复步骤1和步骤2，直到满足终止条件。终止条件可以是达到预设的树的深度、数据集的样本数小于某个阈值或者所有样本都属于同一类别。

4. 构建叶节点：当达到终止条件时，生成叶节点并确定其分类标签。如果叶节点中的样本属于同一类别，则将该类别作为叶节点的分类标签；如果叶节点中的样本属于多个类别，则通常采用多数表决法来确定分类标签。

5. 递归返回：返回父节点，并继续选择下一个最优的特征，重复步骤1到步骤4，直到所有节点都生成。

决策树生成过程中的特征选择和特征划分是关键的步骤。特征选择准则的选择会影响树的性能和结构，不同的准则适用于不同的问题和数据集。特征划分的目标是将数据集按照特征的取值划分成不同的子集，使得子集内的样本尽可能属于同一类别，同时子集间的纯度差异尽可能大。

（2）剪枝

决策树剪枝是指通过一定的策略对生成的决策树进行减枝，从而避免过拟合现象并提高模型的泛化性能。决策树的剪枝过程通常分为预剪枝和后剪枝两个阶段。

1. 预剪枝：在决策树生成的过程中，对每个节点进行判断，如果某个节点没有提高模型泛化能力，则停止该节点的细分，并将该节点设为叶子节点。常见的预剪枝策略包括设定最大深度、节点样本数小于某个阈值或者信息增益小于某个阈值等。

2. 后剪枝：在决策树生成完毕之后，通过剪枝来优化决策树模型，剪枝的过程是自下而上的，从叶节点开始，逐渐向上剪枝。具体的剪枝策略有很多，常用的有悲观剪枝和代价复杂度剪枝。

• 悲观剪枝：悲观剪枝是指将子树替换为单个叶子节点的策略，即将子树中所有的叶子节点都替换为一个新的叶子节点，并重新计算模型的泛化误差。如果剪枝后的模型的泛化误差小于剪枝前的模型，则进行剪枝；否则不剪枝。

• 代价复杂度剪枝：代价复杂度剪枝是一种基于正则化的剪枝策略，它将剪枝的问题转换为模型选择的问题。具体来说，对每个子树计算一个代价函数，该函数由子树的训练误差和子树的模型复杂度两部分组成。模型复杂度可以用子树中的节点数或者叶子节点数来表示。然后从子树中选择一个代价最小的子树作为剪枝后的模型。

四、特征提取

决策树在每个节点上选择最优特征的目标是使得划分后的子集尽可能纯净，即同一类别的样本尽可能聚集在一起。常用的特征选择准则有信息增益、基尼系数和误差率等。

1. 信息增益（Information Gain）：信息增益是基于信息论的概念，用来衡量一个特征对于分类任务的贡献程度。信息增益越大，表示该特征能够更好地区分不同类别的样本。在每个节点上，计算每个特征的信息增益，选择信息增益最大的特征作为划分特征。

2. 基尼系数（Gini Index）：基尼系数是衡量节点纯度的指标，表示从一个数据集中随机选取两个样本，其类别标签不一致的概率。基尼系数越小，表示节点的纯度越高。在每个节点上，计算每个特征的基尼系数，选择基尼系数最小的特征作为划分特征。

3. 误差率（Error Rate）：误差率是指在当前节点上将样本分类到错误类别的概率。误差率越小，表示分类效果越好。在每个节点上，计算每个特征的误差率，选择误差率最小的特征作为划分特征。

选择特征的过程是通过计算每个特征的评估指标，然后选择具有最高评估指标的特征作为划分特征。这样就能够使得划分后的子集在分类任务上更加纯净，提升决策树模型的性能。需要注意的是，不同的特征选择准则偏好于不同类型的数据和问题。因此，在实际应用中，需要根据具体情况选择合适的特征选择准则来生成决策树。

五、决策树优势

1. 易于理解和解释：决策树的模型结构非常直观，类似于人类的决策过程，易于理解和解释。决策树可以生成可视化的树形结构，清晰地展示特征选择和决策路径，帮助人们理解模型的工作原理。

2. 可处理离散和连续特征：决策树可以处理离散和连续型特征，并不需要对数据进行特殊的预处理。对于离散特征，决策树可以根据特征取值对样本进行划分；对于连续特征，决策树可以通过设定阈值来划分样本。

3. 能够处理多分类问题：决策树可以直接应用于多分类问题，无需进行额外的修改或调整。它可以根据类别标签的分布情况，将样本划分到不同的叶子节点中，实现多个类别的分类。

4. 对异常值和缺失值具有鲁棒性：决策树在构建模型时并不依赖于全局数据分布，因此对于异常值和缺失值具有一定的鲁棒性。决策树可以通过划分其他样本来处理异常值，而对于缺失值，则可以根据其他特征的取值进行划分。

5. 可以用于特征选择：决策树在训练过程中会通过计算特征的重要性来选择最优的划分特征。因此，决策树可以作为一种特征选择的工具，帮助我们识别哪些特征对于分类或回归任务更加重要。

6. 适用于大规模数据集：决策树算法可以高效地处理大规模的数据集，因为它的训练和预测复杂度与样本数量和特征数量成线性关系。此外，由于决策树可以并行计算，因此可以通过并行化技术进一步提高训练速度。

六、决策树应用：网球预测

​

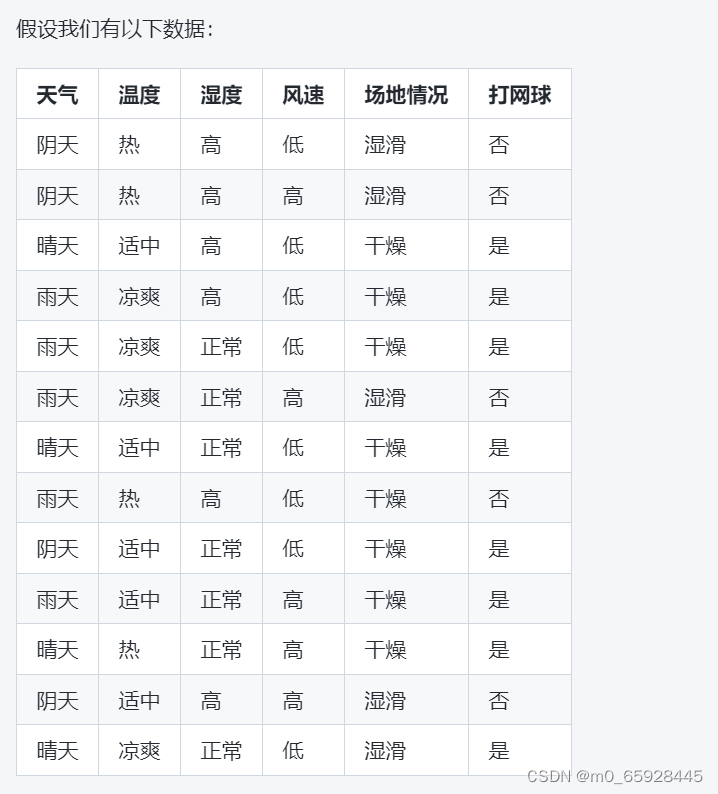
我们的目的是构建一个决策树，通过考虑天气、温度、湿度、风速和场地情况等因素来预测某一天是否适合打网球。首先，我们需要选择一个特征作为根节点。按照信息增益的准则，我们计算每个特征的信息增益，选择信息增益最大的特征作为根节点。在这个例子中，我们计算得到温度特征的信息增益最大，因此将温度作为根节点。接下来，我们需要对温度进行划分，在每个子节点上选择下一个最优划分特征。例如，如果当前节点的温度为“热”，那么我们可以选择湿度或风速作为下一个划分特征。在这里，我们选择湿度进行划分。如果当前节点的温度为“适中”或“凉爽”，那么我们选择风速进行划分。这样，我们就可以生成一个二叉决策树。

代码：

# 定义决策树类
class DecisionTree:
    def __init__(self, data, target):
        self.data = data
        self.target = target

    def entropy(self, data_column):
        # 计算信息熵
        values, counts = np.unique(data_column, return_counts=True)
        probabilities = counts / np.sum(counts)
        entropy = -np.sum(probabilities * np.log2(probabilities))
        return entropy

    def information_gain(self, data_column):
        # 计算信息增益
        total_entropy = self.entropy(self.target)
        values, counts = np.unique(data_column, return_counts=True)
        weighted_entropies = np.sum([(counts[i] / np.sum(counts)) * self.entropy(self.target[data_column == values[i]]) for i in range(len(values))])
        information_gain = total_entropy - weighted_entropies
        return information_gain

    def build_tree(self, data=None, target=None, features=None):
        if data is None:
            data = self.data
        if target is None:
            target = self.target
        if features is None:
            features = list(data.columns)

        # 如果所有实例都属于同一类别，则返回该类别
        if len(np.unique(target)) == 1:
            return target[0]

        # 如果特征列表为空，则返回数据中实例数最多的类别
        if len(features) == 0:
            return np.argmax(np.bincount(target))

        # 选择信息增益最大的特征作为节点
        gains = [self.information_gain(data[feature]) for feature in features]
        best_feature_index = np.argmax(gains)
        best_feature = features[best_feature_index]

        # 构建决策树
        tree = {best_feature: {}}
        unique_values = np.unique(data[best_feature])
        new_features = features[:best_feature_index] + features[best_feature_index+1:]

        for value in unique_values:
            sub_data = data[data[best_feature] == value]
            sub_target = target[data[best_feature] == value]
            tree[best_feature][value] = self.build_tree(sub_data, sub_target, new_features)

        return tree

    def predict(self, instance, tree):
        if not isinstance(tree, dict):
            return tree

        root = list(tree.keys())[0]
        subtree = tree[root]
        value = instance[root]

        if value not in subtree:
            return None

        return self.predict(instance, subtree[value])

# 示例代码
import pandas as pd
import numpy as np

# 创建数据集
data = {
    '天气': ['阴天', '阴天', '晴天', '雨天', '雨天', '雨天', '晴天', '雨天', '阴天', '雨天', '晴天', '阴天', '晴天'],
    '温度': ['热', '热', '适中', '凉爽', '凉爽', '凉爽', '适中', '热', '适中', '适中', '热', '适中', '凉爽'],
    '湿度': ['高', '高', '高', '高', '正常', '正常', '正常', '高', '正常', '正常', '正常', '高', '正常'],
    '风速': ['低', '高', '低', '低', '低', '高', '低', '低', '低', '高', '高', '高', '低'],
    '场地情况': ['湿滑', '湿滑', '干燥', '干燥', '干燥', '湿滑', '干燥', '干燥', '干燥', '干燥', '干燥', '湿滑', '湿滑'],
    '打网球': ['否', '否', '是', '是', '是', '否', '是', '否', '是', '是', '是', '否', '是']
}
df = pd.DataFrame(data)

# 提取特征和目标列
features = df.drop('打网球', axis=1)
target = df['打网球']

# 创建决策树实例并训练模型
dt = DecisionTree(features, target)
tree = dt.build_tree()

# 预测新样本
new_sample = {
    '天气': '晴天',
    '温度': '热',
    '湿度': '高',
    '风速': '低',
    '场地情况': '湿滑'
}
prediction = dt.predict(new_sample, tree)
print('预测结果:', prediction)

 ​

七、决策树的反思和局限

1. 过拟合问题：在构建复杂的决策树时，容易出现过拟合问题，即模型在训练集上表现很好，但在测试集上表现不佳。

2. 高度依赖数据质量：决策树算法的结果非常依赖于所使用的数据质量和特征选择方法。如果数据存在缺失值、异常值或噪声，决策树算法会受到影响，并且可能产生错误的预测结果。

3. 不稳定性问题：对于数据的微小变化，决策树的生成可能会产生较大的变化，导致结果不稳定。这是因为决策树的生成是基于基于启发式算法的贪心策略，而没有考虑全局优化问题。

4. 无法处理连续性变量：决策树算法通常只能处理分类变量，而对于连续型变量则需要将其离散化，这会造成一些信息的损失。

5. 容易受到样本不均衡的影响：决策树算法对于样本分布不均衡的情况容易出现问题，因为在决策树结构中，类别多的样本对分类起到主导作用，而对于类别少的样本，则很容易被忽略。

6. 可解释性问题：虽然决策树具有易于理解和可解释性的特点，但当决策树模型变得非常复杂时，人们可能无法理解决策树中每个节点的含义，从而降低了模型的可解释性、

7. 在使用决策树模型时，需要注意这些局限性和问题，并采取相应的方法来解决或减轻这些问题的影响。例如，在数据预处理过程中，可以采用缺失值处理、异常值检测和噪声过滤方法来提高数据质量；在模型训练过程中，可以使用剪枝和交叉验证等技术来避免过拟合和提高模型泛化能力。