一、数据降维的应用

(1)数据降维的第一个应用：数据压缩

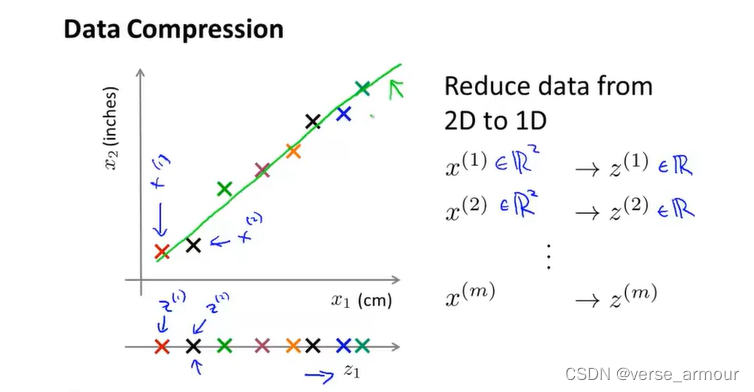
将二维的数据压缩到一维上去。可以加速学习算法。

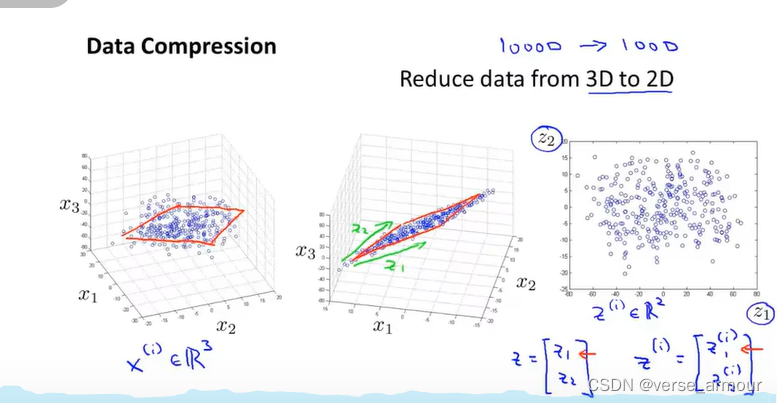
将三维空间中的点投影到一个二维的平面上，这样只需要两个数据就能表示一个点

(2)数据降维的第二个应用：可视化数据

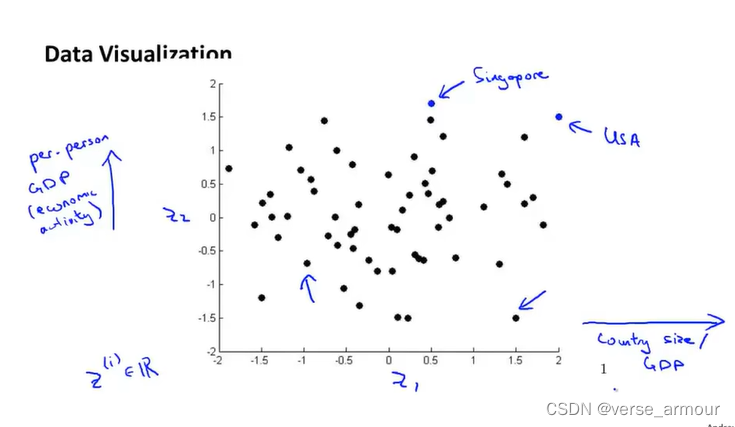
将高维数据降到2维可以用于数据的可视化

二、数据降维算法——主成分分析（PCA）

（1）2D->1D

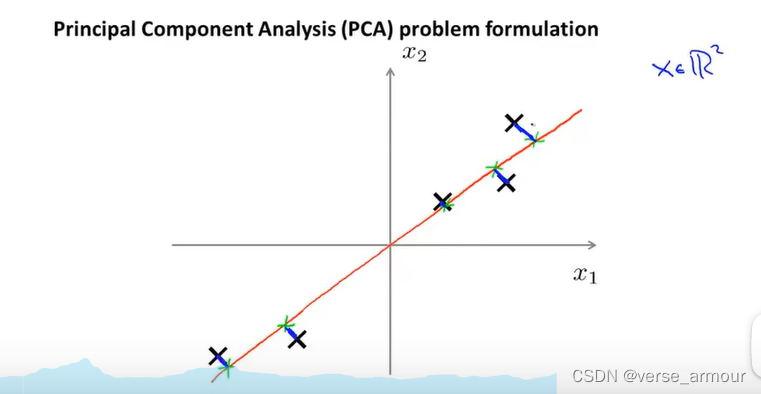
在PCA之前，要先进行均值归一化、和特征规范化，使得特征向量$x_1$和$x_2$其均值为0，并且数值在可比较的范围之内。

PCA会找一个低维平面（这个例子是一个直线），然后将数据投影在上面，使投影误差（投影长度平方）最小。

(2)3D->2D

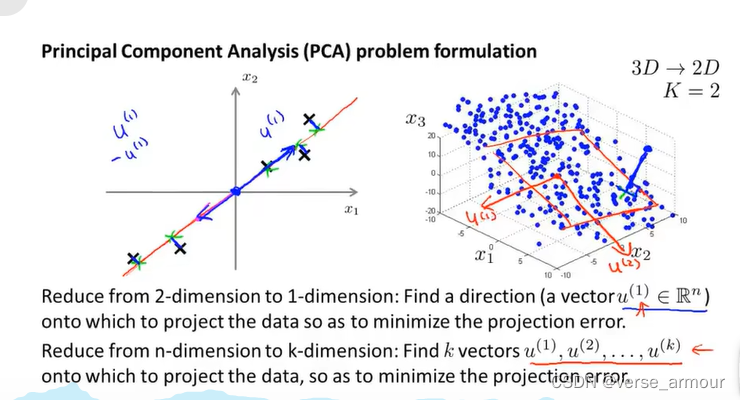
更普遍的情况：我们有N维的数据，我们想将其降维到K维，在这种情况下，我们不只想找个单个向量，来对数据进行投影；而是想寻找K个方向，来对数据进行投影，我们可以用K个向量来定义平面中这些点的位置，来最小化平方投影误差。

（3）线性回归和PCA对比

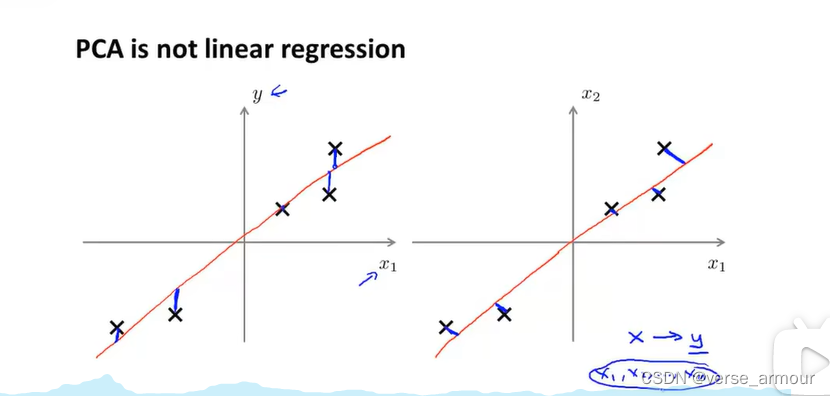
线性回归	PCA
竖直距离	垂直距离
用$x$来预测$y$值	没有这种区别对待的概念，$x_1$,$x_2$,…,$x_n$是同等地位

三、PCA算法实现

（1）前置知识

奇异值分解（SVD）：奇异值分解能够用于任意m*n矩阵，而特征分解只能适用于特定类型的方阵，故奇异值分解的适用范围更广。

协方差矩阵总是满足正定矩阵的性质

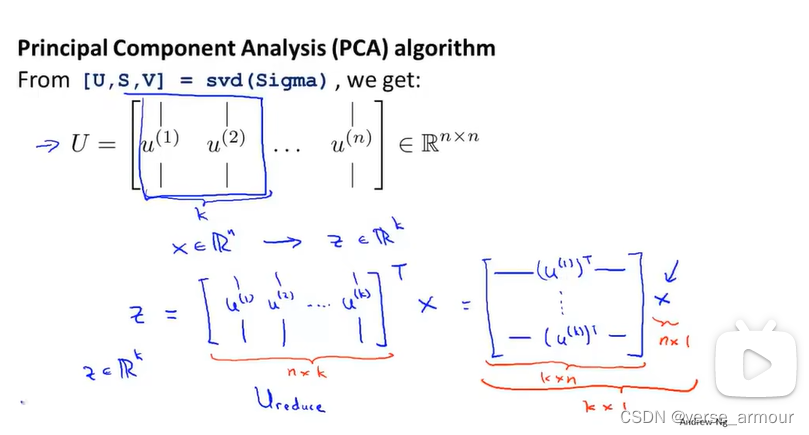
（2）算法实现

协方差矩阵总是满足正定矩阵的性质

如果我们想把数据从n维降到K维，我们只需要矩阵U的前k列向量。

这里可以尝试去理解一下在矩阵中，特征向量和特征值的几何意义。这里的奇异值类似方阵中的特征值，是表示特征向量重要程度的一个东西。

总结：

• 进行均值归一化之后，为确保每一个特征都是均值为0的任选特征缩放

• 计算载体矩阵$\Sigma$:向量化表示
  

• 奇异值分解
  

四、主成分数量选择

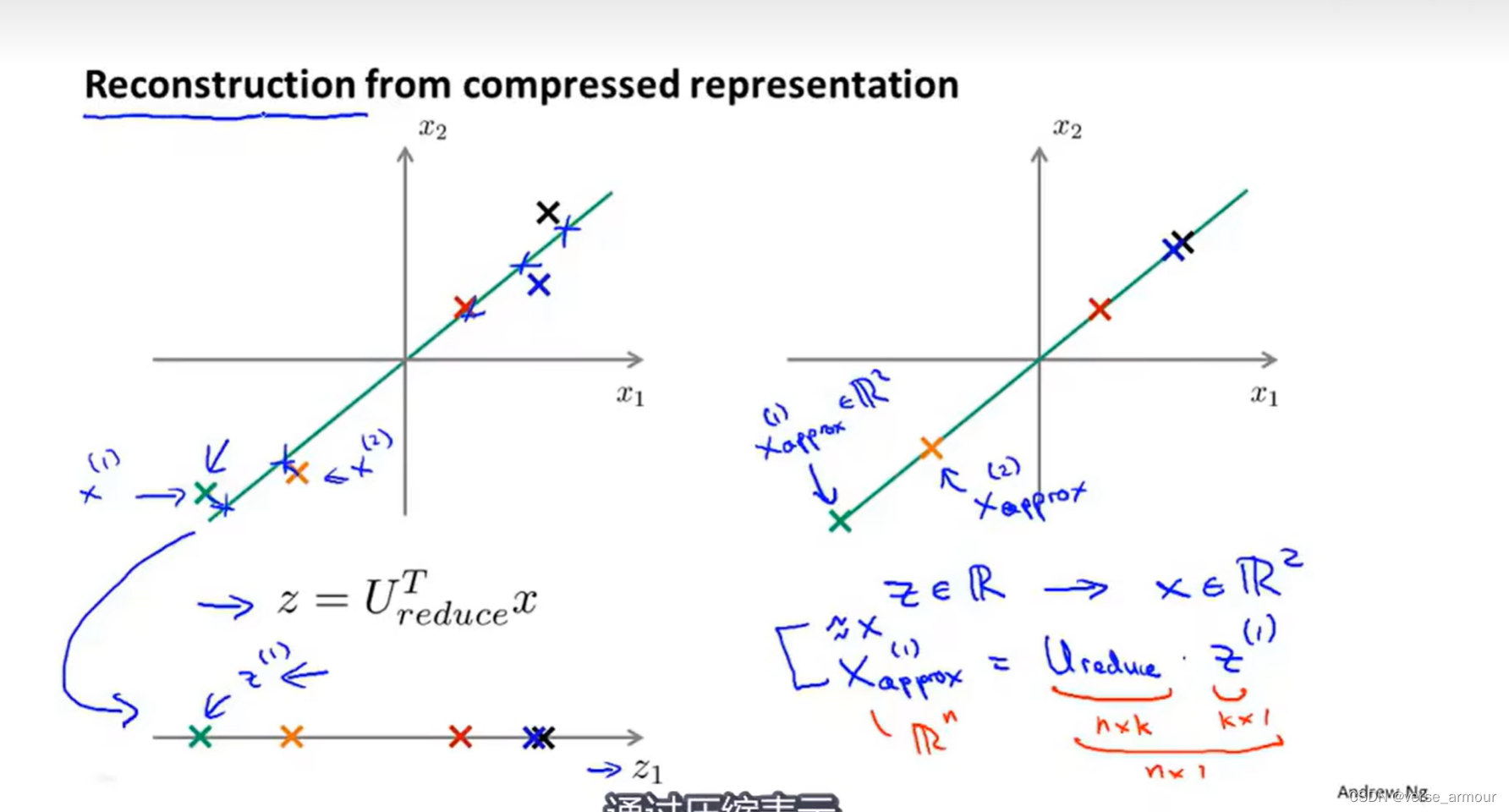
五、压缩重现

六、应用PCA的建议

对于高维数据（比如图像处理），运行学习算法时将会变得非常慢，如果要使用10000维的特征向量进行logistic回归，或者输入神经网络或者支持向量机，因为数据量太大，将会使我们的学习算法运行得非常慢。PCA可以降低数据维度，加速我们的监督学习算法。

• 检查已经被标记的训练集，并且抽取输入向量$x_1$,$x_2$,…,$x_m$,得到一个没有标签的数据集。（m表示样本个数，在这个图像处理的例子中，m指训练集中图像的个数，$R^{10000}$中的10000指的是每一个样本图像的像素点个数）。

• 使用PCA得到原始数据的低维表示
  

• 此时可以用更低维的特征向量来作为监督学习算法的输入

注意：$x$到$z$的映射只能通过在训练集上运行PCA来定义

PCA学习的这个映射所做的，就是计算一系列参数进行特征缩放和均值归一化还计算$U_{reduced}$，所有的这些参数都只在训练集上运行PCA得到，而不是在交叉验证集或测试集。得到参数后，可以将所的参数应用在交叉验证集和测试集，将x都映射成z。（PCA就是在训练前把train，validation，test都映射成z）

我们减少了数据的维度，同时又保留大部分的方差，几乎不影响性能。

如何选择K：

为了计算出K我们通常会计算出方差保留百分比，通常需要保留99%的方差

可视化：

K=2或3

用PCA降维减少特征数量去避免过拟合并不合适

我们应该用正则化项来避免过拟合

写在最后：

一般情况下，如果不是学习算法运行的速度太慢、需要的内存或硬盘空间太大，我们会选择直接在原始数据上训练而非先用PCA降维。PCA会丢失有意义的数据信息。