深度学习概述

什么是深度学习？

深度学习是一种基于人工神经网络的 机器学习方法，它通过模拟人脑神经元之间的连接和工作方式，进行数据的自动特征提取和抽象化处理。深度学习的本质在于 层次化学习，从低层次的特征到高层次的特征逐步构建，从而完成复杂任务，如图像分类、语音识别和自然语言处理等。

机器学习是实现人工智能的一种途径，深度学习是机器学习的子集，区别如下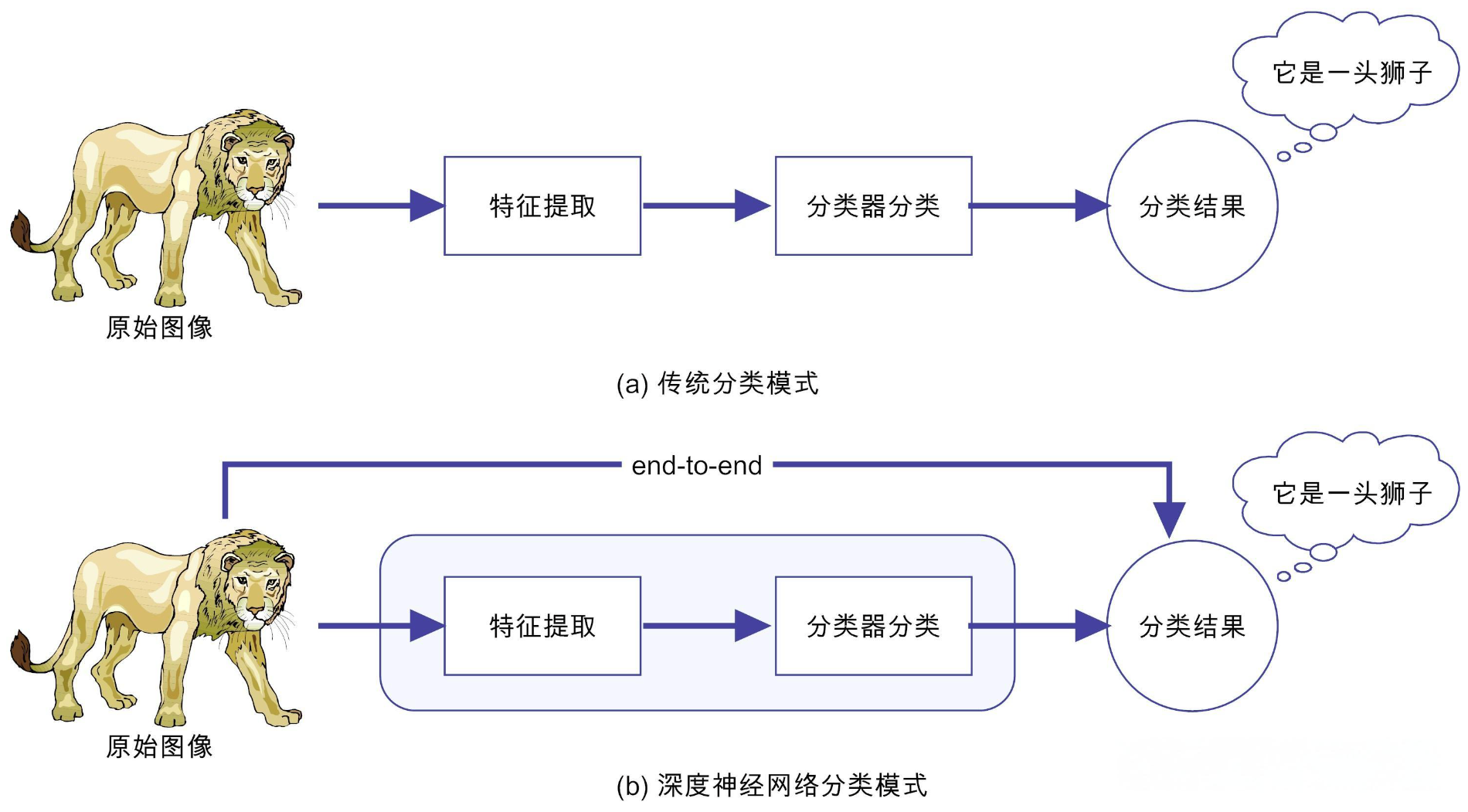
传统机器学习算法依赖人工设计特征、提取特征，而深度学习依赖算法自动提取特征。深度学习模仿人类大脑的运行方式，从大量数据中学习特征，这也是深度学习被看做黑盒子、可解释性差的原因。

​ 随着算力的提升，深度学习可以处理图像，文本，音频，视频等各种内容，主要应用领域有：

1. 图像处理：分类、目标检测、图像分割（语义分割）
2. 自然语言处理：LLM、NLP、Transformer
3. 语音识别：对话机器人、智能客服（语音+NLP）
4. 自动驾驶：语义分割（行人、车辆、实线等）
5. LLM：大Large语言Language模型Model
6. 机器人：非常火的行业

有了大模型的加持，AI+各行各业。

为什么要用深度学习？

深度学习的 优势 在于它能够自动从 原始数据 中学习特征，而无需人工设计特征工程。传统机器学习算法依赖于手动特征提取，而深度学习通过构建多层神经网络，能够 自适应地 从数据中提取最优特征，极大提高了处理复杂问题的能力。

深度学习的发展历史

深度学习的核心技术源自 神经网络，但其在多个阶段经历了波动。

1. 1950s-1980s：早期的神经网络模型（如感知机）首次提出，但由于计算能力限制和数据不足，发展停滞。
2. 1990s：随着反向传播算法的提出，神经网络逐步得到了应用，尤其是在图像和语音的处理上。
3. 2000s：深度学习真正迎来了复兴。通过更深层的神经网络结构，以及更强大的计算能力（GPU的使用），深度学习开始展现出巨大的潜力。
4. 2010s：深度学习在 计算机视觉、语音识别 和 自然语言处理 等领域的成功应用，推动了人工智能技术的快速发展，成为主流技术。

为什么深度学习能够成功？

• 计算能力的提升：通过GPU加速计算，深度神经网络可以处理大规模数据。
• 大数据的支持：海量数据的获取和处理，使得深度学习能够发挥其强大的特征提取能力。
• 改进的算法：如卷积神经网络（CNN）、循环神经网络（RNN）、生成对抗网络（GAN）等的提出，使得深度学习能够解决更复杂的问题。

深度学习的优势

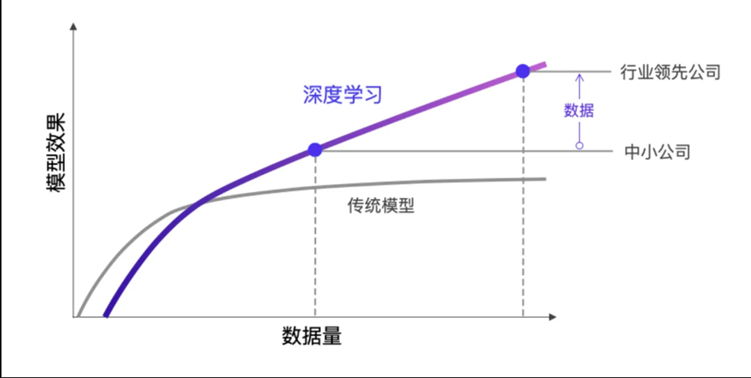
1. 自动特征提取：深度学习不依赖于人工提取特征，能够自动从原始数据中学习有效特征。
2. 强大的建模能力：能够处理复杂的非线性关系，适用于图像、语音、文本等多种类型的数据。
3. 端到端学习：深度学习可以通过端到端的训练方式，直接从输入数据到输出结果，减少了中间步骤。
4. 迁移学习：预训练的深度网络能够在不同任务中迁移，节省训练时间和计算资源。

---

神经网络

感知神经网络

感知机（Perceptron）是最简单的人工神经网络，它是 单层神经网络 的基础。感知机由 输入层 和 输出层 组成，能用于处理线性可分的问题。

为什么要有感知神经网络？

感知机能够通过 加权求和 和 激活函数 计算输出，使得它能在某些任务中执行分类任务。虽然它只能处理 线性可分问题，但它为后来的 多层神经网络（如 前馈神经网络）奠定了基础。

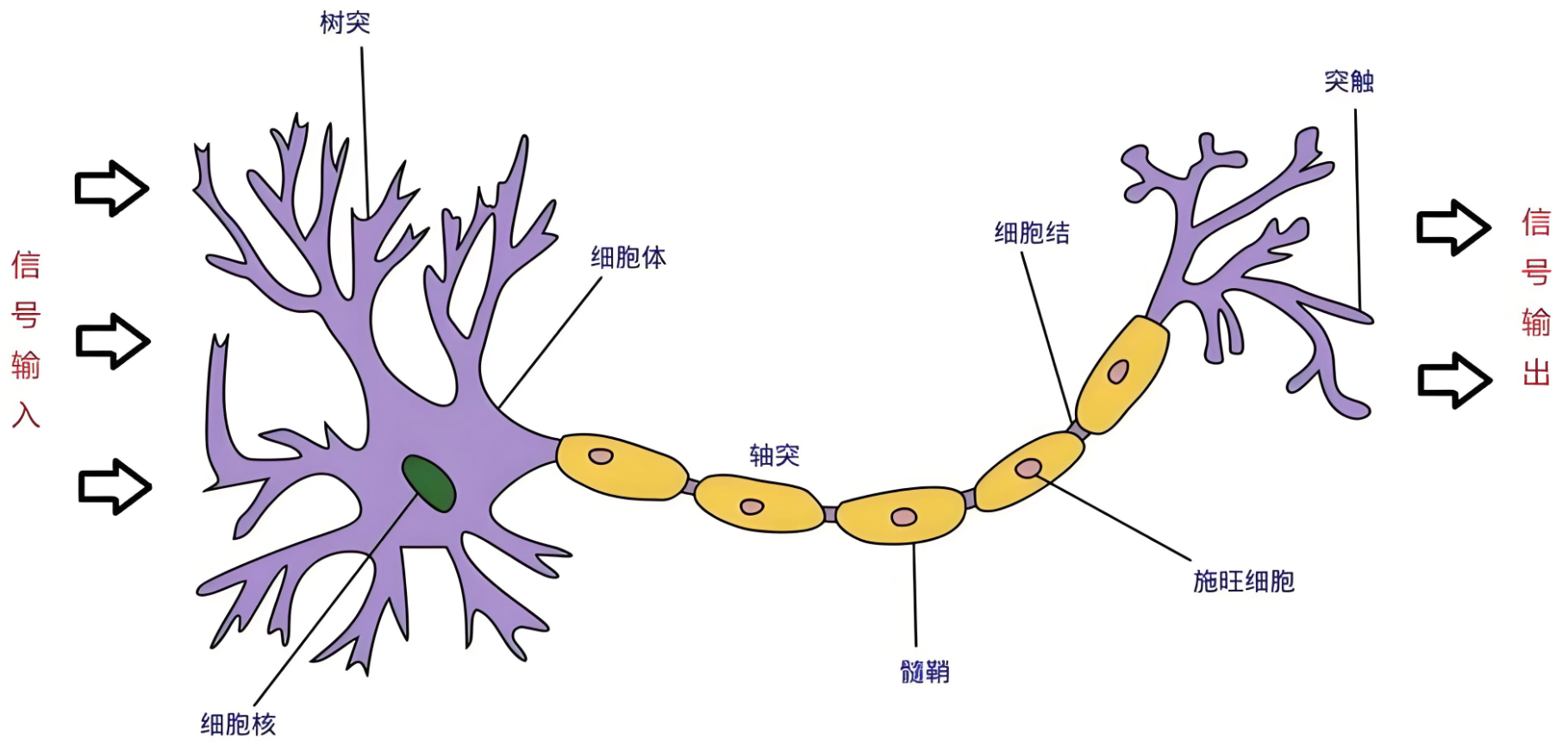
人工神经元

构建人工神经元

人工神经元的结构模拟了生物神经元的基本功能，主要由三个部分组成：

1. 输入（Input）：神经元接收来自其他神经元或外部环境的信息。
2. 加权求和（Weighted Sum）：每个输入信号都会乘以一个权重，表示该输入的重要程度。
3. 激活函数（Activation Function）：对加权求和的结果进行非线性变换，决定神经元是否激活。

数学表示

人工神经元的计算过程可以用以下公式表示：

$$y=f\left(\sum _{i=1}^n{w}_i{x}_i+b\right)$$

其中：

• $x_i$ 是输入信号，
• $w_i$ 是对应的权重，
• $b$ 是偏置项，
• $f()$ 是激活函数，常见的激活函数包括 Sigmoid、ReLU 和 Tanh。

为什么要有激活函数？

激活函数引入了 非线性，使得神经网络能够 表示复杂的非线性关系。如果没有激活函数，即使多层堆叠，神经网络也只能表示 线性模型。

深入神经网络

基本结构

神经网络由多个层组成，包括：

1. 输入层：接收外部数据的输入。(神经网络的第一层，不进行计算)
2. 隐藏层：负责学习数据的特征表示。深度学习中的“深度”就是指有多个隐藏层。（进行特征提取和转换，每个隐藏层都有多个神经元）
3. 输出层：根据学习到的特征做出预测或分类。

网络构建

神经网络的 构建 是通过 多层感知机（MLP） 或更复杂的网络结构来实现。每一层的输出都被当作下一层的输入，逐步提取数据的特征。深度神经网络的优势在于通过 层次化学习 来从数据中学习更加抽象和复杂的特征。

全连接神经网络

全连接神经网络（Fully Connected Neural Network, FCN）是一种 基础的神经网络结构，每一层的每个神经元都与前一层的所有神经元相连。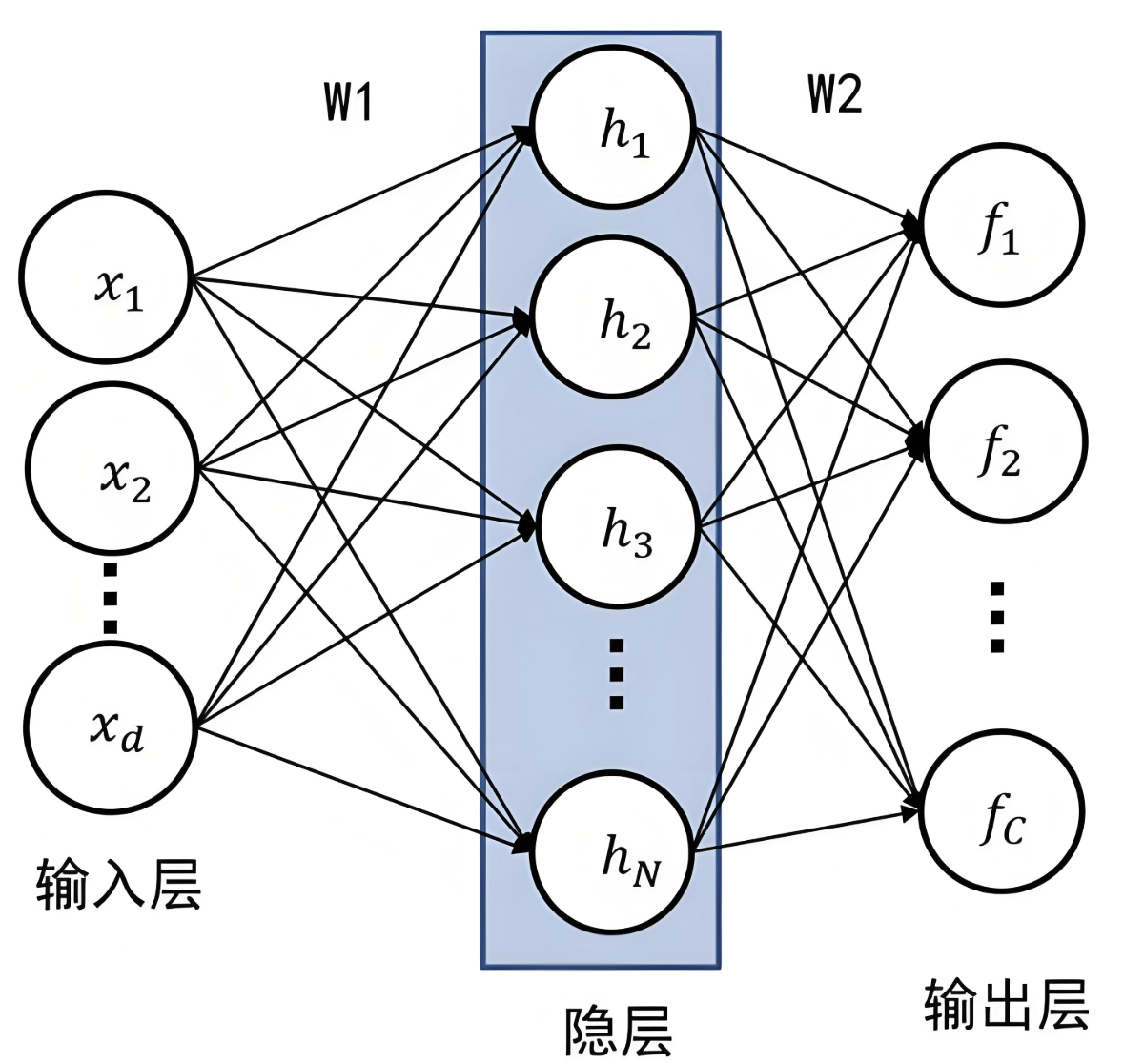


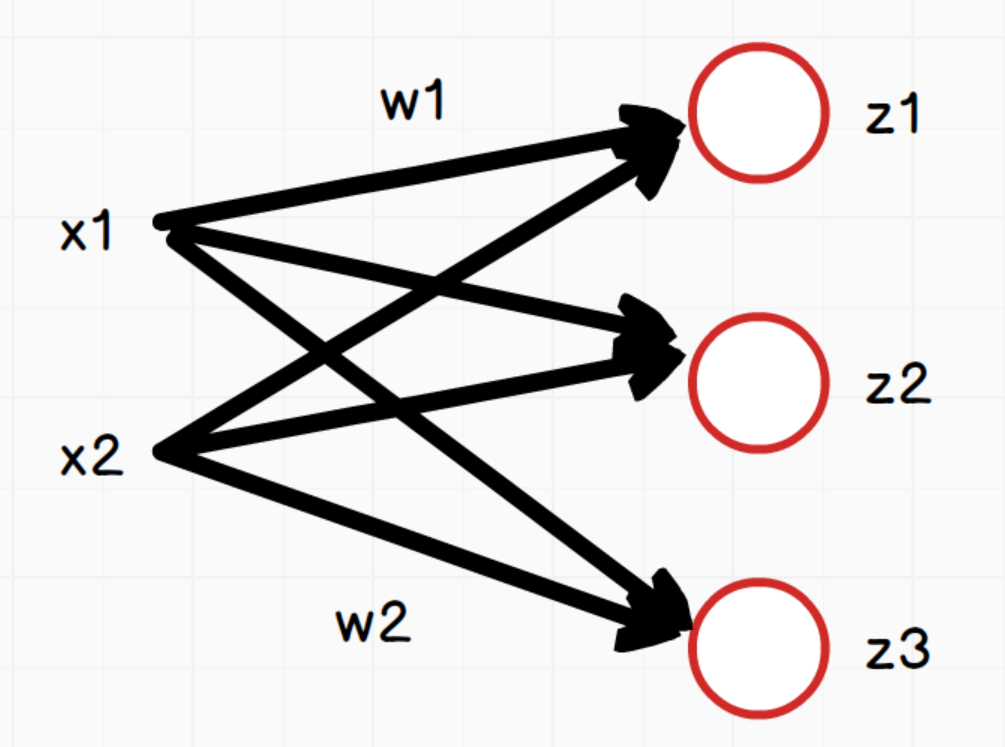
如上图，网络中每个神经元：
$$\begin{gathered} z_1=x_1\ast w_1+x_2\ast w_2+b_1 \\ {z}_2=x_1\ast w_1+x_2\ast w_2+b_2 \\ {z}_3=x_1\ast w_1+x_2\ast w_2+b_3 \end{gathered}$$
说明：三个等式中的w1和w2在这里只是为了方便表示对应x1和x2的权重，实际三个等式中的w值是不同的。

向量x为：$[x_1,x_2]$

向量w：$$\left(\begin{array}{c}{w}_1,w_2\\ w_1,w_2\\ w_1,w_2\end{array}\right)$$，其形状为（3，2），3是神经元节点个数，2是向量x的个数

向量z：$$[z_1,z_2,z_3]$$

向量b：$[b_1,b_2,b_3]$

所以用向量表示为：
$$z=\left(\begin{array}{c}{z}_1,z_2,z_3\end{array}\right)=\left(\begin{array}{c}{x}_1,x_2\end{array}\right)\left(\begin{array}{c}{w}_1,w_1,w_1\\ w_2,w_2,w_2\end{array}\right)+\left(\begin{array}{c}{b}_1,b_2,b_3\end{array}\right)=\left(\begin{array}{c}{x}_1,x_2\end{array}\right){\left(\begin{array}{c}{w}_1,w_2\\ w_1,w_2\\ w_1,w_2\end{array}\right)}^T+\left(\begin{array}{c}{b}_1,b_2,b_3\end{array}\right)=x{w}^T+b$$

• x是输入数据，形状为 (batch_size, in_features)。
• W是权重矩阵，形状为 (out_features, in_features)。
• b是偏置项，形状为 (out_features,)。
• z是输出数据，形状为 (batch_size, out_features)。

特点

1. 高灵活性：能够处理各种各样的数据，尤其是 非线性 数据。
2. 计算密集：每层神经元都与上一层神经元连接，这导致了大量的计算。
3. 适用于小规模数据：对于小规模的特征数据，FCN能取得不错的表现。

计算步骤

在全连接神经网络中，数据通过每一层的神经元进行加权求和，然后通过 激活函数 进行处理。最终，在输出层得到模型的预测结果。具体步骤如下：

1. 加权求和：每个神经元计算输入和权重的加权和。
2. 激活：通过激活函数对加权和进行非线性转换。
3. 输出：将最后一层的结果作为预测输出。

基本组件认知

• 权重（Weights）：连接各个神经元的参数，决定了网络如何从输入到输出。
• 偏置（Bias）：提供了额外的调整量，帮助网络适应数据。
• 激活函数（Activation Function）：引入非线性，使网络能够学习复杂模式。
• 这里推荐呢阅读官方文档：Pytorch
  线性层组件

nn.Linear是 PyTorch 中的一个非常重要的模块，用于实现全连接层（也称为线性层）。它是神经网络中常用的一种层类型，主要用于将输入数据通过线性变换映射到输出空间。

torch.nn.Linear(in_features, out_features, bias=True)

参数说明：

in_features：

• 输入特征的数量（即输入数据的维度）。
• 例如，如果输入是一个长度为 100 的向量，则 in_features=100。

out_features：

• 输出特征的数量（即输出数据的维度）。
• 例如，如果希望输出是一个长度为 50 的向量，则 out_features=50。

bias：

• 是否使用偏置项（默认值为 True）。
• 如果设置为 False，则不会学习偏置项。

示例：构建3层全连接神经网络：在__init__方法中定义网络结构，在forward定义前向传播

import torch
from torch import nn
# 定义全连接神经网络模型
class MyFcnn(nn.Module):
    def __init__(self, input_size,out_size):
        # 父类初始化
        super(MyFcnn, self).__init__()
        # 定义线性层1
        self.fc1 = nn.Linear(input_size, 64)

        # 定义线性层2，输入要和第一层的输出一致
        self.fc2 = nn.Linear(64, 32)

        # 定义线性层3，输入要和第二层的输出一致
        self.fc3 = nn.Linear(32, out_size)

    def forward(self, x):
        x = self.fc1(x)
        x = self.fc2(x)
        x = self.fc3(x)
        return x

input_size = 32
out_size = 1
model = MyFcnn(input_size,out_size)
print(model)

如果模型中线性层按顺序叠加，也可以使用nn.Sequential构建模型。nn.Sequential 是一个顺序容器，内置了自动的前向传播逻辑，它会自动将输入数据依次传递给其中的每一层，并执行前向传播，不需要显式定义 forward() 方法。

import torch
from torch import nn

input_size = 32
# 定义全连接神经网络模型
model = nn.Sequential(
    nn.Linear(input_size, 64),
    nn.Linear(64, 32),
    nn.Linear(32, 1)
)
print(model)

激活函数组件

激活函数的作用是在隐藏层引入非线性，使得神经网络能够学习和表示复杂的函数关系，使网络具备非线性能力，增强其表达能力。

常见激活函数：

sigmoid函数：

import torch.nn.functional as F
sigmoid = F.sigmoid()

tanh函数：

tanh = F.tanh()

ReLU函数：

import torch.nn as nn
relu = nn.ReLU()

LeakyReLU函数：

leaky_relu = nn.LeakyReLU(negative_slope=0.01)

softmax函数：

softmax = F.softmax

损失函数组件

损失函数的主要作用是量化模型预测值（y^）与真实值（y）之间的差异。通常，损失函数的值越小，表示模型的预测越接近真实值。训练过程中，通过优化算法（如梯度下降）最小化损失函数，从而调整模型的参数。

PyTorch已内置多种损失函数，在构建神经网络时随用随取！

文档：https://pytorch.org/docs/stable/nn.html#loss-functions

根据任务类型（如回归、分类等），损失函数可以分为以下几类：

回归任务的损失函数：

1.均方误差损失（MSE Loss）

• 函数: torch.nn.MSELoss

  import torch.nn as nn
  loss_fn = nn.MSELoss()
  

2.L1 损失（L1 Loss）

也叫做MAE（Mean Absolute Error，平均绝对误差）

• 函数: torch.nn.L1Loss

  import torch.nn as nn
  loss_fn = nn.L1Loss()
  

分类任务的损失函数：

1.交叉熵损失（Cross-Entropy Loss）

• 函数: torch.nn.CrossEntropyLoss

  cross_entropy_loss = nn.CrossEntropyLoss()
  

• 参数：reduction：mean-平均值，sum-总和

• 适用场景: 用于多分类任务。

2.二元交叉熵损失（Binary Cross-Entropy Loss）

• 函数: torch.nn.BCELoss 或 torch.nn.BCEWithLogitsLoss

  bce_loss = nn.BCELoss()
  bce_with_logits_loss = nn.BCEWithLogitsLoss()
  

• 适用场景: 用于二分类任务。

• 特点: BCEWithLogitsLoss 更稳定，因为它结合了 Sigmoid 激活函数和 BCE 损失。

• 注意：使用 nn.BCELoss 时，需要确保预测值经过 sigmoid 函数处理。如果预测值是 logits（即未经 sigmoid 处理的预测值），可以使用 nn.BCEWithLogitsLoss，它内部会自动应用 sigmoid 函数。

优化器

官方文档：https://pytorch.org/docs/stable/optim.html

在PyTorch中，优化器（Optimizer）是用于更新模型参数以最小化损失函数的核心工具。

PyTorch 在 torch.optim 模块中提供了多种优化器，常用的包括：

• SGD（随机梯度下降）
• Adagrad（自适应梯度）
• RMSprop（均方根传播）
• Adam（自适应矩估计）

核心方法有：

zero_grad()：清空模型参数的梯度（将梯度置零）。必须在loss.backward()之前调用zero_grad()，避免梯度累积。

step()：参数更新；是优化器的核心方法，用于根据计算得到的梯度更新模型参数。优化器会根据梯度和学习率等参数，调整模型的权重和偏置。

以SGD(随机梯度下降)优化器为例：

import torch
import torch.nn as nn
import torch.optim as optim

# 优化方法SGD的学习
def test003():
    model = nn.Linear(20, 60)
    criterion = nn.MSELoss()
    # 优化器：更新模型参数
    optimizer = optim.SGD(model.parameters(), lr=0.01)
    input = torch.randn(128, 20)
    output = model(input)
    # 计算损失及反向传播
    loss = criterion(output, torch.randn(128, 60))
    # 梯度清零
    optimizer.zero_grad()
    # 反向传播
    loss.backward()
    # 更新模型参数
    optimizer.step()
    
    print(loss.item())


if __name__ == "__main__":
    test003()

• optim.SGD(）：优化器方法；是 PyTorch 提供的随机梯度下降（Stochastic Gradient Descent, SGD）优化器。
• model.parameters()：模型参数获取；是一个生成器，用于获取模型中所有可训练的参数（权重和偏置）。

注意：这里只是组件认识和用法演示，没有具体的模型训练功能实现

---

总结

深度学习已成为现代人工智能领域的核心技术，特别是在图像处理、自然语言处理和语音识别等任务中表现出色。其核心优势在于能够自动从数据中提取特征，而无需人工干预，这使得深度学习能够处理各种复杂任务，展现了强大的建模能力。

神经网络作为深度学习的基础，通过模拟人类神经元之间的连接与工作方式，逐步从简单的感知机发展为复杂的多层神经网络。激活函数的引入，使得神经网络能够表示复杂的非线性关系，进而解决更具挑战性的问题。

随着计算能力的提升和大数据的支持，深度学习不断突破传统机器学习的局限，应用场景也不断扩大。从全连接神经网络到卷积神经网络（CNN）、循环神经网络（RNN）等多种网络架构的发展，深度学习正在不断优化和发展，成为各行业转型和创新的重要驱动力。

未来，随着大模型的出现和不断发展的技术，深度学习将继续推动人工智能的进步，影响着我们生活的各个方面，包括自动驾驶、医疗诊断、金融风控等领域。