深度学习之 2 数学基础
深度学习之 2 数学基础
·
本文是接着上一篇深度学习之 1 机器学习基础_水w的博客-CSDN博客
目录
数学基础
1、线性代数
(1)基本概念
• 标量(scalar) :一个标量就是一个单独的数,只有大小,没有方向• 向量(vector) :一个向量是由一组实数组成的有序数组,有大小,有方向• 矩阵(matrix) :矩阵是一个二维数组,其中的每一个元素被两个索引(而非一个)所确定• 张量(tensor) :在某些情况下,需要使用坐标超过两维的数组
(2)矩阵运算
• 转置• 矩阵加法• 矩阵乘法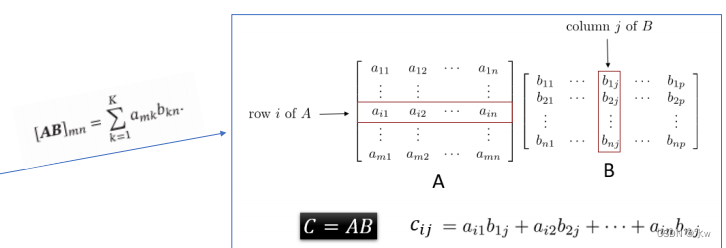 • 逆矩阵运算
• 逆矩阵运算
(3)范数:一个表示向量长度的函数
矩阵的范数,常用的 ℓp 范数定义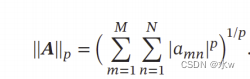 矩阵的 𝒍 𝟐范数又叫F范数,是向量的𝒍𝟐范数的推广
矩阵的 𝒍 𝟐范数又叫F范数,是向量的𝒍𝟐范数的推广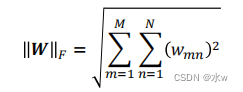

2、微积分
(1)导数:曲线的斜率,反应曲线变化的快慢
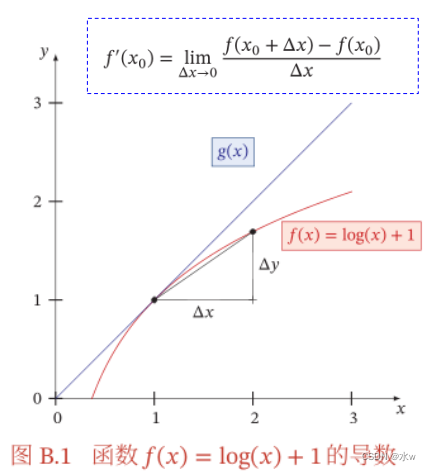
- 常见函数的导数:
- 高阶导数:导数的继续求导
- 偏导数:关于其中一个变量的导数, 而保持其他变量固定
- 方向导数:对某一方向求导得到的导数
(2)泰勒公式
一个函数 f ( x ) 在已知某一点的各阶导数值的情况之下, 可以用这些导数值做系数构建一个多项式来近似函数在这一点的邻域中的值。
(3)方向导数与梯度 :梯度向量是方向导数最大的方向
(4)矩阵微分
多元微积分的一种表达方式, 即使用矩阵和向量来表示因变量每个成分关于自变量每个成分的偏导数。
- 分母布局:
(5)微分链式法则
- 标量的微分链式法则:
- 向量的微分链式法则:
3、概率和统计
(1)概率
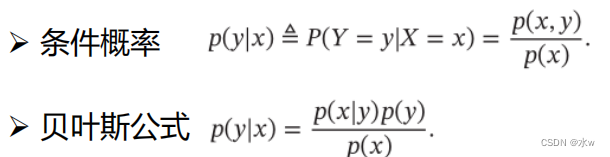
(2)常见概率分布
- 离散随机变量的概率分布有: 伯努利分布、二项分布
- 连续随机变量的概率分布有: 均匀分布、正态分布
(3)Jensen不等式:期望的函数小于等于函数的期望

(4)大数定理、随机过程、信息熵 …
更多推荐
 已为社区贡献22条内容
已为社区贡献22条内容


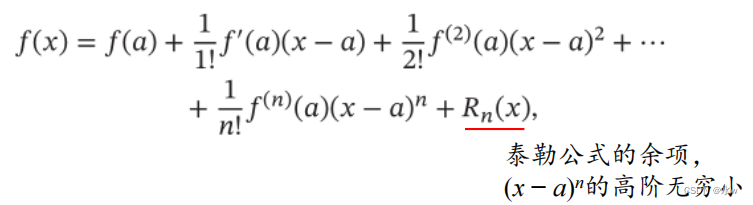


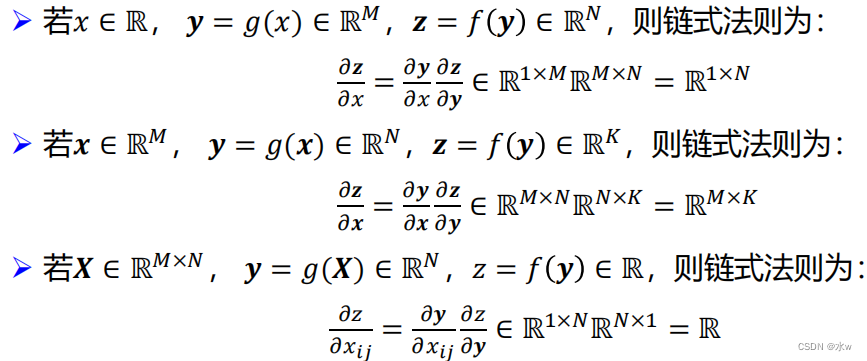








所有评论(0)