吴恩达机器学习-5-神经网络学习Neural Networks Learning
公众号:尤而小屋作者:Peter编辑:Peter吴恩达机器学习-5-神经网络学习Neural Networks Learning本文是在上节神经网络的基础上,做了进一步的阐述,内容包含:神经网络代价函数反向传播法及解释梯度检验神经网络的小结神经网络代价函数参数解释对几个参数的标记方法进行说明解释:mmm:训练样本个数x,yx,yx,y:输入和输出信号LLL:代表神经网络层数SI{S}_{I}SI
公众号:尤而小屋
作者:Peter
编辑:Peter
吴恩达机器学习-5-神经网络学习Neural Networks Learning
本文是在上节神经网络的基础上,做了进一步的阐述,内容包含:
- 神经网络代价函数
- 反向传播法及解释
- 梯度检验
- 神经网络的小结
神经网络代价函数
参数解释
对几个参数的标记方法进行说明解释:
- mmm:训练样本个数
- x,yx,yx,y:输入和输出信号
- LLL:代表神经网络层数
- SI{S}_{I}SI:每层的神经元个数
- Sl{S}_{l}Sl:表示输出神经元个数
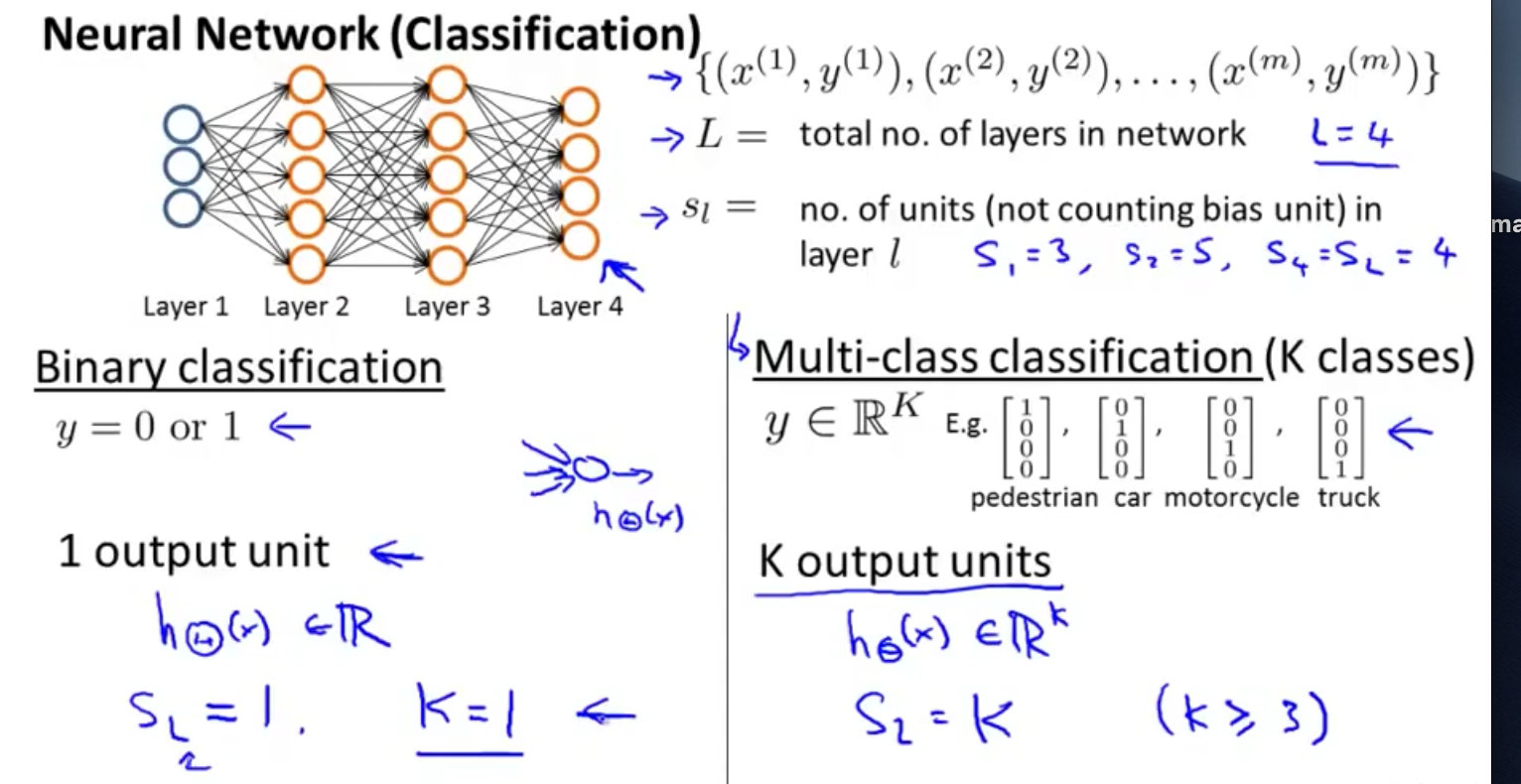
分类讨论
主要是两类:二分类和多类分类
二类分类:SL=0,y=0/1S_L=0,y=0/1SL=0,y=0/1;输出是一个实数
KKK类分类:SL=k,yi=1S_L=k,y_i=1SL=k,yi=1表示分到第iii类的情况。输出是一个多维向量
代价函数
逻辑斯蒂回归(LR)中的代价函数:
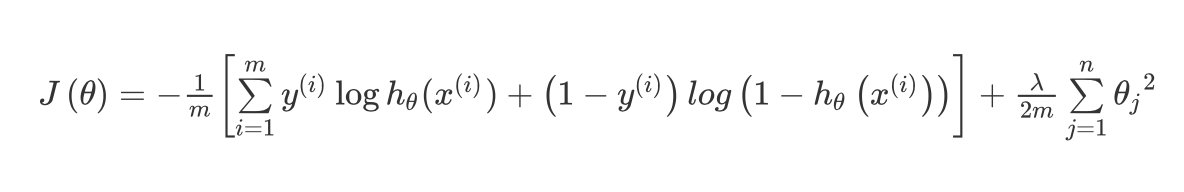
KaTeX parse error: Expected group after '_' at position 46: …1}{m}\left[\sum_̲\limits{i=1}^{m…
在逻辑斯蒂回归中,只有一个输出变量称之为标量scalar。
但是在神经网络中会有多个输出变量,hθ(x)h_\theta(x)hθ(x)是一个KKK维的向量。
假设第iii个输出函数:
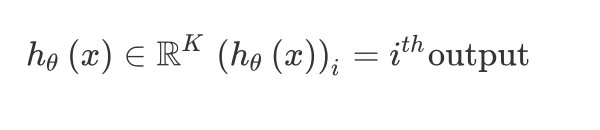
\newcommand{\subk}[1]{ #1_k } hθ(x)∈RKh_\theta\left(x\right)\in \mathbb{R}^{K}hθ(x)∈RK (hθ(x))i=ithoutput{\left({h_\theta}\left(x\right)\right)}_{i}={i}^{th} \text{output}(hθ(x))i=ithoutput
代价函数JJJ表示为:
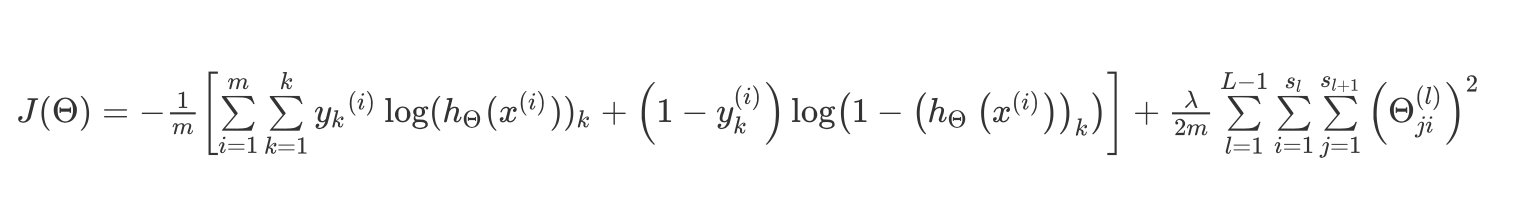
KaTeX parse error: Undefined control sequence: \subk at position 94: …_k}^{(i)} \log \̲s̲u̲b̲k̲{(h_\Theta(x^{(…
解释说明:
- 期望通过代价函数来观察算法预测的结果和真实情况的误差
- 每行特征会有KKK个预测,利用循环对每行进行预测
- 在KKK个预测中选择出可能性最高的那个,将其和实际的数据yyy进行比较
- 正则化项是排除了每个偏置θ0\theta_0θ0之后,每层θ\thetaθ矩阵的求和
- 参数jjj(由sl+1s_l+1sl+1层的激活单元数决定)循环所有的行,iii(由sls_lsl层的激活单元数决定)循环所有的列
反向传播法Backpropagation Algorithm

为了计算神经网络中代价函数的偏导数∂J(Θ)∂Θij(l)\frac{\partial J(\Theta)}{\partial \Theta_{ij^{(l)}}}∂Θij(l)∂J(Θ),需要使用反向传播法
- 首先计算最后一层的误差
- 再一层层地反向求出各层的误差,直到倒数第二层
前向传播例子
假设有一个数据样本:
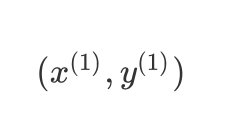
(x(1),y(1))({x^{(1)}},{y^{(1)}})(x(1),y(1))
神经网络是4层的,其中K=SL=L=4{K=S_L=L=4}K=SL=L=4
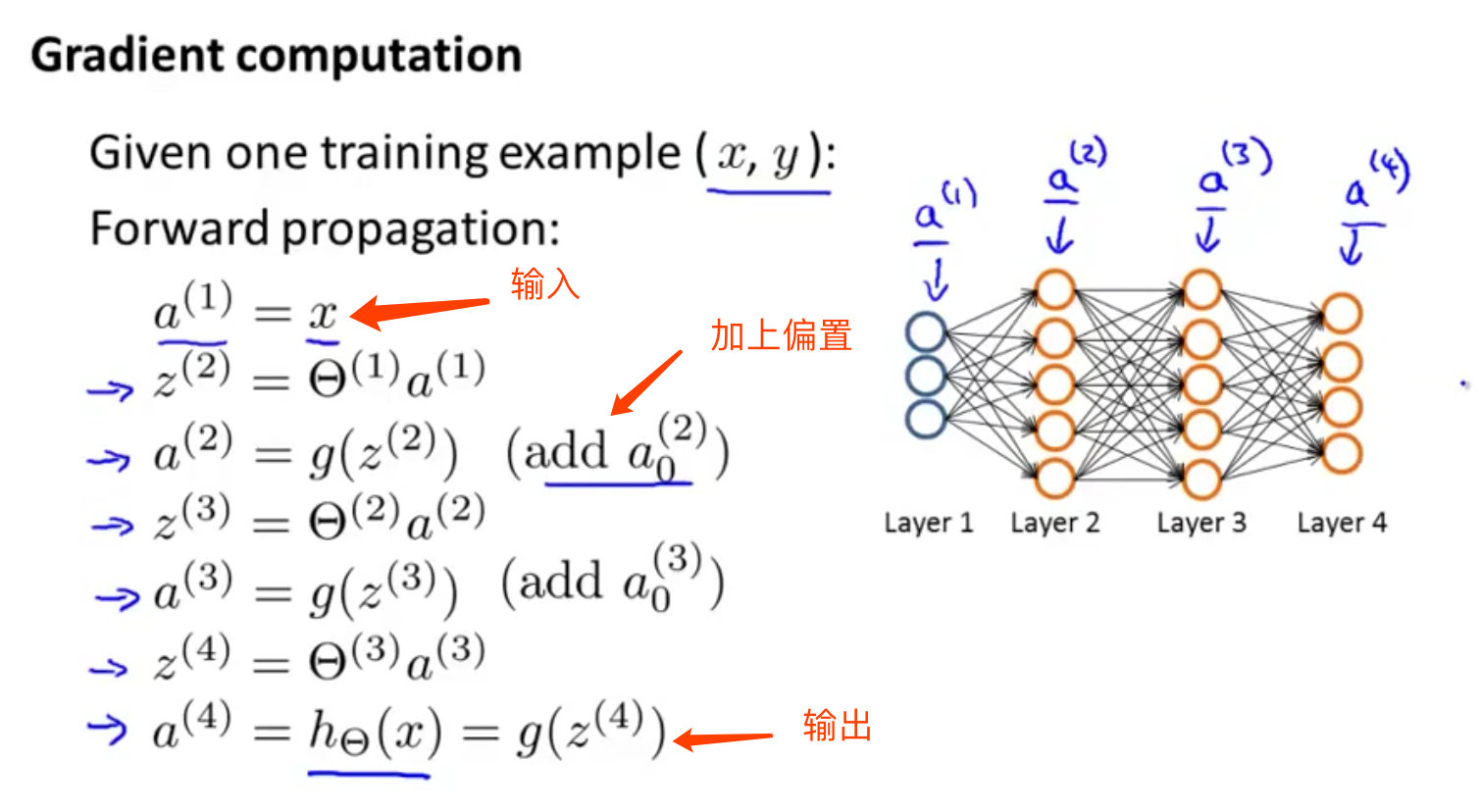
前向传播法就是通过一层层地按照神经网络的顺序从输入层到输出层计算下去。
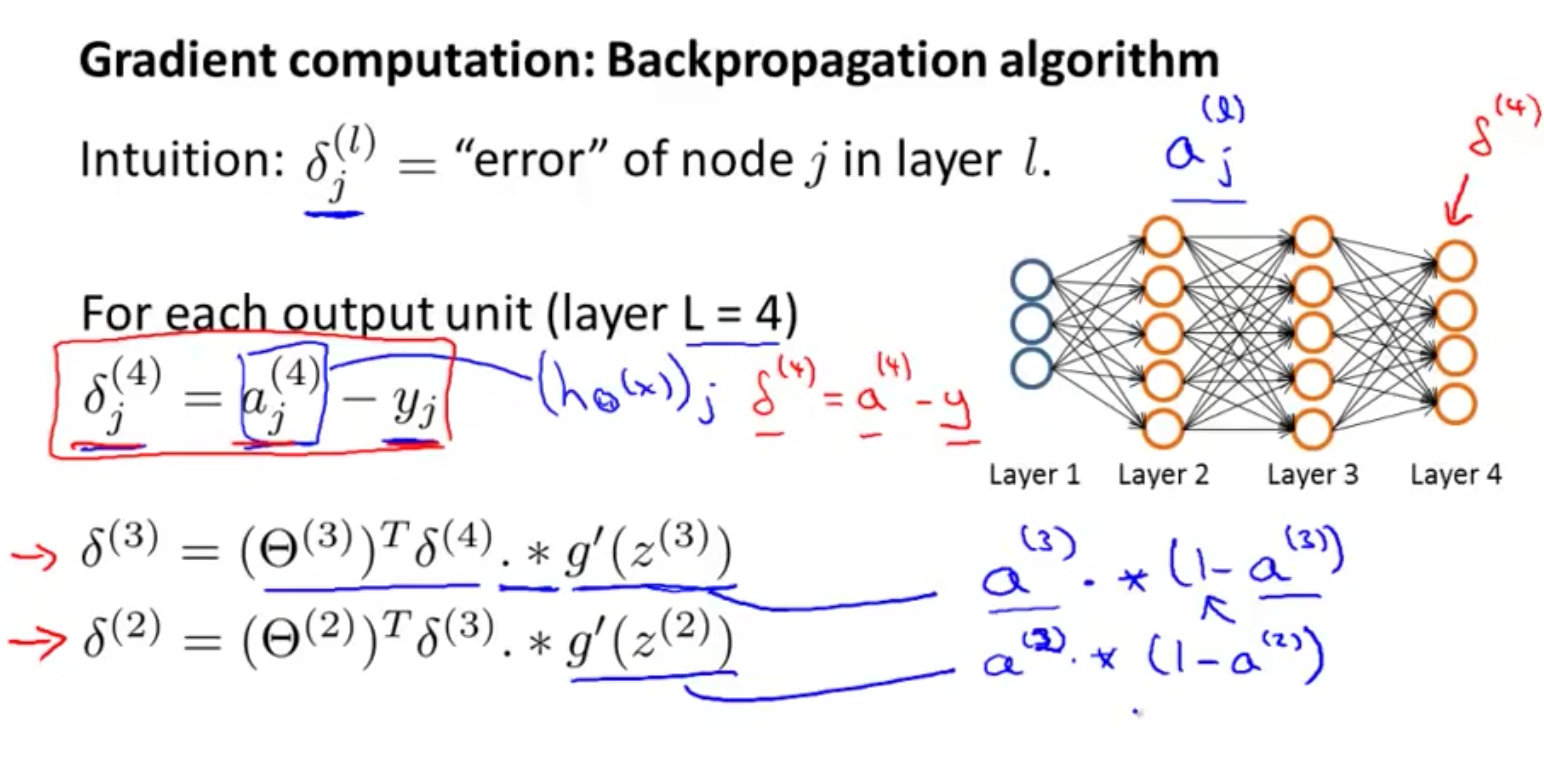
反向传播例子
-
从最后一层的误差开始计算:

误差=激活单元的预测a(4){a}^{(4)}a(4)和实际值之间的y(k)y^{(k)}y(k)之间的差
-
用δ\deltaδ表示误差,误差=模型预测值-真实值
δ(4)=a(4)−y \delta^{(4)} = a^{(4)} -y δ(4)=a(4)−y
-
前一层的误差
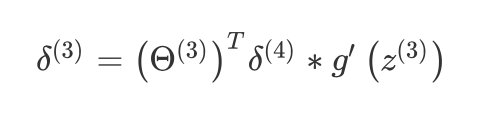
δ(3)=(Θ(3))Tδ(4)∗g′(z(3))\delta^{(3)}=\left({\Theta^{(3)}}\right)^{T}\delta^{(4)}\ast g'\left(z^{(3)}\right)δ(3)=(Θ(3))Tδ(4)∗g′(z(3))
其中 g′(z(3))g'(z^{(3)})g′(z(3))是 SSS 形函数的导数,具体表达式为:
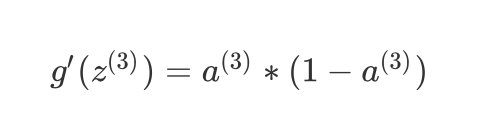
g′(z(3))=a(3)∗(1−a(3))g'(z^{(3)})=a^{(3)}\ast(1-a^{(3)})g′(z(3))=a(3)∗(1−a(3))
- 再前一层的误差
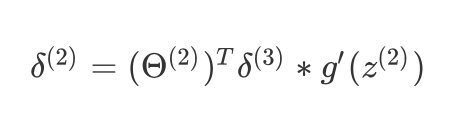
$ \delta{(2)}=(\Theta{(2)}){T}\delta{(3)}\ast g’(z^{(2)})$
第一层是输入变量,不存在误差
- 假设λ=0\lambda=0λ=0,如果不做正则化处理时
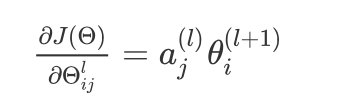
∂J(Θ)∂Θijl=aj(l)θi(l+1) \frac{\partial J(\Theta)}{\partial \Theta_{ij}^{l}}=a_j^{(l)}\theta_i^{(l+1)} ∂Θijl∂J(Θ)=aj(l)θi(l+1)
对上面的式子中各个上下标的含义进行解释:
-
lll代表的是第几层
-
jjj代表的是计算层中的激活单元的下标
-
iii代表的是误差单元的下标
算法

-
利用正向传播方法计算每层的激活单元
-
利用训练集的真实结果与神经网络的预测结果求出最后一层的误差
-
最后利用该误差运用反向传播法计算出直至第二层的所有误差。
在求出:△(l)ij\triangle {(l)}_{ij}△(l)ij之后,便可以计算代价函数的偏导数之后,便可以计算代价函数的偏导数:
D(l)ijD{(l)}_{ij}D(l)ij
反向传播的直观理解
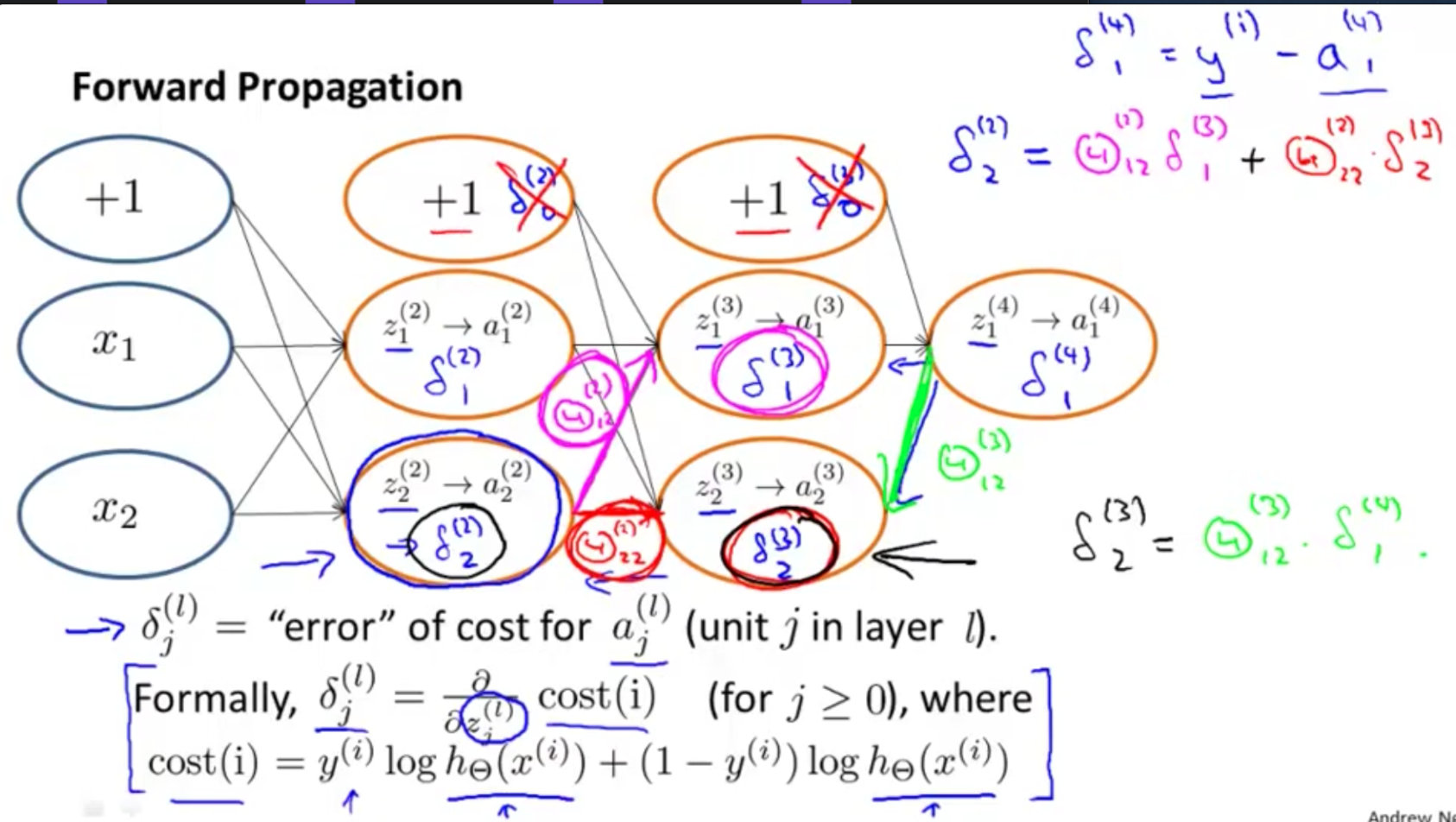
前向传播原理
- 2个输入单元;2个隐藏层(不包含偏置单元);1个输出单元
- 上标iii表示的是第几层,下标表示的是第几个特征或者说属性
图中有个小问题,看截图的右下角!!!
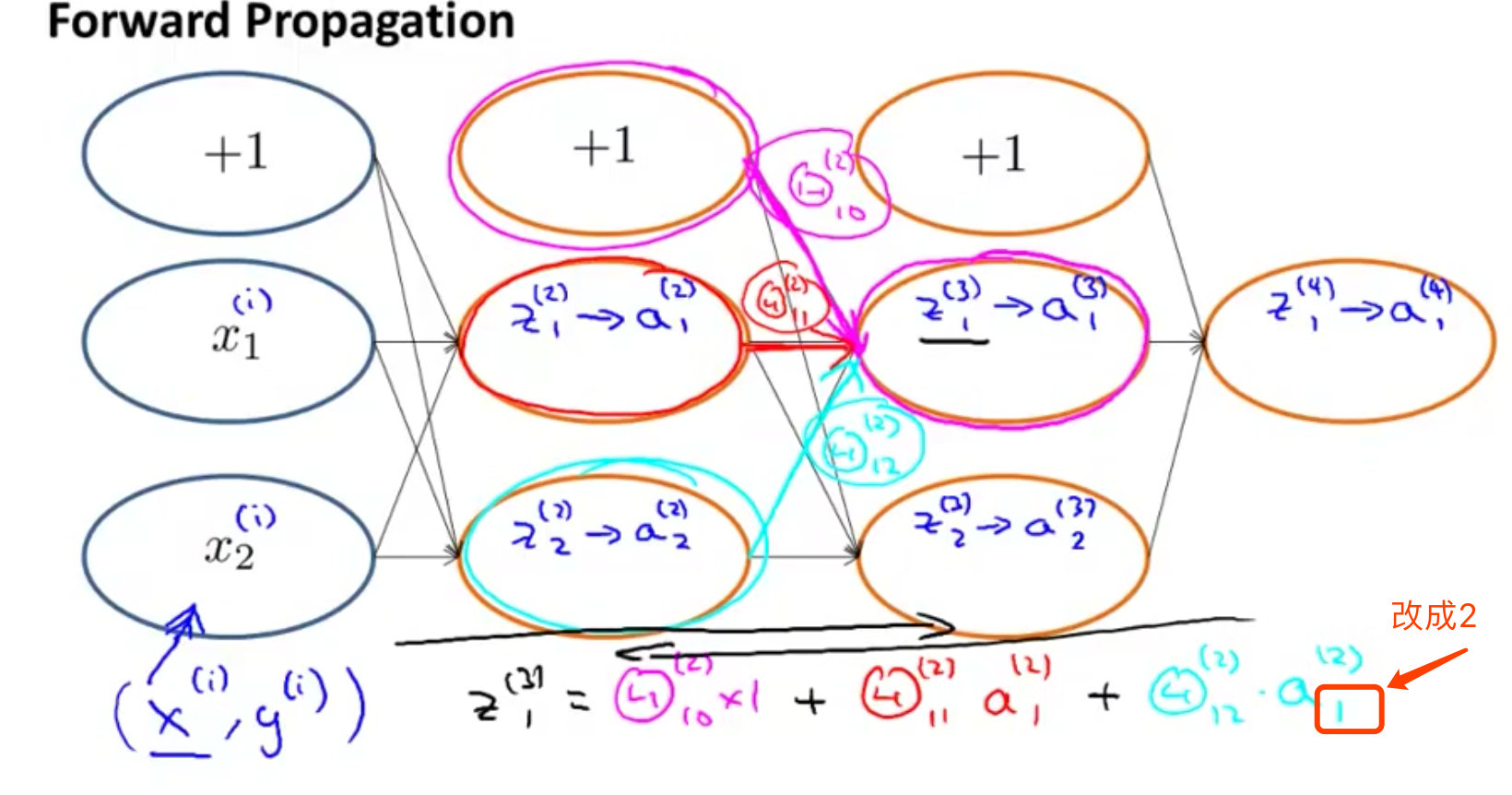
根据上面的反向传播法得到的结论:
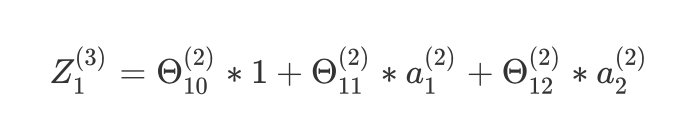
Z1(3)=Θ10(2)∗1+Θ11(2)∗a1(2)+Θ12(2)∗a2(2) Z^{(3)}_{1}=\Theta_{10}^{(2)}*1+\Theta_{11}^{(2)}*a^{(2)}_1+\Theta_{12}^{(2)}*a^{(2)}_2 Z1(3)=Θ10(2)∗1+Θ11(2)∗a1(2)+Θ12(2)∗a2(2)
反向传播原理
 )
)
参数展开
上面的式子中实现了怎么利用反向传播法计算代价函数的导数,在这里介绍怎么将参数从矩阵形式展开成向量形式


梯度检验
如何求解在某点的导数
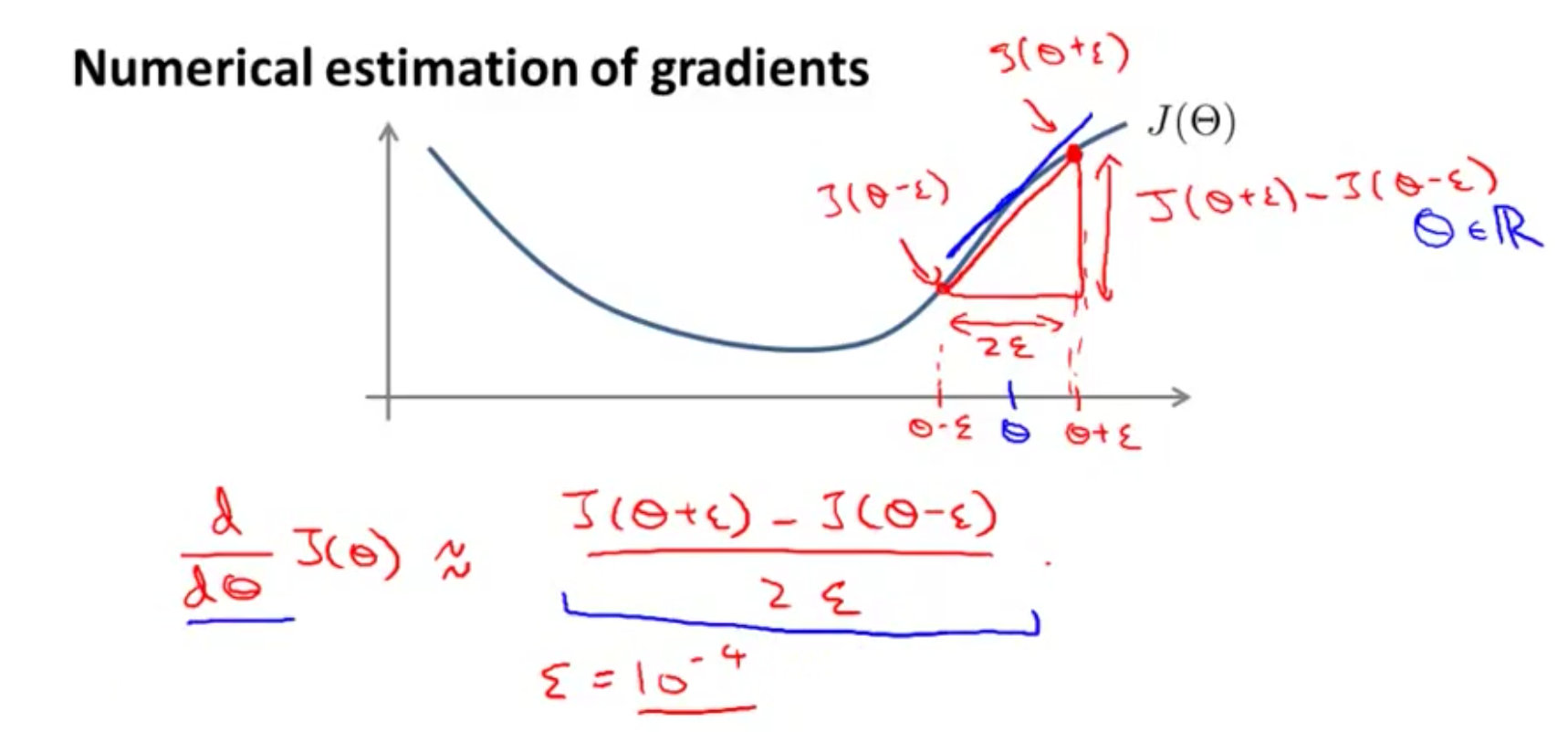
在代价函数中怎么对某个参数θθ求导

神经网络小结
首要工作
在构建神经网络的时候,首先考虑的是如何选择网络结构:多少层和每层多少个神经单元
- 第一层的单元数即我们训练集的特征数量。
- 最后一层的单元数是我们训练集的结果的类的数量。
- 如果隐藏层数大于1,确保每个隐藏层的单元个数相同,通常情况下隐藏层单元的个数越多越好。
训练神经网络步骤
- 参数的随机初始化
- 利用正向传播方法计算所有的hθ(x)h_{\theta}(x)hθ(x)
- 编写计算代价函数 JJJ的代码
- 利用反向传播方法计算所有偏导数
- 利用数值检验方法检验这些偏导数
- 使用优化算法来最小化代价函数
更多推荐
 已为社区贡献8条内容
已为社区贡献8条内容








所有评论(0)