本系列博客基于温州大学黄海广博士的机器学习课程的笔记，小伙伴们想更详细学习黄博士课程请移步到黄博士的Github、或者机器学习初学者公众号，现在在中国慕课也是可以学习的，内容包括机器学习、深度学习及Python编程，matplotlib、numpy、pandas、sklearn等，资料很详细，要系统学习请移步哦！笔者的博客只是笔记，内容不会十分详细，甚至会有些少错误！

1.人工神经网络简史

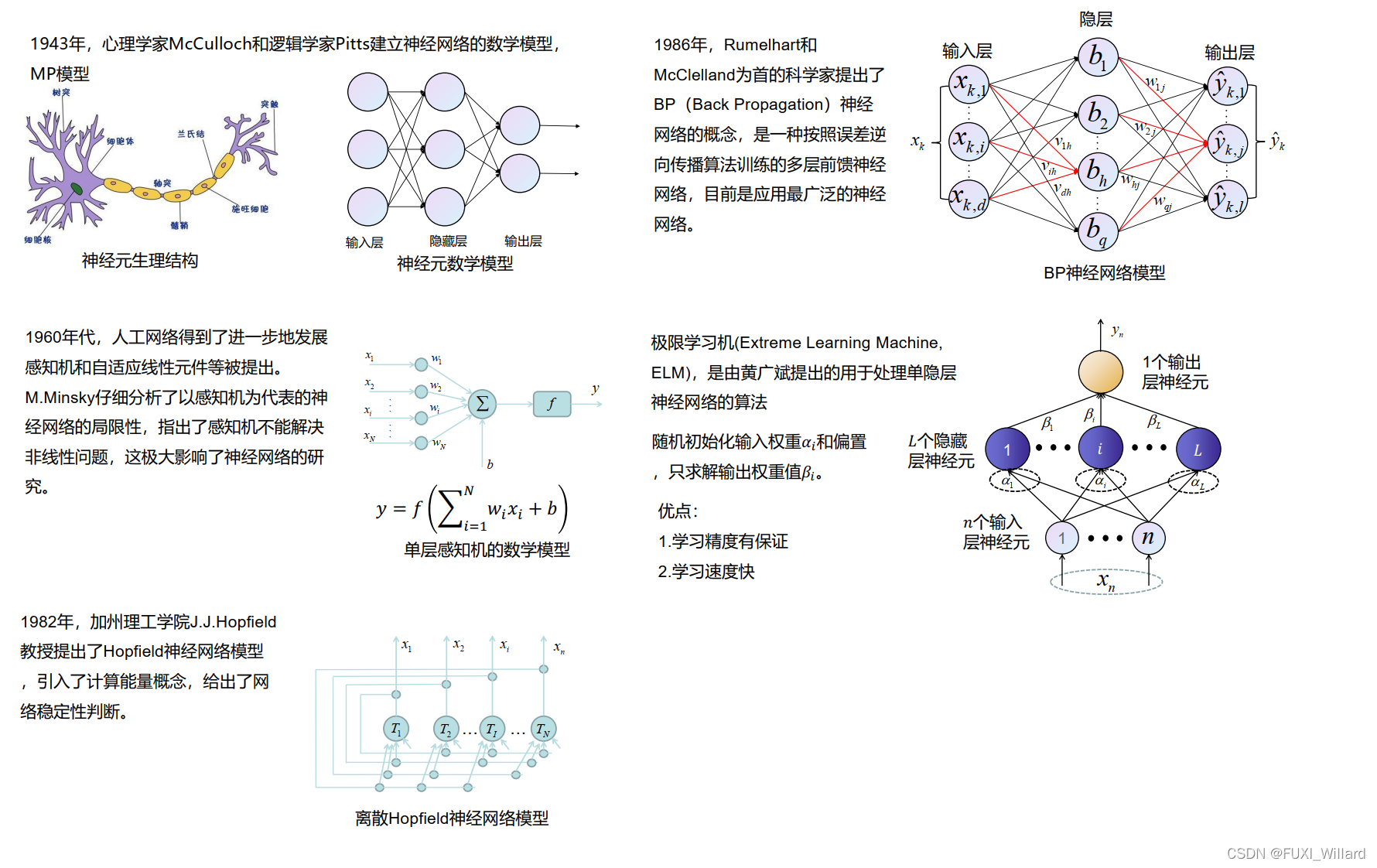
2.感知机算法

1. 感知机：一个二分类问题的线性分类模型；
2. 用$X\in R^{n\times d}$表示数据集，用$Y$表示标签；
3. 需要学习的目标函数：
   $$f(x)=sign({\omega }^{T}x+b)$$
4. 从输入输出中学习模型参数$\omega$和$b$；
5. 随机选择模型参数的$({\omega }_0,b_0)$初始值；
6. 选择一个训练样本$(x_n,y_n)$；
   若判别函数${\omega }^T{x}_n+b>0，且y_n=-1$，则$\omega =\omega -x_n，b=b-1$；
   若判别函数${\omega }^T{x}_n+b<0，且y_n=+1$，则$\omega =\omega +x_n，b=b+1$；
   再选取另一训练样本$(x_m,y_m)$，重复上述步骤；
   终止条件：直到所有数据的输入输出对都不满足上述条件，则退出循环；
7. 注：单层感知机只能处理线性问题，无法处理非线性问题；
   

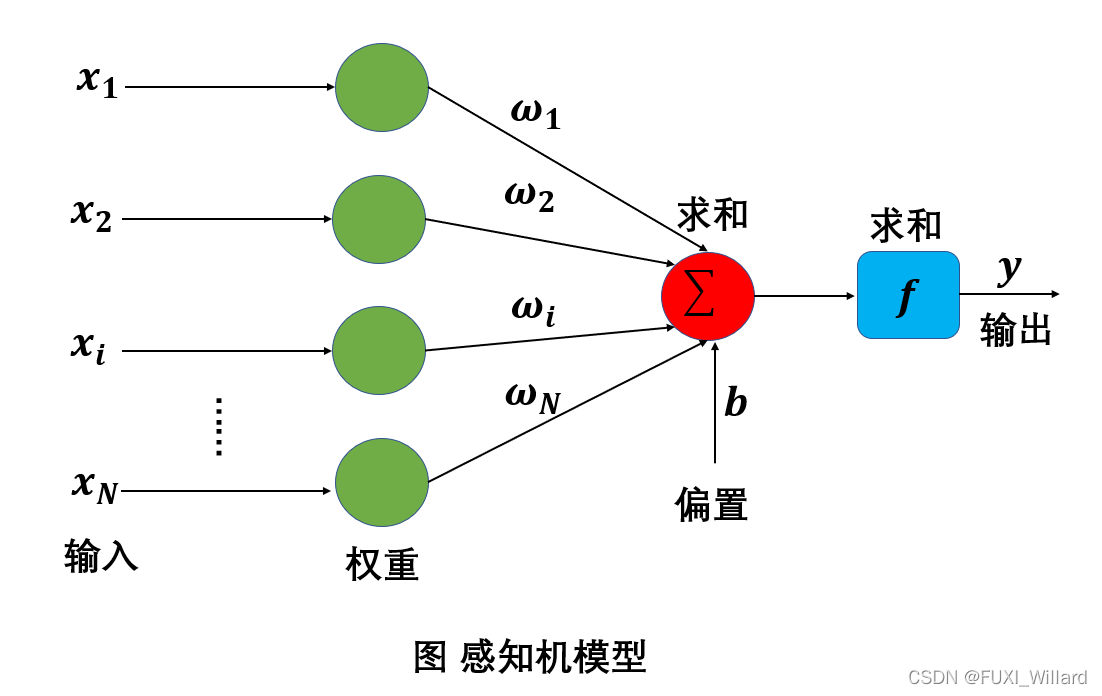
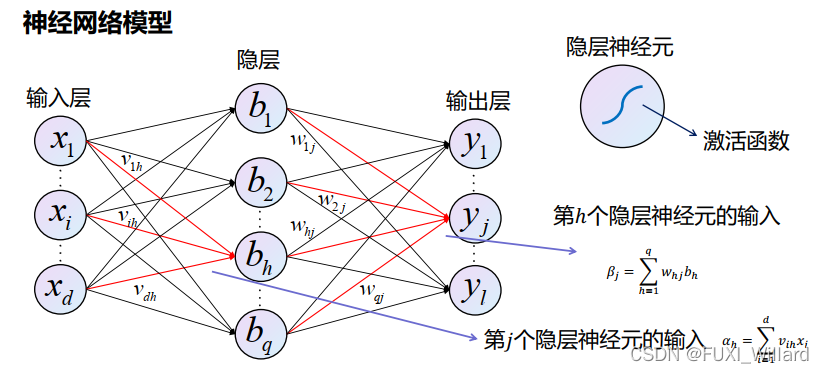
3.BP算法

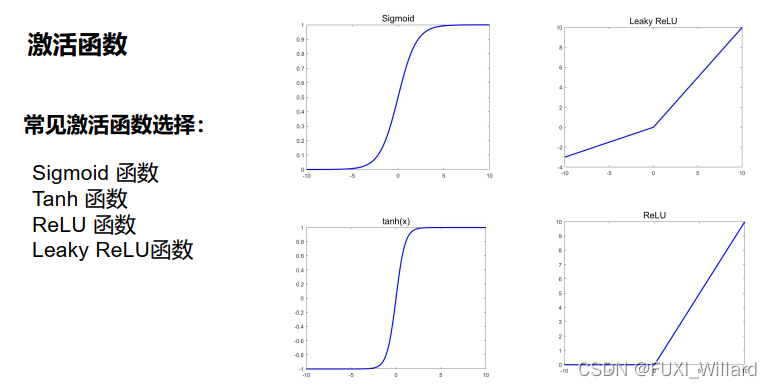
3.1 Sigmoid函数优缺点

• 优点
  1. 函数处处连续，便于求导；
  2. 可将函数值的范围压缩到$[0,1]$，可用于压缩数据，且幅度不变；
  3. 便于前向传输；
• 缺点
  1. 在趋于无穷的地方，函数值变化很小，容易出现梯度消失，不利于深层神经的反馈传输；
  2. 幂函数的梯度计算复杂；
  3. 收敛速度较慢；

3.2 算法步骤

1. 对样本明确预测输出值与损失函数；
2. 明确参数调整策略；
3. 计算输出层阈值的梯度；
4. 计算隐层到输出层连接权值的梯度；
5. 计算隐层阈值的梯度；
6. 计算输入层到隐层连接权值的梯度；
7. 引出归纳结论；

3.3 算法步骤详解

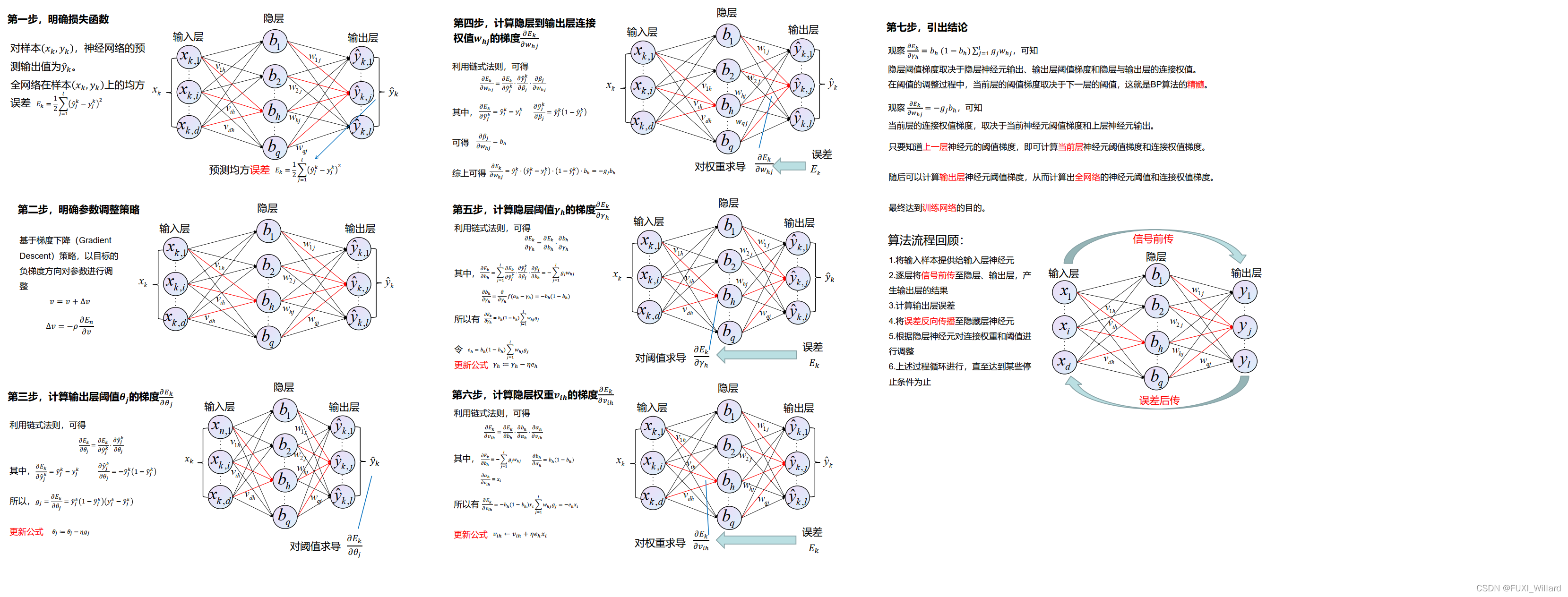
3.4 算法优缺点

• 优点
  1. 能够自适应、自主学习。BP可以根据预设参数更新规则，通过不断调整神经网络中的参数，以达到最符合期望的输出；
  2. 拥有很强的非线性映射能力；
  3. 误差的反向传播采用的是链式法则，推导过程严谨，科学；
  4. 算法泛化能力很强；
• 缺点
  1. BP神经网络参数众多，每次迭代需要更新较多数量的阈值和权值，收敛速度较慢；
  2. 网络中隐藏层含有的节点数目没有明确的准则，需要不断设置节点数试凑，根据网络误差结果最终确定隐藏层节点个数；
  3. BP算法是一种速度较快的梯度下降算法，容易陷入局部极小值的问题；