---

激活函数

激活函数的作用实在隐藏层引入非线性，使得神经网络能够学习和表示复杂的函数关系，使网络具备非线性能力，增强其表达能力

1. 基础概念

1.1 线性理解

如果在隐藏层不使用激活函数，那么整个神经网络会表现为一个线性模型。我们可以通过数学推导来展示这一点。

假设：

• 神经网络有$$L$$ 层，每层的输出为 $${\mathbf{a}}^{(l)}$$。
• 每层的权重矩阵为 $${\mathbf{W}}^{(l)}$$，偏置向量为$${\mathbf{b}}^{(l)}$$。
• 输入数据为$$\mathbf{x}$$，输出为$${\mathbf{a}}^{(L)}$$。

一层网络的情况

对于单层网络（输入层到输出层），如果没有激活函数，输出$${\mathbf{a}}^{(1)}$$ 可以表示为：
$${\mathbf{a}}^{(1)}={\mathbf{W}}^{(1)}\mathbf{x}+{\mathbf{b}}^{(1)}$$

两层网络的情况

假设我们有两层网络，且每层都没有激活函数，则：

• 第一层的输出：$${\mathbf{a}}^{(1)}={\mathbf{W}}^{(1)}\mathbf{x}+{\mathbf{b}}^{(1)}$$
• 第二层的输出：$${\mathbf{a}}^{(2)}={\mathbf{W}}^{(2)}{\mathbf{a}}^{(1)}+{\mathbf{b}}^{(2)}$$

将$${\mathbf{a}}^{(1)}$$代入到$${\mathbf{a}}^{(2)}$$中，可以得到：

$${\mathbf{a}}^{(2)}={\mathbf{W}}^{(2)}({\mathbf{W}}^{(1)}\mathbf{x}+{\mathbf{b}}^{(1)})+{\mathbf{b}}^{(2)}$$

$${\mathbf{a}}^{(2)}={\mathbf{W}}^{(2)}{\mathbf{W}}^{(1)}\mathbf{x}+{\mathbf{W}}^{(2)}{\mathbf{b}}^{(1)}+{\mathbf{b}}^{(2)}$$

我们可以看到，输出$${\mathbf{a}}^{(2)}$$是输入$$\mathbf{x}$$的线性变换，因为：$${\mathbf{a}}^{(2)}={\mathbf{W}}^{\prime }\mathbf{x}+{\mathbf{b}}^{\prime }$$
其中$${\mathbf{W}}^{\prime }={\mathbf{W}}^{(2)}{\mathbf{W}}^{(1)}$$，$${\mathbf{b}}^{\prime }={\mathbf{W}}^{(2)}{\mathbf{b}}^{(1)}+{\mathbf{b}}^{(2)}$$。

多层网络的情况

如果有$$L$$层，每层都没有激活函数，则第$$l$$层的输出为：$${\mathbf{a}}^{(l)}={\mathbf{W}}^{(l)}{\mathbf{a}}^{(l-1)}+{\mathbf{b}}^{(l)}$$

通过递归代入，可以得到：
$${\mathbf{a}}^{(L)}={\mathbf{W}}^{(L)}{\mathbf{W}}^{(L-1)}\cdots {\mathbf{W}}^{(1)}\mathbf{x}+{\mathbf{W}}^{(L)}{\mathbf{W}}^{(L-1)}\cdots {\mathbf{W}}^{(2)}{\mathbf{b}}^{(1)}+{\mathbf{W}}^{(L)}{\mathbf{W}}^{(L-1)}\cdots {\mathbf{W}}^{(3)}{\mathbf{b}}^{(2)}+\cdots +{\mathbf{b}}^{(L)}$$
表达式可简化为：
$${\mathbf{a}}^{(L)}={\mathbf{W}}^{\prime \prime }\mathbf{x}+{\mathbf{b}}^{\prime \prime }$$
其中，$${\mathbf{W}}^{\prime \prime }$$ 是所有权重矩阵的乘积，$${\mathbf{b}}^{\prime \prime }$$是所有偏置项的线性组合。

如此可以看得出来，无论网络多少层，意味着：

整个网络就是线性模型，无法捕捉数据中的非线性关系。

激活函数是引入非线性特性、使神经网络能够处理复杂问题的关键。

1.2 非线性可视化

我们可以通过可视化的方式去理解非线性的拟合能力：TensorFlow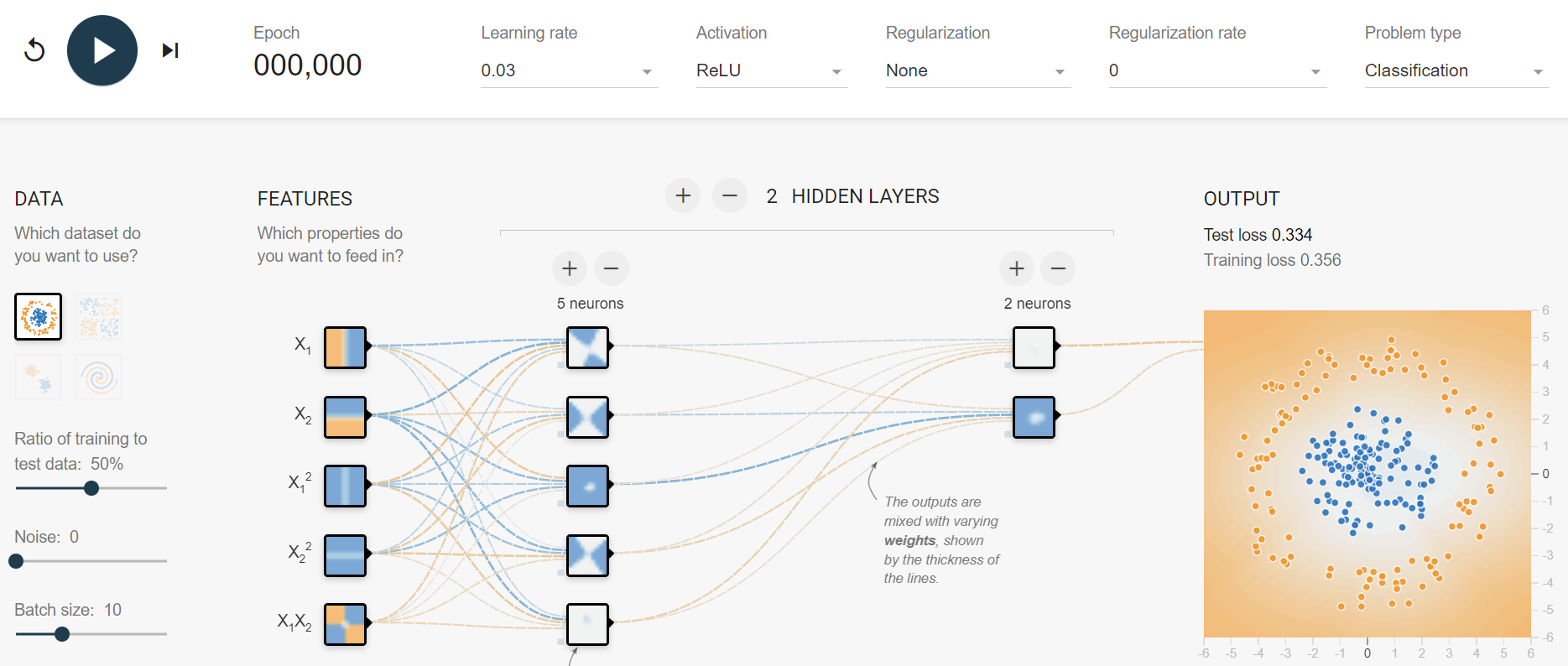

常见激活函数

激活函数通过引入非线性来增强神经网络的表达能力，对于解决线性模型的局限性至关重要。由于反向传播算法（BP）用于更新网络参数，因此激活函数必须是可微的，也就是说能够求导。

2. Sigmoid 函数

公式：

Sigmoid 函数的数学表达式为：

$$\sigma (x)=\frac{1}{1+e^{-x}}$$

特征：

• 输出范围：Sigmoid 函数的输出值在 (0, 1) 之间，通常用于概率预测。
• 平滑性：Sigmoid 函数是平滑的，在整个实数轴上都有定义。
• 可导性：Sigmoid 函数在所有点上都有导数，适用于梯度下降算法。

缺点：

• 梯度消失问题：当输入值过大或过小时，梯度变得非常小，导致梯度下降更新缓慢。这会使得模型训练变得缓慢或停滞，尤其在深层网络中更为严重。
• 输出非零中心：Sigmoid 函数的输出始终是正值，导致更新过程中可能会产生偏移，从而影响学习效率。

绘制：

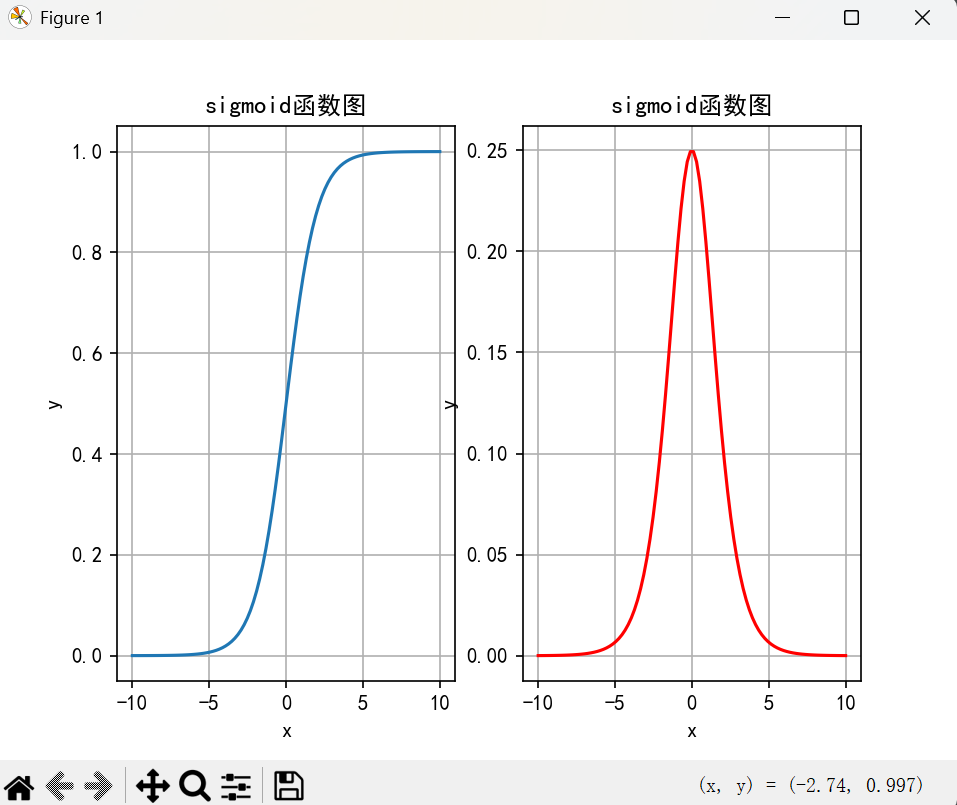
Sigmoid 函数的图像呈“S”型，输出值在 0 和 1 之间。

import numpy as np
import matplotlib.pyplot as plt

x = np.linspace(-10, 10, 1000)
y = 1 / (1 + np.exp(-x))

plt.plot(x, y)
plt.title('Sigmoid Activation Function')
plt.xlabel('x')
plt.ylabel('sigmoid(x)')
plt.grid(True)
plt.show()

适用场景：

• 输出层：常用于二分类问题的输出层，输出为概率值。
• 隐藏层：虽然 Sigmoid 在早期的网络中广泛使用，但因梯度消失问题，已被其他激活函数取代。

---

3. Tanh 函数

公式：

Tanh 函数的数学表达式为：

$$\tanh (x)=\frac{e^x-e^{-x}}{e^x+e^{-x}}$$

特征：

• 输出范围：Tanh 的输出值在 (-1, 1) 之间，具有零中心性，这有助于加速训练。
• 平滑性：Tanh 函数平滑且可导，适用于梯度下降。
• 梯度消失问题：与 Sigmoid 类似，Tanh 也存在梯度消失问题，但相较于 Sigmoid，Tanh 的梯度值在 (-1, 1) 范围内有更强的表达能力。

缺点：

• 梯度消失问题：当输入值过大或过小时，Tanh 的梯度仍然趋近于 0，导致训练变慢。

绘制：

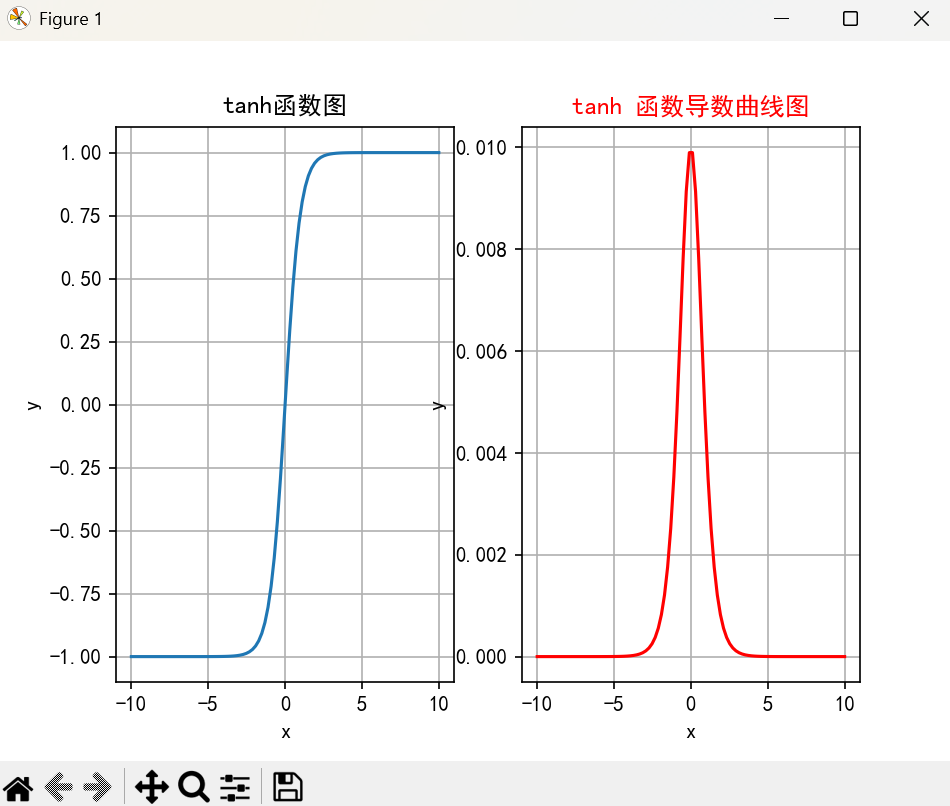
Tanh 函数的图像呈“S”型，但输出在 -1 和 1 之间。

y = np.tanh(x)

plt.plot(x, y)
plt.title('Tanh Activation Function')
plt.xlabel('x')
plt.ylabel('tanh(x)')
plt.grid(True)
plt.show()

适用场景：

• 隐藏层：Tanh 在隐层中比 Sigmoid 更常见，适合在输入数据分布较为对称的情况下使用。
• 输出层：不常用于输出层，除非需要输出在 (-1, 1) 范围内。

---

4. ReLU 函数

公式：

ReLU 函数的数学表达式为：

$$\text{ReLU}(x)=\max (0,x)$$

特征：

• 输出范围：ReLU 输出值在 [0, ∞) 之间。对于负输入，输出为 0。
• 简单高效：ReLU 是目前最常用的激活函数之一，计算简单且非常高效，适用于深层神经网络。
• 避免梯度消失：ReLU 对正数输入具有恒定的梯度，这有助于避免梯度消失问题。

缺点：

• Dying ReLU 问题：当神经元的输入始终为负时，ReLU 的输出为 0，导致该神经元在训练过程中“死掉”，无法更新。
• 非零中心性：ReLU 函数输出为正，可能会导致训练过程中出现不对称的更新。

绘制：

ReLU 函数的图像呈“L”型。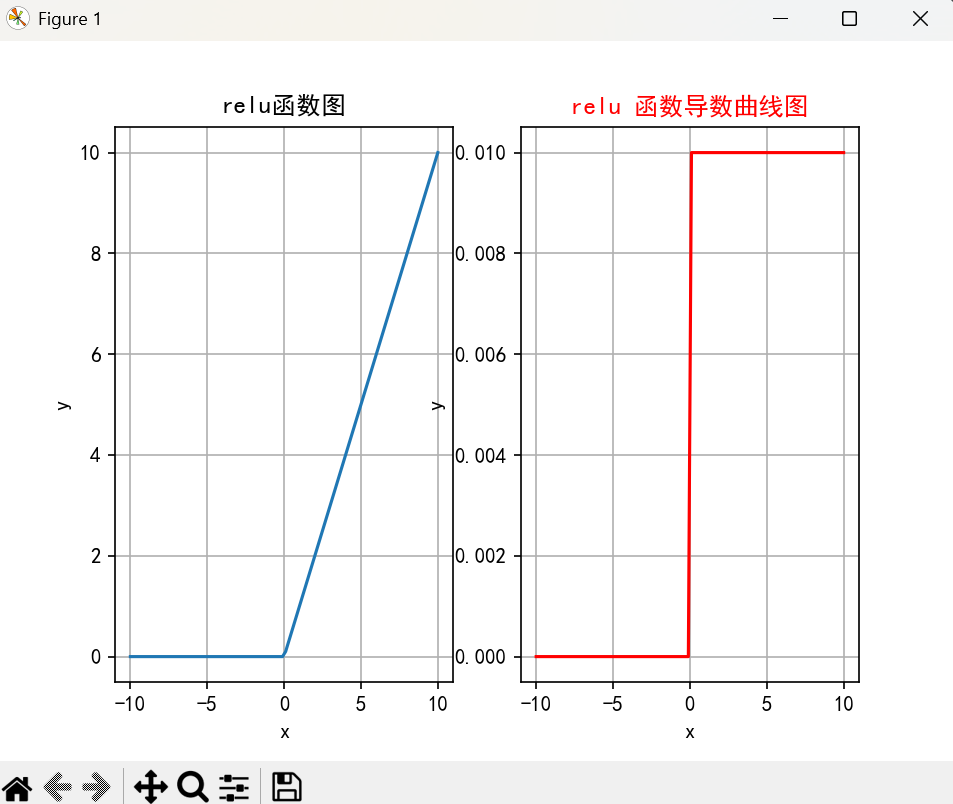

y = np.maximum(0, x)

plt.plot(x, y)
plt.title('ReLU Activation Function')
plt.xlabel('x')
plt.ylabel('ReLU(x)')
plt.grid(True)
plt.show()

适用场景：

• 隐藏层：ReLU 函数通常用于隐藏层，尤其是在深度网络中，能够加速训练过程并有效避免梯度消失。
• 输出层：不常用于输出层，因为输出需要具备一定的范围。

---

5. Leaky ReLU 函数

公式：

Leaky ReLU 函数的数学表达式为：

$$\text{Leaky ReLU}(x)=\max (\alpha x,x)$$

其中 $\alpha$ 是一个小的常数（例如 0.01）。

特征：

• 输出范围：与 ReLU 类似，但对于负输入，Leaky ReLU 会有一个小的负值输出，而不是完全为 0。
• 避免 Dying ReLU 问题：Leaky ReLU 在负值区域有一个斜率，避免了神经元死掉的问题。
• 可调性：通过调整 $\alpha$ 参数，可以控制负值部分的斜率。

缺点：

• 非零中心性：尽管 Leaky ReLU 避免了 Dying ReLU 问题，但它的输出仍然是非零中心的，可能会导致一些训练上的不对称性。

绘制：

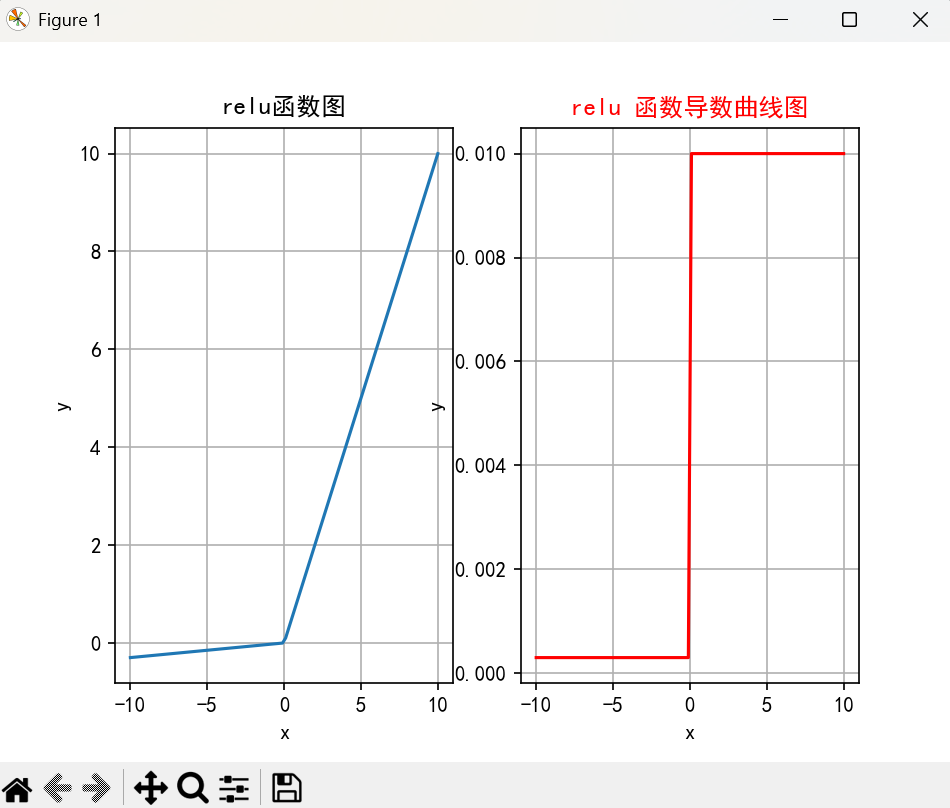
Leaky ReLU 函数的图像类似于 ReLU，但负值区域具有一个小斜率。

alpha = 0.01
y = np.maximum(alpha * x, x)

plt.plot(x, y)
plt.title('Leaky ReLU Activation Function')
plt.xlabel('x')
plt.ylabel('Leaky ReLU(x)')
plt.grid(True)
plt.show()

适用场景：

• 隐藏层：Leaky ReLU 常用于隐藏层，可以有效避免 Dying ReLU 问题。

---

6. Softmax 函数

公式：

Softmax 函数的数学表达式为：

$$\text{Softmax}(x_i)=\frac{e^{x_i}}{{\sum }_j{e}^{x_j}}$$

其中 $x_i$ 是输入向量中的第 $i$ 个元素。

特征：

• 输出范围：Softmax 输出一个概率分布，所有输出值都在 [0, 1] 之间，且所有输出值之和为 1。
• 用于多分类：Softmax 常用于多分类任务的输出层，用于将模型的输出转化为概率分布。
• 平滑性：Softmax 函数平滑并具有可导性，适用于梯度下降优化。

缺点：

• 计算开销大：对于多类别任务，Softmax 需要计算指数和求和，计算开销较大。
• 容易过拟合：Softmax 会把某一类的概率过度偏向最大值，可能导致过拟合。

绘制：

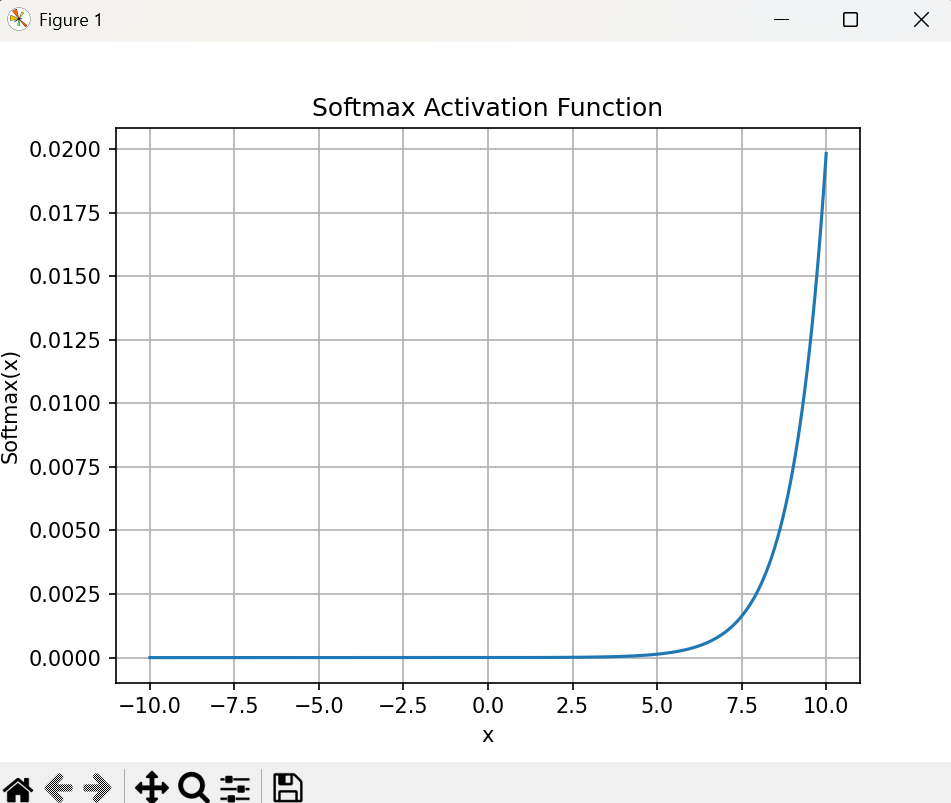
Softmax 函数的输出通常用于多分类问题，其输出值在 [0, 1] 之间，并且和为 1。

def softmax(x):
    e_x = np.exp(x - np.max(x))
    return e_x / e_x.sum(axis=0)

x = np.linspace(-10, 10, 1000)
y = softmax(x)

plt.plot(x, y)
plt.title('Softmax Activation Function')
plt.xlabel('x')
plt.ylabel('Softmax(x)')
plt.grid(True)
plt.show()

适用场景：

• 输出层：Softmax 用于多分类任务的输出层，转换模型的原始输出为概率分布。

---

如何选择激活函数？

1. 隐藏层激活函数的选择：

• ReLU 是最常见的选择，特别是在深层神经网络中，因为它可以加速训练并减少梯度消失问题。
• Leaky ReLU 可以用于避免 Dying ReLU 问题，适合在有很多层的网络中使用。

2. 输出层激活函数的选择：

• Sigmoid：常用于二分类任务的输出层，输出值可以理解为概率。
• Softmax：用于多分类任务的输出层，将网络输出转化为概率分布。

---

总结：

选择合适的激活函数对于神经网络的训练和性能至关重要。一般来说，隐藏层推荐使用 ReLU 或 Leaky ReLU，而输出层的激活函数则依赖于具体任务，二分类任务使用 Sigmoid，多分类任务使用 Softmax。