【机器学习：初学者自述】二、线性回归、最小二乘法和梯度下降

我们先从简单的讲起。先研究监督学习--回归--线性回归。如果认真学习过线性代数的最小二乘法，也希望不要直接点击关闭。

华师大别拿材料折磨我谢谢

1468人浏览 · 2024-09-04 21:55:08

华师大别拿材料折磨我谢谢 · 2024-09-04 21:55:08 发布

我们先从简单的讲起。先研究监督学习--回归--线性回归。

如果认真学习过线性代数的最小二乘法，也希望不要直接点击关闭。因为这和矩阵解法不太相同，它涉及到一个新的方法：梯度下降算法(gradient descent algorithm)。

一、线性回归

首先看以下回归的过程：

数据集-->训练得到函数-->由输入特征得到标签。

对于得到的函数我们自然知道如何利用。我们输入x，代入函数即可得到y。但是如何训练得到函数呢？

在这里，我们举个例子，我们已经有一系列的数据：

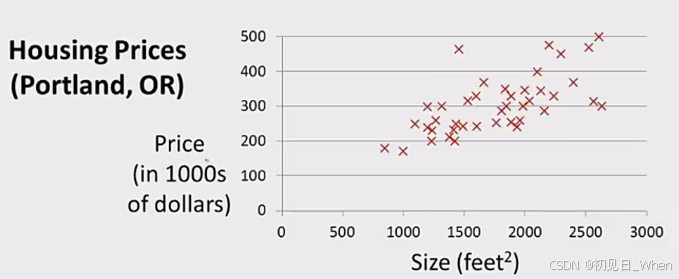
假设我们确定用一条直线，来表达上述房价和房子大小的关系。那么首先根据初中数学知识可知，线性函数的基本模型（model)是：

$f_{(w,b)}(x) = wx + b$

那么我们要做的，难道是一个个w,b代入进去尝试，然后比较哪个更符合我们要的模型吗？显然这不可能。那么要求出最佳的w,b，需要考虑最小二乘法。

二、最小二乘法

（1）成本函数

在这里我们先介绍一个东西，叫做成本函数(cost function)。可以想象，我们拟合的直线，对于数据集中的每一组数据，可能都会存在误差。当所有误差累加起来，最后取平均的时候，大致就代表了整条直线对于数据集的误差。

$error = f_{w,b} (x^{(i)}) - y^{(i)} = \hat{y}^{(i)} - y^{(i)}$

这里的含义是，误差为拟合直线预测的值减去实际值。在这里，我们通常对误差给上平方消除正负影响，随后累加：

$\sum_{i=1}^{m} (f_{w,b}(x^{(i)})-y^{(i)})^2$

再取个平均，得到了：

$\frac{1}{m} \sum_{i=1}^{m} (f_{w,b}(x^{(i)})-y^{(i)})^2$

这就表示了我们所说的整条直线对于数据集的误差。当然对于机器学习来说，通常我们喜欢再除以2，让公式看起来更整洁（我也不知道为什么好看），于是就得到了成本函数,这里我们使用字母j表示，于是有：

$j(w,b) =\frac{1}{2m} \sum_{i=1}^{m} (f_{w,b}(x^{(i)})-y^{(i)})^2$

我们所希望的当然是整条直线对数据集的误差越小越好。即：

$Minimize \frac{1}{2m} \sum_{i=1}^{m} (f_{w,b}(x^{(i)})-y^{(i)})^2$

（2）最小二乘法

i. 简化分析

我们这里要注意， $j(w,b)$ 是关于w,b的二元函数。我们先讨论只有w（即b=0）的特殊情况，则此时我们的模型变为：

$f(x) = wx$

同样我们用一个极为简单的数据集来研究，这个数据集中只有三个数据：

x	y
1	1
2	2
3	3

画在图像上就是：

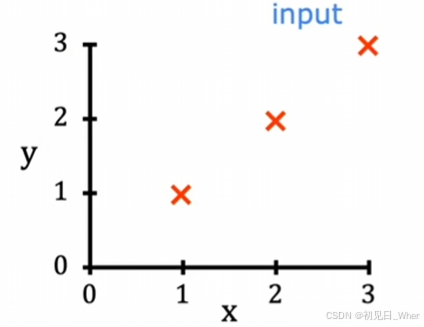
我们的大脑告诉我们，只要让w=1就可以完美拟合了。但是机器程序是不知道的。不过我们刚才已经学过了成本函数，我们可以列举出若干个w，比较各自的成本函数值。于是我们尝试了多个w，得到以下表格：

w	j
-0.5	5.85
0	2.33
0.5	0.58
1	0
1.5	0.58

计算更多的w值，我们能得到 $j(w)$ 的曲线：

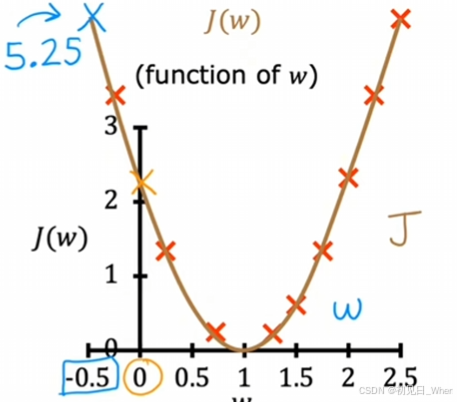
可以看出是一条抛物线。这里我们不对它是一条怎样的线条细致研究。我们感兴趣的地方在于它的最小值点正好就是w=1处。

可见w=1正好满足了使成本函数最小化的目的。因此在这个逻辑上，我们采用w=1来拟合我们的函数。

ii. 常规分析

当然，上述是仅有w的特殊情况。如果涉及到了b的该如何呢？

涉及到b的时候，成本函数就成为了二元函数。我们应该采用二元函数的处理方法。计算方法和前文是一致的，都是代入若干个数据，得到图像。涉及到二元图像的时候，我们需要用到其他工具分析。

在学习高数的时候，我们学过用3D图像表示，这里我们可以利用Matlab绘制：

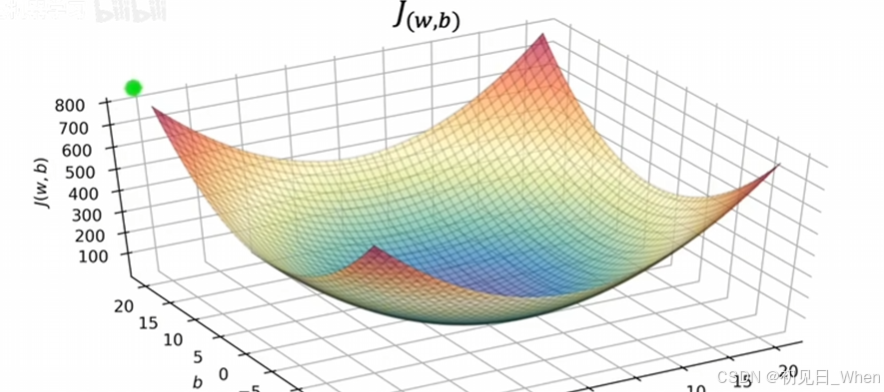
或者利用等高线：

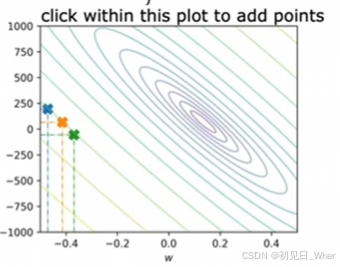
当然，这些都只是让二元函数更加直观的方法。我们的目的还是一致的，都是为了最小化成本函数。但如果涉及到三元、四元，就没有这样的图像让我们直观地“一眼看出”了。因此在后续将介绍梯度下降算法，以求出各种情况下的最小成本函数。

由此也可以很清晰地理解“最小二乘法”这个名字，也就是让“二乘”的值最小化。

三、梯度下降算法

（1）算法详解

我们已经知道了，最小化成本函数，能得到拟合效果最好的线条。但是还有问题尚未解决：我们的大脑能够从图像直观地看出结果，说：“这个点就是最小值点”；但是，程序没有那个直观阅读的能力；同时，如果数据涉及到多维的图像，我们人类也无法直接观测，这个时候，又如何找寻最小的点呢？

在这里，我们采用了梯度下降(gradient descent algorithm)算法。梯度下降算法不仅可用于线性回归，对于其他的回归方式，梯度下降算法同样适用。首先我们将高等数学中的梯度重述一遍：

梯度表示函数在某一点出的变化率最大。数学表示为：

$\frac{\partial }{\partial x}f(x,y) \vec{i}+\frac{\partial}{\partial y}f(x,y) \vec{j}$

如果我们要处理如下图的函数，思路是怎样的？（在这里，我们的x和y被w和b替换了）假设你处于任何一个地方，如下标点，目的地是谷底（valley）。而走向谷底最快的方法，当然是找坡度最陡的方向，向着这个方向行走一小步。到了一个新位置之后，再找寻这个位置的最陡方向，再往下行走一步，如此反复......这样我们就能保证自己到达了一个谷底。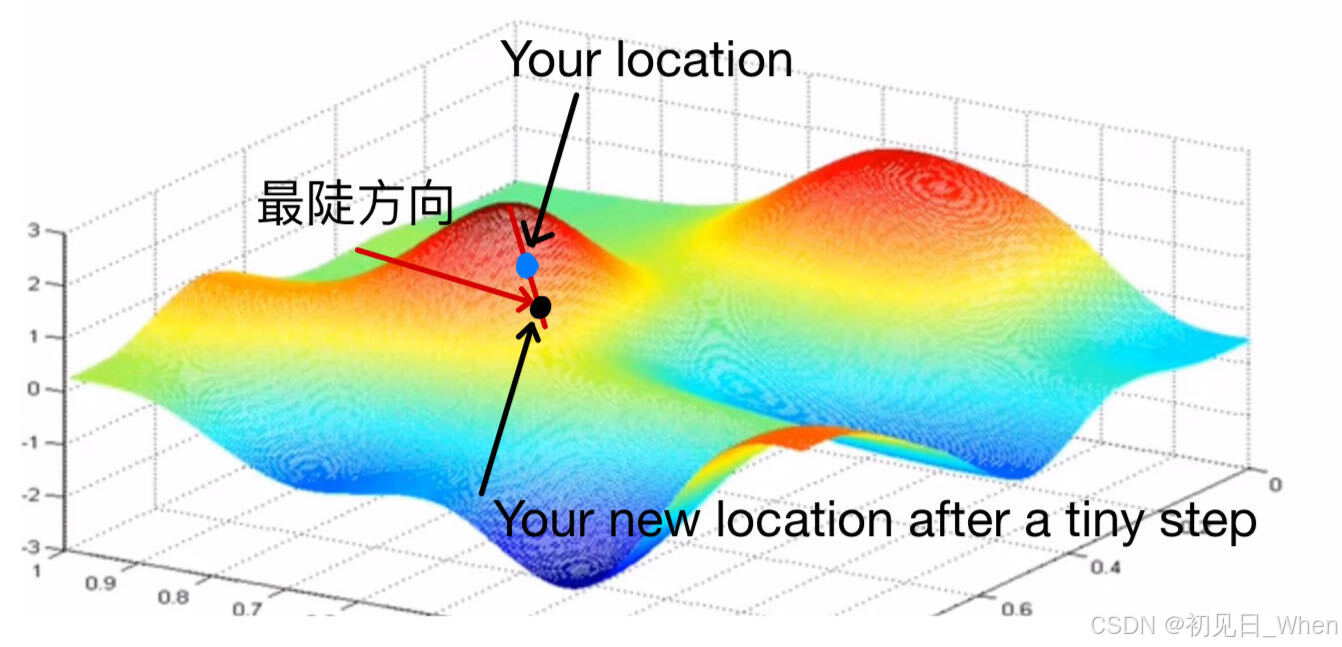现在我们分析一小步之后的情况。行走了一小步之后，我们的位置信息也发生了变化，对于i方向（即w轴方向），我们的w坐标值变化了：

$\frac{\partial }{\partial w}f(w,b)$

同理，j方向（即b轴方向），b坐标值变化了：

$\frac{\partial }{\partial b}f(w,b)$

假设我们的初始坐标是(w,b)，那么我们可以得出我们的新坐标：（注意，最陡的方向既可以“下山”，也可以“上山”。而我们要保证自己是下山。因此我们要将初始坐标减去这些变化值。）

$w_{new} = w -\frac{\partial }{\partial w}f(w,b)$

$b_{new} = b - \frac{\partial }{\partial w}f(w,b)$

上述公式表示：沿着初始点的坡度最陡的方向，下坡行走该点梯度值的距离。当然，我们忘记了一个重点，那就是沿着梯度迈出步伐的大小是恒定等于这个方向的梯度大小，即坐标值的变化量，恒等于该点偏导数值:

$w_{change} =1 \times \frac{\partial }{\partial w}f(w,b)$

$b_{change} =1 \times \frac{\partial }{\partial b}f(w,b)$

显然不太合理，如果这个点的偏导数太大，我们一下子就不知道跑到十万八千里之外去了。所以我们希望自己迈出一个尽量小的步伐，这样才能保证我们能够更加精确地前往谷底。因此这里还要再给一个参数，表示迈出的步伐的大小。这里，我们称之为学习率(learning rate)，用希腊字母 $\alpha$ 表示。从而我们的算法表示为：

$w_{new} = w -\alpha \times \frac{\partial }{\partial w}f(w,b)$

$b_{new} = b -\alpha \times \frac{\partial }{\partial b}f(w,b)$

（2）同时更新原则

如果让你将上述算法以代码形式表示的话，你可能会写成这样：

w = w - a * partial_w(w,b)
b = b - a * partial_b(w,b)

这样是一个经典的错误。因为没有满足原则：同时更新（Simultaneously update)。

代码的第一行，我们更新了w，但是第二行尚未更新。此时第二行使用的偏导partial_b(w,b）接收的参数却是已经更新过的w，这样导致的后果是：我们无法按照梯度的方向进行行走，甚至出现大幅度的偏移。

为保证同时更新，正确的写法应该是：

w_tmp = w - a * partial_w(w,b)
b_tmp = b - a * partial_b(w,b)
w = w_tmp
b = b_tmp

这样就能保证同时更新。

（3）线性回归模型中求偏导的推导

前文已经提到了partial_w(w,b），partial_b(w,b)函数，系统学习过微积分的当然知晓如何求偏导，但是如何在程序中实现却可能难住了大部分人。

这里主要讲解线性回归模型中求偏导：

首先已知成本函数表示如下：

$j(w,b) =\frac{1}{2m} \sum_{i=1}^{m} (f_{w,b}(x^{(i)})-y^{(i)})^2$

将 $f_{w,b}(x)$ 展开得到：

$j(w,b) =\frac{1}{2m} \sum_{i=1}^{m} (w\times x^{(i)} + b -y^{(i)})^2$

对w求偏导：

$\frac{\partial}{\partial w}j(w,b) =\frac{\partial}{\partial w}\frac{1}{2m} \sum_{i=1}^{m} (w\times x^{(i)} + b -y^{(i)})^2$

等同于这种复合求导：

$\frac{d}{dx}(kx + b)^2 = 2k(kx+b)$

注意此时w才是对应的上式的x，得到结果：

$\frac{\partial}{\partial w}j(w,b) =\frac{1}{2m} \sum_{i=1}^{m} (w\times x^{(i)} + b -y^{(i)}) \times 2x^{(i)} \\ = \frac{1}{m} \sum_{i=1}^{m}(wx^{(i)} + b - y^{(i)})x^{(i)}$

同理可得：

$\frac{\partial}{\partial b}j(w,b) = \frac{1}{m} \sum_{i=1}^{m}(wx^{(i)} + b - y^{(i)})$

请注意，这只是线性回归模型中偏导函数的推导，并不适合于所有的模型。同时，吴老师的课程中有对梯度下降算法更加直观的描述，因为这里重在复述思路，直观理解就不再复述了。

技术共进，成长同行——讯飞AI开发者社区

更多推荐

复杂性和人工智能对身份保护提出了考验

讯飞AI开发者社区

**发散创新：探索编程语言中的创新实践之路**随着技术的飞速发展，编程语言日新月异，创新成为了推动技术

随着技术的不断发展，编程语言的创新将带来更多可能性，为开发者提供更多施展才华的空间。本文简要介绍了编程语言的演变与创新、主流编程语言及其特点、如何在编程中发散创新、创新实践案例以及面临的挑战与机遇。本文将带领大家走进编程语言的创新世界，探讨如何在实际开发中发散创新，实现技术的突破与飞跃。从最初的机器语言到如今的面向对象、函数式编程等，编程语言的演变见证了计算机技术的飞速发展。随着云计算、物联网、人

讯飞AI开发者社区

让AI学会“温故而知新”：基于最近邻方法的智能新范式

在当今所有AI都在追求更大、更复杂的神经网络时，一股新的思潮正在悄然兴起：为什么不让我们AI系统像一个博闻强识的智者一样，通过“回忆”和“类比”过去的知识来解决新问题呢？它让我们看到，人工智能的未来，或许不是一味地追求更大的模型，而是走向一种“模型（大脑） + 数据库（记忆）” 的更优雅、更高效、也更接近人类思维的架构。它告诉我们，智能不仅在于抽象概括的能力，也在于精准回忆和灵活应用的经验。当AI