【机器学习】必备数学基础 笔记
〇、前情提要降维相关的知识点,特别是涉及PCA和SVD时,都会遇到求特征值和特征向量的计算,回忆计算过程。参考:1.【机器学习 必备数学基础】PCA降维/SVD奇异值分解中线性代数知识: 如何求解n阶方阵的特征值和特征向量?https://www.bilibili.com/video/BV1kE411371s?from=search&seid=5629878461143195813P1 0
〇、前情提要
降维相关的知识点,特别是涉及PCA和SVD时,都会遇到求特征值和特征向量的计算,回忆计算过程。
参考:
1.【机器学习 必备数学基础】PCA降维/SVD奇异值分解中线性代数知识: 如何求解n阶方阵的特征值和特征向量?
https://www.bilibili.com/video/BV1kE411371s?from=search&seid=5629878461143195813
P1 01-特征值和特征向量的定义
笔记

定理
设A=(aij) n阶方阵,若有数λ和非零列向量X,满足AX=λX,则λ为A的一个特征值,X为A的属于λ的一个特征向量。
AX=λX
AX-λX=0
(A-λE)X=0 关于X的齐次线性方程组
|A-λE|=0 系数行列式为零 求解基础
最终求得λ特征值和X的特征向量
齐次线性方程组
不带常数项
有非零解 系数行列式一定为零
n阶方阵
n阶方阵有n个特征值
P2 02-齐次线性方程组
笔记

概念

无b(常数项)
矩阵形式
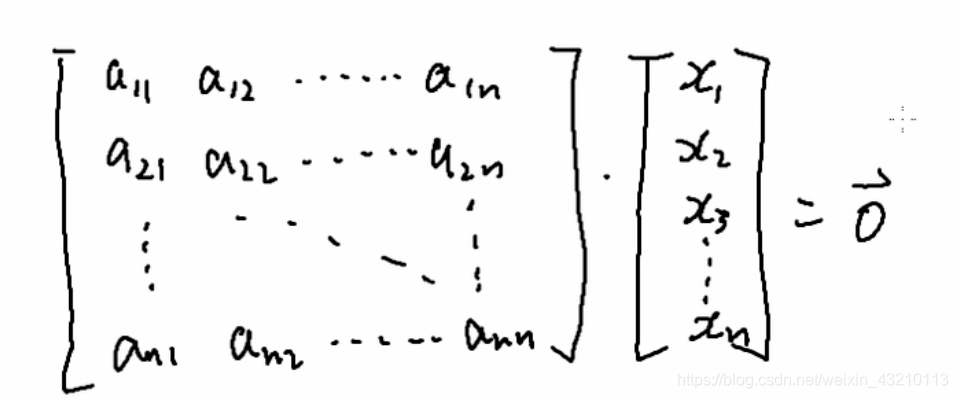
与上面的代数形式含义相同
D为系数矩阵 左边
定理
有非零解 则系数行列式一定为零|D|=0
与|A-λE|=0 相同
(A-λE)X=0
X为非零解,则只能是系数的行列式为0。
P3 03-代数余子式求和
笔记

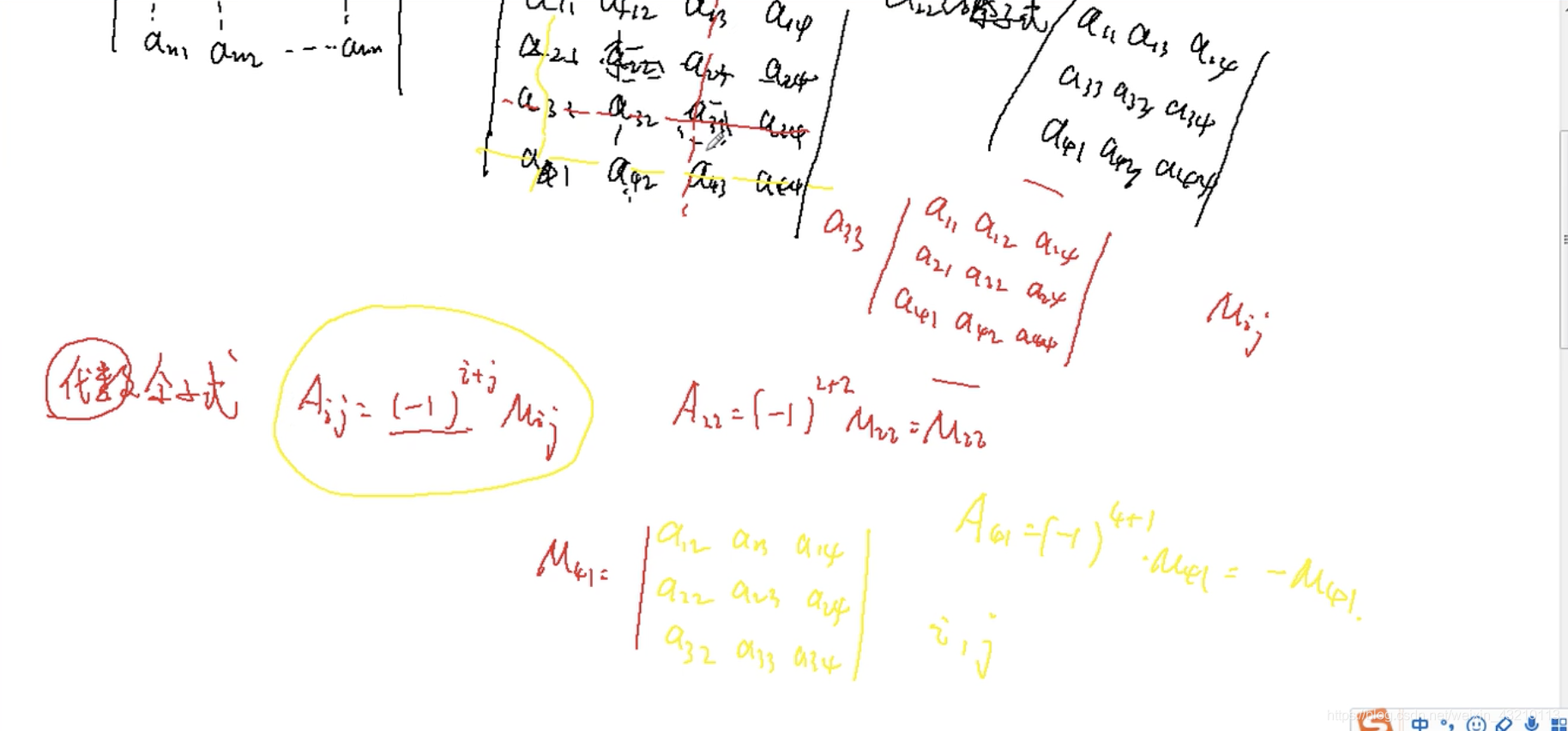
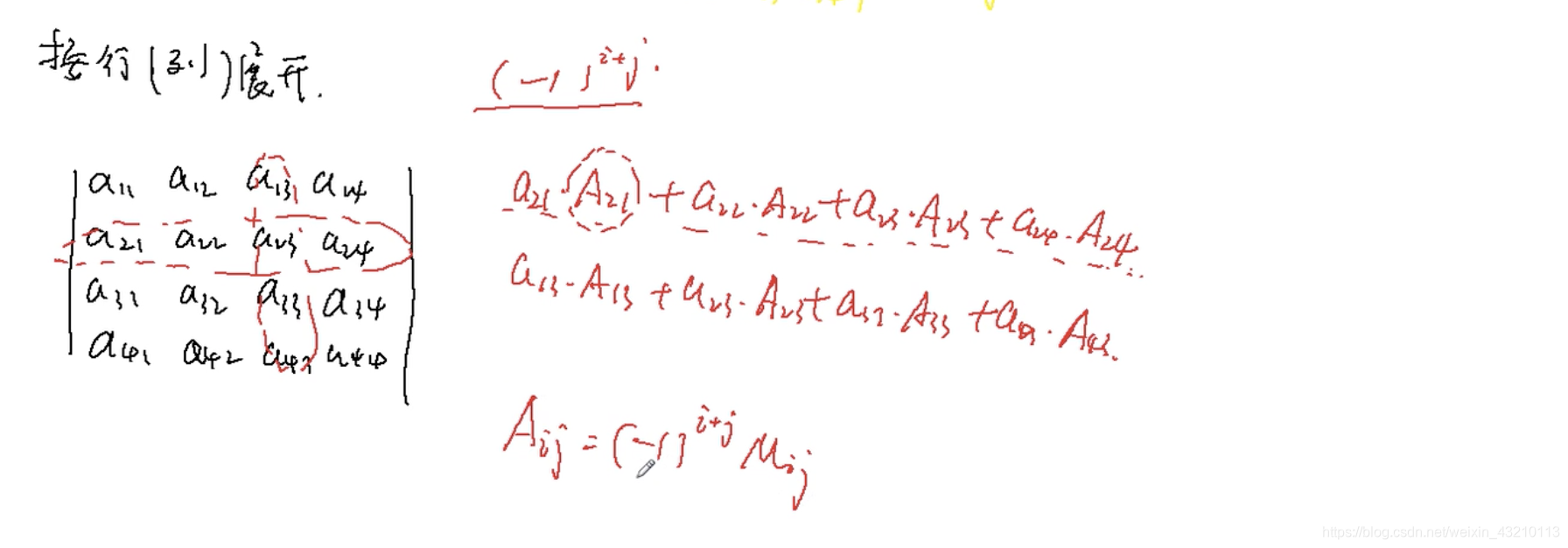
余子式
Dn= |a11 a12 …… a1n|
|a21 a22 …… a2n|
|a31 a32 …… a3n|
|…… …… …… …… |
|an1 an2 …… ann|
任意一个元素aij,划去aij所在的第i行第j列,剩下n-1阶行列式 即余子式
余子式例子
a22 划去第2行第2列
a33划去第3行第3列
代数余子式
记余子式为Mij
代数余子式为Aij=(-1)^(i+j)*Mij
代数余子式例子
要考虑正负号
A22=(-1)^4M22=M22
A41=(-1)^5M41=-M41
应用
按行(列)展开,求得行列式的值
P4 04-3阶行列式计算公式
笔记
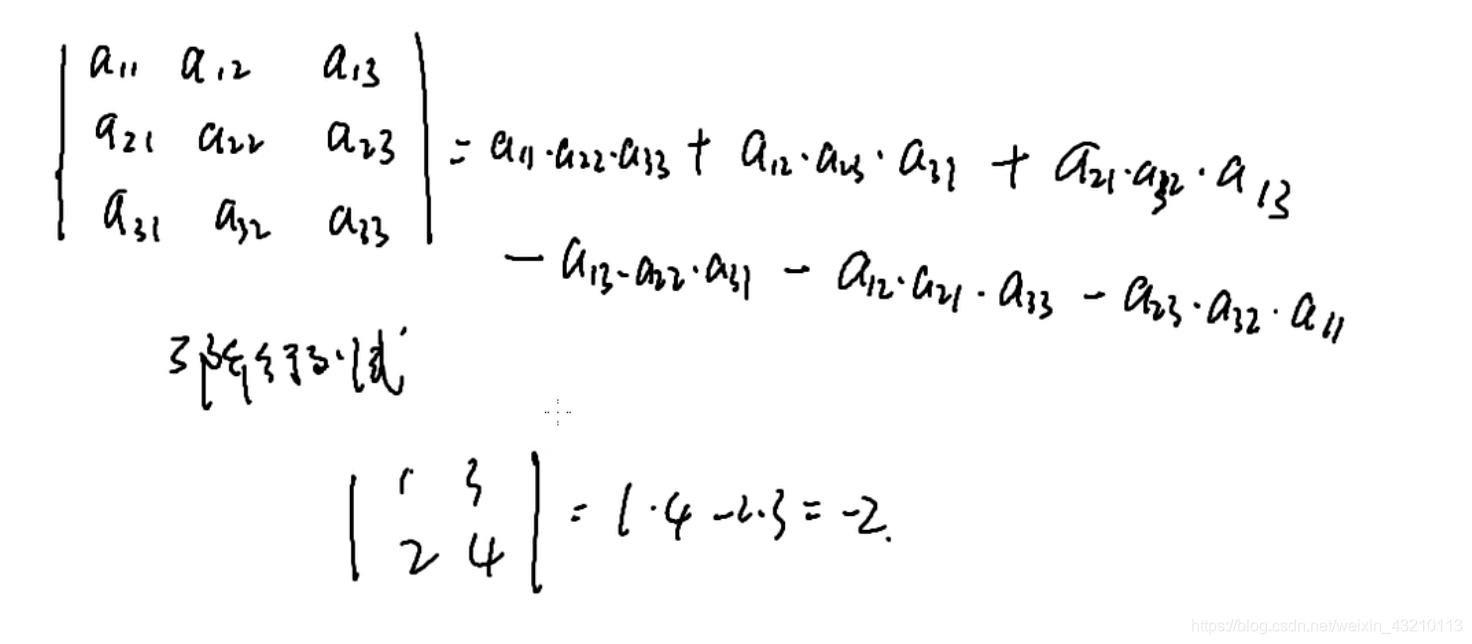
3阶行列式计算公式
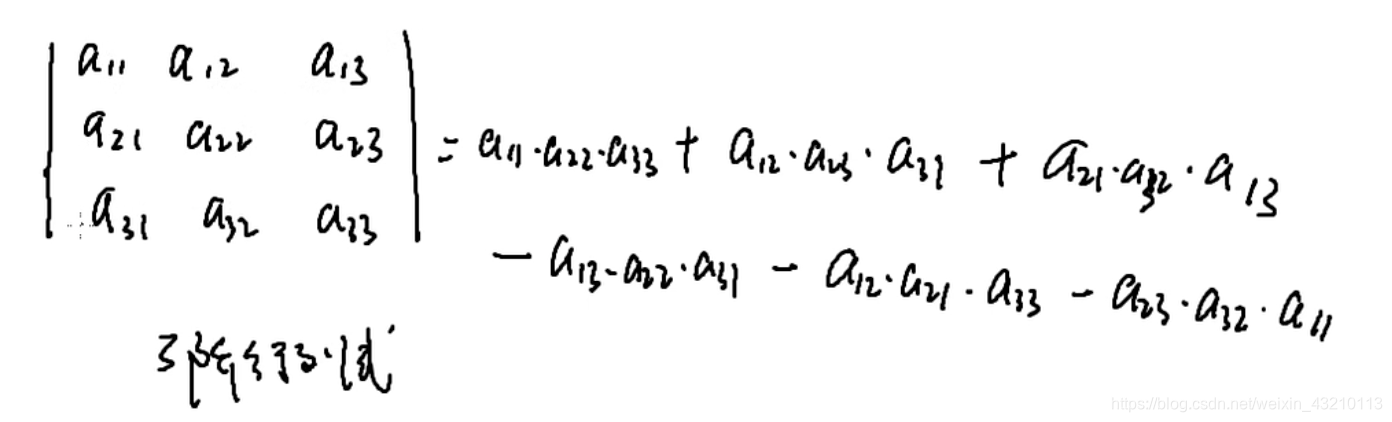
帮助
工作中不会用到
比初等变换更容易
P5 05-求解特征值和特征向量-例题1
笔记
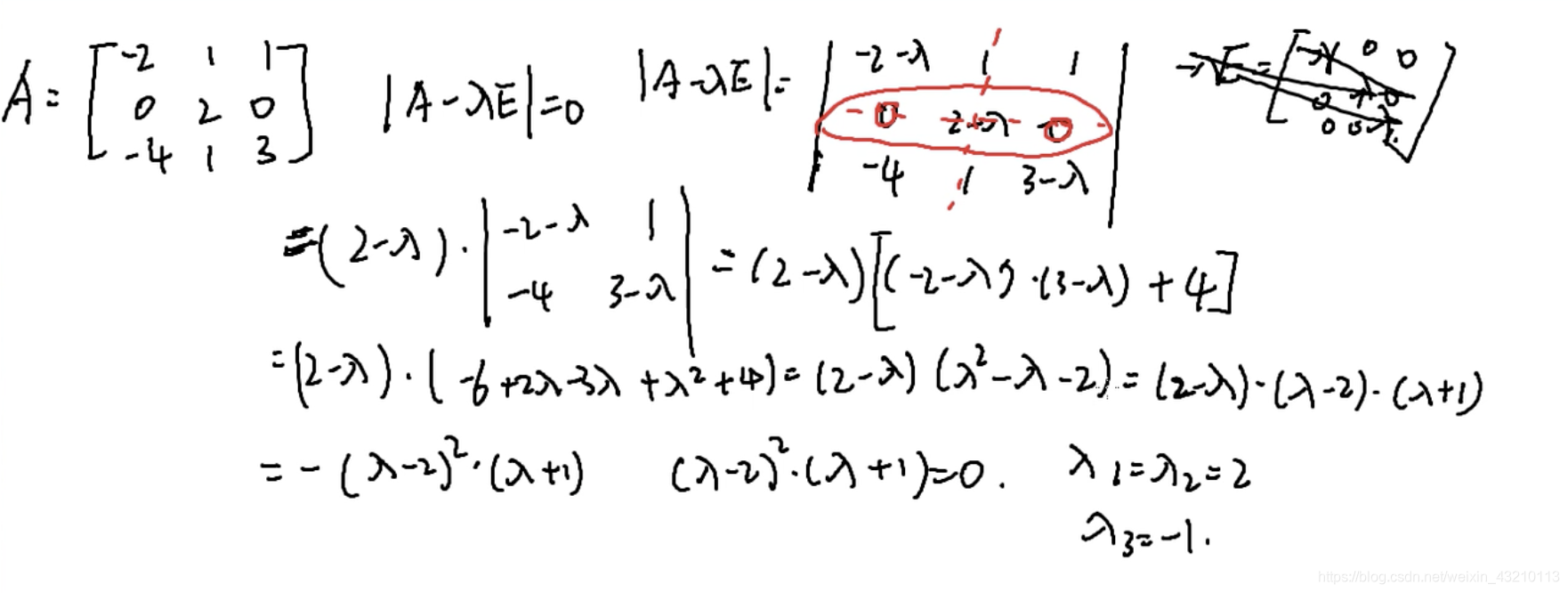

题目
求A的特征值和特征向量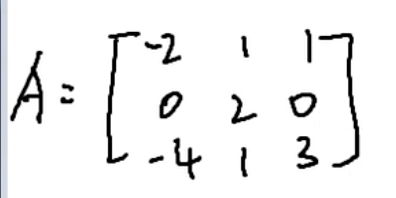
公式
|A-λE|=0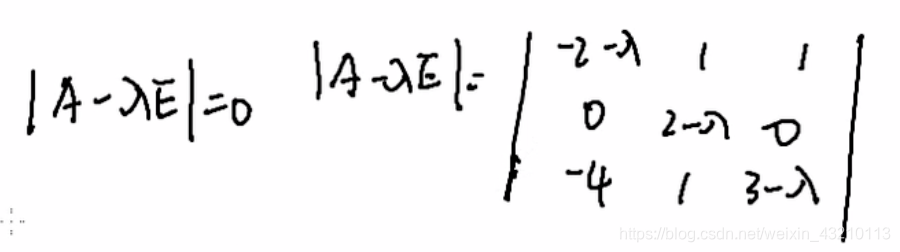
使用第二行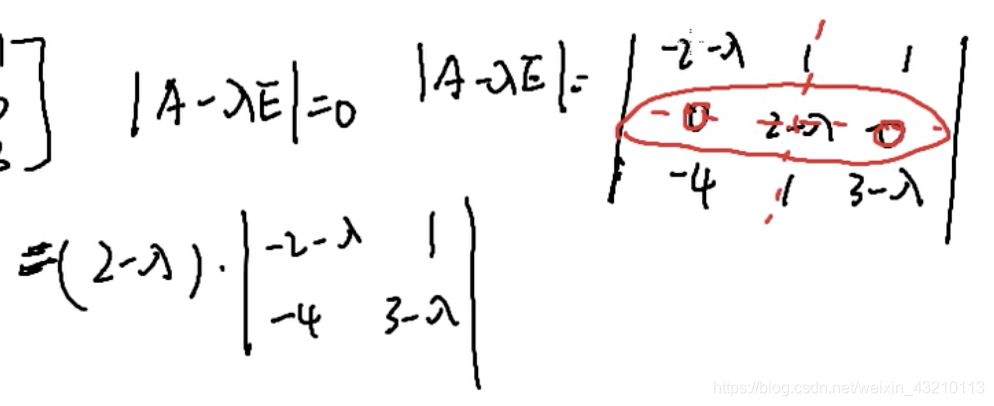
特征值
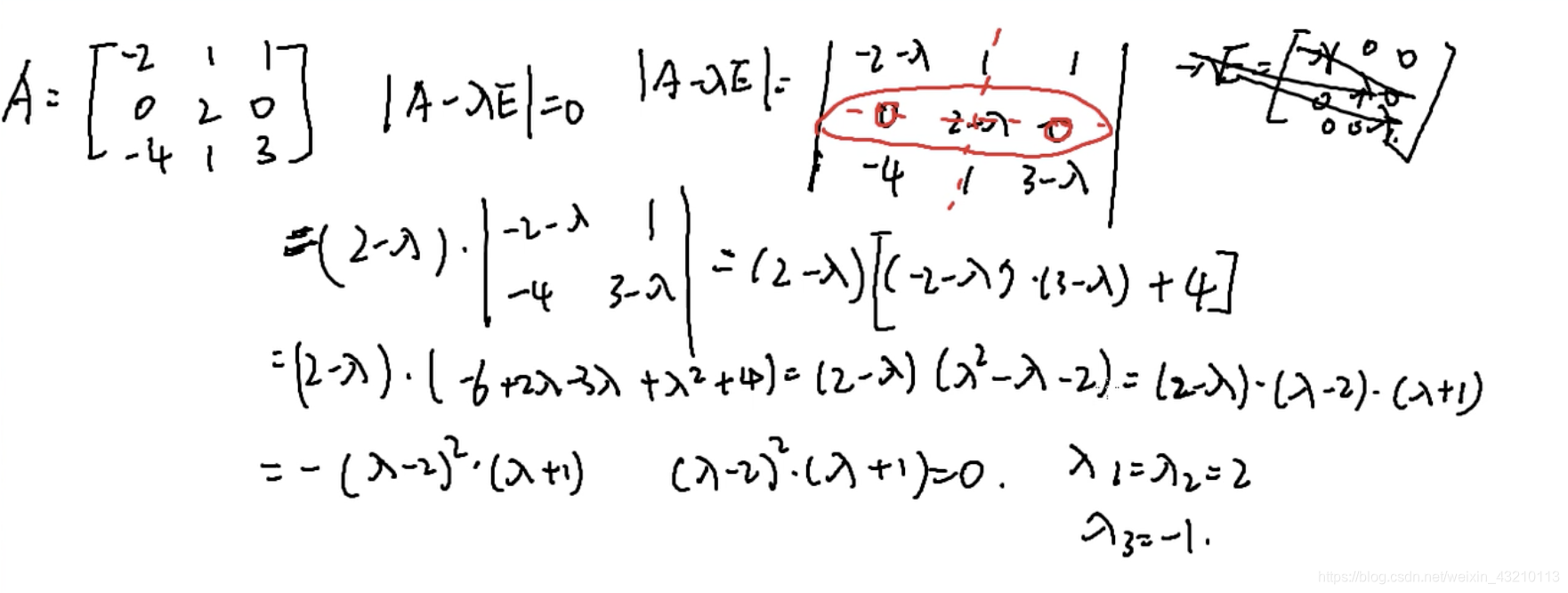
特征向量①λ1=λ2=2时
①λ1=λ2=2时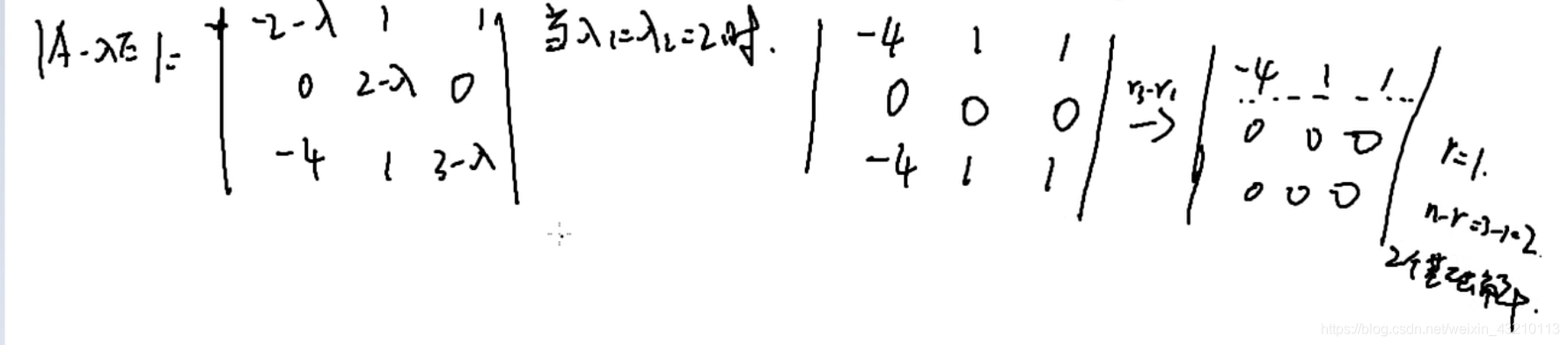
秩 r=1
n-r=3-1=2 有两个基础解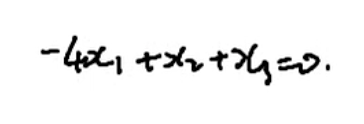
三个未知数 一个方程式 -> 两个自由度
凑特征向量
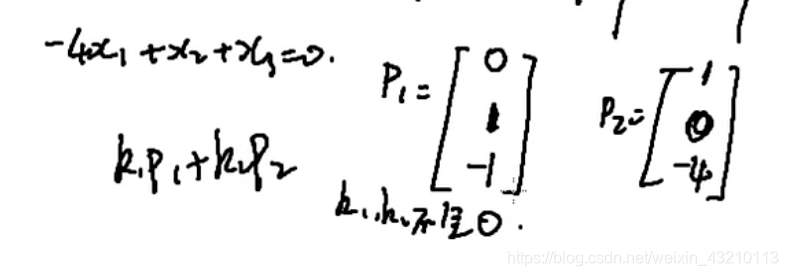
特征向量②λ3=-1时
②λ3=-1时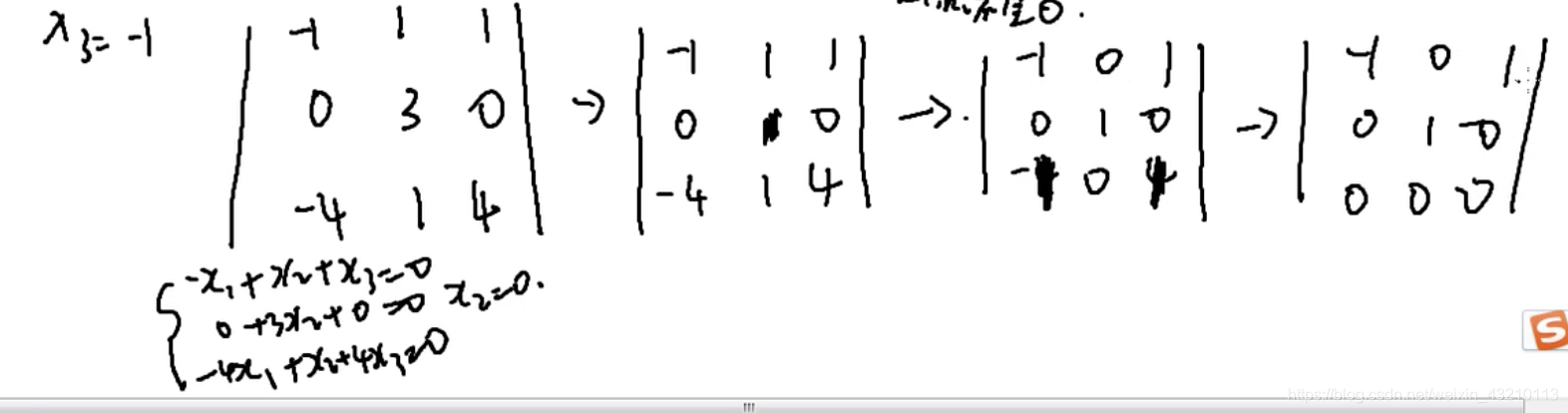
秩 r=2
n-r=3-2=1 有一个基础解
凑特征向量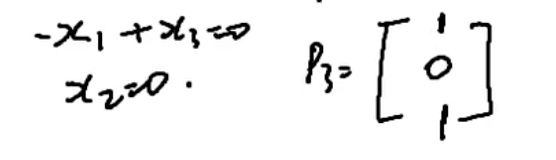
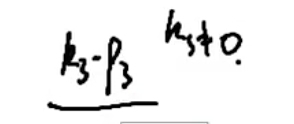
P6 06-求解特征值和特征向量-例题2
笔记
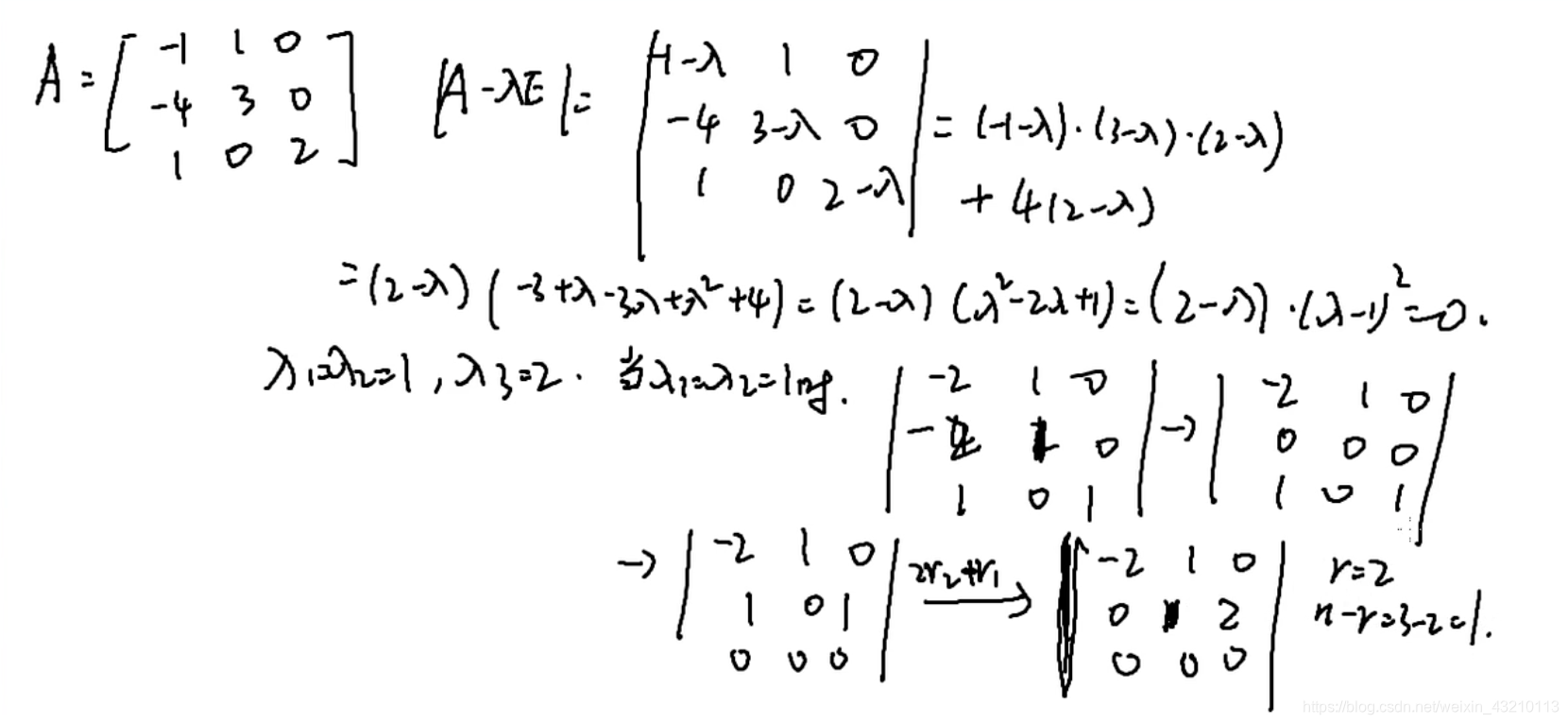

题目
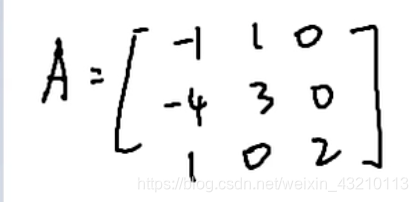
公式(三阶行列式)
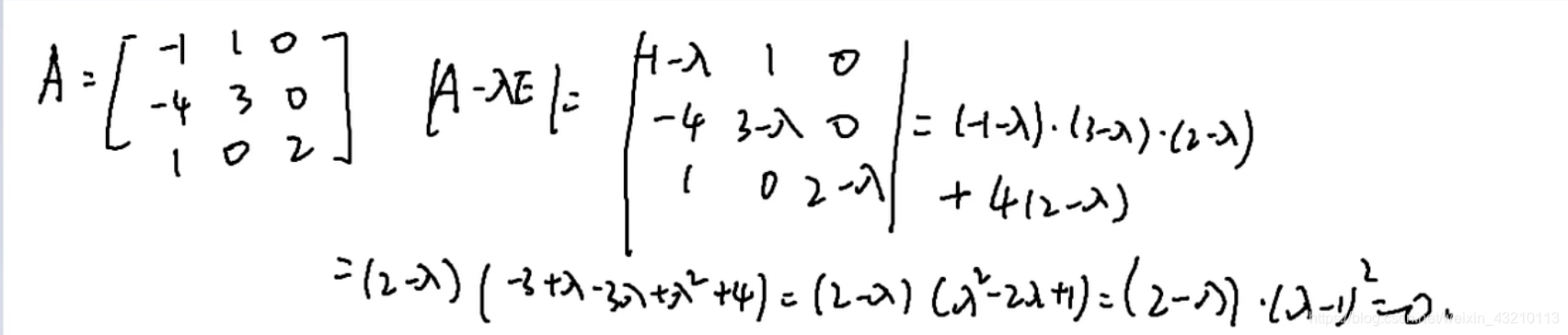
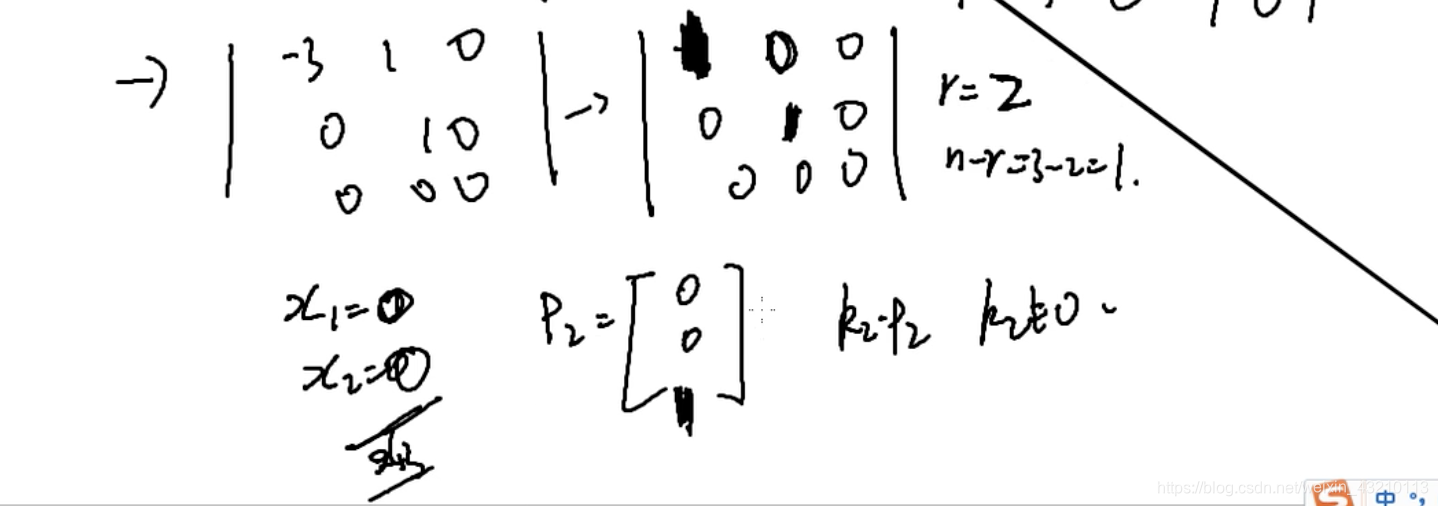
特征向量①λ1=λ2=时
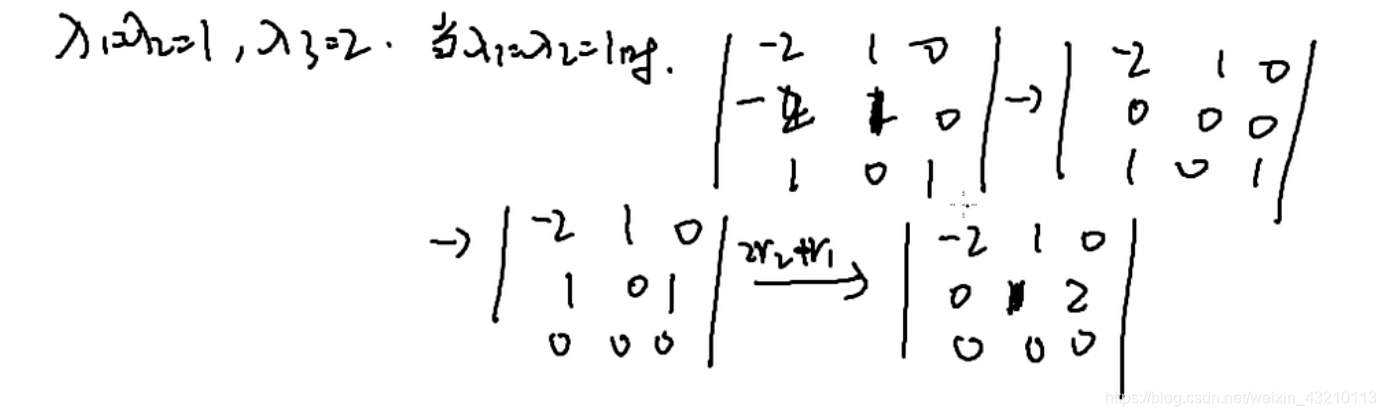
秩r=2
n-r=3-2=1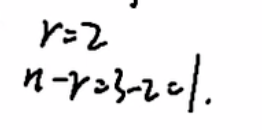
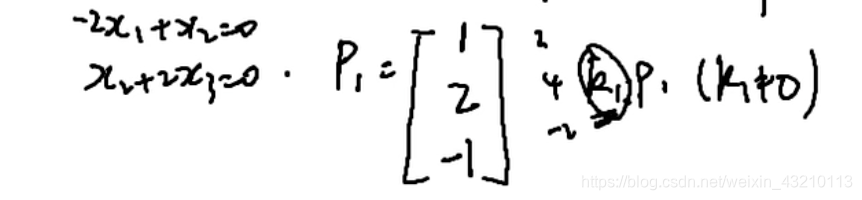
特征向量②λ3=2时
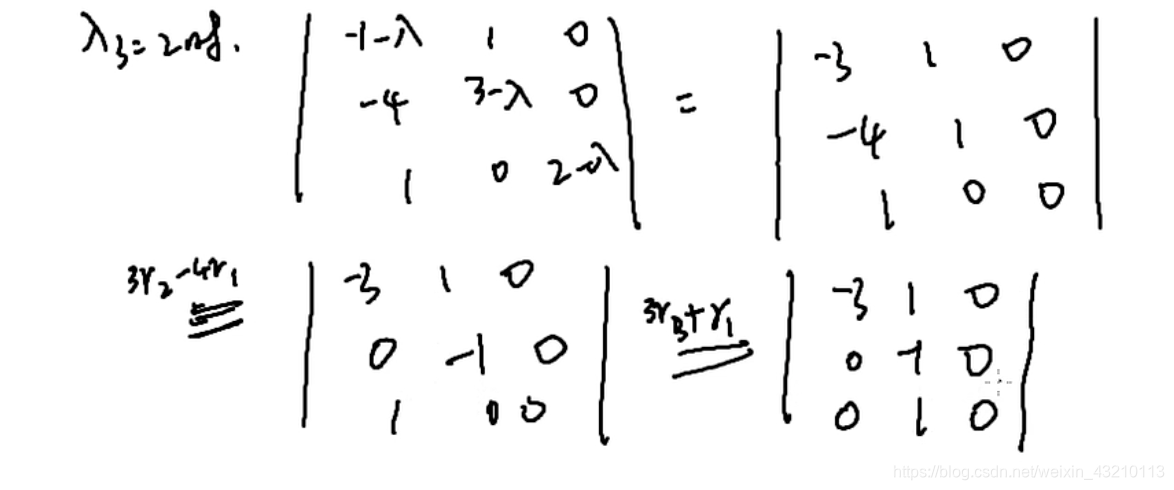
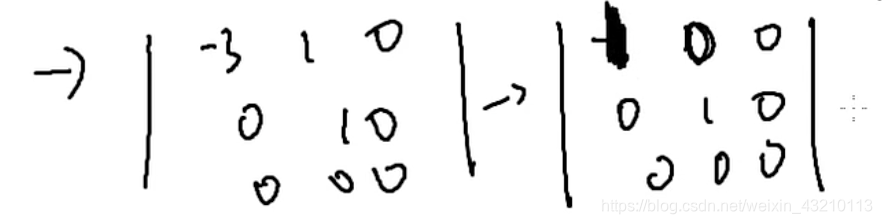
秩r=2
n-r=3-2=1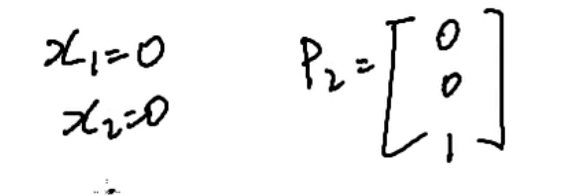
更多推荐
 已为社区贡献2条内容
已为社区贡献2条内容










所有评论(0)