【机器学习】主成分分析(PCA)
本文系统介绍了主成分分析(PCA)这一经典的无监督线性降维技术。首先阐述了PCA的核心目标:降维、特征提取、去相关、噪声过滤和数据可视化。然后详细讲解了PCA的数学基础,包括方差、协方差、协方差矩阵、特征值与特征向量等概念和完整的算法步骤:数据标准化→计算协方差矩阵→特征分解→排序并选择主成分→构建投影矩阵→数据降维。文章对比了PCA的不同变体的优缺点和适用场景,并通过Python代码实现了数据生
目录
五、主成分分析(PCA)实战的算法步骤及Python代码实现
一、引言
在解决复杂的聚类问题时,我们会先用一些手段提取数据的有用特征。对高维复杂数据来说,其不同的维度所代表的特征可能存在关联,还有可能存在无意义的噪声干扰。因此,无论后续任务是监督学习还是无监督学习,我们都希望能先从中提取出具有代表性、能最大限度地保留数据本身信息的几个特征,从而降低数据维度,简化之后的分析和计算。这一过程通常称为数据降维,这同样是无监督学习的重要问题。因此在本文中将要介绍数据降维中最经典的算法——主成分分析(Principal Component Analysis,PCA)。
二、PCA的目标与核心思想
(一)主成分分析 (Principal Component Analysis, PCA) 是一种广泛应用的无监督线性降维技术。其主要目标是:
1. 降维 (Dimensionality Reduction):将高维数据集转换为一个低维数据集,同时尽可能多地保留原始数据的变异信息(方差)。
2. 特征提取 (Feature Extraction):通过原始特征的线性组合,创建一组新的、不相关的特征,称为主成分 (Principal Components, PCs)。这些新特征能够更好地概括数据的主要结构。
3. 去相关 (Decorrelation):生成的主成分是相互正交(不相关)的。
4. 噪声过滤 (Noise Filtering):通常假设方差较小的主成分可能对应于数据中的噪声,通过舍弃这些成分可以达到一定的去噪效果。
5. 数据可视化 (Data Visualization):通过将数据降至2维或3维,可以方便地进行可视化。
(二)核心思想:PCA 试图找到数据中方差最大的方向。第一个主成分 (PC1) 是数据方差最大的方向;第二个主成分 (PC2) 是与PC1正交(垂直)且方差次大的方向;以此类推。
(三)直观理解
想象一个三维空间中的点云(数据集)。如果这些点大致分布在一个扁平的椭球体上,PCA会找到这个椭球体的最长轴作为PC1。这个方向是数据点散布最开的方向。然后,在与PC1垂直的平面内,找到数据散布最开的下一个方向作为PC2(椭球体的次长轴)。对于三维数据,PC3将是与PC1和PC2都垂直的方向(椭球体的最短轴)。通过将数据点投影到由最重要的几个主成分(如PC1和PC2)张成的子空间上,我们就能用更少的维度来表示数据,同时保留了数据的主要变化特征。
三、数学基础
(一)PCA 依赖于以下几个关键的数学概念:
1. 方差 (Variance):衡量单个变量(特征)数据的离散程度。
Var(X) = σ² = Σ(xᵢ - μ)² / (N-1)
2. 协方差 (Covariance):衡量两个变量(特征)之间的线性相关性程度和方向。
Cov(X,Y) = Σ((xᵢ - μₓ)(yᵢ - μᵧ)) / (N-1)
(1)正协方差:两个变量同向变化。
(2)负协方差:两个变量反向变化。
(3) 零协方差:两个变量线性不相关。
3. 协方差矩阵 (Covariance Matrix, Σ):对于一个包含 d 个特征的数据集,协方差矩阵是一个 d x d 的对称矩阵。其对角线元素是各个特征的方差,非对角线元素是特征对之间的协方差。
4. 特征值与特征向量 (Eigenvalues and Eigenvectors):对于一个方阵 A,如果存在一个非零向量 v 和一个标量 λ 使得 Av = λv,则 λ 称为特征值,v 称为对应于 λ 的特征向量。
(1)在PCA中,协方差矩阵的特征向量指出了主成分的方向。
(2)协方差矩阵的特征值表示数据在对应特征向量(主成分)方向上的方差大小。特征值越大,说明该主成分包含的原始数据信息越多。
四、PCA算法的完整步骤
(一)假设我们有一个数据集 X,包含 n 个样本和 d 个特征。
步骤 1:数据标准化(Standardization)
目的:PCA对特征的尺度非常敏感。如果不同特征的尺度差异很大,尺度较大的特征会在计算方差时占据主导地位,导致PCA结果偏向这些特征。标准化使得所有特征具有相同的贡献权重。
操作:对每一个特征(数据集的每一列),减去其均值并除以其标准差。
X_std_ij = (X_ij - μ_j) / σ_j
其中 μ_j 是第 j 个特征的均值,σ_j 是第 j 个特征的标准差。
标准化后的数据 X_std 的每个特征均值为0,标准差为1。
步骤 2:计算协方差矩阵 (Σ)
目的:协方差矩阵描述了数据中不同特征之间的线性关系以及各个特征自身的变异程度。
操作:使用标准化后的数据 X_std 计算协方差矩阵。
Σ = (1 / (n - 1)) * X_stdᵀ @ X_std
其中 n 是样本数量,X_stdᵀ 是 X_std 的转置。
结果是一个 d x d 的对称矩阵。
步骤 3:计算协方差矩阵的特征值和特征向量
目的:找到数据变化的主要方向(由特征向量给出)以及这些方向上的变化幅度(由特征值给出)。
操作:对协方差矩阵 Σ 进行特征分解。
Σv = λv
求解得到 d 个特征值 λ₁, λ₂, ..., λd 和对应的 d 个特征向量 v₁, v₂, ..., vd。每个特征向量 vᵢ 的维度是 d x 1。
步骤 4:对特征值和特征向量进行排序
目的:确定主成分的重要性。
操作:将特征值从大到小排序:λ₁ ≥ λ₂ ≥ ... ≥ λd。
同时,按照特征值的大小顺序重新排列对应的特征向量。
排序后,与最大特征值 λ₁ 对应的特征向量 v₁ 就是第一主成分 (PC1) 的方向。
与第二大特征值 λ₂ 对应的特征向量 v₂ 就是第二主成分 (PC2) 的方向,以此类推。
这些特征向量(主成分方向)是相互正交的。
步骤 5:选择主成分的数量 (k)
目的:确定要保留的维度数量,以在降维和信息保留之间取得平衡。
操作**:选择前 `k` 个主成分,其中 `k < d`。选择 `k` 的常用方法有:
1. 解释方差比例 (Explained Variance Ratio):计算每个主成分解释的方差占总方差的比例 (λᵢ / Σλⱼ),然后计算累积解释方差比例。选择一个 k,使得累积解释方差达到一个预设的阈值(例如,保留90%、95%或99%的方差)。
2. 碎石图 (Scree Plot):将排序后的特征值绘制成图表。通常在特征值急剧下降之后趋于平缓的地方(肘部)选择 k。肘部之后的特征值通常较小,可能对应噪声或不太重要的变化。
3. 根据应用需求:例如,如果目标是可视化,通常选择 k=1 或 k=2 或 k=3。
步骤 6:构建投影矩阵 (W)
目的:创建一个矩阵,用于将原始数据投影到选定的主成分子空间。
操作:选择在前一步中确定的前 k 个特征向量 v₁, v₂, ..., vk。
将这 k 个特征向量作为列向量,构建一个 d x k 的投影矩阵 W。
W = [v₁ | v₂ | ... | vk]
步骤 7:投影数据到新的低维子空间
目的:得到降维后的数据集。
操作:将标准化后的原始数据 X_std (一个 n x d矩阵) 乘以投影矩阵 W。
X_pca = X_std @ W
得到的结果 X_pca 是一个 n x k 的矩阵。X_pca的每一行是原始数据中对应样本在新主成分空间中的坐标,每一列对应一个主成分的得分。
(二)解释PCA结果
1.. 主成分 (Principal Components):是原始特征的线性组合,代表数据中方差最大的方向。它们是相互正交的。
2. 载荷 (Loadings):投影矩阵 W 中的元素(即特征向量的元素)称为载荷。第 j 个原始特征在第 i 个主成分上的载荷,表示该原始特征对构成这个主成分的贡献程度和方向。载荷的绝对值越大,说明该原始特征对该主成分越重要。
3. 得分 (Scores):降维后的数据 X_pca 中的值称为得分。每个样本在每个主成分上的得分,表示该样本在该主成分方向上的位置。
4. 解释方差 (Explained Variance):每个特征值 λᵢ 代表对应主成分 PCᵢ 所解释的方差量。解释方差比例 (λᵢ / Σλⱼ) 更直观地表示了每个PC的重要性。
(三)PCA的假设与局限性
1. 线性假设:PCA假设数据的主要变化方向是线性的。如果数据结构是非线性的,PCA可能无法有效捕捉。
2. 方差越大越重要:PCA假设方差最大的方向是最重要的。在某些情况下,方差较小的方向可能包含对特定任务(如分类)更重要的信息。
3. 均值和方差足以描述数据:PCA依赖于数据的二阶统计量(均值和协方差)。对于非高斯分布的数据,这可能不是最佳选择。
4. 对数据缩放敏感:如前所述,需要进行数据标准化。
5. 主成分的解释性:虽然主成分在数学上是最优的,但它们是原始特征的混合,有时可能难以赋予直观的物理解释。
6. 信息损失:降维必然会导致一部分信息损失,尤其是当舍弃的主成分仍包含一些有用信息时。
(四)PCA的优点
1. 简单高效:算法基于线性代数,计算相对简单。
2. 无参数调整(除了k):除了选择主成分数量 k 外,没有其他超参数需要调整。
3. 去相关性:生成的主成分相互正交,消除了原始特征间的线性相关性,这对于某些后续的机器学习算法是有益的。
4. 有效降维:能显著减少数据维度,同时保留大部分信息。
5. 可视化:是高维数据可视化的有力工具。
(五)PCA的缺点
1. 线性限制:不能很好地处理非线性数据结构(此时可以考虑核PCA等非线性降维方法)。
2. 可能丢失重要信息:如果重要信息存在于方差较小的方向,PCA可能会将其舍弃。
3. 对异常值敏感:异常值可能显著影响均值和协方差的计算,从而影响主成分的方向。
4. 解释性可能较差:主成分是原始特征的组合,其物理意义可能不明确。
(六)PCA的应用场景
1.数据压缩与降维:减少存储需求和计算复杂度。
2.特征工程:作为机器学习模型的预处理步骤,生成新的特征集。
3.数据可视化:将高维数据投影到2D或3D空间进行观察。
4.噪声消除:通过去除方差较小的主成分来过滤噪声。
5.图像处理:如人脸识别中的“特征脸”(Eigenfaces)。
6.生物信息学:如基因表达数据分析。
7.金融领域:如风险因子分析。
五、主成分分析(PCA)实战的算法步骤及Python代码实现
(一)主成分分析(PCA)实战的算法步骤
1.核心目标:这份代码旨在全面探索和比较主成分分析 (PCA) 及其多种变体(稀疏PCA, 核PCA, 增量PCA)在不同类型数据集上的表现。它通过可视化和量化指标(如解释方差、重构误差、计算时间、稀疏度)来评估这些降维技术。
2.整体代码结构:
(1) 环境设置:
a.导入必要的库 (numpy, matplotlib, pandas, sklearn.decomposition, sklearn.datasets, time, os, shutil)。
b.设置 matplotlib 以支持中文显示(如果配置了中文字体)。
c.创建一个目录 (pca_analysis_images) 用于保存生成的图像。
(2) 数据集生成与加载 (函数 generate_pca_friendly_dataset 和第2部分):
a.目的:提供一个可控的合成数据集,其中包含明确的强主成分和噪声,便于验证PCA的效果。
b.步骤:
(a)定义样本数 (n_samples)、原始特征数 (n_features)、强主成分数 (n_components_strong)。
(b) 生成一个随机正交基 (q_strong) 作为强主成分的真实方向(载荷)。
(c)生成服从高斯分布的得分(scores),并乘以指定的方差 (strong_component_variance_val),然后通过真实载荷投影回原始特征空间,构成数据的主要结构部分。
c.数学上:Data_strong = Scores_strong @ Loadings_true^T
d. (可选)类似地生成弱主成分部分,其方向与强主成分正交,方差较小 (weak_component_variance_val)。
e. 添加高斯噪声 (noise_std)。
f. (可选)添加一个随机的均值偏移。
g. 将生成的数据保存为CSV文件 (pca_synthetic_data_for_report.csv)。
(a)数据加载:脚本首先尝试从CSV文件加载数据;如果文件不存在,则调用 generate_pca_friendly_dataset 生成新的数据。
(b)数据中心化:对加载或生成的数据进行中心化处理,即每个特征减去其均值。这是PCA的标准预处理步骤。
(c)X_centered = X - mean(X) (按列计算均值)
(3) 标准PCA分析 (第3部分):
a.核心思想:找到数据中方差最大的方向(主成分),将数据投影到这些方向上以实现降维,同时保留尽可能多的原始信息(方差)。
b.数学步骤:
(a) 计算中心化数据 X_centered 的协方差矩阵 Σ:
Σ = (1 / (n_samples - 1)) * X_centered^T @ X_centered
(b)对协方差矩阵 Σ 进行特征值分解:
ΣV = VΛ
其中 V 是特征向量矩阵(其列向量是主成分方向/载荷),Λ 是对角矩阵,对角线元素是特征值(表示对应主成分的方差)。
(c) 按特征值大小降序排列特征向量。选择前 k 个特征向量构成投影矩阵 W (k x d, d是原始特征数)。
(d) 将数据投影到新的低维空间:
X_pca = X_centered @ W^T
c.代码实现 (sklearn.decomposition.PCA):
(a) pca_model_full = PCA(n_components=n_features_original):初始化PCA模型,保留所有主成分以分析其完整谱。
(b) pca_model_full.fit(data_centered):执行上述数学步骤(计算协方差、特征分解等)。
(c) explained_variance_ratio_:获取每个主成分解释的方差比例(特征值 / 总特征值之和)。
(d) cumulative_explained_variance:计算累积解释方差比。
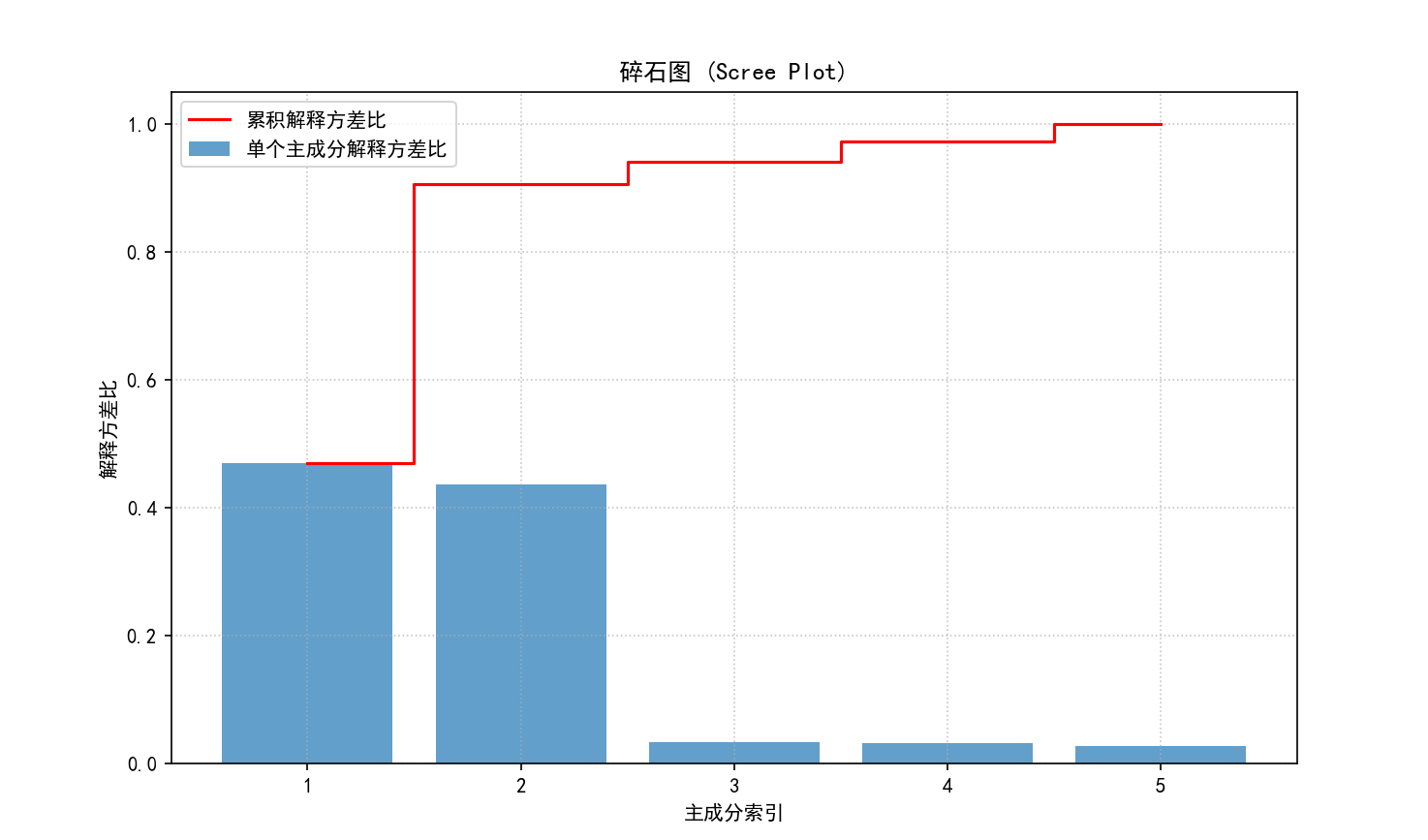
( e) 碎石图 (Scree Plot):可视化每个主成分的解释方差比和累积解释方差比。这有助于决定保留多少主成分。
保存图像为 01_scree_plot.png。
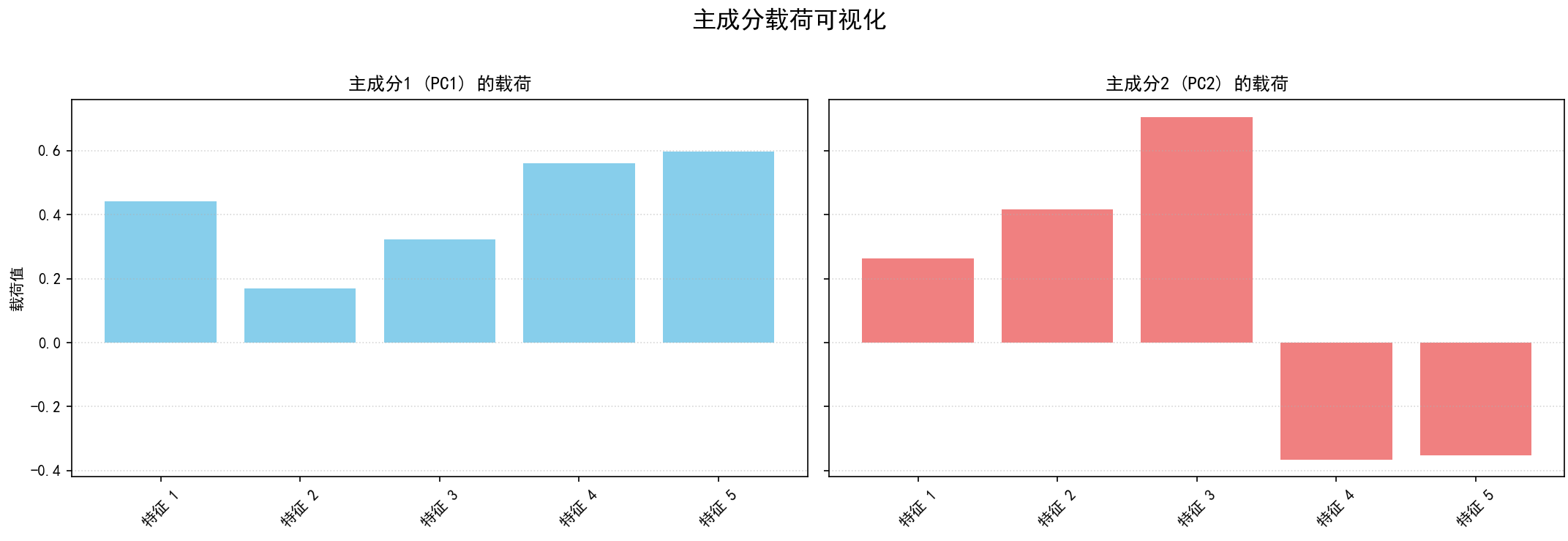
(f)主成分载荷可视化:如果特征数大于等于2,可视化前两个主成分的载荷(特征向量的元素)。载荷表示原始特征对主成分的贡献程度。
保存图像为 02_pca_loadings.png。
(4) “交互式”PCA图的静态演示 (函数 static_pca_plot_demonstration 和第4部分):
a.目的:模拟选择不同数量主成分 (k) 时,数据的2D投影(通常是PC1 vs PC2)和碎石图的变化。
b.步骤:
(a)使用 pca_model_full.transform(data_centered) 获得所有主成分上的投影 X_pca_full。
(b)对于预设的几个 `k` 值(例如1, 2, 3):
PCA投影图:
如果 k=1,绘制第一主成分的直方图。
如果 k>=2,绘制前两个主成分(PC1, PC2)的散点图,点按PC1的值着色。
碎石图:与标准PCA分析中的碎石图类似,但会高亮显示当前选择的 k 值及其对应的累积解释方差。
(c) 为每个 k 值生成的组合图保存为 03_static_pca_demo_k{k_val}_{idx}.png。
(5) PCA逆变换与重构误差评估 (函数 visualize_pca_reconstruction 和第5部分):
a.目的:评估使用不同数量主成分 k 重构原始数据时的精度。
b.数学步骤 (逆变换):
X_reconstructed = X_pca_k @ W_k + mean(X_original)
其中 X_pca_k 是使用前 k 个主成分降维后的数据,W_k 是由前 k 个主成分载荷组成的矩阵。sklearn 的 inverse_transform 会自动处理均值的加回。
* 步骤:
(a)对于一系列 `k` 值:
使用 PCA(n_components=k) 训练模型并对数据进行降维 (fit_transform)。
使用 inverse_transform 将降维后的数据重构回原始特征空间。
计算均方误差 (MSE):MSE = mean((X_original_centered - X_reconstructed_centered)^2)。
可视化重构对比:随机选择几个样本,绘制它们原始特征值与重构特征值的对比图。
可视化误差分布:绘制每个样本的重构误差范数(||原始 - 重构||)的直方图。
(b) 将上述对比图和误差分布图组合显示,保存为 04_pca_reconstruction_comparison.png。
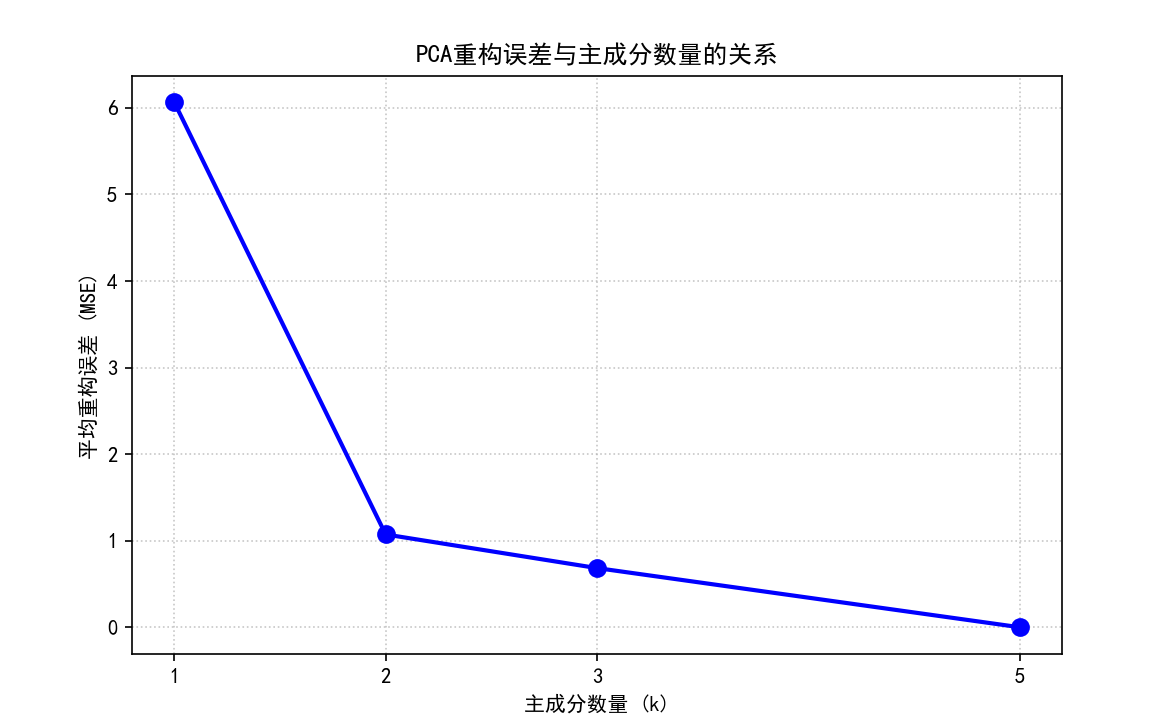
(c) 绘制 MSE 与 k 值的关系曲线图,保存为 05_pca_reconstruction_mse_vs_k.png。
(6) 稀疏PCA (Sparse PCA) (函数 implement_sparse_pca 和第6部分):
a.核心思想:在PCA的基础上引入稀疏性约束,使得主成分的载荷向量中包含许多零元素。这有助于识别对主成分贡献最大的少数几个原始特征,提高模型的可解释性。
b.数学目标 (简化形式,实际优化更复杂):
最小化 ||X - UV^T||_F^2 + α * ||V||_1
其中 U 是降维后的数据 (scores),V 是稀疏载荷矩阵 (components),α 是稀疏度控制参数(L1正则化项的系数)。
c.步骤 (sklearn.decomposition.SparsePCA):
(a) 初始化 SparsePCA(n_components=n_comp, alpha=alpha_val, n_jobs=1)。alpha 控制稀疏程度,n_jobs=1 避免并行化问题。
(b) fit_transform(X_cent) 学习稀疏主成分并转换数据。
(c) 载荷可视化:
将标准PCA的载荷和稀疏PCA的载荷并排用热图 (imshow) 展示,以对比其稀疏性。
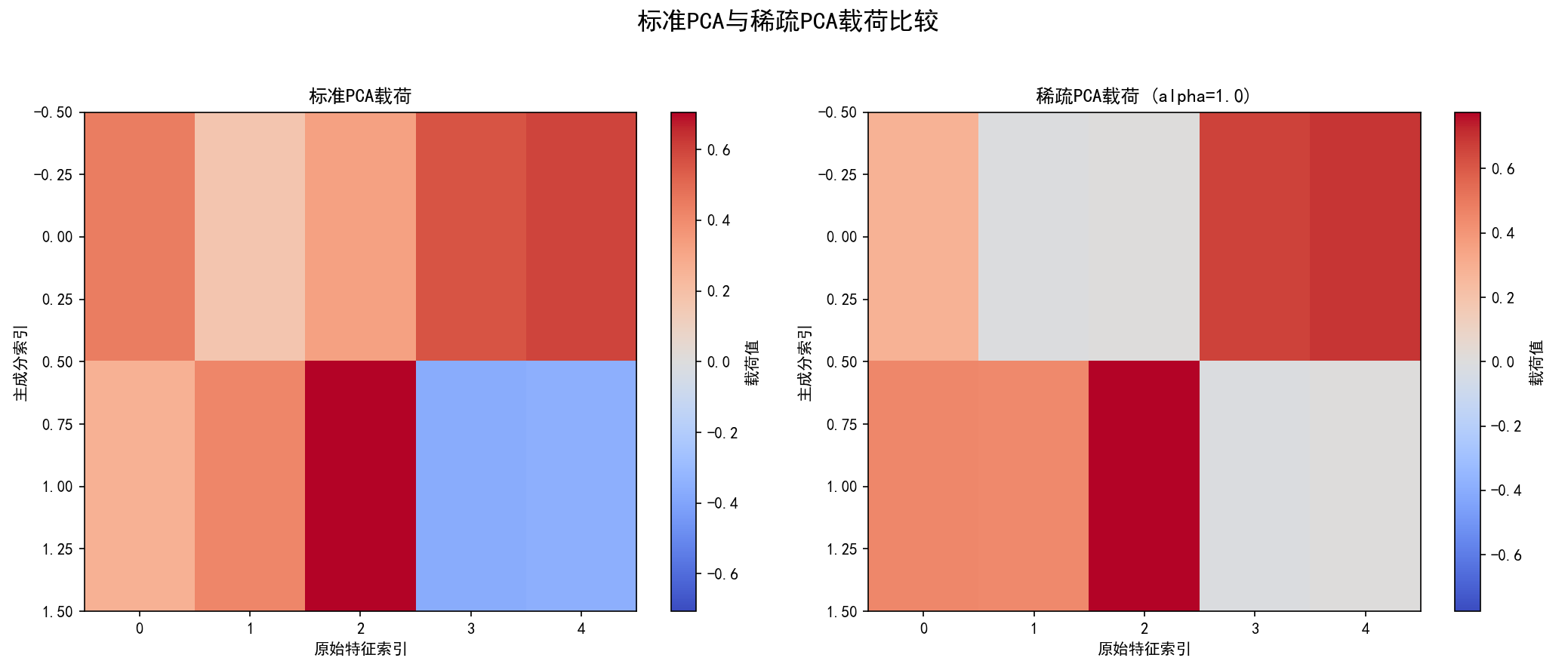
保存图像为 06_sparse_pca_loadings_alpha{alpha_val}.png。
(d) 降维结果可视化:如果 n_comp >= 2,绘制标准PCA和稀疏PCA降维后的前两个主成分的散点图进行比较。
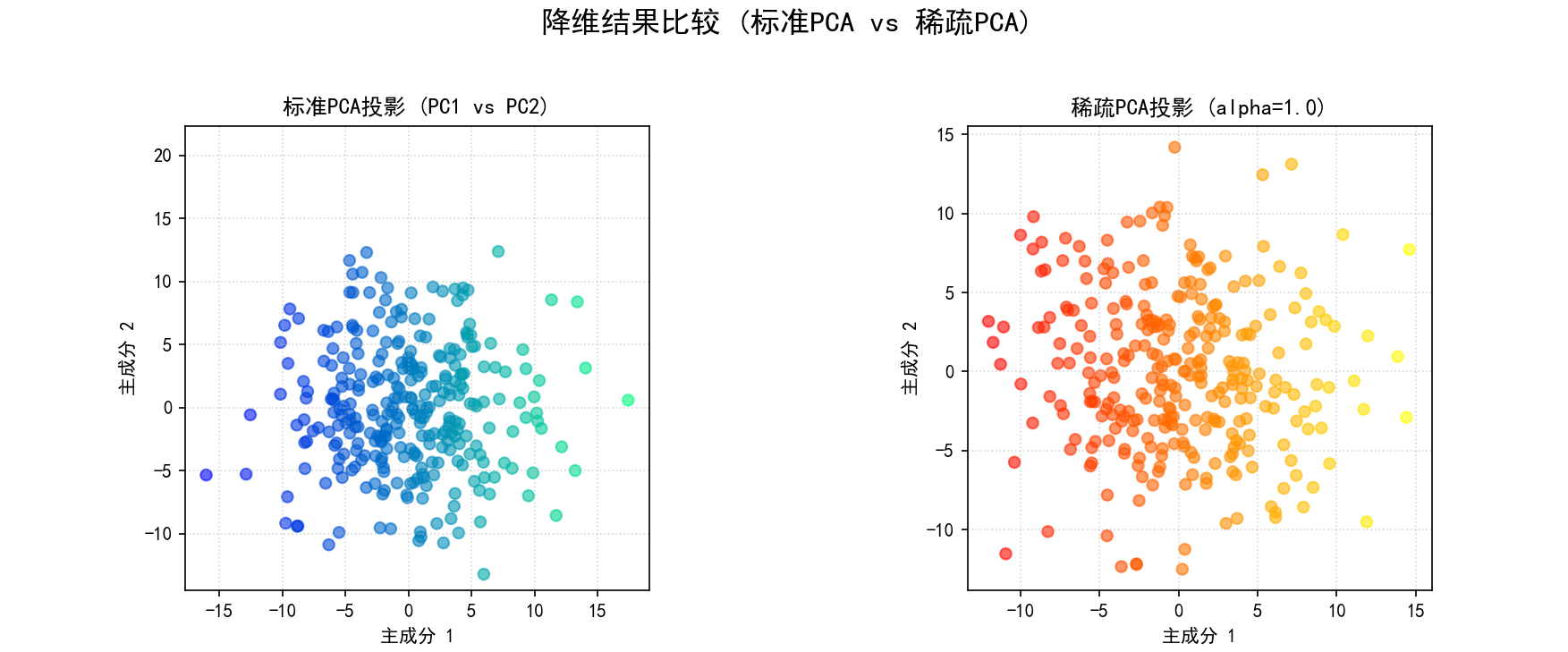
保存图像为 07_sparse_pca_projection_alpha{alpha_val}.png。
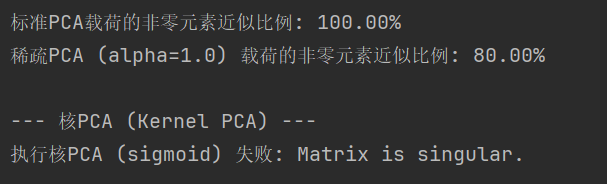
(e) 稀疏度分析:计算并打印标准PCA和稀疏PCA载荷矩阵中非零元素的比例。
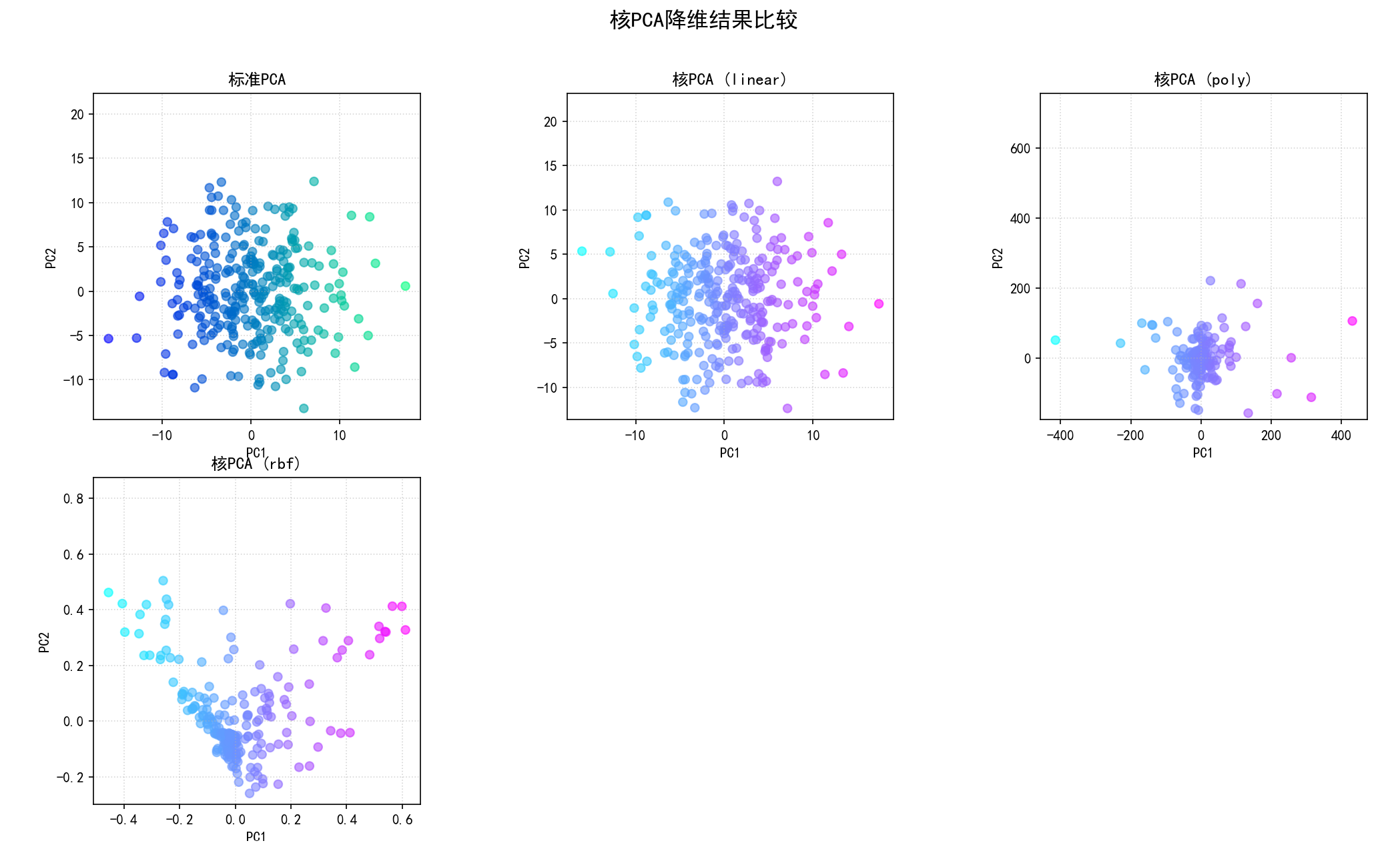
(7) 核PCA (Kernel PCA) (函数 implement_kernel_pca 和第7部分):
a.核心思想:通过核技巧将数据映射到高维特征空间,然后在该高维空间中执行PCA。这使得KPCA能够发现原始特征空间中的非线性结构。
b.数学步骤:
(a)选择一个核函数 κ(x_i, x_j) (如线性核、多项式核、RBF核、Sigmoid核)。
(b) 构建核矩阵 K,其中 K_ij = κ(x_i, x_j)。
(c) 中心化核矩阵 K_centered (在特征空间中中心化)。
(d) 对 K_centered 进行特征值分解:K_centered α = λ α。
(e) 选择前 k 个特征向量 α_1, ..., α_k。
(f) 对于新的数据点 x,其在第 m 个核主成分上的投影是:
projection_m(x) = Σ_i α_m_i * κ(x_i, x)
c.步骤 (sklearn.decomposition.KernelPCA):
(a) 对于不同的核函数 (linear, poly, rbf, sigmoid):
初始化 KernelPCA(n_components=n_comp, kernel=kernel_name, gamma=gamma_val, fit_inverse_transform=True)。fit_inverse_transform=True 允许(近似的)逆变换。
fit_transform(X_cent) 执行KPCA。
(b)降维结果可视化:将标准PCA和各种核PCA降维后的前两个主成分的散点图并排展示。
保存图像为 08_kernel_pca_projections.png。
(c) 重构误差计算:如果可能(fit_inverse_transform=True 且模型支持),计算并打印使用不同核函数重构原始数据时的MSE。
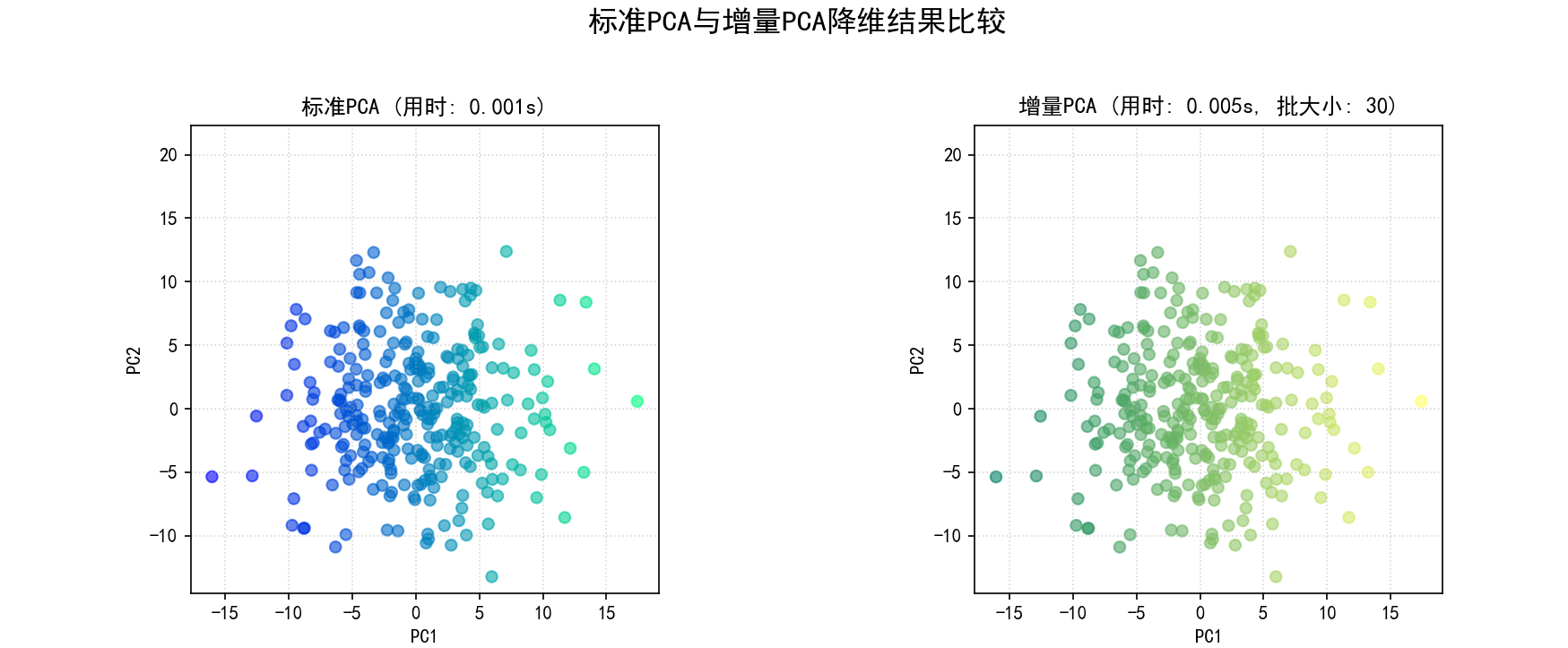
(8) 增量PCA (Incremental PCA) (函数 implement_incremental_pca 和第8部分):
a.核心思想:允许在不加载整个数据集到内存的情况下,分批次地训练PCA模型。适用于非常大的数据集。它通过对数据块进行部分PCA,并结合先前计算的结果来近似完整PCA。
b.步骤 (sklearn.decomposition.IncrementalPCA):
(a) 初始化 IncrementalPCA(n_components=n_comp, batch_size=batch_s)。batch_size 定义每次处理的数据块大小。
(b) fit_transform(X_cent) 分批次处理数据并学习主成分。
(c) 与标准PCA比较:
降维结果可视化:绘制标准PCA和增量PCA降维后的前两个主成分的散点图,并标注计算时间。
保存图像为 09_incremental_pca_comparison.png。
解释方差比比较:打印两者的解释方差比。
主成分相似性:计算两者主成分向量的点积(余弦相似度的近似)。
重构误差比较:计算并打印两者的MSE。
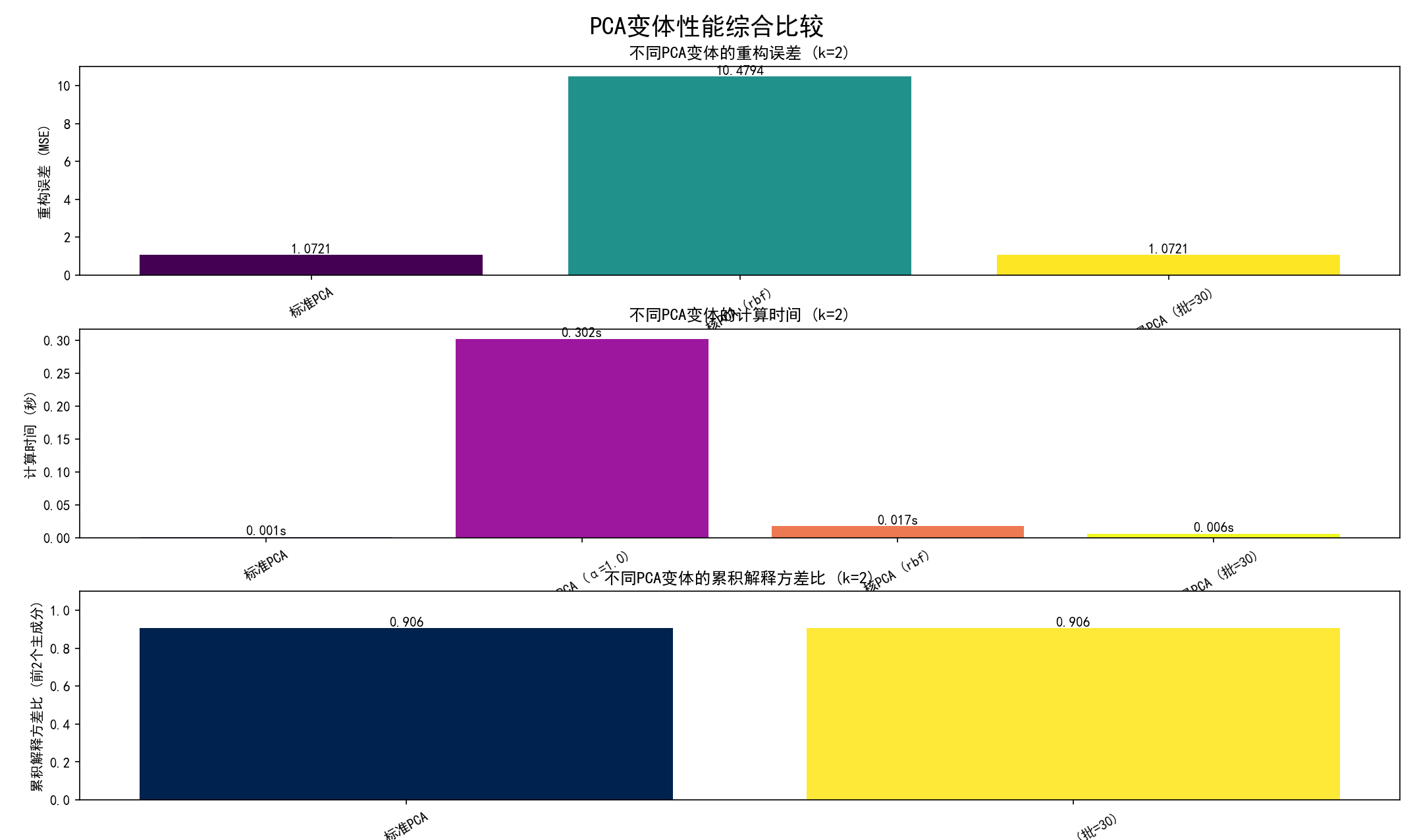
(9) 全面比较PCA变体 (函数 compare_all_pca_variants 和第9部分):
a.目的:在一个统一的框架下,对比标准PCA、稀疏PCA、核PCA(如果数据集不大)和增量PCA在关键指标上的表现。
b.步骤:
(a) 对中心化后的数据,依次应用上述四种PCA变体(稀疏PCA使用固定alpha,核PCA使用RBF核,增量PCA使用自动确定的批大小)。
(b) 为每种方法记录:
计算时间。
(近似的)累积解释方差比(如果可用)。
重构误差(如果可用)。
对于稀疏PCA,记录稀疏度。
(c) 可视化比较结果:创建三个条形图,分别比较不同变体在:
重构误差 (MSE)。
计算时间。
累积解释方差比。
(d) 将这三个比较图组合在一个大图中,保存为 10_pca_variants_comparison_metrics.png。
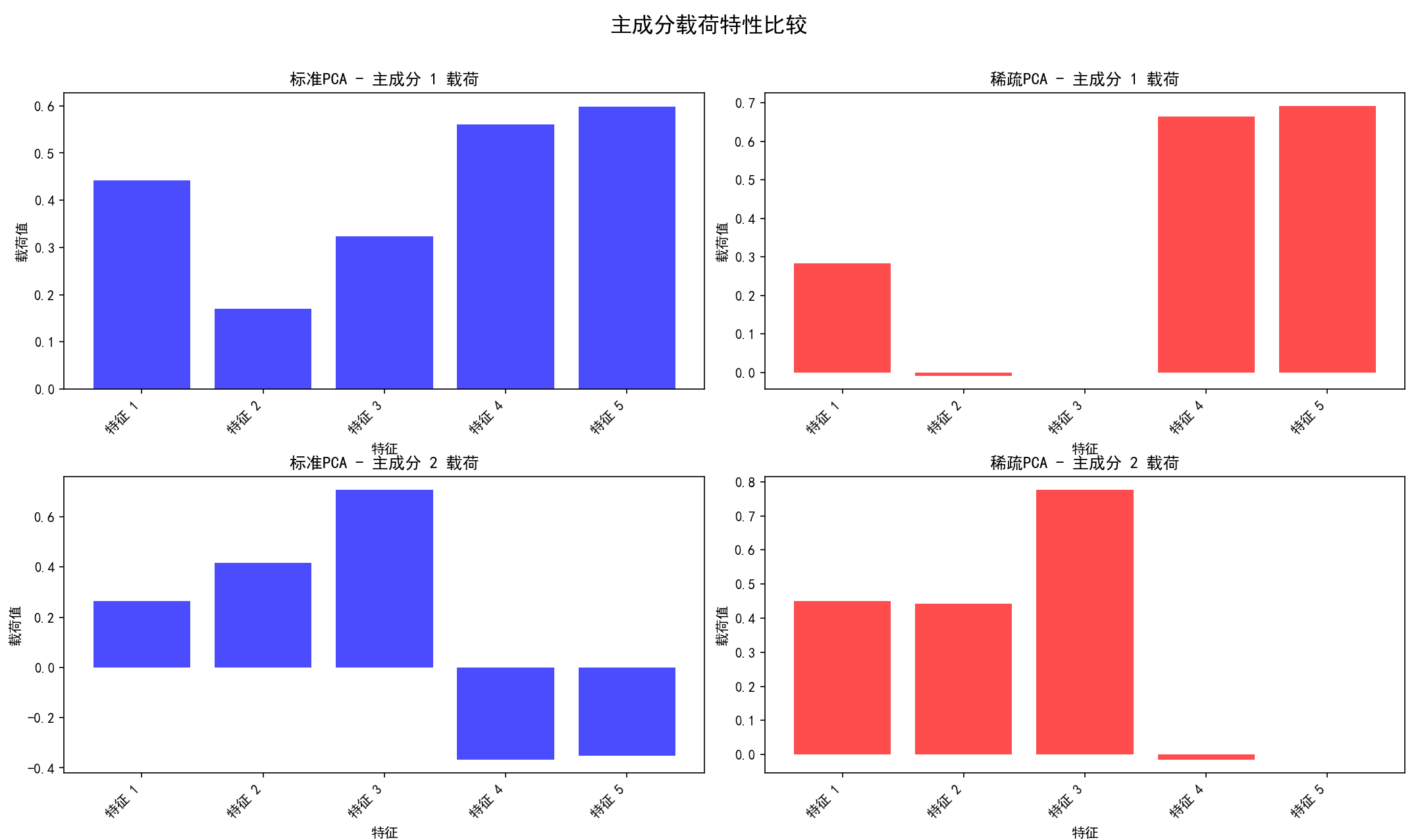
(10) 分析不同PCA变体的主成分特性 (函数 analyze_pca_components_properties 和第10部分):
a.目的:主要对比标准PCA和稀疏PCA的载荷特性。
b.步骤:
(a) 应用标准PCA和稀疏PCA。
(b) 载荷可视化:为每个选择的主成分(例如前2个),并排绘制标准PCA和稀疏PCA的载荷条形图。
保存图像为 11_pca_component_properties.png。
(c) 稀疏度分析:计算并打印两种方法载荷的非零元素比例。
(d) 解释方差比较:打印标准PCA的累积解释方差和各主成分贡献,以及稀疏PCA的近似累积解释方差。
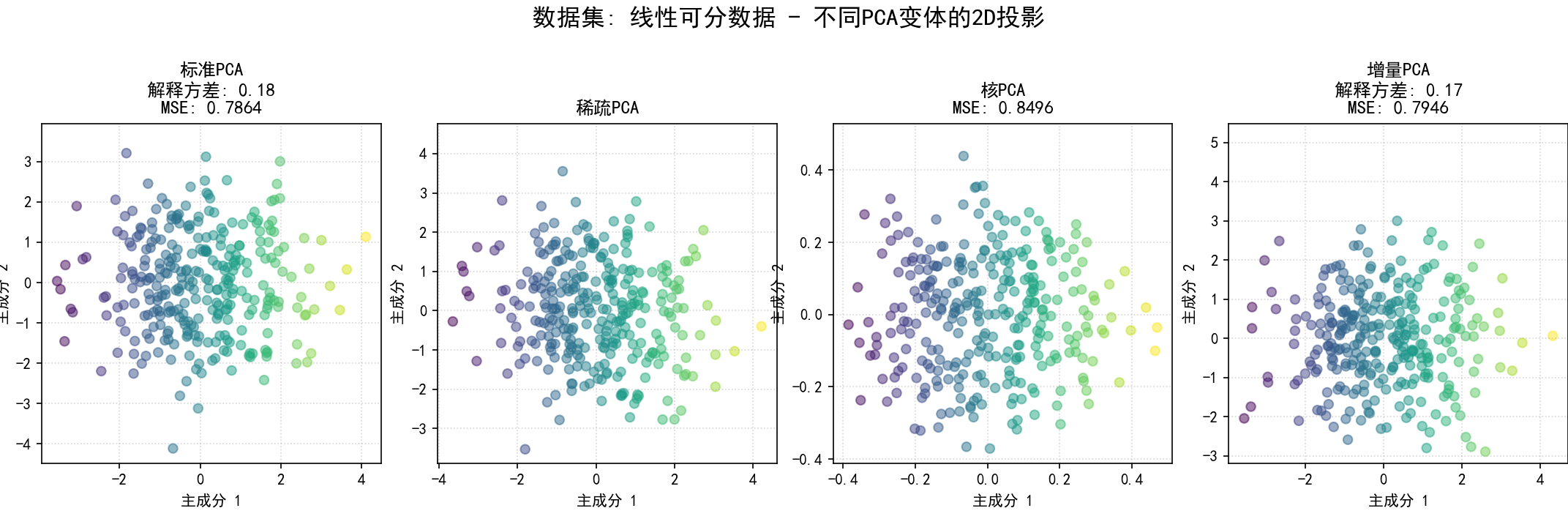
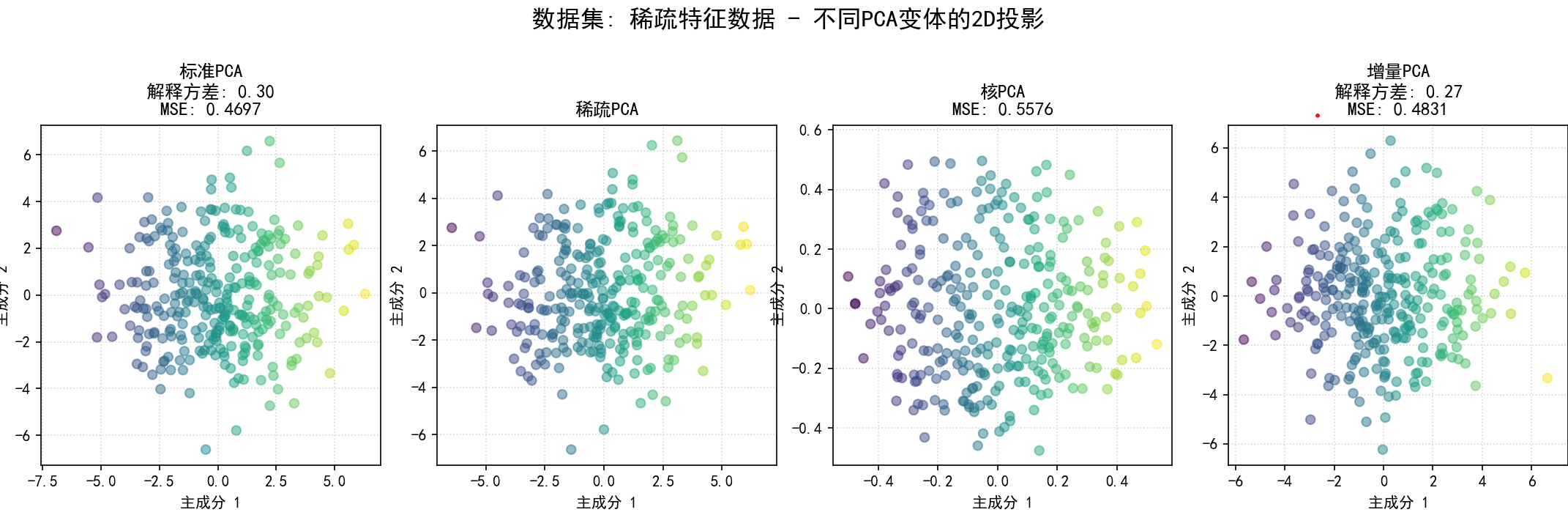
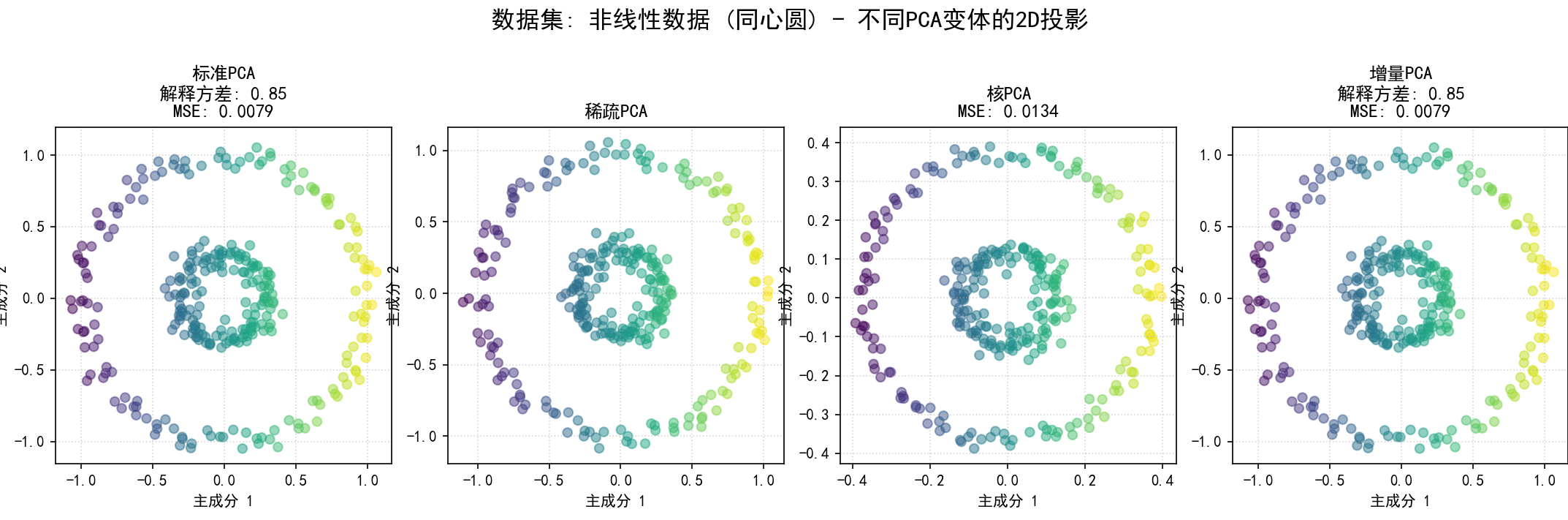
(11) 在不同类型数据集上应用PCA变体 (函数 pca_variants_on_different_datasets 和第11部分):
a.目的:展示不同PCA变体在不同数据结构(线性、稀疏特征、非线性、大规模)上的适应性和表现。
b.步骤**:
(a) 生成/定义数据集:
线性可分数据:通过混合高斯分布或引入特征间的线性相关性生成。
稀疏特征数据:大部分特征为零或噪声,少数特征包含主要信息。
非线性数据:使用 sklearn.datasets.make_circles (同心圆) 或 make_swiss_roll 生成。
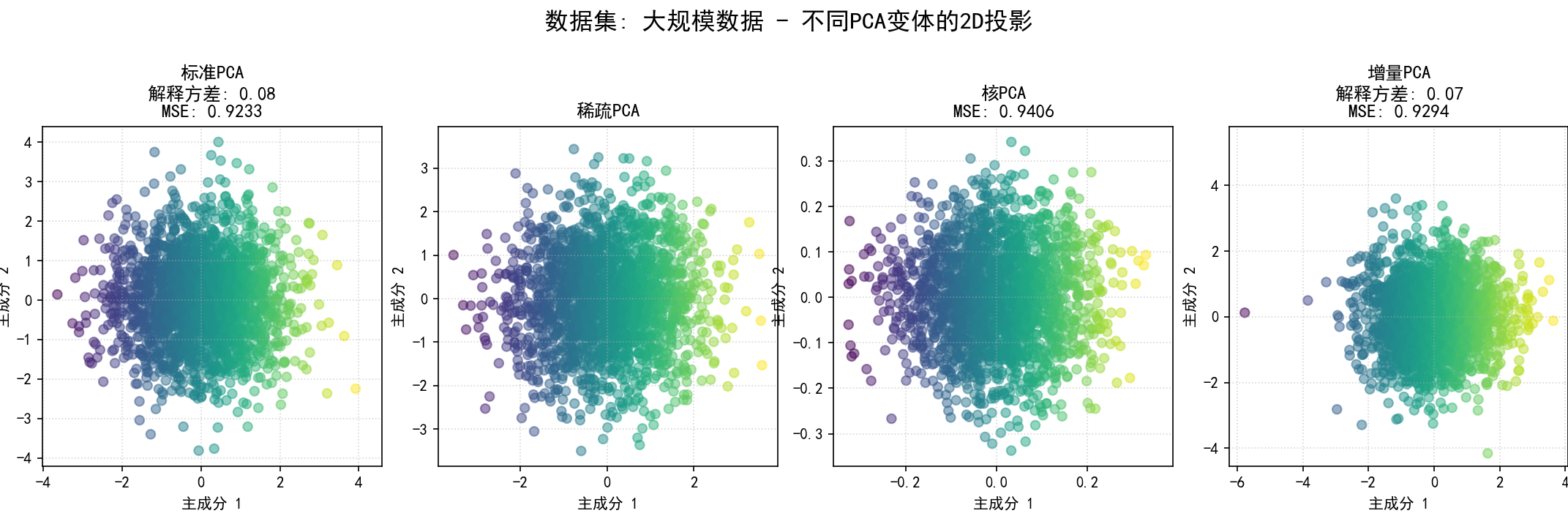
大规模数据:样本量较大的随机数据。
(b) 对于每个生成的数据集:
中心化数据。
应用标准PCA、稀疏PCA(如果数据集不大)、核PCA(如果数据集不大,通常用RBF核)和增量PCA。
记录每种方法的降维结果、解释方差(如果可用)和重构误差(如果可用)。
可视化2D投影:为当前数据集,将所有成功应用的PCA变体降维后的前两个主成分的散点图并排显示,并在标题中注明方法名称、解释方差和MSE。
为每个数据集的比较图保存为 12_pca_on_dataset_{dataset_name_sanitized}.png。
(12) 标准PCA结束语:
打印一条消息,指示标准PCA执行完毕以及图像保存的目录。
(二)主成分分析(PCA)实战的Python代码实现
先生成随机生成数据集的代码,写入CSV文件,然后Python程序访问该文件,注意随机生成数据集代码的文件(主成分分析(PCA)数据集的随机生成.py)和主成分分析(PCA)实战的文件(主成分分析(PCA)的实现.py)应位于同一目录中。

先运行"主成分分析(PCA)数据集的随机生成.py"的Python代码
import numpy as np
import pandas as pd
# 设置随机种子以保证结果可复现
np.random.seed(42)
# 定义数据集参数
n_samples = 300 # 样本数量
n_features = 5 # 原始特征数量
# 生成具有特定相关性的数据
# 我们将通过混合几个潜在的源信号来创建特征,以确保它们之间存在相关性,
# 这使得PCA降维更有意义。
# 假设有两个主要的潜在方向(源信号)
latent_source1 = np.random.randn(n_samples) * 2.5 # 第一个源信号,方差较大
latent_source2 = np.random.randn(n_samples) * 1.0 # 第二个源信号,方差较小
# 初始化数据矩阵
data = np.zeros((n_samples, n_features))
# 创建特征,使它们是潜在源信号的线性组合,并加入一些随机噪声
# 特征1: 主要由 latent_source1 驱动
data[:, 0] = 0.8 * latent_source1 + 0.2 * latent_source2 + np.random.randn(n_samples) * 0.5 + 10
# 特征2: 也主要由 latent_source1 驱动,与特征1高度相关
data[:, 1] = 0.7 * latent_source1 - 0.1 * latent_source2 + np.random.randn(n_samples) * 0.5 + 8
# 特征3: 主要由 latent_source2 驱动
data[:, 2] = 0.1 * latent_source1 + 0.9 * latent_source2 + np.random.randn(n_samples) * 0.4 + 5
# 特征4: 与 latent_source2 负相关
data[:, 3] = -0.6 * latent_source2 + np.random.randn(n_samples) * 0.6 + 12
# 特征5: 一个噪声较大或与其他特征关系较弱的特征
data[:, 4] = 0.2 * latent_source1 + 0.1 * latent_source2 + np.random.randn(n_samples) * 1.5 + 7
# 将数据转换为Pandas DataFrame,方便保存为CSV
# 使用中文列名
column_names = [f'特征_{i+1}' for i in range(n_features)]
df = pd.DataFrame(data, columns=column_names)
# 将生成的数据集保存到CSV文件
csv_file_path = 'PCA_dataset.csv'
df.to_csv(csv_file_path, index=False, encoding='utf-8-sig') # 使用utf-8-sig以确保中文正确显示
print(f"成功生成数据集 '{csv_file_path}',包含 {n_samples} 个样本和 {n_features} 个特征。")
print("\n数据集的前5行内容:")
print(df.head())
# 可以选择性地打印一些统计信息,如相关系数矩阵,以验证数据特性
print("\n特征相关系数矩阵:")
print(df.corr())
再运行"主成分分析(PCA)的实现.py"的Python代码
# 导入所有必要的库
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd # 用于数据集生成和保存
from sklearn.decomposition import PCA, SparsePCA, KernelPCA, IncrementalPCA
from sklearn.datasets import make_swiss_roll, make_circles # 用于生成非线性数据
import time # 用于测量计算时间
import os # 用于设置环境变量(备选方案)
import shutil # 用于清理临时文件夹
# 设置matplotlib支持中文显示
# 请确保您的系统中安装了SimHei字体,或者替换为您可用的中文字体
try:
plt.rcParams['font.sans-serif'] = ['SimHei'] # 指定默认字体为黑体
plt.rcParams['axes.unicode_minus'] = False # 解决保存图像是负号'-'显示为方块的问题
except Exception as e:
print(f"设置中文字体失败,可能需要手动安装或配置: {e}")
print("图形中的中文可能无法正确显示。")
# 创建一个目录来保存图像 (如果不存在)
output_image_dir = "pca_analysis_images"
if not os.path.exists(output_image_dir):
os.makedirs(output_image_dir)
print(f"图像将保存到目录: '{output_image_dir}/'")
# --- 1. 数据集生成函数 ---
def generate_pca_friendly_dataset(n_samples=300, n_features=5, n_components_strong=2,
strong_component_variance_val=20, weak_component_variance_val=2,
noise_std=0.5, file_name='pca_synthetic_data_for_report.csv'):
"""
生成一个适合PCA分析的合成数据集。
"""
print(f"开始生成数据集: {n_samples}个样本, {n_features}个特征...")
n_components_strong = min(n_components_strong, n_features)
random_matrix_for_strong = np.random.rand(n_features, n_components_strong)
q_strong, _ = np.linalg.qr(random_matrix_for_strong)
loadings_true = q_strong
scores_strong = np.random.randn(n_samples, n_components_strong) * np.sqrt(strong_component_variance_val)
data_strong_part = scores_strong @ loadings_true.T
data_weak_part = np.zeros((n_samples, n_features))
n_components_weak = n_features - n_components_strong
if n_components_weak > 0:
full_random_basis, _ = np.linalg.qr(np.random.rand(n_features, n_features))
loadings_weak = full_random_basis[:, n_components_strong:]
scores_weak = np.random.randn(n_samples, n_components_weak) * np.sqrt(weak_component_variance_val)
data_weak_part = scores_weak @ loadings_weak.T
noise = np.random.randn(n_samples, n_features) * noise_std
data = data_strong_part + data_weak_part + noise
data += np.random.rand(n_features) * 10
df = pd.DataFrame(data, columns=[f'特征_{i + 1}' for i in range(n_features)])
df.to_csv(file_name, index=False)
print(f"数据集已成功生成并保存到 '{file_name}'")
return data, loadings_true
# --- 2. 加载或生成数据 ---
DATASET_FILE = 'pca_synthetic_data_for_report.csv'
try:
data_df = pd.read_csv(DATASET_FILE)
data = data_df.values
print(f"成功从 '{DATASET_FILE}' 加载数据集,形状为: {data.shape}")
except (IOError, FileNotFoundError):
print(f"警告:找不到数据集文件 '{DATASET_FILE}' 或加载失败。将重新生成数据。")
data, _ = generate_pca_friendly_dataset(
n_samples=300, n_features=5, n_components_strong=2,
strong_component_variance_val=25, weak_component_variance_val=1,
noise_std=1.0, file_name=DATASET_FILE
)
data_centered = data - np.mean(data, axis=0)
n_samples, n_features_original = data_centered.shape
print(f"数据已中心化。样本数: {n_samples}, 特征数: {n_features_original}")
# --- 3. 标准PCA分析 ---
if n_features_original > 0:
print("\n--- 开始标准PCA分析 ---")
pca_model_full = PCA(n_components=n_features_original)
pca_model_full.fit(data_centered)
explained_variance_ratio = pca_model_full.explained_variance_ratio_
cumulative_explained_variance = np.cumsum(explained_variance_ratio)
fig_scree = plt.figure(figsize=(10, 6)) # 获取figure对象
component_indices = np.arange(1, n_features_original + 1)
plt.bar(component_indices, explained_variance_ratio, alpha=0.7, align='center', label='单个主成分解释方差比')
plt.step(component_indices, cumulative_explained_variance, where='mid', label='累积解释方差比', color='red')
plt.ylabel('解释方差比');
plt.xlabel('主成分索引');
plt.xticks(component_indices)
plt.title('碎石图 (Scree Plot)');
plt.legend(loc='best');
plt.grid(True, linestyle=':', alpha=0.7)
plt.savefig(os.path.join(output_image_dir, "01_scree_plot.png"))
plt.show()
plt.close(fig_scree) # 关闭图形
if n_features_original >= 2 and pca_model_full.components_.shape[0] >= 2:
pca_loadings = pca_model_full.components_
feature_names = [f'特征 {j + 1}' for j in range(n_features_original)]
pc1_loadings = pca_loadings[0, :];
pc2_loadings = pca_loadings[1, :]
fig_loadings, axes = plt.subplots(1, 2, figsize=(15, 5), sharey=True)
axes[0].bar(feature_names, pc1_loadings, color='skyblue');
axes[0].set_title('主成分1 (PC1) 的载荷')
axes[0].set_ylabel('载荷值');
axes[0].tick_params(axis='x', rotation=45);
axes[0].grid(True, linestyle=':', alpha=0.5, axis='y')
axes[1].bar(feature_names, pc2_loadings, color='lightcoral');
axes[1].set_title('主成分2 (PC2) 的载荷')
axes[1].tick_params(axis='x', rotation=45);
axes[1].grid(True, linestyle=':', alpha=0.5, axis='y')
plt.suptitle('主成分载荷可视化', fontsize=16);
plt.tight_layout(rect=[0, 0, 1, 0.96])
plt.savefig(os.path.join(output_image_dir, "02_pca_loadings.png"))
plt.show()
plt.close(fig_loadings)
else:
print("特征数量或计算出的主成分数量不足以展示PC1和PC2的载荷。")
else:
print("原始特征数量为0,跳过标准PCA分析。")
pca_model_full = None
# --- 4. "交互式" PCA图的静态演示 ---
if pca_model_full and n_features_original > 0:
print("\n--- PCA投影与碎石图组合演示 (静态) ---")
X_pca_full = pca_model_full.transform(data_centered)
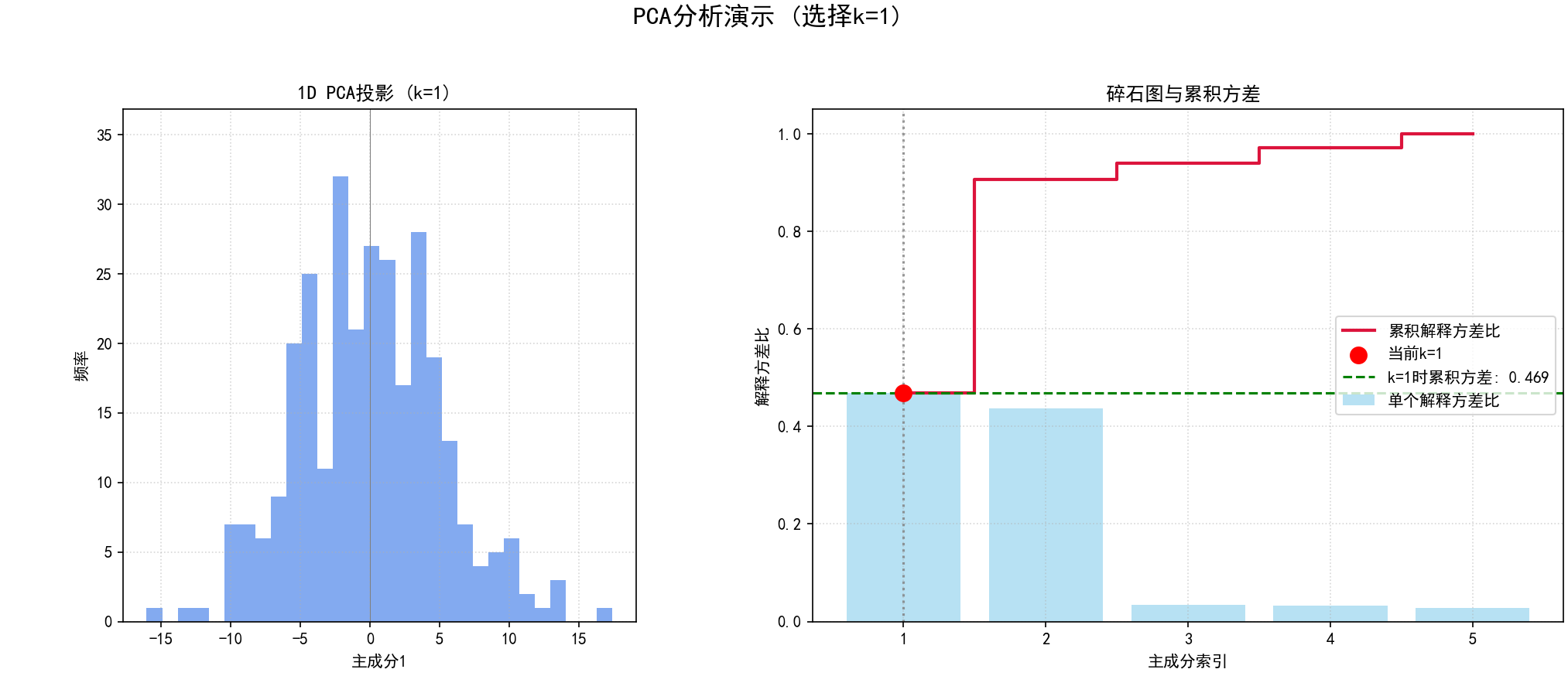
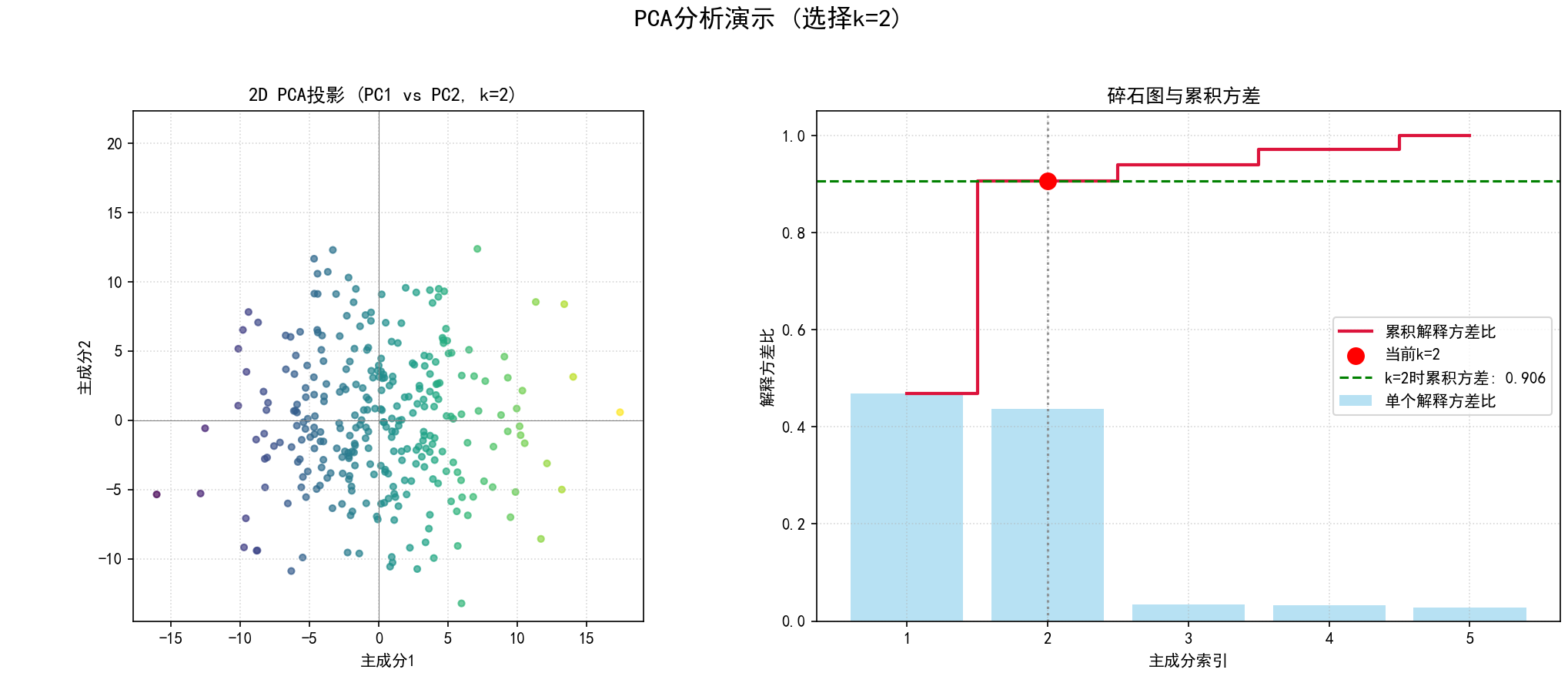
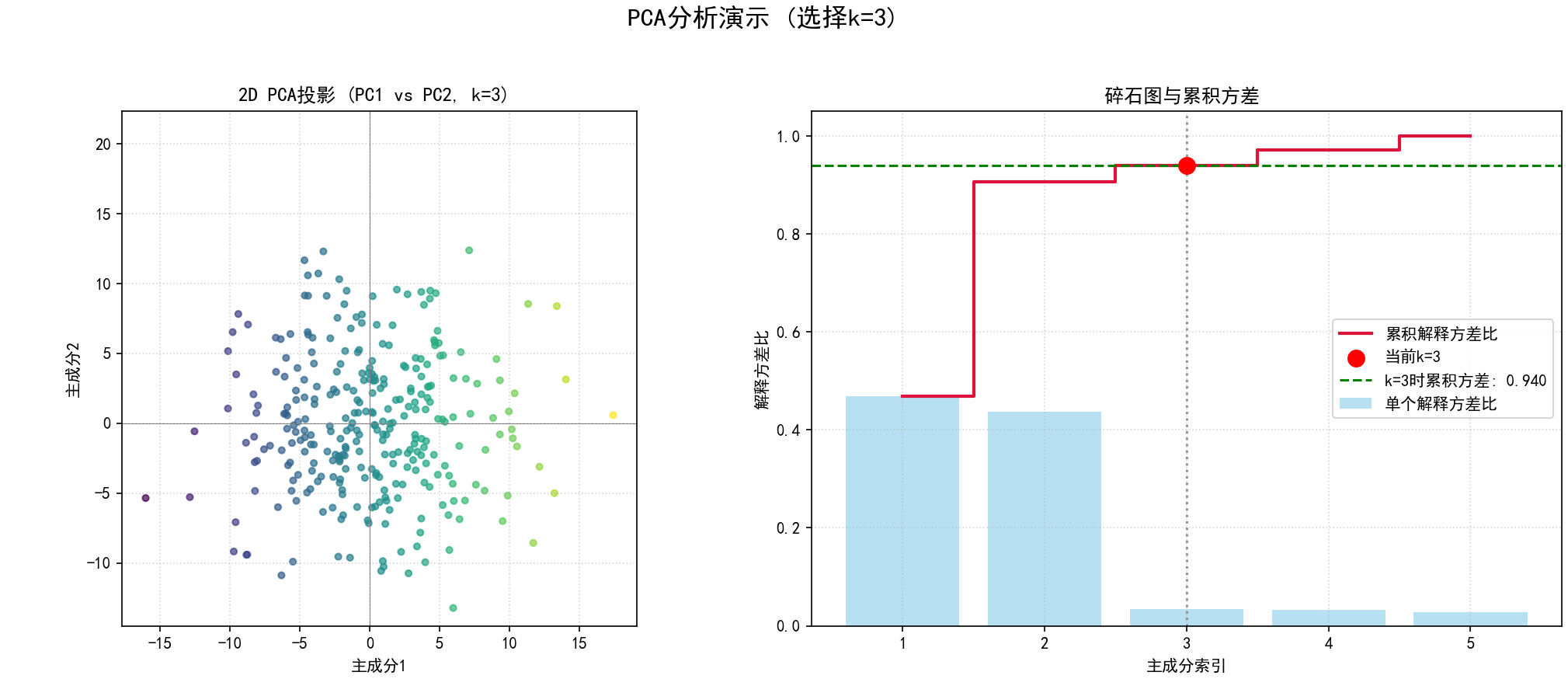
def static_pca_plot_demonstration(k_selected, X_transformed_full, evr_full, cum_evr_full, title_suffix="",
fig_idx=0):
fig_static_pca = plt.figure(figsize=(14, 6)) # 获取figure对象
plt.subplot(1, 2, 1)
if k_selected == 1 and X_transformed_full.shape[1] >= 1:
plt.hist(X_transformed_full[:, 0], bins=30, color='cornflowerblue', alpha=0.8)
plt.xlabel('主成分1');
plt.ylabel('频率');
plt.title(f'1D PCA投影 (k={k_selected}) {title_suffix}')
elif k_selected >= 2 and X_transformed_full.shape[1] >= 2:
plt.scatter(X_transformed_full[:, 0], X_transformed_full[:, 1], c=X_transformed_full[:, 0], cmap='viridis',
s=15, alpha=0.7)
plt.xlabel('主成分1');
plt.ylabel('主成分2');
plt.title(f'2D PCA投影 (PC1 vs PC2, k={k_selected}) {title_suffix}')
else:
plt.text(0.5, 0.5, '数据维度不足以绘图', horizontalalignment='center', verticalalignment='center');
plt.title(f'PCA投影 (k={k_selected}) {title_suffix}')
plt.axhline(0, color='grey', lw=0.5);
plt.axvline(0, color='grey', lw=0.5);
plt.grid(True, linestyle=':', alpha=0.5);
plt.axis('square')
plt.subplot(1, 2, 2)
num_components_total = len(evr_full);
x_axis = np.arange(1, num_components_total + 1)
plt.bar(x_axis, evr_full, alpha=0.6, align='center', label='单个解释方差比', color='skyblue')
plt.step(x_axis, cum_evr_full, where='mid', label='累积解释方差比', color='crimson', linewidth=2)
if k_selected > 0 and k_selected <= num_components_total:
plt.scatter([k_selected], [cum_evr_full[k_selected - 1]], color='red', s=100, zorder=5,
label=f'当前k={k_selected}')
plt.axhline(y=cum_evr_full[k_selected - 1], color='green', linestyle='--',
label=f'k={k_selected}时累积方差: {cum_evr_full[k_selected - 1]:.3f}')
plt.axvline(x=k_selected, color='grey', linestyle=':', alpha=0.8)
plt.ylabel('解释方差比');
plt.xlabel('主成分索引');
plt.xticks(x_axis);
plt.ylim(0, 1.05)
plt.title(f'碎石图与累积方差 {title_suffix}');
plt.legend(loc='center right');
plt.grid(True, linestyle=':', alpha=0.5)
plt.suptitle(f'PCA分析演示 (选择k={k_selected})', fontsize=16);
plt.tight_layout(rect=[0, 0, 1, 0.95])
plt.savefig(os.path.join(output_image_dir, f"03_static_pca_demo_k{k_selected}_{fig_idx}.png"))
plt.show()
plt.close(fig_static_pca)
k_demo_values = [1, 2, min(3, n_features_original)]
for idx, k_val in enumerate(k_demo_values):
if k_val > 0: static_pca_plot_demonstration(k_val, X_pca_full, explained_variance_ratio,
cumulative_explained_variance, fig_idx=idx)
# --- 5. PCA逆变换与重构误差评估 ---
if n_features_original > 0:
print("\n--- PCA逆变换与重构误差评估 ---")
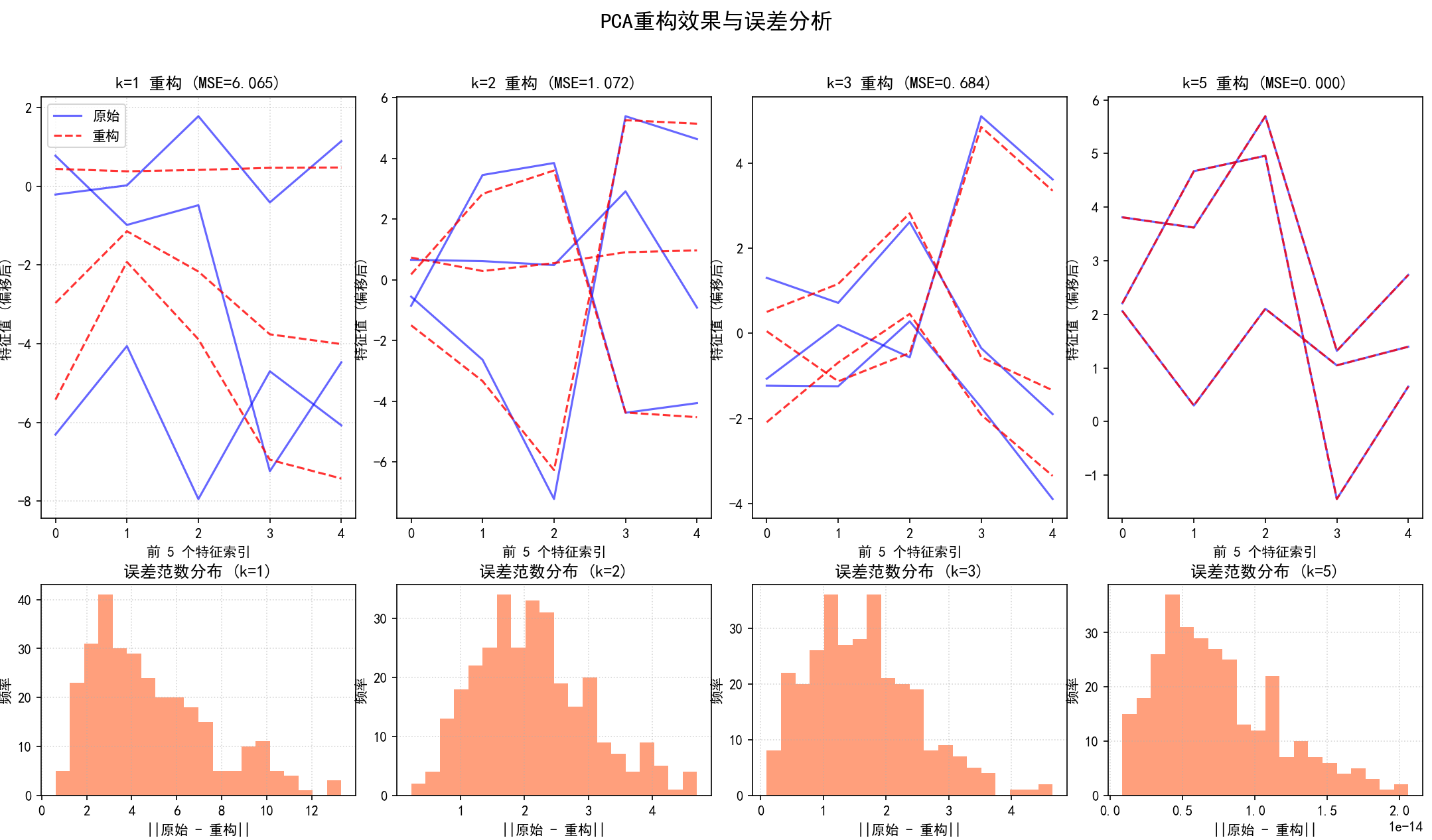
def visualize_pca_reconstruction(X_original_centered, k_values_list=None):
n_s, n_f = X_original_centered.shape
if k_values_list is None: k_values_list = [1, 2, min(3, n_f), min(5, n_f)]
k_values_list = sorted(list(set(k for k in k_values_list if 0 < k <= n_f)))
if not k_values_list: print("没有有效的k值用于重构可视化。"); return []
n_k_plots = len(k_values_list)
fig_recon, axes = plt.subplots(2, n_k_plots, figsize=(5 * n_k_plots, 10),
gridspec_kw={'height_ratios': [3, 1.5]})
if n_k_plots == 1: axes = np.array(axes).reshape(2, 1)
mse_values_list = []
for i, k_recon in enumerate(k_values_list):
pca_k_recon = PCA(n_components=k_recon);
X_reduced = pca_k_recon.fit_transform(X_original_centered)
X_reconstructed = pca_k_recon.inverse_transform(X_reduced)
mse = np.mean((X_original_centered - X_reconstructed) ** 2);
mse_values_list.append(mse)
n_samples_to_show = min(3, n_s);
n_features_to_show = min(n_f, 10)
sample_indices = np.random.choice(n_s, n_samples_to_show, replace=False)
ax_recon = axes[0, i]
for plot_idx, sample_idx in enumerate(sample_indices):
orig_sample = X_original_centered[sample_idx, :n_features_to_show];
recon_sample = X_reconstructed[sample_idx, :n_features_to_show]
offset = plot_idx * 0.2 * np.std(orig_sample) if np.std(orig_sample) > 1e-6 else plot_idx * 0.1
ax_recon.plot(np.arange(n_features_to_show), orig_sample + offset, 'b-', alpha=0.6,
label='原始' if plot_idx == 0 else "")
ax_recon.plot(np.arange(n_features_to_show), recon_sample + offset, 'r--', alpha=0.8,
label='重构' if plot_idx == 0 else "")
ax_recon.set_title(f'k={k_recon} 重构 (MSE={mse:.3f})');
ax_recon.set_xlabel(f'前 {n_features_to_show} 个特征索引');
ax_recon.set_ylabel('特征值 (偏移后)')
if i == 0: ax_recon.legend(loc='best'); ax_recon.grid(True, linestyle=':', alpha=0.5)
ax_err_dist = axes[1, i];
error_matrix = X_original_centered - X_reconstructed
error_norm_per_sample = np.linalg.norm(error_matrix, axis=1)
ax_err_dist.hist(error_norm_per_sample, bins=20, alpha=0.75, color='coral')
ax_err_dist.set_title(f'误差范数分布 (k={k_recon})');
ax_err_dist.set_xlabel('||原始 - 重构||');
ax_err_dist.set_ylabel('频率');
ax_err_dist.grid(True, linestyle=':', alpha=0.5)
fig_recon.suptitle('PCA重构效果与误差分析', fontsize=16);
plt.tight_layout(rect=[0, 0, 1, 0.95])
plt.savefig(os.path.join(output_image_dir, "04_pca_reconstruction_comparison.png"))
plt.show()
plt.close(fig_recon)
if mse_values_list:
fig_mse = plt.figure(figsize=(8, 5));
plt.plot(k_values_list, mse_values_list, 'bo-', linewidth=2, markersize=8)
plt.xlabel('主成分数量 (k)');
plt.ylabel('平均重构误差 (MSE)');
plt.title('PCA重构误差与主成分数量的关系')
plt.xticks(k_values_list);
plt.grid(True, linestyle=':', alpha=0.7)
plt.savefig(os.path.join(output_image_dir, "05_pca_reconstruction_mse_vs_k.png"))
plt.show()
plt.close(fig_mse)
return mse_values_list
mse_standard_pca = visualize_pca_reconstruction(data_centered)
# --- 6. 稀疏PCA (Sparse PCA) ---
if n_features_original > 0:
print("\n--- 稀疏PCA (Sparse PCA) ---")
def implement_sparse_pca(X_cent, n_comp=2, alpha_val=1.0):
if n_comp == 0: print("稀疏PCA的n_components为0,跳过。"); return None, None
pca_std_ref = PCA(n_components=n_comp);
X_pca_std_ref = pca_std_ref.fit_transform(X_cent)
sparse_pca_model = SparsePCA(n_components=n_comp, alpha=alpha_val, random_state=42, n_jobs=1)
X_sparse_pca_proj = sparse_pca_model.fit_transform(X_cent)
fig_spca_loadings, axes_sp = plt.subplots(1, 2, figsize=(14, 6))
std_loadings_ref = pca_std_ref.components_
vmin_val_std = -np.max(np.abs(std_loadings_ref)) if std_loadings_ref.size > 0 else 0
vmax_val_std = np.max(np.abs(std_loadings_ref)) if std_loadings_ref.size > 0 else 0
im_std = axes_sp[0].imshow(std_loadings_ref, cmap='coolwarm', aspect='auto', vmin=vmin_val_std,
vmax=vmax_val_std)
axes_sp[0].set_title('标准PCA载荷');
axes_sp[0].set_xlabel('原始特征索引');
axes_sp[0].set_ylabel('主成分索引');
fig_spca_loadings.colorbar(im_std, ax=axes_sp[0], label='载荷值')
sparse_loadings_val = sparse_pca_model.components_
vmin_val_sparse = -np.max(np.abs(sparse_loadings_val)) if sparse_loadings_val.size > 0 else 0
vmax_val_sparse = np.max(np.abs(sparse_loadings_val)) if sparse_loadings_val.size > 0 else 0
im_sparse = axes_sp[1].imshow(sparse_loadings_val, cmap='coolwarm', aspect='auto', vmin=vmin_val_sparse,
vmax=vmax_val_sparse)
axes_sp[1].set_title(f'稀疏PCA载荷 (alpha={alpha_val})');
axes_sp[1].set_xlabel('原始特征索引');
axes_sp[1].set_ylabel('主成分索引');
fig_spca_loadings.colorbar(im_sparse, ax=axes_sp[1], label='载荷值')
fig_spca_loadings.suptitle('标准PCA与稀疏PCA载荷比较', fontsize=16);
plt.tight_layout(rect=[0, 0, 1, 0.95])
plt.savefig(os.path.join(output_image_dir, f"06_sparse_pca_loadings_alpha{alpha_val}.png"))
plt.show()
plt.close(fig_spca_loadings)
if n_comp >= 2 and X_pca_std_ref.shape[1] >= 2 and X_sparse_pca_proj.shape[1] >= 2:
fig_spca_proj = plt.figure(figsize=(12, 5));
plt.subplot(1, 2, 1)
plt.scatter(X_pca_std_ref[:, 0], X_pca_std_ref[:, 1], c=X_pca_std_ref[:, 0], cmap='winter', alpha=0.6)
plt.title('标准PCA投影 (PC1 vs PC2)');
plt.xlabel('主成分 1');
plt.ylabel('主成分 2');
plt.grid(True, linestyle=':', alpha=0.5);
plt.axis('square')
plt.subplot(1, 2, 2)
plt.scatter(X_sparse_pca_proj[:, 0], X_sparse_pca_proj[:, 1], c=X_sparse_pca_proj[:, 0], cmap='autumn',
alpha=0.6)
plt.title(f'稀疏PCA投影 (alpha={alpha_val})');
plt.xlabel('主成分 1');
plt.ylabel('主成分 2');
plt.grid(True, linestyle=':', alpha=0.5);
plt.axis('square')
plt.suptitle('降维结果比较 (标准PCA vs 稀疏PCA)', fontsize=16);
plt.tight_layout(rect=[0, 0, 1, 0.95])
plt.savefig(os.path.join(output_image_dir, f"07_sparse_pca_projection_alpha{alpha_val}.png"))
plt.show()
plt.close(fig_spca_proj)
std_non_zero = np.count_nonzero(
np.abs(std_loadings_ref) > 1e-6) / std_loadings_ref.size if std_loadings_ref.size > 0 else 0
sparse_non_zero = np.count_nonzero(
np.abs(sparse_loadings_val) > 1e-6) / sparse_loadings_val.size if sparse_loadings_val.size > 0 else 0
print(f"标准PCA载荷的非零元素近似比例: {std_non_zero:.2%}")
print(f"稀疏PCA (alpha={alpha_val}) 载荷的非零元素近似比例: {sparse_non_zero:.2%}")
return pca_std_ref, sparse_pca_model
if n_features_original >= 1: implement_sparse_pca(data_centered, n_comp=min(2, n_features_original), alpha_val=1.0)
# --- 7. 核PCA (Kernel PCA) ---
if n_features_original > 0:
print("\n--- 核PCA (Kernel PCA) ---")
def implement_kernel_pca(X_cent, n_comp=2):
if n_comp == 0: print("核PCA的n_components为0,跳过。"); return None, {}
if n_comp > X_cent.shape[1]: n_comp = X_cent.shape[1]
pca_std_ref = PCA(n_components=n_comp);
X_pca_std_ref = pca_std_ref.fit_transform(X_cent)
kernels_to_test = ['linear', 'poly', 'rbf', 'sigmoid'];
kernel_pcas_dict = {};
X_kpcas_dict = {}
gamma_val = 1.0 / X_cent.shape[1] if X_cent.shape[1] > 0 else None
for kernel_name in kernels_to_test:
try:
kpca_model = KernelPCA(n_components=n_comp, kernel=kernel_name, gamma=gamma_val,
fit_inverse_transform=True, random_state=42)
X_kpca_proj = kpca_model.fit_transform(X_cent);
kernel_pcas_dict[kernel_name] = kpca_model;
X_kpcas_dict[kernel_name] = X_kpca_proj
except Exception as e:
print(f"执行核PCA ({kernel_name}) 失败: {e}"); kernel_pcas_dict[kernel_name] = None; X_kpcas_dict[
kernel_name] = None
valid_kpcas = {k: v for k, v in X_kpcas_dict.items() if v is not None and v.shape[1] >= 2}
num_plots = (1 if X_pca_std_ref is not None and X_pca_std_ref.shape[1] >= 2 else 0) + len(valid_kpcas)
if num_plots == 0: print("没有成功的(核)PCA二维投影可供可视化。"); return pca_std_ref, kernel_pcas_dict
cols = 3;
rows = (num_plots + cols - 1) // cols
fig_kpca = plt.figure(figsize=(5 * cols, 5 * rows)) # 获取figure对象
plot_idx = 1
if X_pca_std_ref is not None and X_pca_std_ref.shape[1] >= 2:
plt.subplot(rows, cols, plot_idx);
plot_idx += 1
plt.scatter(X_pca_std_ref[:, 0], X_pca_std_ref[:, 1], c=X_pca_std_ref[:, 0], cmap='winter', alpha=0.6)
plt.title('标准PCA');
plt.xlabel('PC1');
plt.ylabel('PC2');
plt.grid(True, linestyle=':', alpha=0.5);
plt.axis('square')
for kernel_name, X_kpca_proj_val in valid_kpcas.items():
plt.subplot(rows, cols, plot_idx);
plot_idx += 1
plt.scatter(X_kpca_proj_val[:, 0], X_kpca_proj_val[:, 1], c=X_kpca_proj_val[:, 0], cmap='cool', alpha=0.6)
plt.title(f'核PCA ({kernel_name})');
plt.xlabel('PC1');
plt.ylabel('PC2');
plt.grid(True, linestyle=':', alpha=0.5);
plt.axis('square')
plt.suptitle('核PCA降维结果比较', fontsize=16);
plt.tight_layout(rect=[0, 0, 1, 0.95])
plt.savefig(os.path.join(output_image_dir, "08_kernel_pca_projections.png"))
plt.show()
plt.close(fig_kpca)
print("\n核PCA重构误差 (MSE):")
if X_pca_std_ref is not None:
X_back_std_ref = pca_std_ref.inverse_transform(X_pca_std_ref)
error_std_ref = np.mean((X_cent - X_back_std_ref) ** 2);
print(f" 标准PCA (参考): {error_std_ref:.4f}")
for kernel_name, kpca_model_val in kernel_pcas_dict.items():
if kpca_model_val is not None and X_kpcas_dict[kernel_name] is not None:
try:
X_back_kpca = kpca_model_val.inverse_transform(X_kpcas_dict[kernel_name])
error_kpca = np.mean((X_cent - X_back_kpca) ** 2);
print(f" {kernel_name} 核: {error_kpca:.4f}")
except Exception as e:
print(f" {kernel_name} 核: 无法计算重构误差 ({e})")
return pca_std_ref, kernel_pcas_dict
if n_features_original >= 1: implement_kernel_pca(data_centered, n_comp=min(2, n_features_original))
# --- 8. 增量PCA (Incremental PCA) ---
if n_features_original > 0:
print("\n--- 增量PCA (Incremental PCA) ---")
def implement_incremental_pca(X_cent, n_comp=2, batch_s=None):
if n_comp == 0: print("增量PCA的n_components为0,跳过。"); return None, None, np.nan, np.nan
if n_comp > X_cent.shape[1]: n_comp = X_cent.shape[1]
n_s_ipca = X_cent.shape[0]
if batch_s is None: batch_s = max(n_comp * 2 if n_comp > 0 else 1, n_s_ipca // 10 if n_s_ipca // 10 > 0 else 1)
start_std = time.time();
pca_std_ref = PCA(n_components=n_comp);
X_pca_std_proj = pca_std_ref.fit_transform(X_cent);
time_std = time.time() - start_std
start_ipca = time.time();
ipca_model = IncrementalPCA(n_components=n_comp, batch_size=batch_s);
X_ipca_proj = ipca_model.fit_transform(X_cent);
time_ipca = time.time() - start_ipca
if n_comp >= 2 and X_pca_std_proj.shape[1] >= 2 and X_ipca_proj.shape[1] >= 2:
fig_ipca = plt.figure(figsize=(12, 5));
plt.subplot(1, 2, 1) # 获取figure对象
plt.scatter(X_pca_std_proj[:, 0], X_pca_std_proj[:, 1], c=X_pca_std_proj[:, 0], cmap='winter', alpha=0.6)
plt.title(f'标准PCA (用时: {time_std:.3f}s)');
plt.xlabel('PC1');
plt.ylabel('PC2');
plt.grid(True, linestyle=':', alpha=0.5);
plt.axis('square')
plt.subplot(1, 2, 2)
plt.scatter(X_ipca_proj[:, 0], X_ipca_proj[:, 1], c=X_ipca_proj[:, 0], cmap='summer', alpha=0.6)
plt.title(f'增量PCA (用时: {time_ipca:.3f}s, 批大小: {batch_s})');
plt.xlabel('PC1');
plt.ylabel('PC2');
plt.grid(True, linestyle=':', alpha=0.5);
plt.axis('square')
plt.suptitle('标准PCA与增量PCA降维结果比较', fontsize=16);
plt.tight_layout(rect=[0, 0, 1, 0.95])
plt.savefig(os.path.join(output_image_dir, "09_incremental_pca_comparison.png"))
plt.show()
plt.close(fig_ipca)
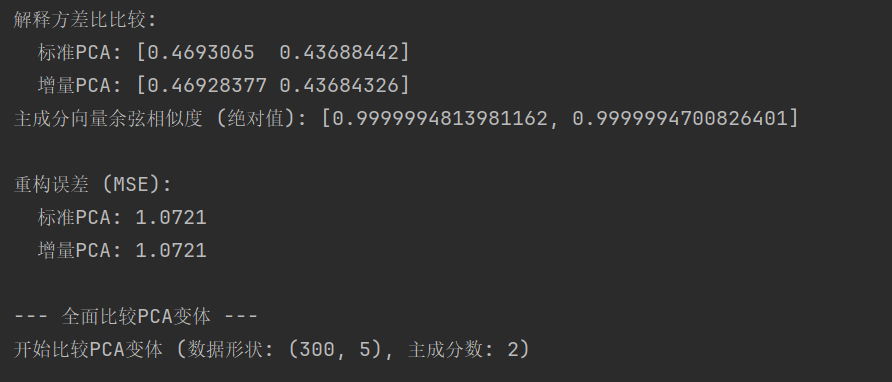
print("\n解释方差比比较:");
print(f" 标准PCA: {pca_std_ref.explained_variance_ratio_}");
print(f" 增量PCA: {ipca_model.explained_variance_ratio_}")
min_comps = min(len(pca_std_ref.components_), len(ipca_model.components_))
if min_comps > 0:
similarity_scores = [np.abs(np.dot(pca_std_ref.components_[i], ipca_model.components_[i])) for i in
range(min_comps)]
print(f"主成分向量余弦相似度 (绝对值): {similarity_scores}")
X_back_std_ipca = pca_std_ref.inverse_transform(X_pca_std_proj);
X_back_ipca = ipca_model.inverse_transform(X_ipca_proj)
error_std_ipca = np.mean((X_cent - X_back_std_ipca) ** 2);
error_ipca_val = np.mean((X_cent - X_back_ipca) ** 2)
print("\n重构误差 (MSE):");
print(f" 标准PCA: {error_std_ipca:.4f}");
print(f" 增量PCA: {error_ipca_val:.4f}")
return pca_std_ref, ipca_model, error_std_ipca, error_ipca_val
if n_features_original >= 1: implement_incremental_pca(data_centered, n_comp=min(2, n_features_original))
# --- 9. 全面比较PCA变体 ---
if n_features_original > 0:
print("\n--- 全面比较PCA变体 ---")
def compare_all_pca_variants(X_cent, n_comp=2):
n_s_comp, n_f_comp = X_cent.shape
if n_comp == 0: print("比较PCA变体时n_components为0,跳过。"); return {}
if n_comp > n_f_comp: n_comp = n_f_comp
results_dict = {};
print(f"开始比较PCA变体 (数据形状: {X_cent.shape}, 主成分数: {n_comp})")
start_t = time.time();
pca_std_comp = PCA(n_components=n_comp);
X_pca_std_comp = pca_std_comp.fit_transform(X_cent)
X_back_std_comp = pca_std_comp.inverse_transform(X_pca_std_comp);
err_std = np.mean((X_cent - X_back_std_comp) ** 2)
time_std_comp = time.time() - start_t
results_dict['标准PCA'] = {'explained_variance_ratio': pca_std_comp.explained_variance_ratio_,
'cumulative_variance': np.sum(pca_std_comp.explained_variance_ratio_),
'reconstruction_error': err_std, 'computation_time': time_std_comp}
alpha_sparse_comp = 1.0;
start_t = time.time()
spca_comp = SparsePCA(n_components=n_comp, alpha=alpha_sparse_comp, random_state=42, n_jobs=1);
_ = spca_comp.fit_transform(X_cent)
sparsity_val = 1.0 - (np.count_nonzero(
spca_comp.components_ == 0) / spca_comp.components_.size if spca_comp.components_.size > 0 else 0);
time_spca_comp = time.time() - start_t
results_dict[f'稀疏PCA (α={alpha_sparse_comp})'] = {'sparsity': sparsity_val,
'computation_time': time_spca_comp,
'reconstruction_error': np.nan,
'cumulative_variance': np.nan}
if n_s_comp * n_f_comp < 500000:
kernel_name_comp = 'rbf';
gamma_comp = 1.0 / n_f_comp if n_f_comp > 0 else None;
start_t = time.time()
kpca_comp = KernelPCA(n_components=n_comp, kernel=kernel_name_comp, gamma=gamma_comp,
fit_inverse_transform=True, random_state=42)
X_kpca_comp_proj = kpca_comp.fit_transform(X_cent);
time_kpca_comp = time.time() - start_t
cum_var_kpca = np.sum(kpca_comp.lambdas_[:n_comp]) / np.sum(kpca_comp.lambdas_) if hasattr(kpca_comp,
'lambdas_') and kpca_comp.lambdas_ is not None and np.sum(
kpca_comp.lambdas_) > 1e-9 else np.nan
err_kpca = np.nan;
try:
X_back_kpca_comp = kpca_comp.inverse_transform(X_kpca_comp_proj); err_kpca = np.mean(
(X_cent - X_back_kpca_comp) ** 2)
except:
pass
results_dict[f'核PCA ({kernel_name_comp})'] = {'cumulative_variance': cum_var_kpca,
'reconstruction_error': err_kpca,
'computation_time': time_kpca_comp}
else:
print("数据集较大,跳过核PCA的全面比较部分以节省时间。")
batch_s_comp = max(n_comp * 2 if n_comp > 0 else 1, n_s_comp // 10 if n_s_comp // 10 > 0 else 1);
start_t = time.time()
ipca_comp = IncrementalPCA(n_components=n_comp, batch_size=batch_s_comp);
X_ipca_comp_proj = ipca_comp.fit_transform(X_cent)
X_back_ipca_comp = ipca_comp.inverse_transform(X_ipca_comp_proj);
err_ipca = np.mean((X_cent - X_back_ipca_comp) ** 2)
time_ipca_comp = time.time() - start_t
results_dict[f'增量PCA (批={batch_s_comp})'] = {'explained_variance_ratio': ipca_comp.explained_variance_ratio_,
'cumulative_variance': np.sum(
ipca_comp.explained_variance_ratio_),
'reconstruction_error': err_ipca,
'computation_time': time_ipca_comp}
methods_list = [];
errors_list = [];
times_list = [];
cum_vars_list = []
for method, res in results_dict.items():
methods_list.append(method);
errors_list.append(res.get('reconstruction_error', np.nan))
times_list.append(res.get('computation_time', np.nan));
cum_vars_list.append(res.get('cumulative_variance', np.nan))
valid_indices_error = [i for i, x in enumerate(errors_list) if not np.isnan(x)];
valid_indices_time = [i for i, x in enumerate(times_list) if not np.isnan(x)];
valid_indices_cumvar = [i for i, x in enumerate(cum_vars_list) if not np.isnan(x)]
fig_comp_metrics, axes_comp = plt.subplots(3, 1, figsize=(12, 18)) # 获取figure对象
ax = axes_comp[0];
m_err = [methods_list[i] for i in valid_indices_error];
e_err = [errors_list[i] for i in valid_indices_error]
if m_err: bars_err = ax.bar(m_err, e_err, color=plt.cm.viridis(np.linspace(0, 1, len(m_err)))); [
ax.text(bar.get_x() + bar.get_width() / 2., bar.get_height(), f'{bar.get_height():.4f}', ha='center',
va='bottom') for bar in bars_err]
ax.set_ylabel('重构误差 (MSE)');
ax.set_title(f'不同PCA变体的重构误差 (k={n_comp})');
ax.tick_params(axis='x', rotation=30)
ax = axes_comp[1];
m_time = [methods_list[i] for i in valid_indices_time];
t_time = [times_list[i] for i in valid_indices_time]
if m_time: bars_time = ax.bar(m_time, t_time, color=plt.cm.plasma(np.linspace(0, 1, len(m_time)))); [
ax.text(bar.get_x() + bar.get_width() / 2., bar.get_height(), f'{bar.get_height():.3f}s', ha='center',
va='bottom') for bar in bars_time]
ax.set_ylabel('计算时间 (秒)');
ax.set_title(f'不同PCA变体的计算时间 (k={n_comp})');
ax.tick_params(axis='x', rotation=30)
ax = axes_comp[2];
m_cv = [methods_list[i] for i in valid_indices_cumvar];
cv_cv = [cum_vars_list[i] for i in valid_indices_cumvar]
if m_cv: bars_cv = ax.bar(m_cv, cv_cv, color=plt.cm.cividis(np.linspace(0, 1, len(m_cv)))); [
ax.text(bar.get_x() + bar.get_width() / 2., bar.get_height(), f'{bar.get_height():.3f}', ha='center',
va='bottom') for bar in bars_cv]
ax.set_ylabel(f'累积解释方差比 (前{n_comp}个主成分)');
ax.set_title(f'不同PCA变体的累积解释方差比 (k={n_comp})');
ax.tick_params(axis='x', rotation=30);
ax.set_ylim(0, 1.1)
fig_comp_metrics.suptitle('PCA变体性能综合比较', fontsize=18);
plt.tight_layout(rect=[0, 0, 1, 0.96])
plt.savefig(os.path.join(output_image_dir, "10_pca_variants_comparison_metrics.png"))
plt.show()
plt.close(fig_comp_metrics)
return results_dict
if n_features_original >= 1: compare_all_pca_variants(data_centered, n_comp=min(2, n_features_original))
# --- 10. 分析不同PCA变体的主成分特性 ---
if n_features_original > 0:
print("\n--- 分析不同PCA变体的主成分特性 ---")
def analyze_pca_components_properties(X, n_comp=2):
if n_comp == 0: print("主成分特性分析的n_components为0,跳过。"); return None, None
if n_comp > X.shape[1]: n_comp = X.shape[1]
pca_std = PCA(n_components=n_comp);
pca_std.fit(X)
sparse_pca = SparsePCA(n_components=n_comp, alpha=1.0, random_state=42, n_jobs=1);
sparse_pca.fit(X)
n_f_prop = X.shape[1];
feature_names_prop = [f'特征 {i + 1}' for i in range(n_f_prop)]
actual_n_comp = min(n_comp, pca_std.components_.shape[0] if pca_std.components_ is not None else 0,
sparse_pca.components_.shape[0] if sparse_pca.components_ is not None else 0)
if actual_n_comp == 0: print("没有足够的主成分用于载荷可视化。"); return pca_std, sparse_pca
fig_comp_props = plt.figure(figsize=(15, 5 * actual_n_comp)) # 获取figure对象
for i in range(actual_n_comp):
plt.subplot(actual_n_comp, 2, 2 * i + 1)
plt.bar(feature_names_prop, pca_std.components_[i], color='blue', alpha=0.7)
plt.title(f'标准PCA - 主成分 {i + 1} 载荷');
plt.xlabel('特征');
plt.ylabel('载荷值');
plt.xticks(rotation=45, ha='right')
plt.subplot(actual_n_comp, 2, 2 * i + 2)
plt.bar(feature_names_prop, sparse_pca.components_[i], color='red', alpha=0.7)
plt.title(f'稀疏PCA - 主成分 {i + 1} 载荷');
plt.xlabel('特征');
plt.ylabel('载荷值');
plt.xticks(rotation=45, ha='right')
plt.suptitle('主成分载荷特性比较', fontsize=16);
plt.tight_layout(rect=[0, 0, 1, 0.96])
plt.savefig(os.path.join(output_image_dir, "11_pca_component_properties.png"))
plt.show()
plt.close(fig_comp_props)
std_nonzeros = np.count_nonzero(
np.abs(pca_std.components_) > 1e-10) / pca_std.components_.size if pca_std.components_.size > 0 else 0
sparse_nonzeros = np.count_nonzero(np.abs(
sparse_pca.components_) > 1e-10) / sparse_pca.components_.size if sparse_pca.components_.size > 0 else 0
print(f"标准PCA载荷的非零元素比例: {std_nonzeros:.2%}");
print(f"稀疏PCA载荷的非零元素比例: {sparse_nonzeros:.2%}")
total_var_std = np.sum(pca_std.explained_variance_ratio_);
print(f"\n标准PCA的累积解释方差比 (k={actual_n_comp}): {total_var_std:.4f}");
print(f"各主成分的贡献: {pca_std.explained_variance_ratio_}")
X_trans = sparse_pca.transform(X);
X_approx = X_trans @ sparse_pca.components_
var_tot = np.var(X, axis=0).sum();
var_res = np.var(X - X_approx, axis=0).sum()
sparse_expl_var = (1 - var_res / var_tot) if var_tot > 1e-9 else 0.0
print(f"\n稀疏PCA的近似累积解释方差比: {sparse_expl_var:.4f}")
return pca_std, sparse_pca
if n_features_original >= 1: analyze_pca_components_properties(data_centered, n_comp=min(2, n_features_original))
# --- 11. 在不同类型数据集上应用PCA变体 ---
print("\n--- 在不同类型数据集上应用PCA变体 ---")
def pca_variants_on_different_datasets():
datasets = {};
np.random.seed(42);
n_s_diff = 300
X_linear = np.random.randn(n_s_diff, 20);
X_linear[:, 0] = X_linear[:, 1] * 0.8 + X_linear[:, 0] * 0.2;
X_linear[:, 2] = X_linear[:, 3] * 0.7 + X_linear[:, 2] * 0.3;
datasets['线性可分数据'] = X_linear
X_sparse_features = np.zeros((n_s_diff, 50));
X_sparse_features[:, 0:5] = np.random.randn(n_s_diff, 5) * 2;
X_sparse_features[:, 20:25] = np.random.randn(n_s_diff, 5) * 1.5;
X_sparse_features += np.random.randn(*X_sparse_features.shape) * 0.1;
datasets['稀疏特征数据'] = X_sparse_features
X_nonlinear, _ = make_circles(n_samples=n_s_diff, factor=0.3, noise=0.05, random_state=42);
noise_dims = np.random.randn(n_s_diff, 10) * 0.1;
X_nonlinear = np.hstack([X_nonlinear, noise_dims]);
datasets['非线性数据 (同心圆)'] = X_nonlinear
X_large = np.random.randn(2000, 30);
[(X_large[:, i] + X_large[:, j] * 0.1) for i in range(5) for j in range(i + 1, 5)];
datasets['大规模数据'] = X_large
n_comp_diff = 2;
results_diff = {}
for dataset_name, X_d in datasets.items():
print(f"\n处理数据集: {dataset_name} (形状: {X_d.shape})");
X_centered_d = X_d - np.mean(X_d, axis=0)
if X_centered_d.shape[1] == 0: print(f"数据集 {dataset_name} 特征数为0,跳过。"); continue
actual_n_comp_diff = min(n_comp_diff, X_centered_d.shape[1])
if actual_n_comp_diff == 0: print(f"数据集 {dataset_name} 计算出的主成分数为0,跳过。"); continue
dataset_results = {}
pca_std_d = PCA(n_components=actual_n_comp_diff);
X_pca_std_d = pca_std_d.fit_transform(X_centered_d);
X_back_std_d = pca_std_d.inverse_transform(X_pca_std_d);
error_std_d = np.mean((X_centered_d - X_back_std_d) ** 2)
dataset_results['标准PCA'] = {'transformed_data': X_pca_std_d,
'explained_variance_ratio': pca_std_d.explained_variance_ratio_,
'cumulative_variance': np.sum(pca_std_d.explained_variance_ratio_),
'reconstruction_error': error_std_d}
if X_d.shape[0] * X_d.shape[1] < 500000 and X_d.shape[1] > 0:
sparse_pca_d = SparsePCA(n_components=actual_n_comp_diff, alpha=0.1, random_state=42, n_jobs=1);
X_sparse_d = sparse_pca_d.fit_transform(X_centered_d)
dataset_results['稀疏PCA'] = {'transformed_data': X_sparse_d}
gamma_d = 1.0 / X_d.shape[1] if X_d.shape[1] > 0 else None
kernel_pca_d = KernelPCA(n_components=actual_n_comp_diff, kernel='rbf', gamma=gamma_d,
fit_inverse_transform=True, random_state=42);
X_kernel_d = kernel_pca_d.fit_transform(X_centered_d)
error_kernel_d = None;
try:
X_back_kernel_d = kernel_pca_d.inverse_transform(X_kernel_d); error_kernel_d = np.mean(
(X_centered_d - X_back_kernel_d) ** 2)
except:
pass
dataset_results['核PCA'] = {'transformed_data': X_kernel_d, 'reconstruction_error': error_kernel_d}
batch_size_d = max(actual_n_comp_diff * 2 if actual_n_comp_diff > 0 else 1,
X_d.shape[0] // 10 if X_d.shape[0] // 10 > 0 else 1)
ipca_d = IncrementalPCA(n_components=actual_n_comp_diff, batch_size=batch_size_d);
X_ipca_d = ipca_d.fit_transform(X_centered_d);
X_back_ipca_d = ipca_d.inverse_transform(X_ipca_d);
error_ipca_d = np.mean((X_centered_d - X_back_ipca_d) ** 2)
dataset_results['增量PCA'] = {'transformed_data': X_ipca_d,
'explained_variance_ratio': ipca_d.explained_variance_ratio_,
'cumulative_variance': np.sum(ipca_d.explained_variance_ratio_),
'reconstruction_error': error_ipca_d}
results_diff[dataset_name] = dataset_results
valid_methods_for_plot = {k: v for k, v in dataset_results.items() if
'transformed_data' in v and v['transformed_data'] is not None and
v['transformed_data'].shape[1] >= 2}
if not valid_methods_for_plot: print(f"数据集 {dataset_name} 没有足够的方法进行2D投影可视化。"); continue
fig_diff_data = plt.figure(figsize=(5 * len(valid_methods_for_plot), 5)); # 获取figure对象
plt.suptitle(f'数据集: {dataset_name} - 不同PCA变体的2D投影', fontsize=16)
for i, (method_name, method_res) in enumerate(valid_methods_for_plot.items()):
plt.subplot(1, len(valid_methods_for_plot), i + 1);
X_transformed_d = method_res['transformed_data']
plt.scatter(X_transformed_d[:, 0], X_transformed_d[:, 1], c=X_transformed_d[:, 0], cmap='viridis',
alpha=0.5)
title = f'{method_name}';
if 'cumulative_variance' in method_res and method_res.get(
'cumulative_variance') is not None and not np.isnan(
method_res['cumulative_variance']): title += f'\n解释方差: {method_res["cumulative_variance"]:.2f}'
if 'reconstruction_error' in method_res and method_res.get(
'reconstruction_error') is not None and not np.isnan(
method_res['reconstruction_error']): title += f'\nMSE: {method_res["reconstruction_error"]:.4f}'
plt.title(title);
plt.xlabel('主成分 1');
plt.ylabel('主成分 2');
plt.axis('square');
plt.grid(True, linestyle=':', alpha=0.5)
plt.tight_layout();
plt.subplots_adjust(top=0.85 if len(dataset_name) < 20 else 0.80)
plt.savefig(os.path.join(output_image_dir,
f"12_pca_on_dataset_{dataset_name.replace(' ', '_').replace('(', '').replace(')', '')}.png"))
plt.show()
plt.close(fig_diff_data)
return datasets, results_diff
pca_variants_on_different_datasets()
print("\n标准PCA执行完毕。所有图像已保存在 '{}' 目录中。".format(output_image_dir))
![]()
程序运行结果如下:
成功生成数据集 'PCA_dataset.csv',包含 300 个样本和 5 个特征。
数据集的前5行内容:
特征_1 特征_2 特征_3 特征_4 特征_5
0 11.206124 9.136486 4.428173 12.964414 10.017244
1 9.150353 7.617386 4.289509 12.005397 6.783859
2 11.879639 9.073098 5.883405 11.060705 6.335963
3 13.845953 11.243491 6.147410 11.631753 5.551980
4 9.734230 7.687871 4.942194 11.910430 4.176124
特征相关系数矩阵:
特征_1 特征_2 特征_3 特征_4 特征_5
特征_1 1.000000 0.919642 0.316386 0.044940 0.282763
特征_2 0.919642 1.000000 0.172895 0.167178 0.265318
特征_3 0.316386 0.172895 1.000000 -0.601832 0.121939
特征_4 0.044940 0.167178 -0.601832 1.000000 -0.021083
特征_5 0.282763 0.265318 0.121939 -0.021083 1.000000
![]()
由于数据集很大,这里只给出部分截图
![]()
程序运行结果如下:
![]()
![]()
![]()

![]()

![]()
![]()
![]()
![]()
六、总结
本文系统介绍了主成分分析(PCA)这一经典的无监督线性降维技术。首先阐述了PCA的核心目标:降维、特征提取、去相关、噪声过滤和数据可视化。然后详细讲解了PCA的数学基础,包括方差、协方差、协方差矩阵、特征值与特征向量等概念,以及完整的算法步骤:数据标准化→计算协方差矩阵→特征分解→排序并选择主成分→构建投影矩阵→数据降维。文章还对比了PCA的不同变体(稀疏PCA、核PCA、增量PCA)的优缺点和适用场景,并通过Python代码实现了数据生成、标准PCA分析、交互式可视化、重构误差评估、PCA变体比较等完整流程。最后指出PCA的局限性(线性假设、对异常值敏感等)和广泛应用领域(数据压缩、特征工程、图像处理等)。
更多推荐
 已为社区贡献10条内容
已为社区贡献10条内容







所有评论(0)