机器学习(五) 神经网络
机器学习(五) 神经网络1.单隐层神经网络1.1 从输入层到隐藏层连接输入层和隐藏层的是W1和b1。由X计算得到H十分简单,就是矩阵运算:H=X∗W1+b1H=X*W1+b1H=X∗W1+b11.2 从隐藏层到输出层连接隐藏层和输出层的是W2和b2。同样是通过矩阵运算进行的:Y=H∗W2+b2Y=H*W2+b2Y=H∗W2+b2通过上述两个线性方程的计算,我们就能得到最终的输出Y了,但是如果你还对
机器学习(五) 神经网络
1.单隐层神经网络
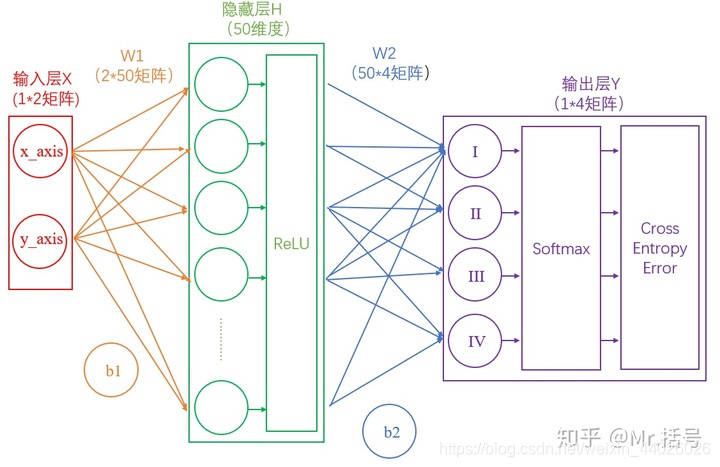
1.1 从输入层到隐藏层
连接输入层和隐藏层的是W1和b1。由X计算得到H十分简单,就是矩阵运算:
H=X∗W1+b1 H=X*W1+b1 H=X∗W1+b1
1.2 从隐藏层到输出层
连接隐藏层和输出层的是W2和b2。同样是通过矩阵运算进行的:
Y=H∗W2+b2 Y=H*W2+b2 Y=H∗W2+b2
通过上述两个线性方程的计算,我们就能得到最终的输出Y了,但是如果你还对线性代数的计算有印象的话,应该会知道:一系列线性方程的运算最终都可以用一个线性方程表示。也就是说,上述两个式子联立后可以用一个线性方程表达。对于两次神经网络是这样,就算网络深度加到100层,也依然是这样。这样的话神经网络就失去了意义。所以这里要对网络注入灵魂:激活层。
1.3 激活层
简而言之,激活层是为矩阵运算的结果添加非线性的。常用的激活函数有三种,分别是阶跃函数、Sigmoid和ReLU: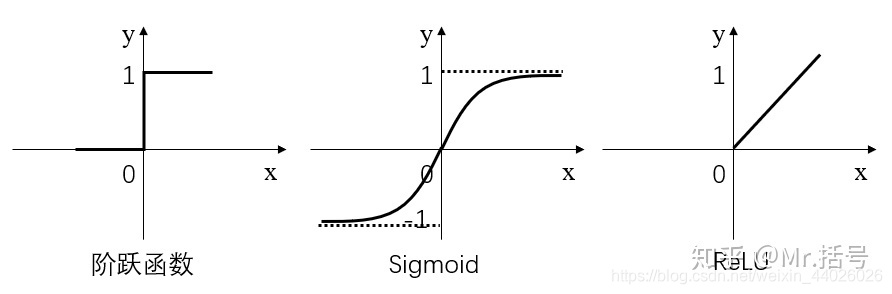
- 阶跃函数:当输入小于等于0时,输出0;当输入大于0时,输出1。
- Sigmoid:当输入趋近于正无穷/负无穷时,输出无限接近于1/0。
- ReLU:当输入小于0时,输出0;当输入大于0时,输出等于输入。
其中,阶跃函数输出值是跳变的,且只有二值,较少使用;
Sigmoid函数在当x的绝对值较大时,曲线的斜率变化很小(梯度消失),并且计算较复杂;
ReLU是当前较为常用的激活函数。
激活函数具体是怎么计算的呢?假如经过公式H=X*W1+b1计算得到的H值为:(1,-2,3,-4,7…),那么经过阶跃函数激活层后就会变为(1,0,1,0,1…),经过ReLU激活层之后会变为(1,0,3,0,7…)。需要注意的是,每个隐藏层计算(矩阵线性运算)之后,都需要加一层激活层,要不然该层线性计算是没有意义的。
1.4 输出的正规化
由上面分析可知,输出Y的值可能会是(3,1,0.1,0.5)这样的矩阵,诚然我们可以找到里边的最大值“3”,从而找到对应的分类为I,但是这并不直观。我们想让最终的输出为概率,也就是说可以生成像(90%,5%,2%,3%)这样的结果,这样做不仅可以找到最大概率的分类,而且可以知道各个分类计算的概率值。我们将使用这个计算公式做输出结果正规化处理的层叫做“Softmax”层。
计算公式如下:
Sj=eaj∑k=1Neak S_j=\frac{e^{a_j}}{\sum_{k=1}^N{e^{a_k}}} Sj=∑k=1Neakeaj
他能够保证:
所有的值都是 [0, 1] 之间的(因为概率必须是 [0, 1])所有的值加起来等于 1
从概率的角度解释 softmax 的话,就是:
Sj=P(y=j∣a) S_j=P\left( y=j|a \right) Sj=P(y=j∣a)
简单来说分三步进行:
(1)以e为底对所有元素求指数幂;
(2)将所有指数幂求和;
(3)分别将这些指数幂与该和做商。
这样求出的结果中,所有元素的和一定为1,而每个元素可以代表概率值。
1.5 如何衡量输出的好坏
通过Softmax层之后,我们得到了I,II,III和IV这四个类别分别对应的概率,但是要注意,这是神经网络计算得到的概率值结果,而非真实的情况。
比如,Softmax输出的结果是(90%,5%,3%,2%),真实的结果是(100%,0,0,0)。虽然输出的结果可以正确分类,但是与真实结果之间是有差距的,一个优秀的网络对结果的预测要无限接近于100%,为此,我们需要将Softmax输出结果的好坏程度做一个“量化”。一种直观的解决方法,是用1减去Softmax输出的概率,比如1-90%=0.1。
不过更为常用且巧妙的方法是,求对数的负数。还是用90%举例,对数的负数就是:-log0.9=0.046可以想见,概率越接近100%,该计算结果值越接近于0,说明结果越准确,该输出叫做“交叉熵损失(Cross Entropy Error)”。我们训练神经网络的目的,就是尽可能地减少这个“交叉熵损失”。
1.6 反向传播与参数优化
上面讲述了神经网络的正向传播过程。一句话总结一下:神经网络的传播都是形如Y=WX+b的矩阵运算;为了给矩阵运算加入非线性,需要在隐藏层中加入激活层;输出层结果需要经过Softmax层处理为概率值,并通过交叉熵损失来量化当前网络的优劣。算出交叉熵损失后,就要开始反向传播了。其实反向传播就是一个参数优化的过程,优化对象就是网络中的所有W和b(因为其他所有参数都是确定的)。神经网络的神奇之处,就在于它可以自动做W和b的优化,在深度学习中,参数的数量有时会上亿,不过其优化的原理和我们这个两层神经网络是一样的。
反向传播就是计算偏微分,信息会从神经网络的高层向底层反向传播,并在这个过程中根据输出来调整权重。反向传播的思路是拿到损失函数给出的值,从结果开始,顺藤摸瓜,逐步求导,偏微分逐步地发现每一个参数应该往哪个方向调整才能减小损失。
1.7 单隐层网络预测客户流失率
import numpy as np
import pandas as pd
df_bank = pd.read_csv('C:/Users/aaa/Desktop/python/data/BankCustomer.csv') #df表示这是一个Pandas Dataframe格式数据
df_bank.head()

# 把二元类别文本数字化
df_bank['Gender'].replace("Female",0,inplace = True)
df_bank['Gender'].replace("Male",1,inplace=True)
# 显示数字类别
print("Gender unique values",df_bank['Gender'].unique())
# 把多元类别转换成多个二元哑变量,然后贴回原始数据集
d_city = pd.get_dummies(df_bank['City'], prefix = "City") #one-hot编码
df_bank = [df_bank, d_city]
df_bank = pd.concat(df_bank, axis = 1)
# 构建特征和标签集合
y = df_bank ['Exited'] #Exited作y变量单拿出来
X = df_bank.drop(['Name', 'Exited','City'], axis=1)
X.head() #显示新的特征集

拆分数据集:
from sklearn.model_selection import train_test_split #拆分数据集
X_train, X_test, y_train, y_test = train_test_split(X, y,
test_size=0.2, random_state=0)
特征缩放:
#特征缩放
from sklearn.preprocessing import StandardScaler # 导入特征缩放器
sc = StandardScaler() # 特征缩放器
X_train = sc.fit_transform(X_train) # 拟合并应用于训练集
X_test = sc.transform (X_test) # 训练集结果应用于测试集
先尝试用逻辑回归做分析:
from sklearn.linear_model import LogisticRegression # 导入Sklearn模型
lr = LogisticRegression() # 逻辑回归模型
history = lr.fit(X_train,y_train) # 训练机器
print("逻辑回归测试集准确率 {:.2f}%".format(lr.score(X_test,y_test)*100))
单隐层网络keras实现:
- Dense是层的类型,代表密集层网络
- input_dim 是输入维度,输入维度必须与特征维度相同
- units是输出维度,该参数也可写为output_dim=12,甚至忽略参数名
- activation是激活函数,这是每一层都需要设置的参数
#单隐层神经网络的keras实现
import keras
from keras.models import Sequential #导入Keras序贯模型
from keras.layers import Dense #导入Keras全连接层
ann = Sequential() # 创建一个序贯ANN(Artifical Neural Network)模型
ann.add(Dense(units=12, input_dim=12, activation = 'relu')) # 添加输入层,需要指明下一层输出维度(也就是神经元的个人),输入维度,以及激活函数
ann.add(Dense(units=24, activation = 'relu')) # 添加隐层,自动接受输入,只需要指明输出维度以及激活函数
ann.add(Dense(units=1, activation = 'sigmoid')) # 添加输出层,对于二分类问题
ann.summary() # 显示网络模型(这个语句不是必须的)

显示神经网络图形:
from IPython.display import SVG #实现神经网络的图形化显示
from keras.utils.vis_utils import model_to_dot
SVG(model_to_dot(ann,show_shapes = True ).create(prog='dot', format='svg'))
# 编译神经网络,指定优化器,损失函数,以及评估标准
ann.compile(optimizer = 'adam', #优化器optimizer
loss = 'binary_crossentropy', #损失函数 loss
metrics = ['acc']) #评估指标metrics
开始训练:
深度学习模型不会同时处理整个数据集,而是将数据分成小批量,通过向量化计算方式进行处理。batch_size指定批量大小为64
history = ann.fit(X_train, y_train, # 指定训练集
epochs=30, # 指定训练的轮次
batch_size=64, # 指定数据批量
validation_data=(X_test, y_test)) #指定验证集,这里为了简化模型,直接用测试集数据进行验证
# 这段代码参考《Python深度学习》一书中的学习曲线的实现
def show_history(history): # 显示训练过程中的学习曲线
loss = history.history['loss']
val_loss = history.history['val_loss']
epochs = range(1, len(loss) + 1)
plt.figure(figsize=(12,4))
plt.subplot(1, 2, 1)
plt.plot(epochs, loss, 'bo', label='Training loss')
plt.plot(epochs, val_loss, 'b', label='Validation loss')
plt.title('Training and validation loss')
plt.xlabel('Epochs')
plt.ylabel('Loss')
plt.legend()
acc = history.history['acc']
val_acc = history.history['val_acc']
plt.subplot(1, 2, 2)
plt.plot(epochs, acc, 'bo', label='Training acc')
plt.plot(epochs, val_acc, 'b', label='Validation acc')
plt.title('Training and validation accuracy')
plt.xlabel('Epochs')
plt.ylabel('Accuracy')
plt.legend()
plt.show()
show_history(history) # 调用这个函数,并将神经网络训练历史数据作为参数输入
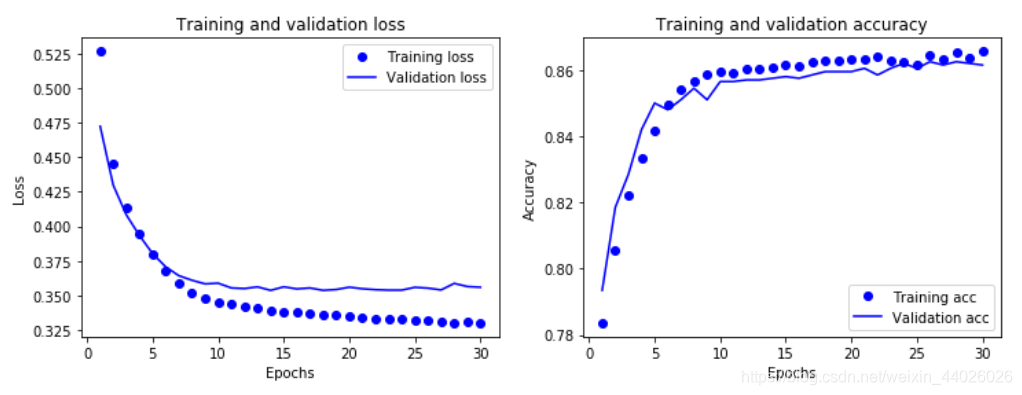
使用分类报告与混淆矩阵评价模型:
from sklearn.metrics import classification_report # 导入分类报告
def show_report(X_test, y_test, y_pred): # 定义一个函数显示分类报告
if y_test.shape != (2000,1):
y_test = y_test.values # 把Panda series转换成Numpy array
y_test = y_test.reshape((len(y_test),1)) # 转换成与y_pred相同的形状
print(classification_report(y_test,y_pred,labels=[0, 1])) #调用分类报告
from sklearn.metrics import confusion_matrix # 导入混淆矩阵
def show_matrix(y_test, y_pred): # 定义一个函数显示混淆矩阵
cm = confusion_matrix(y_test,y_pred) # 调用混淆矩阵
plt.title("ANN Confusion Matrix") # 标题
sns.heatmap(cm,annot=True,cmap="Blues",fmt="d",cbar=False) # 热力图设定
plt.show() # 显示混淆矩阵
y_pred = ann.predict(X_test,batch_size=10) # 预测测试集的标签
y_pred = np.round(y_pred) # 四舍五入,将分类概率值转换成0/1整数值
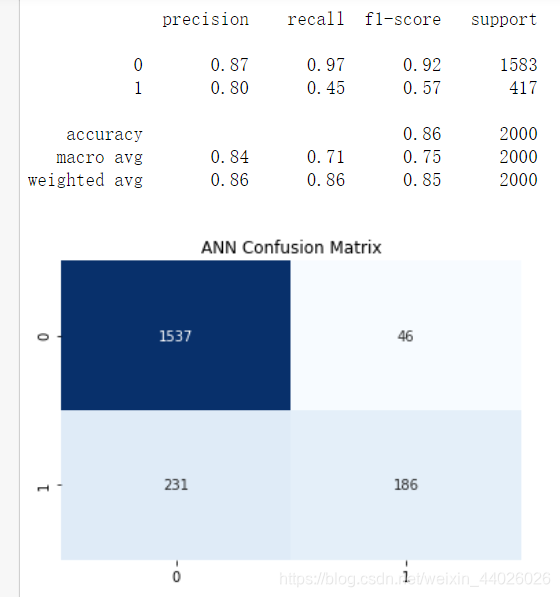
show_report(X_test, y_test, y_pred)
show_matrix(y_test, y_pred)
2. 用keras深度神经网络预测客户流失率
搭建多层神经网络,还是使用序贯模型:
#使用keras深度神经网络预测客户流失率
ann = Sequential() # 创建一个序贯ANN模型
ann.add(Dense(units=12, input_dim=12, activation = 'relu')) # 添加输入层
ann.add(Dense(units=24, activation = 'relu')) # 添加隐层
ann.add(Dense(units=48, activation = 'relu')) # 添加隐层
ann.add(Dense(units=96, activation = 'relu')) # 添加隐层
ann.add(Dense(units=192, activation = 'relu')) # 添加隐层
ann.add(Dense(units=1, activation = 'sigmoid')) # 添加输出层
# 编译神经网络,指定优化器,损失函数,以及评估指标
ann.compile(optimizer = 'RMSprop', # 优化器
loss = 'binary_crossentropy', # 损失函数
metrics = ['acc']) # 评估指标
history = ann.fit(X_train, y_train, # 指定训练集
epochs=30, # 指定训练的轮次
batch_size=64, # 指定数据批量
validation_data=(X_test, y_test)) # 指定验证集
y_pred = ann.predict(X_test,batch_size=10) # 预测测试集的标签
y_pred = np.round(y_pred) # 将分类概率值转换成0/1整数值
show_history(history)
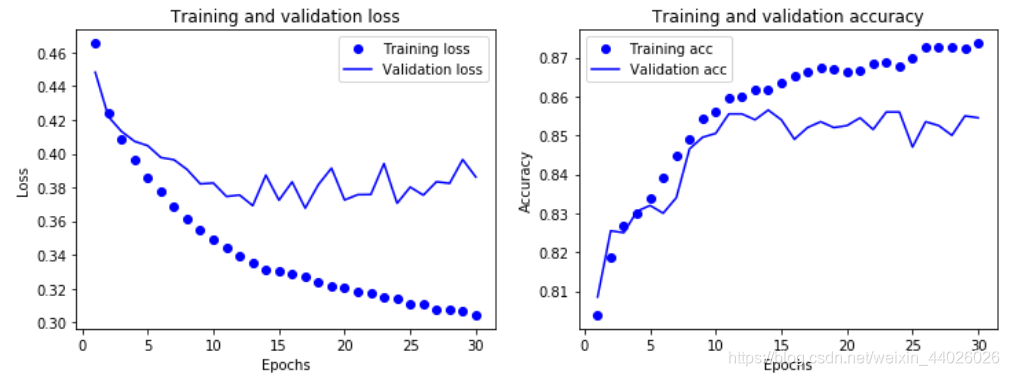
随着轮次的增加,训练的误差值逐渐减小,但是验证集上的损失波动很大,也就是说网络的参数逐渐对训练集的数据形成了过高的适应性,开始出现过拟合现象。
show_report(X_test, y_test, y_pred)
show_matrix(y_test, y_pred)
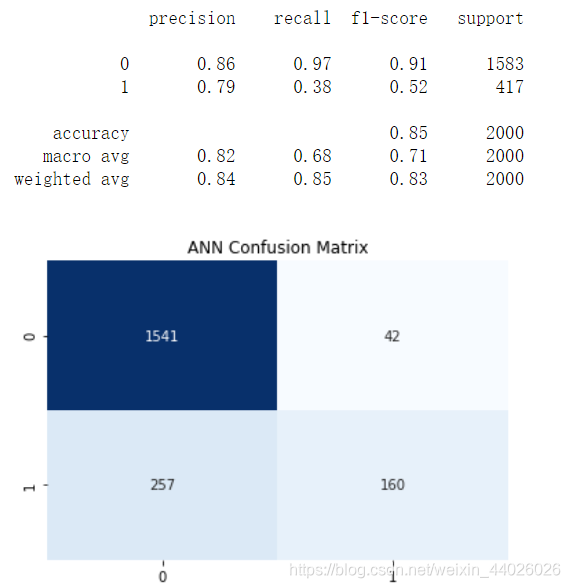
F1分数只有0.52反而不如单隐层网络。
2.1神经网络正则化:添加dropout层
#神经网络正则化:添加dropout层来解决神经网络过拟合问题
#dropout层即随机将该层的一部分神经元的输出特征丢掉(设为0),相当于随机消灭一部分神经元
from keras.layers import Dropout # 导入Dropout
ann = Sequential() # 创建一个序贯ANN模型
ann.add(Dense(units=12, input_dim=12, activation = 'relu')) # 添加输入层
ann.add(Dense(units=24, activation = 'relu')) # 添加隐层
ann.add(Dropout(0.5)) # 添加Dropout
ann.add(Dense(units=48, activation = 'relu')) # 添加隐层
ann.add(Dropout(0.5)) # 添加Dropout
ann.add(Dense(units=96, activation = 'relu')) # 添加隐层
ann.add(Dropout(0.5)) # 添加Dropout
ann.add(Dense(units=192, activation = 'relu')) # 添加隐层
ann.add(Dropout(0.5)) # 添加Dropout
ann.add(Dense(units=1, activation = 'sigmoid')) # 添加输出层
ann.compile(optimizer = 'adam', # 优化器
loss = 'binary_crossentropy', #损失函数
metrics = ['acc']) # 评估指标
history = ann.fit(X_train, y_train, epochs=30, batch_size=64, validation_data=(X_test, y_test))
y_pred = ann.predict(X_test,batch_size=10) # 预测测试集的标签
y_pred = np.round(y_pred) # 将分类概率值转换成0/1整数值
show_history(history)
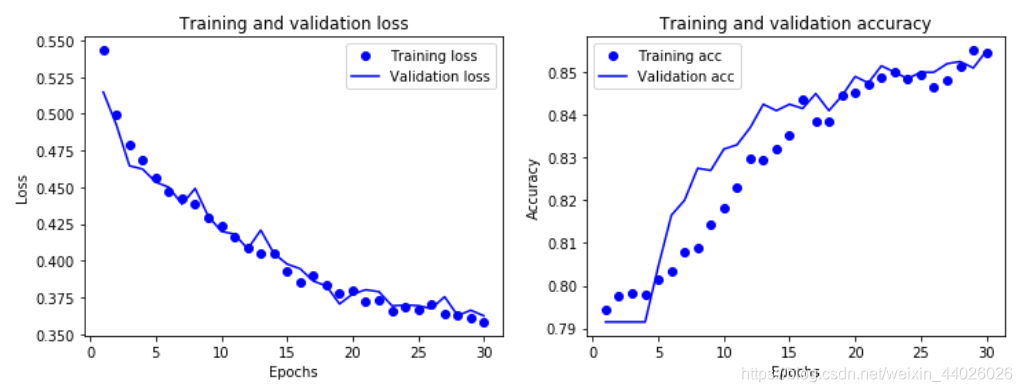
可见添加dropout层后,过拟合现象被大幅度抑制了。
show_report(X_test, y_test, y_pred)
show_matrix(y_test, y_pred)
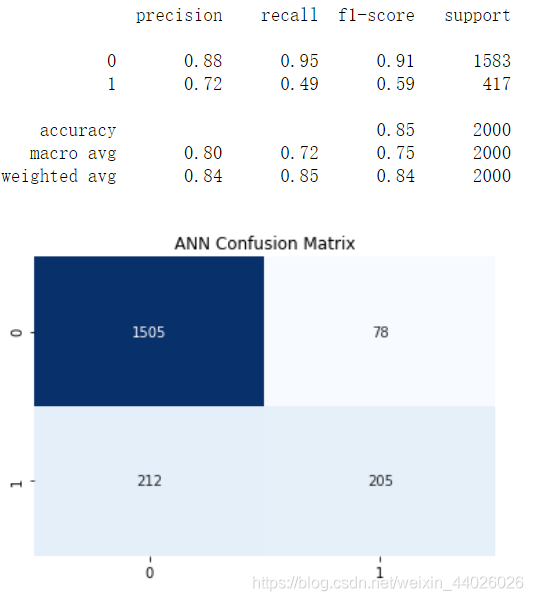
更多推荐
 已为社区贡献5条内容
已为社区贡献5条内容







所有评论(0)