引言：当代码遇见美学

在计算机科学的世界里，数组是最基础却也是最强大的数据结构之一。它如同数字世界中的容器，承载着信息的排列与组合。今天，我们将深入探索两个看似简单却蕴含深意的数组操作问题：移除有序数组中的重复项和寻找下一个排列。这两个问题不仅考验着我们对算法效率的把握，更揭示了数据组织中隐藏的规律与美感。

想象一下，你是一位数字艺术家，面对着一排杂乱无章的数字，你的任务是将它们重新排列，创造出既符合规则又具有美感的组合。这不仅仅是技术问题，更是一种艺术形式——一种通过代码表达的数字美学。

第一章：有序数组的唯一化之旅

题目：
给你一个 非严格递增排列 的数组 nums ，请你 原地 删除重复出现的元素，使每个元素 只出现一次 ，返回删除后数组的新长度。元素的 相对顺序 应该保持 一致 。然后返回 nums 中唯一元素的个数。

考虑 nums 的唯一元素的数量为 k ，你需要做以下事情确保你的题解可以被通过：

更改数组 nums ，使 nums 的前 k 个元素包含唯一元素，并按照它们最初在 nums 中出现的顺序排列。nums 的其余元素与 nums 的大小不重要。
返回 k 。
判题标准:

系统会用下面的代码来测试你的题解:

int[] nums = [...]; // 输入数组
int[] expectedNums = [...]; // 长度正确的期望答案

int k = removeDuplicates(nums); // 调用

assert k == expectedNums.length;
for (int i = 0; i < k; i++) {
    assert nums[i] == expectedNums[i];
}
如果所有断言都通过，那么您的题解将被 通过。

问题解析与直观理解

给定一个按非严格递增排列的整数数组，我们的任务是原地移除所有重复出现的元素，使得每个元素只出现一次，并保持相对顺序。最终返回唯一元素的数量。

这个问题的核心挑战在于"原地"操作——我们不能使用额外的数组空间，必须在原始数组上直接修改。这就像是在不移动家具的情况下重新整理房间，需要巧妙的策略和精确的操作。

def removeDuplicates(nums):
    if not nums:
        return 0
    
    # 慢指针，指向当前唯一序列的末尾
    slow = 0
    
    # 快指针，遍历整个数组
    for fast in range(1, len(nums)):
        if nums[fast] != nums[slow]:
            slow += 1
            nums[slow] = nums[fast]
    
    return slow + 1

双指针法：优雅的舞蹈

上述解决方案采用了经典的"双指针"技术，这是处理数组原地操作问题的利器。让我们深入剖析这个算法的精妙之处：

• 慢指针（slow）：代表着"已处理区域"的边界，始终指向当前唯一序列的最后一个元素

• 快指针（fast）：探索者角色，遍历整个数组，寻找新的唯一元素

这两个指针如同在数组上演绎一场精心编排的舞蹈：快指针不断前进探索新领域，当发现与慢指针不同的元素时，慢指针向前一步并接纳这个新元素。

示例 1：

输入：nums = [1,1,2]
输出：2, nums = [1,2,_]
解释：函数应该返回新的长度 2 ，并且原数组 nums 的前两个元素被修改为 1, 2 。不需要考虑数组中超出新长度后面的元素。
示例 2：

输入：nums = [0,0,1,1,1,2,2,3,3,4]
输出：5, nums = [0,1,2,3,4]
解释：函数应该返回新的长度 5 ， 并且原数组 nums 的前五个元素被修改为 0, 1, 2, 3, 4 。不需要考虑数组中超出新长度后面的元素。

题目程序：

#include <stdio.h>  // 包含标准输入输出头文件，用于printf等函数

// 函数功能：原地删除有序数组中的重复元素
// 参数说明：nums - 整数数组指针，numsSize - 数组大小
// 返回值：唯一元素的数量
int removeDuplicates(int* nums, int numsSize) {
    // 处理空数组的特殊情况
    if (numsSize == 0) {
        return 0;  // 数组为空直接返回0
    }
    
    int slow = 0;  // 慢指针，指向当前唯一序列的最后一个位置
    
    // 快指针从第二个元素开始遍历（索引1）
    for (int fast = 1; fast < numsSize; fast++) {
        // 当快指针指向的元素与慢指针指向的元素不同时
        if (nums[fast] != nums[slow]) {
            slow++;  // 慢指针向前移动一位
            nums[slow] = nums[fast];  // 将快指针的元素复制到慢指针位置
        }
        // 如果元素相同，快指针继续前进，慢指针保持不变
    }
    
    return slow + 1;  // 返回唯一元素个数（索引slow+1）
}

int main() {
    // 测试用例1
    int nums1[] = {1, 1, 2};  // 初始化测试数组
    int expectedNums1[] = {1, 2};  // 期望结果数组
    int k1 = removeDuplicates(nums1, 3);  // 调用去重函数
    
    // 验证结果
    printf("测试1 - 唯一元素数量: %d\n", k1);
    printf("当前数组: [");
    for (int i = 0; i < k1; i++) {
        printf("%d", nums1[i]);
        if (i < k1 - 1) printf(", ");
    }
    printf("]\n");
    
    // 测试用例2
    int nums2[] = {0, 0, 1, 1, 1, 2, 2, 3, 3, 4};
    int expectedNums2[] = {0, 1, 2, 3, 4};
    int k2 = removeDuplicates(nums2, 10);
    
    printf("测试2 - 唯一元素数量: %d\n", k2);
    printf("当前数组: [");
    for (int i = 0; i < k2; i++) {
        printf("%d", nums2[i]);
        if (i < k2 - 1) printf(", ");
    }
    printf("]\n");
    
    return 0;  // 程序正常退出
}

输出结果：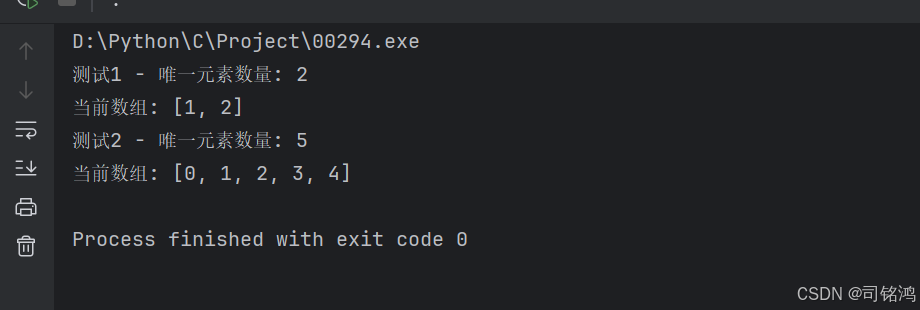

算法复杂度分析

• 时间复杂度：O(n)，其中n是数组的长度。我们只需要遍历数组一次

• 空间复杂度：O(1)，只使用了常数额外空间

这种高效性使得算法即使面对最大规模的输入（3 * 10^4个元素）也能轻松应对。

实际应用场景

数组去重在实际开发中有着广泛的应用：

• 数据库查询结果去重

• 日志数据分析中去除重复条目

• 机器学习特征工程中的特征唯一化

• 大数据处理中的预处理步骤

第二章：排列的字典序与下一个排列

题目：
整数数组的一个 排列  就是将其所有成员以序列或线性顺序排列。

例如，arr = [1,2,3] ，以下这些都可以视作 arr 的排列：[1,2,3]、[1,3,2]、[3,1,2]、[2,3,1] 。
整数数组的 下一个排列 是指其整数的下一个字典序更大的排列。更正式地，如果数组的所有排列根据其字典顺序从小到大排列在一个容器中，那么数组的 下一个排列 就是在这个有序容器中排在它后面的那个排列。如果不存在下一个更大的排列，那么这个数组必须重排为字典序最小的排列（即，其元素按升序排列）。

例如，arr = [1,2,3] 的下一个排列是 [1,3,2] 。
类似地，arr = [2,3,1] 的下一个排列是 [3,1,2] 。
而 arr = [3,2,1] 的下一个排列是 [1,2,3] ，因为 [3,2,1] 不存在一个字典序更大的排列。
给你一个整数数组 nums ，找出 nums 的下一个排列。

必须 原地 修改，只允许使用额外常数空间。

排列的数学之美

在深入问题之前，让我们先理解什么是排列的字典序。字典序类似于单词在字典中的排列顺序：比较两个序列时，从第一个元素开始，如果相同则比较下一个，直到找到差异。

例如，对于[1,2,3]的所有排列按字典序排列为：
[1,2,3], [1,3,2], [2,1,3], [2,3,1], [3,1,2], [3,2,1]

问题解析：寻找下一个排列

给定一个整数数组，找出其下一个排列（即字典序比当前排列大的最小排列）。如果当前已经是最大排列，则返回最小排列。

这个问题要求我们必须原地修改数组，且只能使用常数额外空间。这就像是要解开一个数字谜题，需要找到隐藏在排列中的规律。

算法洞察与解决方案

经过数学分析，我们发现下一个排列可以通过以下步骤找到：

1. 从后向前查找第一个相邻元素对(i, i+1)，满足nums[i] < nums[i+1]

2. 如果找不到这样的对，说明当前是最大排列，直接反转整个数组

3. 从后向前查找第一个元素j，满足nums[j] > nums[i]

4. 交换nums[i]和nums[j]

5. 反转从位置i+1到数组末尾的部分

def nextPermutation(nums):
    """
    寻找数组的下一个排列（原地修改）
    """
    n = len(nums)
    if n <= 1:
        return
    
    # 步骤1：从后向前找到第一个下降点
    i = n - 2
    while i >= 0 and nums[i] >= nums[i+1]:
        i -= 1
    
    # 如果找到下降点
    if i >= 0:
        # 步骤2：从后向前找到第一个大于nums[i]的元素
        j = n - 1
        while j >= 0 and nums[j] <= nums[i]:
            j -= 1
        # 步骤3：交换这两个元素
        nums[i], nums[j] = nums[j], nums[i]
    
    # 步骤4：反转下降点之后的部分
    left, right = i+1, n-1
    while left < right:
        nums[left], nums[right] = nums[right], nums[left]
        left += 1
        right -= 1

算法原理深度解析

这个算法的美妙之处在于它深刻理解了排列的字典序结构：

1. 寻找下降点：字典序增加的关键在于找到一个可以增大的位置。从右向左找第一个下降点，意味着这个点右侧是一个递减序列（已经是这部分能表示的最大值）

2. 交换适当元素：将下降点与右侧刚好大于它的元素交换，这样保证了增大幅度最小

3. 反转右侧：交换后右侧仍然是递减序列，反转后变成递增序列，使这部分表示最小值

这个过程就像是在数字游戏中寻找下一个密码组合，既需要系统性思维，又需要对数字规律的敏锐直觉。

示例 1：

输入：nums = [1,2,3]
输出：[1,3,2]
示例 2：

输入：nums = [3,2,1]
输出：[1,2,3]
示例 3：

输入：nums = [1,1,5]
输出：[1,5,1]

题目程序：

#include <stdio.h>  // 包含标准输入输出头文件，用于printf函数

// 函数功能：交换两个整数的值
// 参数说明：a - 第一个整数的指针，b - 第二个整数的指针
void swap(int* a, int* b) {
    int temp = *a;  // 创建临时变量存储a的值
    *a = *b;        // 将b的值赋给a
    *b = temp;      // 将临时变量（原a的值）赋给b
}

// 函数功能：反转数组中指定范围的元素
// 参数说明：nums - 整数数组指针，start - 起始索引，end - 结束索引
void reverse(int* nums, int start, int end) {
    // 使用双指针从两端向中间遍历并交换元素
    while (start < end) {  // 当起始索引小于结束索引时继续循环
        swap(&nums[start], &nums[end]);  // 交换起始和结束位置的元素
        start++;  // 起始索引向右移动
        end--;    // 结束索引向左移动
    }
}

// 函数功能：寻找并实现数组的下一个排列（原地修改）
// 参数说明：nums - 整数数组指针，numsSize - 数组大小
void nextPermutation(int* nums, int numsSize) {
    // 步骤1：从后向前查找第一个相邻元素对(i, i+1)，满足nums[i] < nums[i+1]
    int i = numsSize - 2;  // 从倒数第二个元素开始向前查找
    while (i >= 0 && nums[i] >= nums[i + 1]) {  // 当前元素大于等于后一个元素时继续向前
        i--;  // 向前移动索引
    }
    
    // 如果找到了下降点（i >= 0）
    if (i >= 0) {
        // 步骤2：从后向前查找第一个大于nums[i]的元素
        int j = numsSize - 1;  // 从最后一个元素开始向前查找
        while (j >= 0 && nums[j] <= nums[i]) {  // 当前元素小于等于nums[i]时继续向前
            j--;  // 向前移动索引
        }
        // 步骤3：交换nums[i]和nums[j]
        swap(&nums[i], &nums[j]);
    }
    
    // 步骤4：反转从位置i+1到数组末尾的部分
    // 如果没找到下降点（i = -1），则反转整个数组（得到最小排列）
    reverse(nums, i + 1, numsSize - 1);  // 反转i+1到末尾的部分
}

// 函数功能：打印数组元素
// 参数说明：nums - 整数数组指针，size - 数组大小
void printArray(int* nums, int size) {
    printf("[");  // 输出左括号
    for (int i = 0; i < size; i++) {  // 遍历数组元素
        printf("%d", nums[i]);  // 输出当前元素
        if (i < size - 1) {  // 如果不是最后一个元素
            printf(", ");  // 输出逗号和空格
        }
    }
    printf("]");  // 输出右括号
}

int main() {
    // 测试用例1
    int nums1[] = {1, 2, 3};  // 初始化测试数组1
    int size1 = sizeof(nums1) / sizeof(nums1[0]);  // 计算数组1的大小
    printf("原始数组: ");
    printArray(nums1, size1);  // 打印原始数组
    printf("\n");
    
    nextPermutation(nums1, size1);  // 调用下一个排列函数
    
    printf("下一个排列: ");
    printArray(nums1, size1);  // 打印结果数组
    printf("\n\n");
    
    // 测试用例2
    int nums2[] = {3, 2, 1};  // 初始化测试数组2
    int size2 = sizeof(nums2) / sizeof(nums2[0]);  // 计算数组2的大小
    printf("原始数组: ");
    printArray(nums2, size2);  // 打印原始数组
    printf("\n");
    
    nextPermutation(nums2, size2);  // 调用下一个排列函数
    
    printf("下一个排列: ");
    printArray(nums2, size2);  // 打印结果数组
    printf("\n\n");
    
    // 测试用例3
    int nums3[] = {1, 1, 5};  // 初始化测试数组3
    int size3 = sizeof(nums3) / sizeof(nums3[0]);  // 计算数组3的大小
    printf("原始数组: ");
    printArray(nums3, size3);  // 打印原始数组
    printf("\n");
    
    nextPermutation(nums3, size3);  // 调用下一个排列函数
    
    printf("下一个排列: ");
    printArray(nums3, size3);  // 打印结果数组
    printf("\n\n");
    
    // 测试用例4
    int nums4[] = {1, 3, 2};  // 初始化测试数组4
    int size4 = sizeof(nums4) / sizeof(nums4[0]);  // 计算数组4的大小
    printf("原始数组: ");
    printArray(nums4, size4);  // 打印原始数组
    printf("\n");
    
    nextPermutation(nums4, size4);  // 调用下一个排列函数
    
    printf("下一个排列: ");
    printArray(nums4, size4);  // 打印结果数组
    printf("\n");
    
    return 0;  // 程序正常退出
}

输出结果：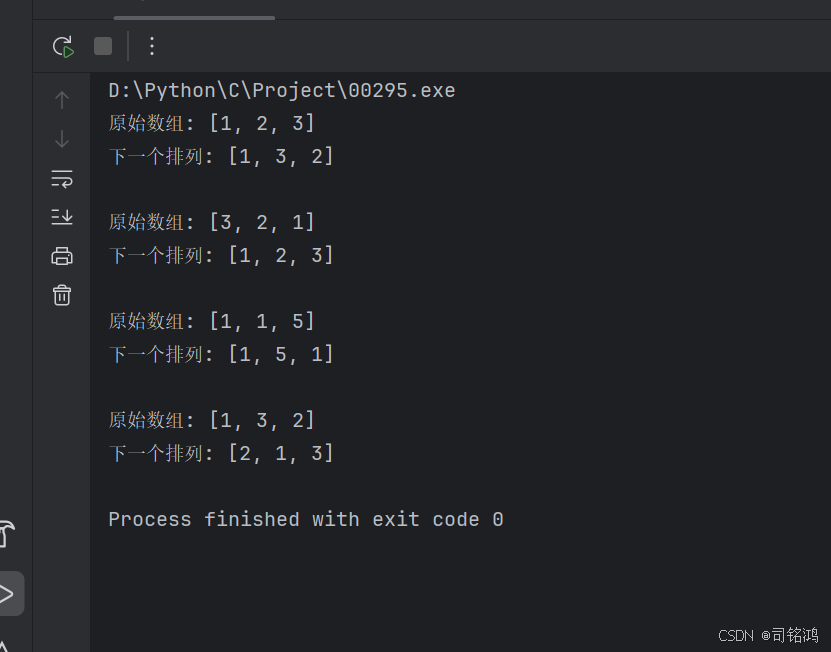

实际应用价值

下一个排列算法在多个领域有重要应用：

• 组合优化问题中的解空间遍历

• 密码学中的密钥生成

• 游戏开发中的关卡组合生成

• 测试用例的自动化生成

第三章：算法思维的艺术与科学

从具体到抽象：算法设计的哲学

通过分析这两个问题，我们可以提炼出一些通用的算法设计原则：

1. 空间约束下的创造力：原地操作要求我们充分发挥想象力，在有限空间中找到高效解决方案

2. 指针的魔力：双指针技术是处理数组问题的强大工具，能够在不增加空间复杂度的情况下提高效率

3. 发现隐藏模式：许多算法问题都隐藏着数学模式或结构，发现这些模式是解决问题的关键

算法优化思维框架

面对一个新问题时，我们可以遵循以下思维框架：

1. 暴力法首先：先思考最直接的解决方案，理解问题本质

2. 识别冗余计算：分析暴力法中的重复计算或不必要操作

3. 寻找模式与结构：发现输入数据中的隐藏模式或数学结构

4. 应用已知范式：考虑是否可以使用已知算法范式（如双指针、贪心、动态规划等）

5. 优化与调整：根据问题特性调整和优化现有范式

第四章：代码实现的细节与技巧

边界情况处理

在实际编码中，边界情况的处理往往决定算法的鲁棒性：

python

# 移除重复元素中的边界情况处理
def removeDuplicates(nums):
    # 空数组处理
    if not nums:
        return 0
    # 单元素数组处理
    if len(nums) == 1:
        return 1
    
    # 主算法逻辑
    slow = 0
    for fast in range(1, len(nums)):
        if nums[fast] != nums[slow]:
            slow += 1
            nums[slow] = nums[fast]
    
    return slow + 1

测试用例设计

全面的测试用例是保证算法正确性的关键：

python

# 测试移除重复元素算法
def test_removeDuplicates():
    # 常规测试
    nums1 = [1,1,2]
    assert removeDuplicates(nums1) == 2
    assert nums1[:2] == [1,2]
    
    # 无重复测试
    nums2 = [1,2,3]
    assert removeDuplicates(nums2) == 3
    assert nums2 == [1,2,3]
    
    # 全重复测试
    nums3 = [1,1,1]
    assert removeDuplicates(nums3) == 1
    assert nums3[:1] == [1]
    
    # 空数组测试
    assert removeDuplicates([]) == 0
    
    print("所有测试通过!")

第五章：从算法到实际工程的跨越

性能考量与大规模数据处理

当我们将这些算法应用于实际工程场景时，需要考虑更多因素：

1. 内存访问模式：原地算法通常具有良好的缓存局部性，这在现代计算机架构中至关重要

2. 并行化潜力：分析算法是否可以被并行化以处理更大规模数据

3. 稳定性要求：在某些场景下，需要保持元素的相对顺序（如移除重复元素算法）

4. 数据类型适应性：算法是否适用于不同的数据类型（整数、浮点数、字符串等）

算法扩展与变种

这两个基础问题有许多有趣的变种：

1. 允许最多重复k次：修改移除重复元素算法，允许每个元素最多出现k次

2. 从前向后移除重复：尝试从前向后而不是从后向前寻找下一个排列

3. 第k个排列：直接计算第k个字典序排列，而不需要逐个生成

4. 带约束的排列：在特定约束条件下生成下一个排列

结语：算法的艺术与未来

通过深入探索数组唯一化和排列变换这两个经典问题，我们不仅掌握了具体的算法技巧，更领略了算法设计的艺术之美。这些看似简单的问题背后，蕴含着深刻的计算机科学原理和数学智慧。

在人工智能和大数据时代，这些基础算法思想以新的形式继续发挥着重要作用。从推荐系统的排序算法到自然语言处理的序列建模，从数据库查询优化到机器学习特征工程，算法思维始终是技术创新的核心驱动力。

正如计算机科学家Donald Knuth所说："算法是计算机科学的灵魂"。掌握算法不仅是为了解决技术问题，更是为了培养一种系统化、结构化的思维方式，这种思维方式能够帮助我们在复杂问题中找到优雅的解决方案。

无论你是初学者还是经验丰富的开发者，希望这篇深入浅出的探索能够激发你对算法之美的欣赏，并在你的编程之旅中提供新的启示和动力。记住，每一个复杂的系统都是由简单的算法构建而成，掌握这些基础构建块，你就能创造出令人惊叹的技术作品。