机器学习概念基本介绍

什么是机器学习？

Arthur Samuel 所定义的机器学习，是专指这种非显著式编程的方式。机器学习是这样的领域，它赋予计算机学习的能力，（这种学习能力）是通过非显著式编程获得的。

机器学习分类：监督学习（Supervised Learning）强化学习（Reinforcement Learning）

(1) 监督学习(Supervised Learning)：所有的经验都是人为搜集起来并输入计算机的，最终为训练数据打上标签或者进行预测。例如识别垃圾邮件、人脸识别、图像识别、天气预测、污染物浓度预测等。

若我们欲预测的是离散值，例如“垃圾邮件”和“正常邮件”，此类学习任务称为“分类”；若欲预测的是连续值，例如污染物浓度1.5%,4.8%，此类学习任务称为“回归”。

传统的监督学习包括支持向量机SVM(Support Vector Machine)、人工神经网络、深度神经网络DNN(Deep Neutral Network)

(2) 无监督学习(Unsupervised Learning)：只有特征，但是没有标签，即给定数据，‘寻找隐藏/潜在的结构和信息，进行分类。例如聚类、社交网络分析、群体分类。

无监督学习算法包括聚类、EM算法、主成分分析

(3) 半监督学习(Semi-supervised Learning)：由于标注数据是成本巨大的工程，因此，利用少量标注的数据和大量未标注的数据一起训练出一个更好的机器学习方法，即半监督学习算法，是一种趋势。

(4) 强化学习(Reinforcement Learning)：计算机通过与环境的互动，逐渐强化自己的行为模式，从而实现最大化收益的学习过程称为强化学习。

什么叫“显著式编程”？

举例说明，告诉计算机，黄色代表菊花，红色代表玫瑰花。那么，计算机识别到黄色就表示菊花，识别到红色就表示玫瑰花。

什么叫“非显著式编程”？

举例说明，事先并不约束计算机必须总结出什么规律，让计算机自己挑出最能区分菊花和玫瑰的一些规律。

显著式编程的劣势？

举例说明，让机器人冲咖啡，人类先把机器人所处环境调查清楚，然后规定机器人的活动路径。

非显著式编程的优势？

答：举例说明，让机器人冲咖啡，人类规定机器人可以采取一系列行为，规定机器人在特定的环境下做这些行为所带来的收益称为 “ 收益函数 ” 。

如：机器人自己摔倒，收益函数为负值；机器人自己摔倒，收益函数为负值；机器人自己取到咖啡，收益函数值为正值。

我们规定了行为和收益函数后，让计算机自己去找最大化收益函数的行为，一开始，计算机采用随机化的行为，但是，只要人类的程序编的足够好，计算机是可能找到一个最大化收益函数的行为模式的。

非显著式编程，使计算机通过数据、经验自动的学习，完成我人类交给的任务。

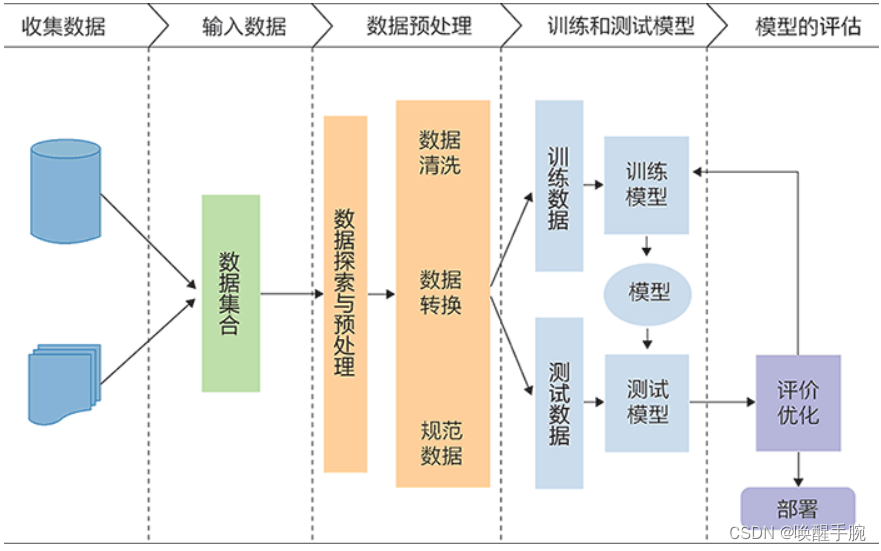
机器学习的步骤

（1）特征提取(Feature Extraction)：是指通过训练样本获得的，对机器学习任务有帮助的多个维度特征数据。

（2）特征选择(Feature Selection)，即对特征进行取舍。

（3）如何基于特征构建算法。（比如采用支持向量机）

机器学习的重点不是研究如何提取特征，而是假设在已经提取好特征的前提下，如何构造算法获得更好的性能指标。所以机器学习是假设已经在获得特征的前提下，研究合理的算法，使学习系统获得较好的性能。

Tom Mitshell 对机器学习的定义？

答：一个计算机程序被称为可以学习，是指它能够针对某个任务T和某个性能指标P，从经验E中学习。这种学习的特点是，它在T上的被P所衡量的性能，会随着经验E的增加而提高。

知识科普

线性可分：(Linear Separable)在二维空间中使用一条直线就可以将其区分开，三维空间中使用的是平面将其区分开，四维以及四维以上的空间使用的是超平面。

机器学习算法过程

基于SVM的尿沉渣红、白细胞识别：任务：识别尿沉淀物中的红细胞和白细胞；下图是标注过的训练样本，左边是白细胞，右边是红细胞；

在这个任务中，当我们拿到数据之后，构建机器学习算法的第一步：是观察数据，总结规律。

最近几年由于大数据和深度学习的发展，很多人会认为，只要收集足够多的数据，从网上随便下载一个开源的算法模型，直接将数据丢到算法模型中去训练，就可能获得很好的结果，这样的观点在大多数时候不正确，偶尔可能正确也是误打误撞的结果。如果我们自身对数据没有认知，我们很难设计出好的算法，也很难估计算法可能达到的性能极限。

特征提取（Feature Extraction）

仔细观察，图中左边的白细胞和右边的红细胞有什么区别呢？有可能被观察到的区别：

1.平均来说，白细胞面积比红细胞大；
2.白细胞没有红细胞圆；
3.白细胞内部纹理比红细胞粗糙。

机器学习的第一步是特征提取（Feature Extraction）；特征提取：通过训练样本获得的，对机器学习任务有帮助的多纬度特征数据。

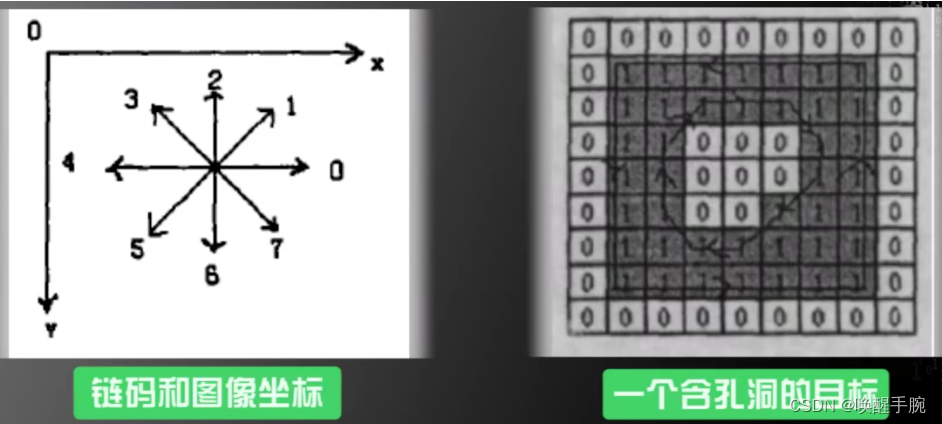
采用图像处理中的链码，来提取细胞的边缘信息，从细胞的边缘信息来推测出细胞的周长和面积，同时又基于边缘的信息，用图像处理中的哈夫（Hough）变换，提取细胞的圆形程度，接着又利用灰度共生矩阵，提取细胞的粗糙程度。

特征选择（Feature Selection）

在提取特征这一步做完后，下一步是对特征进行取舍，称为特征选择。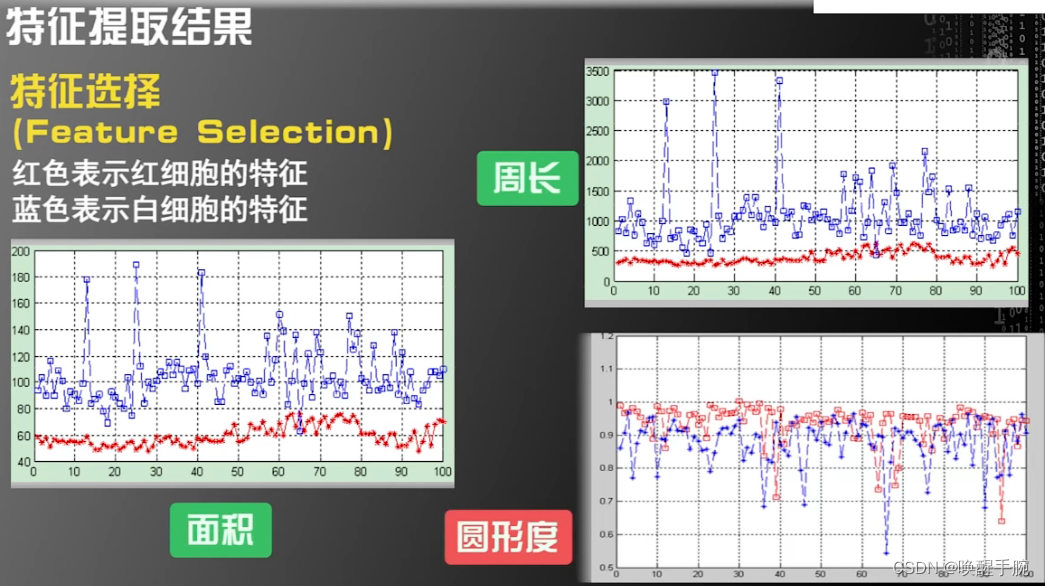

红色表示红细胞的特征，蓝色表示白细胞的特征，红细胞和白细胞每个样例对应的特征值。由周长和面积图可知，区分白细胞和红细胞的准确度是非常高的，因为蓝色的线和红色的线重合的地方很少；在圆形度这个特征上，尽管红细胞的平均值要高一些，但是红细胞的圆形度和白细胞的圆形度重合的地方还是很多的；因此我们若是只采用圆形度作为区分红细胞和白细胞的特征，识别度不会特别的高。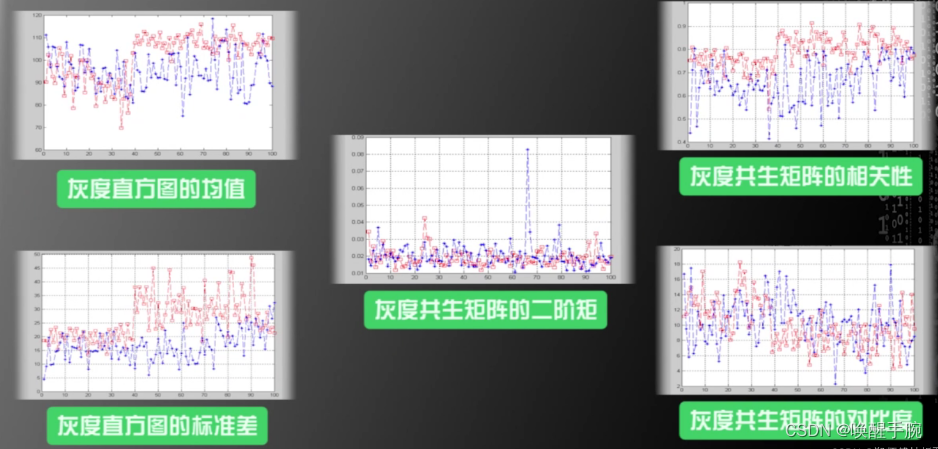

以上这五个灰度XX的特征区分度也不是很高。所以，最终决定，选择面积和周长作为区分白细胞和红细胞的特征，来构建机器学习系统。

机器学习第三步：如何基于这两个特征构建算法？

（1）支持向量机（SUPPORT VECTOR MACHINE）

此处用到了支持向量机的三种内核：线性内核、多项式核、高斯径向基函数核（可以将这三种内核看成是三种不同的机器学习算法）

（2）（对训练结果的处理）将所有的白细胞和红细胞画到一张二维的图上。

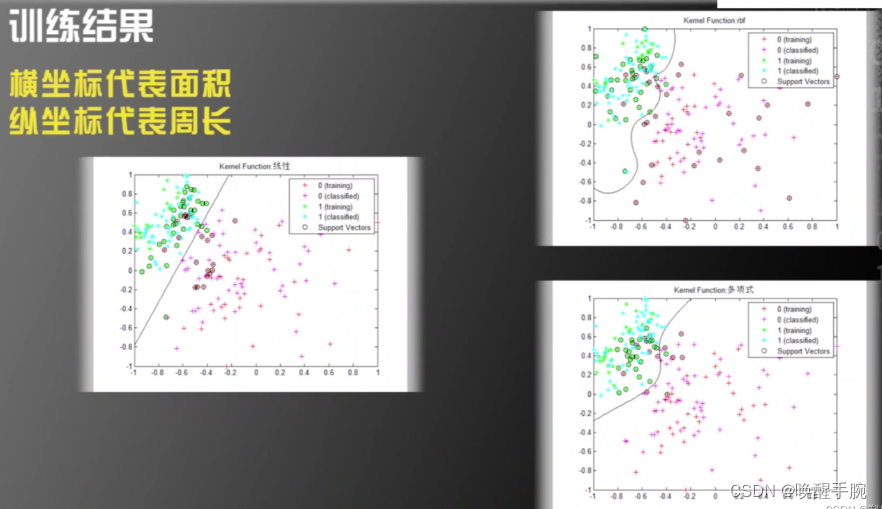
此例子中，就提取了面积和周长两个特征，特征空间是二维的，只有面积和周长两个维度，所以能很容易发现其规律，并画出来曲线；但是，若是特征空间的维度极高，例如我们提取了上万个特征，产生了上万维的特征空间，这规律就不好看出来了。

在最近流行的深度学习算法模型中，特征空间经常是几万维，甚至几十万维的，人眼对于超过三维的世界缺乏想象力，人看不到。但是，目前的机器学习算法，在处理高维特征空间方面，表现出优异的性能，远远超越了人类对于高维空间的想象。哪怕是对于上万维的空间，机器学习也可以给出一个预测的结果，而且这个结果在很多时候，还那么的准确。

支持向量机（SVM）原理

支持向量机（SVM）是一类按监督学习方式对数据进行二元分类的广义线性分类器，其决策边界是对学习样本求解的最大边距超平面，可以将问题化为一个求解凸二次规划的问题。与逻辑回归和神经网络相比，支持向量机，在学习复杂的非线性方程时提供了一种更为清晰，更加强大的方式。

具体来说就是在线性可分时，在原空间寻找两类样本的最优分类超平面。在线性不可分时，加入松弛变量并通过使用非线性映射将低维度输入空间的样本映射到高维度空间使其变为线性可分，这样就可以在该特征空间中寻找最优分类超平面。

原理举例说明

原理举例：$w^T$ 取 $(w_1,w_2{)}^T$，$x$ 取$(x1,x2{)}^T$， 则原式得 $w_1{x}_1+w_2{x}_2+b=0$ 与传统直线 $Ax+By+c=0$ 方程式相同，由二维三维空间推到更高维平面的一般式即为上式。

W：为平面法向量，决定了超平面的方向
b: 决定了超平面距原点的距离

法向量与样本属性的个数、超空间维数相同。在超空间中我们要求的参数就是决定超平面的 $W$和 $b$ 值。

在超空间中任意一点x到超平面的距离为：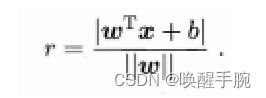

我们可以由特殊到一般的理解一下这个式子，如果在二维空间即平面上，点到直线的距离为：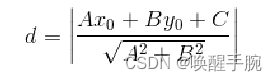

式子中 A，B，C 是直线的参数也就是 W，$x_0$ 和 $y_0$ 是 $x$ 的坐标，这样 $r$ 式是不是就好理解了，这个距离是几何距离，也就是人眼直观看到的距离。

几何距离只有大小没有方向，因为式子是被套上绝对值的，将绝对值摘掉，现在我们就人为规定，样本数据中到超平面的距离为正的点为 +1 类的样本点，就是这类点给它打个标签 +1，到超平面的距离为负的点标签为 -1。

问题：为什么不是 +2，-2 其实都可以，取 1 是为了后续方便计算。

比如现在假设这个超平面能够将样本正确分类，只不过这个超平面的 $w$ 和 $b$ 值我们不知道，这正是我们要求的，但是这个平面是一定存在的，则有如下：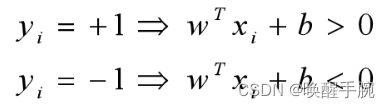

将几何距离r式中的分子绝对值和分母拿掉以后（因为都为正）剩下的 $wT+b$ 是能够判断出样本为 +1 还是 -1 类别的部分，定义函数距离（非常重要）为如下所示：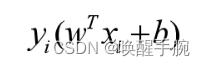

函数距离就是样本类别乘 $wT+b$。因为正样本类别为 +1，且 $wT+b$ 也为正；负样本类别为 -1 且$wT+b$ 为负。所以函数距离只有大小没有方向。

函数距离就相当于几何距离的分子部分，在所有样本中每一个点都有一个函数距离和一个几何距离，几何距离是可观测到的直接的距离。

函数距离具有如下性质：一个点到超平面的函数距离取决于这个超平面的法向量和 b 值，同一个超平面可以有多组 w 和 b 值，但每组值成比例。w 和 b 值不同，点的函数距离也不同。

支持向量机最大间隔（margin）的超平面

重点：支持向量机数学模型原理，其实就是通过控制函数距离来求得最大几何距离。也就是函数距离为约束条件，几何距离为目标函数。具体往下看：

通过放缩 w 和 b，让两类中某一类点距超平面的函数距离分别为1（离超平面的距离相等，为 1 方便后续计算）。

W 和 b 值未知，但总存在一组值满足上述。如图：

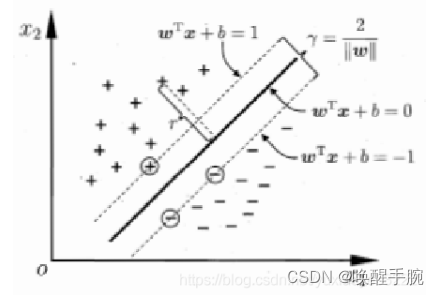
中间最粗的平面为我们要求的超平面，两边的虚线为支撑平面，支撑平面上的点就是支持向量，通过放缩超平面的w和b值，使支持向量到超平面的函数距离为 1，支持向量是距超平面最近的点，所以其他向量点到超平面的函数距离一定大于等于 1。

解释一下这个模型，首先先不看目标函数，先看约束条件，约束添加表达的是所有样本点到超平面的距离要大于等于 1，在支撑平面上的为 1，其他的大于 1，根据约束条件其实可以得到无数个平面，如下面两个所展示：

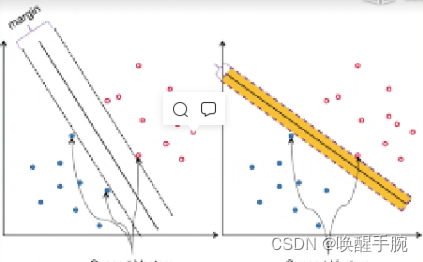
但是，在这些平面中我们需要的是泛华能力最好，鲁棒性最强的那一个，也就是最宽的那一个（margin最大），这时候就需要通过定义目标函数来求得，宽度最大也就是几何距离最大，几何距离的分子是函数距离，而两个支撑平面的函数距离我们定义完了是 2，所以才有了上面的数学模型。

总的来说，就是通过函数距离作为约束条件得到无数个能把样本正确分开的平面，然后通过目标函数在这些平面中找最宽的。把上面的数学模型转化为：

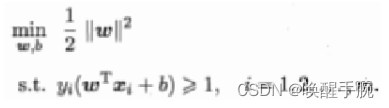
把求最大转变为求最小，即把模型转化为凸函数，其实到这里已经是优化问题了，凸函数是比较容易找到最优解的，因为局部极值就等于全局极值。至于为什么加个二分之一的系数，加个平方，都是为了后续解模型时求导方便。这个模型即为支持向量机的基本型，后面涉及到的软间隔，支持向量回归都从这个形式出发。

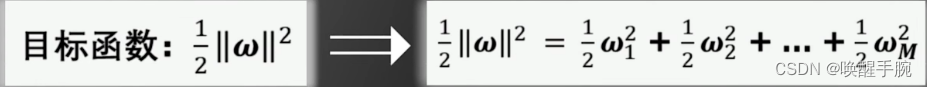
特别注意：凸优化问题，要么无解，要么存在唯一的最优解。

核函数

支持向量机算法分类和回归方法的中都支持线性性和非线性类型的数据类型。非线性类型通常是二维平面不可分，为了使数据可分，需要通过一个函数将原始数据映射到高维空间，从而使得数据在高维空间很容易可分，需要通过一个函数将原始数据映射到高维空间，从而使得数据在高维空间很容易区分，这样就达到数据分类或回归的目的，而实现这一目标的函数称为核函数。