神经网络优化中的学习率调整（上）

神经网络优化中的学习率调整，包括学习率衰减、学习率预热、周期性学习率调整等几种方法

云隐雾匿

2083人浏览 · 2023-03-27 11:58:51

云隐雾匿 · 2023-03-27 11:58:51 发布

学习率是神经网络优化时的重要超参数。在梯度下降法中，学习率 𝛼 的取值非常关键，如果过大就不会收敛，如果过小则收敛速度太慢。常用的学习率调整方法包括学习率衰减、 学习率预热、 周期性学习率调整以及一些自适应调整学习率的方法，比如 AdaGrad、RMSprop、 AdaDelta 等。自适应学习率方法可以针对每个参数设置不同的学习率。

本文主要介绍学习率衰减、学习率预热、周期性学习率调整几种方法 ，在实践中的学习率调整往往几行代码就能实现。

一、学习率衰减

从经验上看，学习率在一开始要保持大些来保证收敛速度，在收敛到最优点附近时要小些以避免来回振荡。比较简单的学习率调整可以通过学习率衰减（Learning Rate Decay ）的方式来实现，也称为学习率退火（ Learning Rate Annealing）。

不失一般性，这里的衰减方式设置为按迭代次数进行衰减。

假设初始化学习率为 𝛼 0 ，在第 𝑡 次迭代时的学习率 𝛼 𝑡。常见的衰减方法有以下几种：

1. 分段常数衰减 （ Piecewise Constant Decay ）：即每经过 𝑇 1 , 𝑇 2 , ⋯ , 𝑇 𝑚 次迭代将学习率衰减为原来的 𝛽 1 , 𝛽 2 , ⋯ , 𝛽 𝑚 倍，其中 𝑇 𝑚 和 𝛽𝑚 < 1 为根据经验设置的超参数。分段常数衰减也称为阶梯衰减（ Step Decay ）。

2. 逆时衰减 （ Inverse Time Decay ）：

其中𝛽 为衰减率。

3. 指数衰减 （ Exponential Decay ）：

其中𝛽 < 1为衰减率。

4. 自然指数衰减 （ Natural Exponential Decay ）：

其中𝛽 为衰减率。

5. 余弦衰减 （ Cosine Decay ）：

其中 𝑇 为总的迭代次数。

下图给出了不同衰减方法的示例（假设初始学习率为1）。

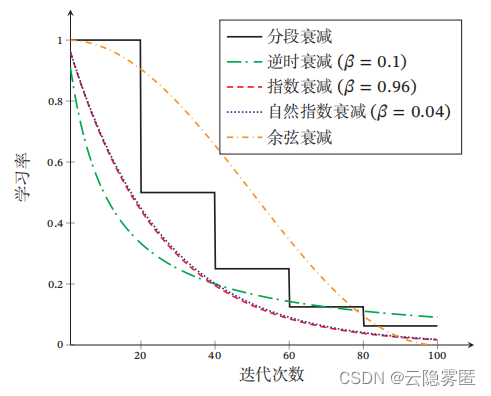
二、学习率预热

在小批量梯度下降法中，当批量大小的设置比较大时，通常需要比较大的学习率。但在刚开始训练时，由于参数是随机初始化的，梯度往往也比较大，再加上比较大的初始学习率，会使得训练不稳定。

为了提高训练稳定性，我们可以在最初几轮迭代时，采用比较小的学习率，等梯度下降到一定程度后再恢复到初始的学习率，这种方法称为 学习率预热 （ Learning Rate Warmup ）。一个常用的学习率预热方法是 逐渐预热 （ Gradual Warmup ）。假设预热的迭代次数为 𝑇 ′ ，初始学习率为 𝛼 0 ，在预热过程中，每次更新的学习率为：

当预热过程结束，再选择一种学习率衰减方法来逐渐降低学习率。

三、周期性学习率调整

为了使得梯度下降法能够逃离鞍点或尖锐最小值，一种经验性的方式是在训练过程中周期性地增大学习率。当参数处于尖锐最小值附近时，增大学习率有助于逃离尖锐最小值；当参数处于平坦最小值附近时，增大学习率依然有可能在该平坦最小值的吸引域（ Basin of Attraction ）内。因此，周期性地增大学习率虽然可能短期内损害优化过程，使得网络收敛的稳定性变差，但从长期来看有助于

找到更好的局部最优解。下文将介绍两种常用的周期性调整学习率的方法： 循环学习率和带热重启的随机梯度下降 。

3.1 循环学习率

一种简单的方法是使用循环学习率（ Cyclic Learning Rate ），即让学习率在一个区间内周期性地增大和缩小。通常可以使用线性缩放来调整学习率，称为三角循环学习率（ Triangular Cyclic Learning Rate ）。

假设每个循环周期的长度相等都为 2Δ𝑇 ，其中前 Δ𝑇 步为学习率线性增大阶段，后Δ𝑇 步为学习率线性缩小阶段。在第 𝑡 次迭代时，其所在的循环周期数 𝑚 为

其中 ⌊⋅⌋ 表示 “ 向下取整 ” 函数。第 𝑡 次迭代的学习率为：

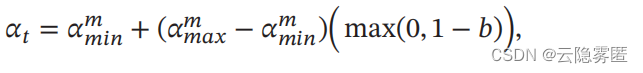
其中 𝛼 ( 𝑚) 𝑚𝑎𝑥 和 𝛼 ( 𝑚) 𝑚𝑖𝑛 分别为第 𝑚 个周期中学习率的上界和下界，可以随着 𝑚 的增大而逐渐降低； 𝑏 ∈ [0, 1] 的计算为:

3.2 带热重启的随机梯度下降

带热重启的随机梯度下降 （ Stochastic Gradient Descent with Warm Restarts， SGDR）是用热重启方式来替代学习率衰减的方法。学习率每间隔一定周期后重新初始化为某个预先设定值，然后逐渐衰减。每次重启后模型参数不是从头开始优化，而是从重启前的参数基础上继续优化。

假设在梯度下降过程中重启 𝑀 次，第 𝑚 次重启在上次重启开始第 𝑇 𝑚 个回合后进行， 𝑇 𝑚 称为重启周期。在第 𝑚 次重启之前，采用余弦衰减来降低学习率。第 𝑡 次迭代的学习率为：

其中 𝛼 ( 𝑚) 𝑚𝑎𝑥 和 𝛼 ( 𝑚) 𝑚𝑖𝑛 分别为第 𝑚 个周期中学习率的上界和下界，可以随着 𝑚 的增大而逐渐降低； 𝑇 𝑐𝑢𝑟 为从上次重启之后的回合（ Epoch ）数。 𝑇 𝑐𝑢𝑟 可以取小数，比如0.1 、 0.2 等，这样可以在一个回合内部进行学习率衰减。重启周期 𝑇 𝑚 可以随着重启次数逐渐增加，比如 𝑇 𝑚 = 𝑇 𝑚−1 × 𝜅 ，其中 𝜅 ≥ 1 为放大因子。

下图给出了两种周期性学习率调整的示例（假设初始学习率为1），每个周期中学习率的上界也逐步衰减。