1、背景

1.1 神经元模型

神经元结构实质上是模拟生物的神经元结构设计的，如下图：

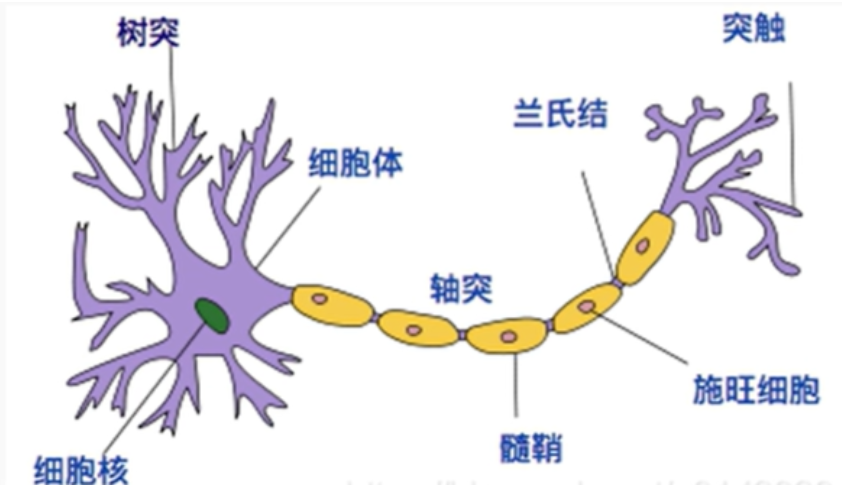
每个节点的值都经过变换后到达下一个节点，如下图，X1到Xn作为输入经过一W1到Wn的变换后到达下一个节点，但是这些值必须经过一个激活函数才可以使用。

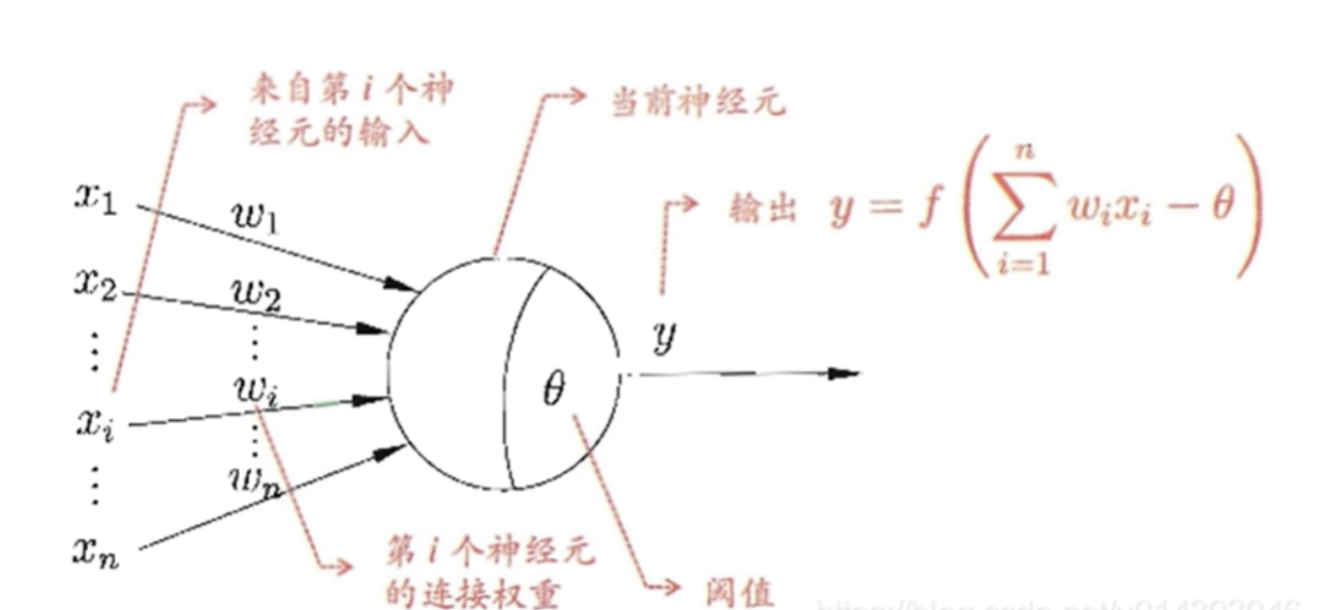
1.2 sigmoid激活函数

主要介绍sigmoid函数，这是一个归一化函数，方便收敛，能够将无穷大的数缩小到0-1之间，方便程序计算，也作为神经元的激活函数。其公式为：

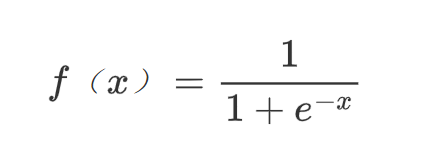
其数学图形为：

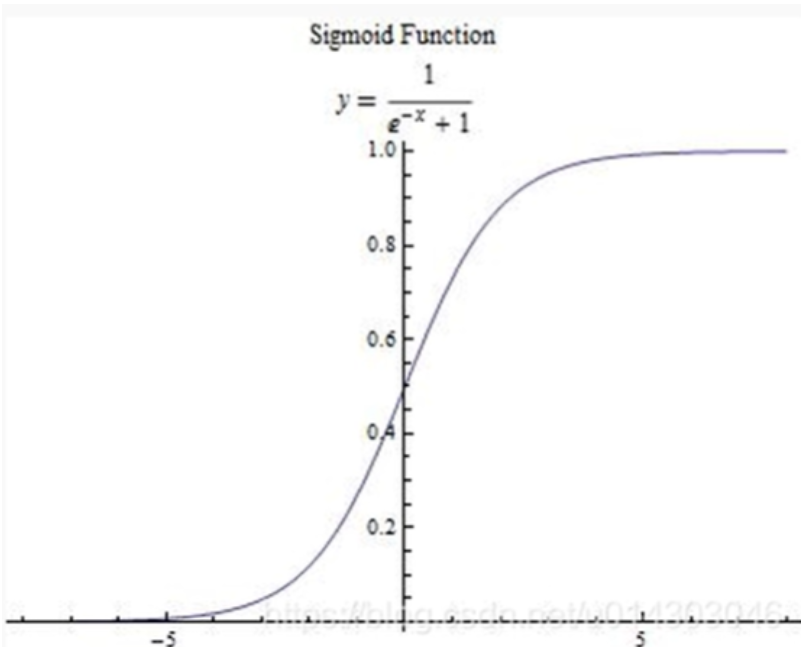
1.3 神经网络结构

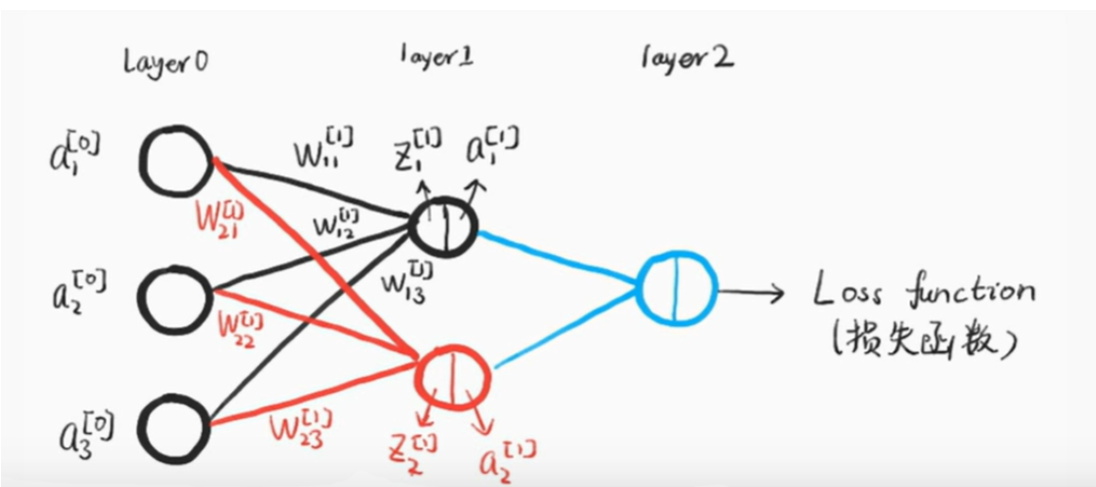
神经网络结构可以分为简单的三级结构输入成、隐藏层（可以有无穷多个）、输出层。如下图第0层是输入层（有三个神经元）、第1层是隐藏层（有两个神经元）、第2层是输出层（有一个神经元）：

1.4 梯度下降算法

梯度下降算法是一种常见优化算法，用于训练神经网络模型。基本思想是通过不断的更新迭代模型参数K、P，使损失函数的值最小化。

神经网络模型中的每个参数都与损失函数相关，梯度下降算法利用损失函数计算K、P参数的梯度，然后按照梯度的反方向调整参数的值，使误差最小化。其简易步骤如下：

• 初始化模型参数：随机初始化参数的权重和偏置。

• 前向传播：利用当前模型的参数计算输出。

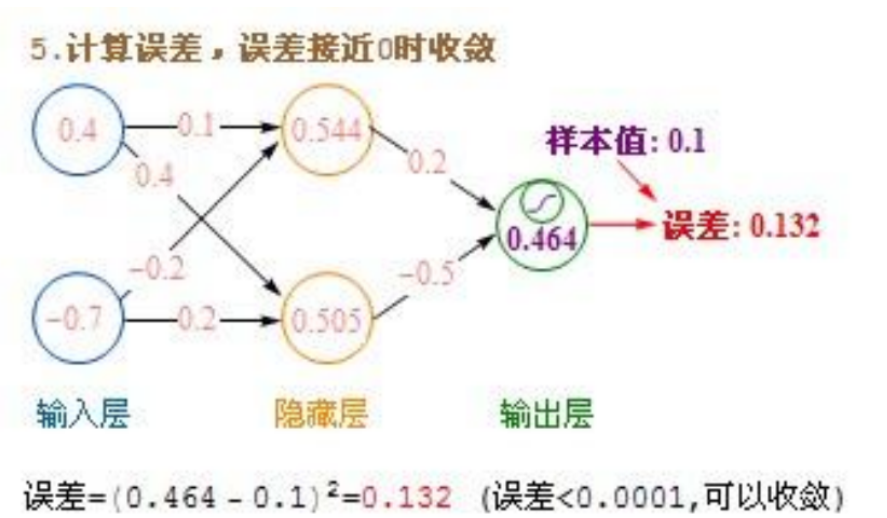
• 计算损失函数：将模型输出与实际值作比较，计算损失函数。

• 反向传播：利用损失函数计算K、P参数的梯度。反向传播利用链式法则将梯度由输出传到输入层。

• 更新参数的值：按照梯度的反方向更新K、P参数的值。

• 迭代：一直重复前向传播、计算损失函数、反向传播、更新参数的几个步骤，直到超出迭代条件。

1.5 BP算法（误差反向传播算法）的由来

梯度下降算法需要不断更新K、P两个参数的值，使误差达到最小化。实际上神经网络模型中不止，网络中的每条连接都有权重参数，怎样调整这些参数可以使误差最小化，引入了误差反向传播算法：BP算法。

2、BP算法基本原理以及公式推导

2.1 BP算法基本原理

BP算法是一种有效计算偏导的方法，它的基本原理是利用前向传播的输出结果对误差进行求偏导，然后将偏导数传入隐藏层进行加权求和，这样一层一层的向前传，直到传到输入层（输入层不参与计算），最后利用各个节点的偏导数进行权重更新。

2.2 BP神经网络整体框架

BP算法的整体框架如下图。前向传播过程中利用随机的初始化参数以及权重计算模型的输出。反向传播过程中利用输出与理想的标签值作比较计算出损失函数，并利用损失函数计算参数w、b的梯度，然后按照梯度反向调整w、b的值。测试模型过程中，利用搭建好的模型对进行训练，查看误差值。：

2.3 BP神经网络的公式推导

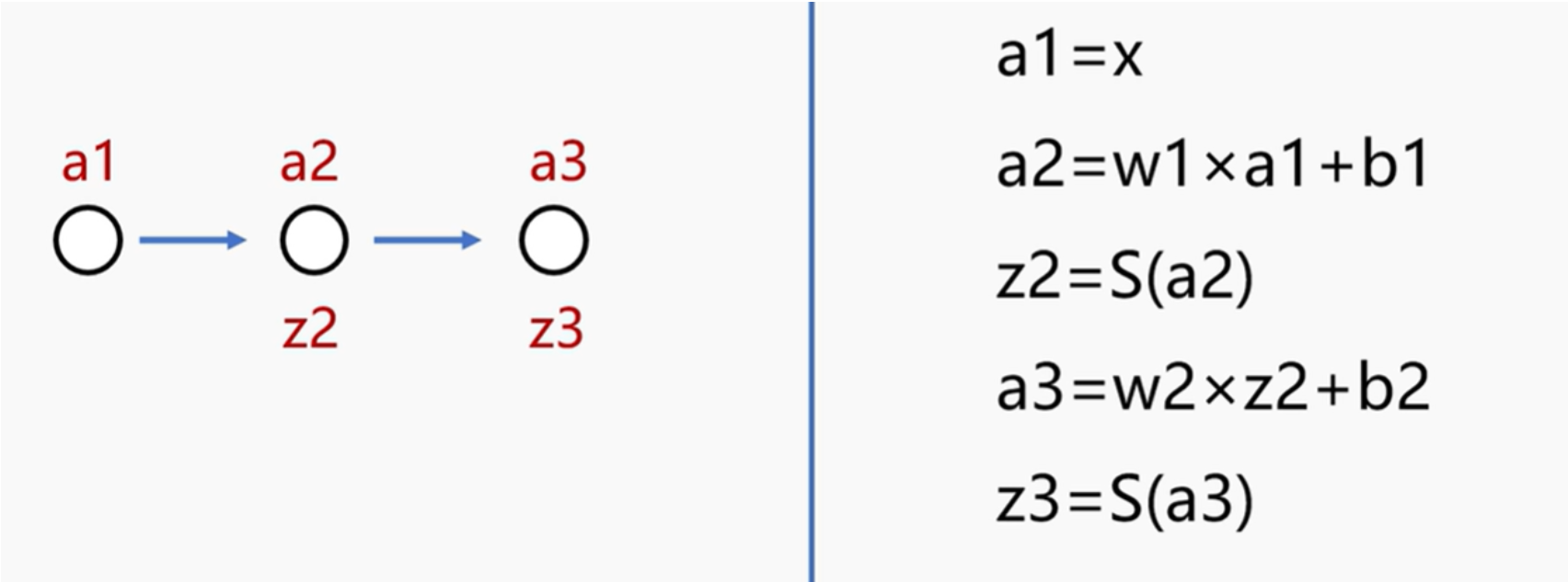
前向传播可以细致为下图。a1为输入的初始参数，经过w1变换和b1梯度调整后得到a2，a2又通过sigmoid激活函数得到z2，z2经过w2变换和b2梯度调整后得到a3，a3又通过sigmoid激活函数得到z3.

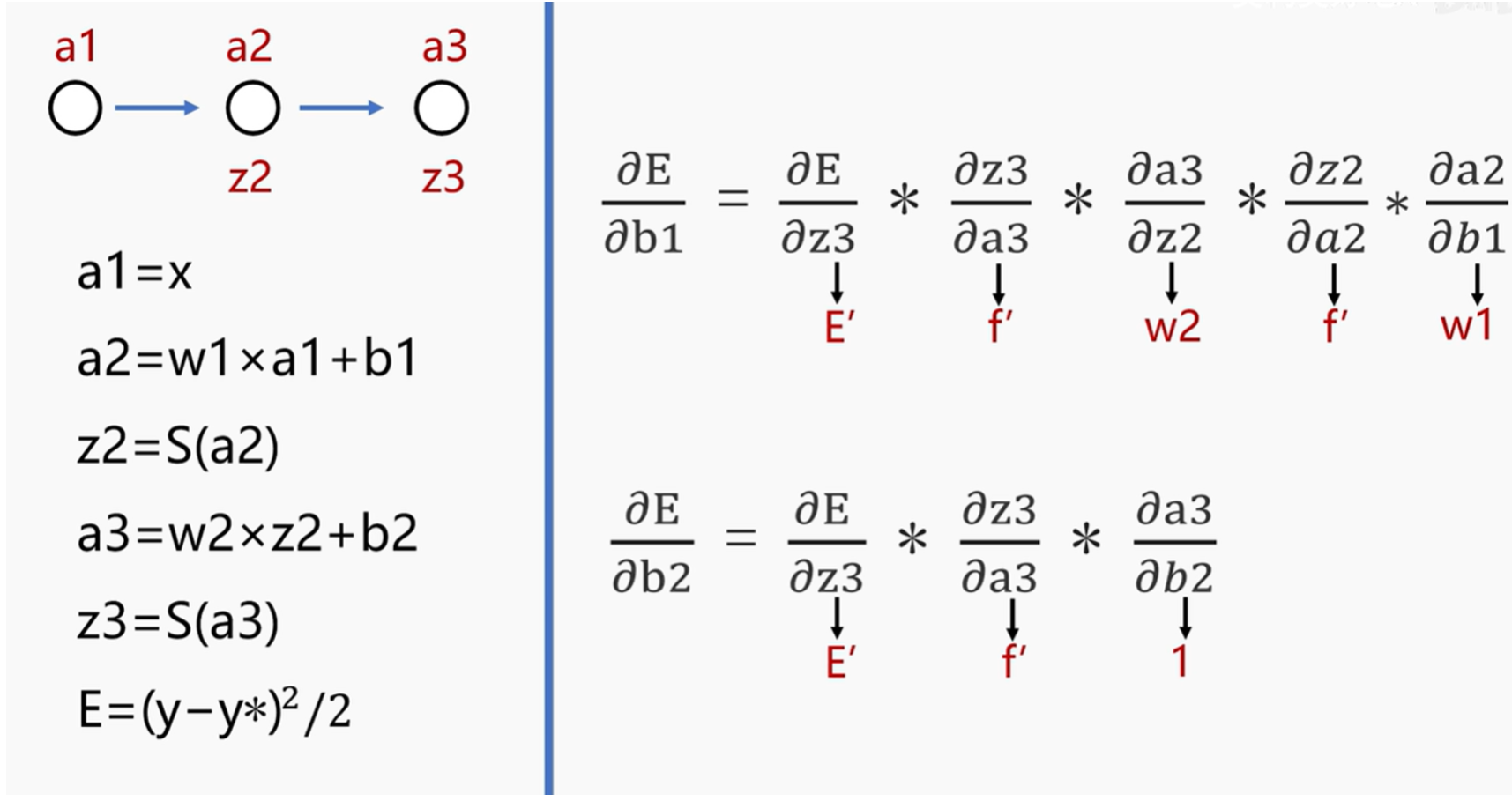
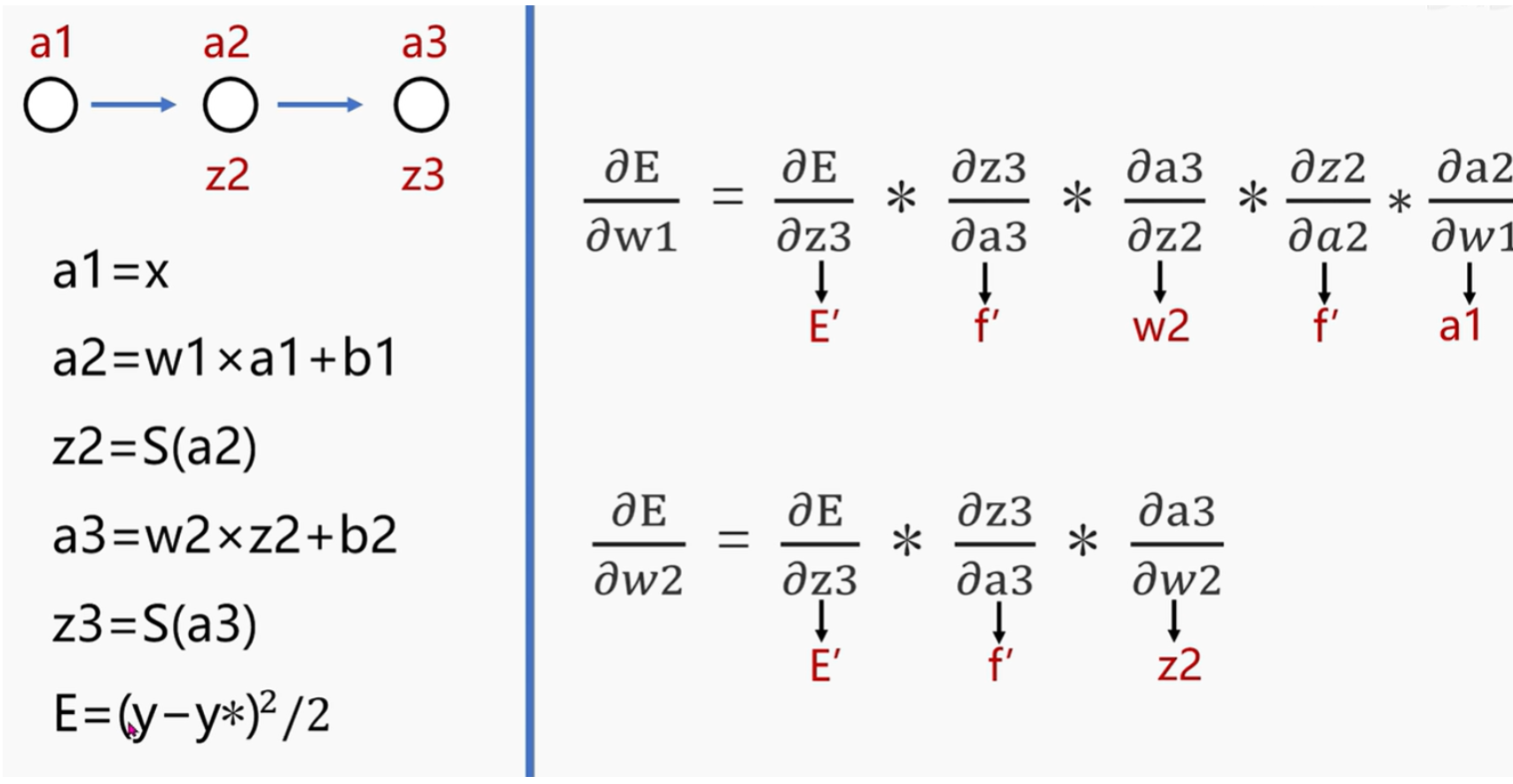
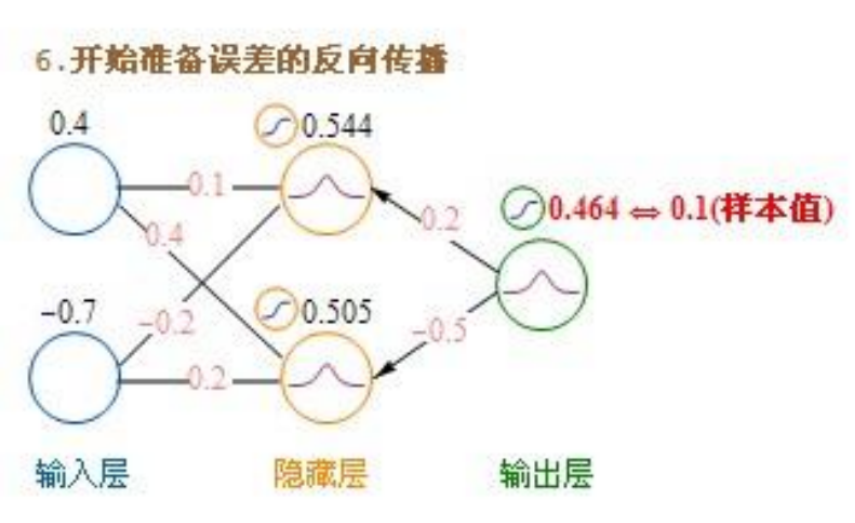
误差反向传播是利用梯度下降的方法，由输出值的差值求出误差，使误差沿着w、b的反向减小。如下图，E就是需要求取的误差，利用E对w、b两个参数求偏导，其中f’是指对于sigmoid函数求导，红色字体是每个对应偏导的结果。

3、sigmoid激活函数残差（误差的导数）的计算公式、权重增加的计算公式

3.1 残差计算公式

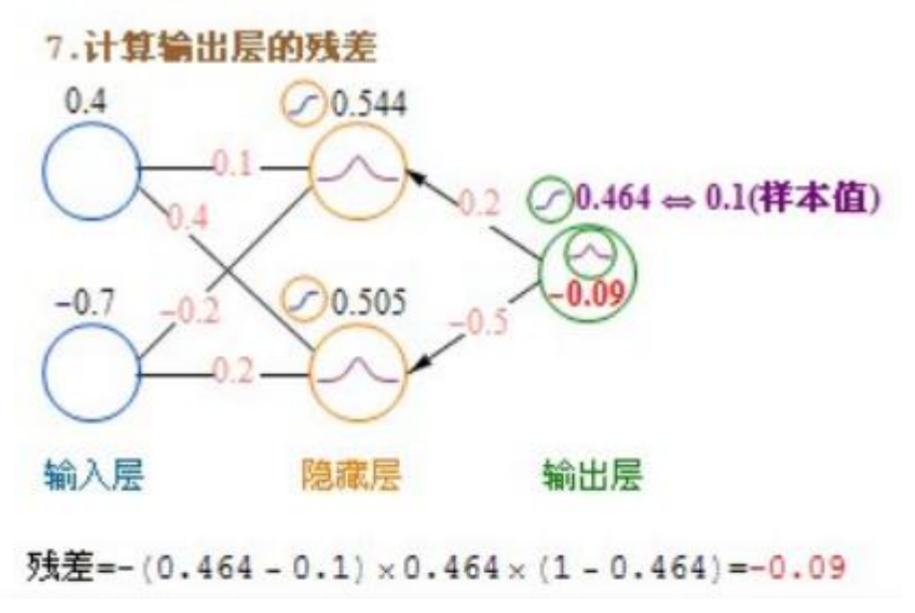
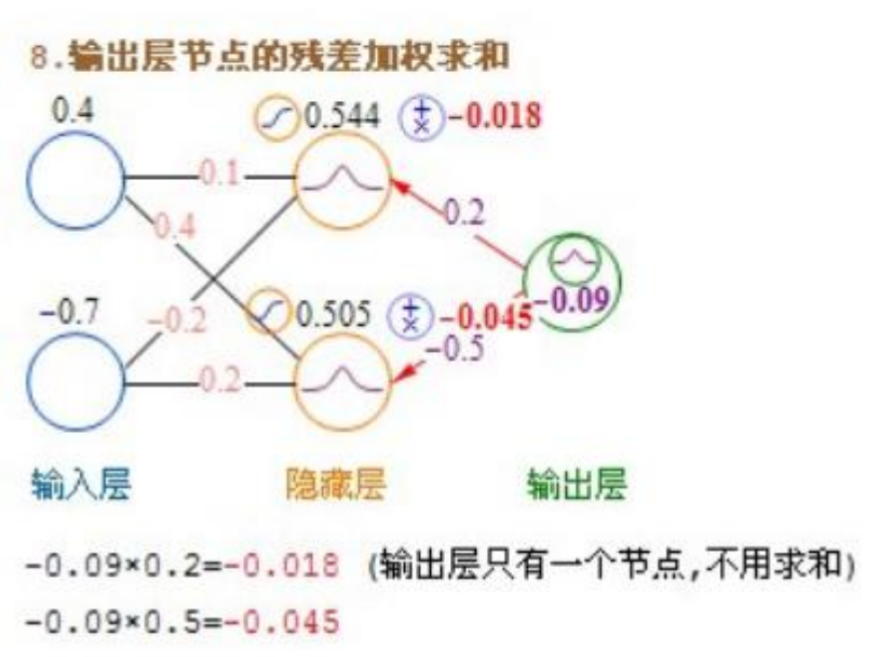
输出层→隐藏层的残差计算公式：-（输出值-样本值)*激活函数导数

隐藏层→隐藏层残差计算公式：（右侧每个节点残差加权求和）*激活函数导数

3.2 sigmoid激活函数残差计算公式

输出层→隐藏层的sigmoid残差计算公式：-（sigmoid输出值-样本值）* sigmoid * （1-sigmoid）=-（输出值-样本值）* 输出值 *（1-输出值）

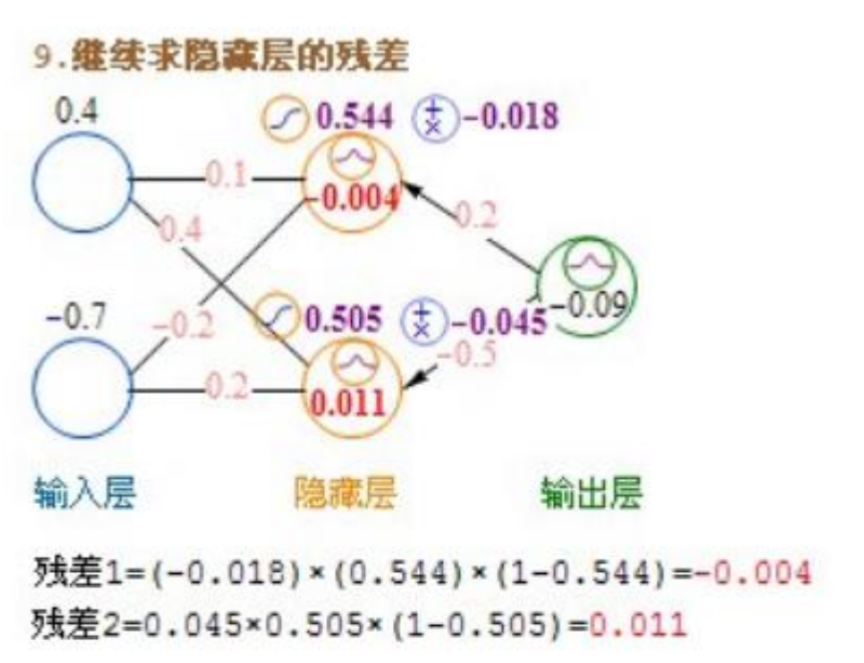
隐藏层→隐藏层的sigmoid残差计算公式：（右侧每个节点的残差加权求和）* 当前节点的sigmoid值 * （1-当前节点的sigmoid值）

3.3 权重增加公式

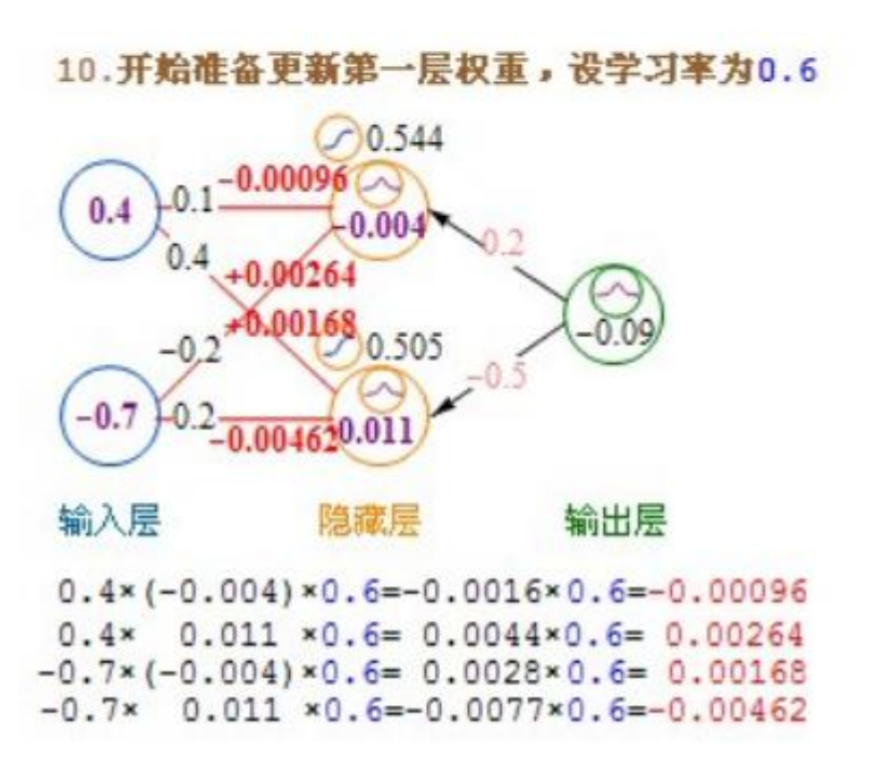
输入层权重增加公式：当前节点sigmoid值 * 右侧对应节点残差 * 学习率

隐藏层权重增加公式：输入值 * 右侧对应节点残差 * 学习率

偏移值的权重增加公式：右侧对应节点残差 * 学习率

---

注意：

• 学习率是指提前设置好的参数，用于控制每次更新的幅度。

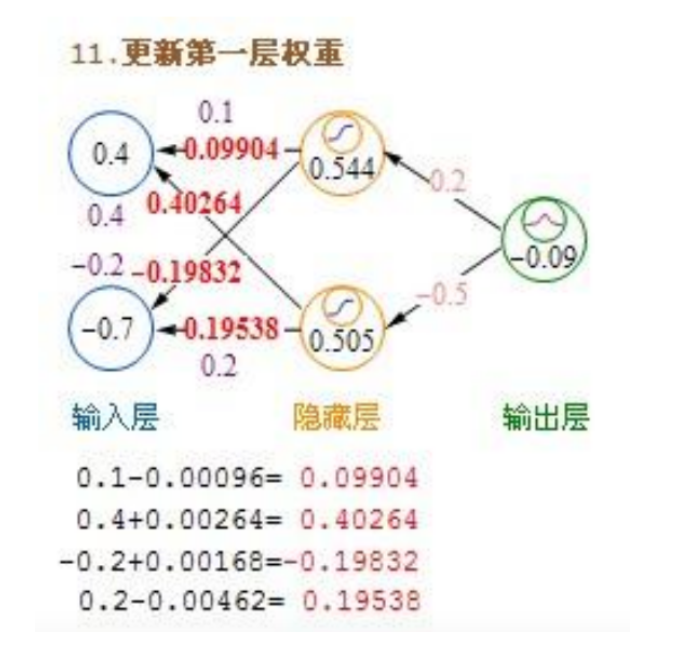
• 这里计算的是增加的权重，最终权重是值原始权重加上增加权重。

4、BP算法实例

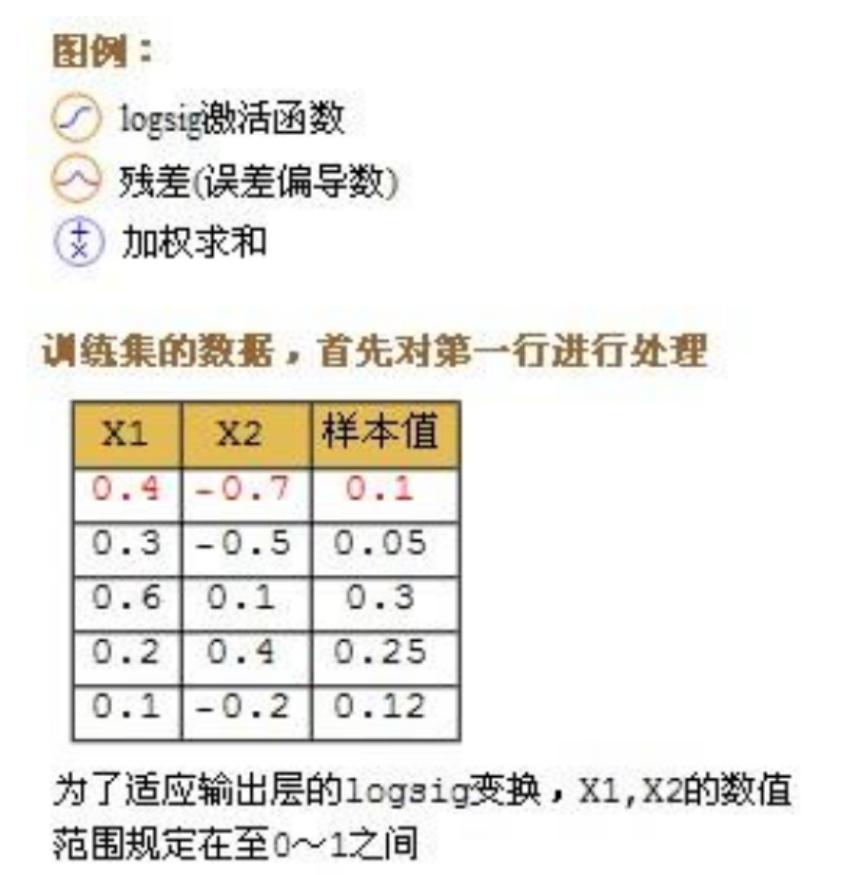
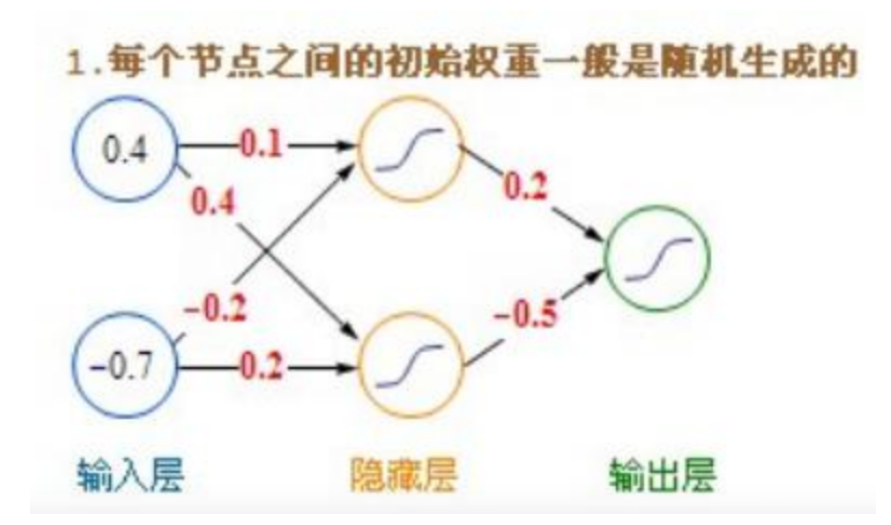
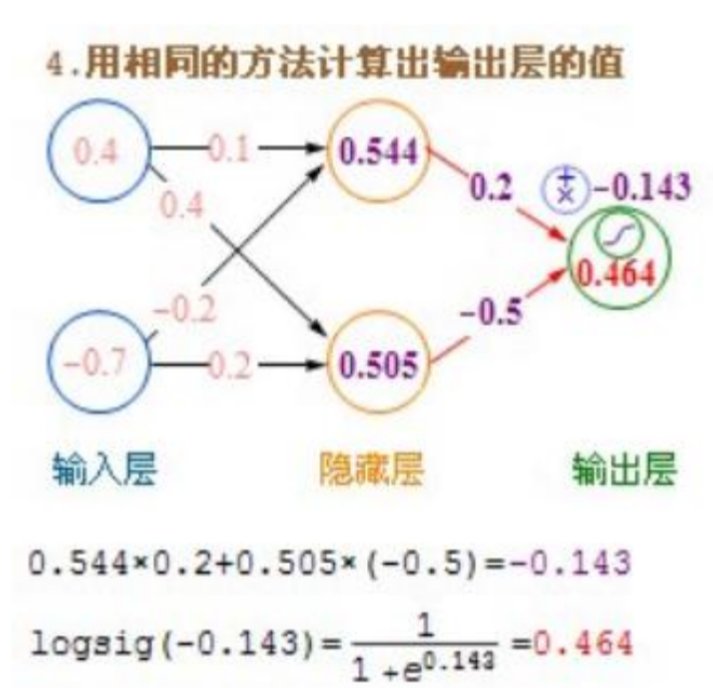
如上图中的红色字体就是权重值，也就是我们在2.3节当中讲到的w、b参数。

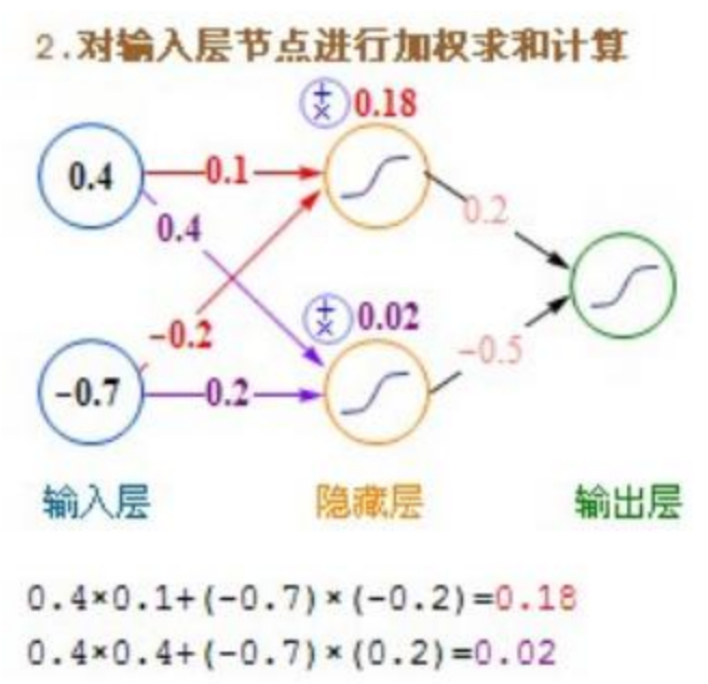
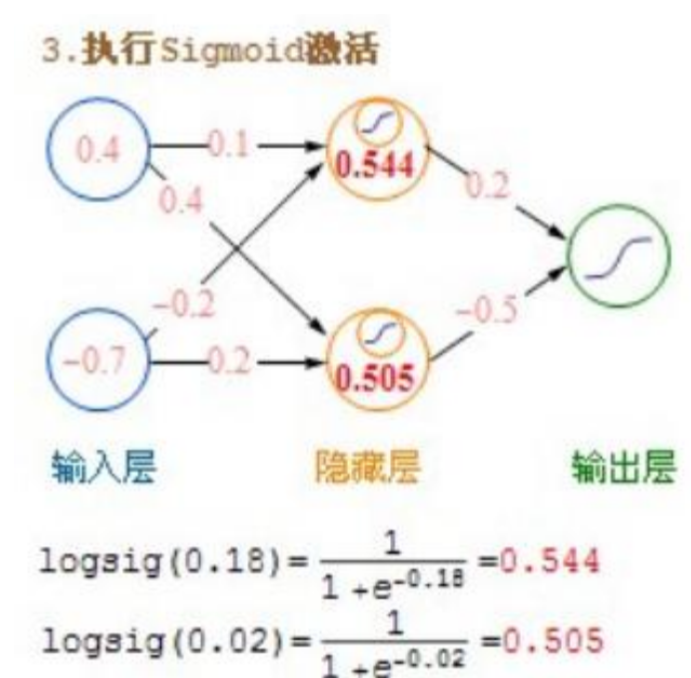
如上图就像2.3节所讲的，每个节点的值不仅仅是前一个节点的加权求和，还要使用激活函数。

5、BP神经网络的特点与局限

BP神经网络的特点和局限性可以分为以下几点：

• BP神经网络可以进行分类、聚类、预测，需要大量的历史数据，通过对历史数据的训练，网络会找出数据中一些隐藏的知识。

• BP神经网络是根据实践建立起来的系统，并不是仿生系统，实用性非常好。

• BP神经网络系统中，像隐藏层节点数量如何获得、如何初始化参数、使用何种激活函数等等问题都是没有理论支撑的，而是通过大量的实践经验获得的。

• BP神经网络是有效的计算方法，但是它的计算复杂度大、计算时间周期长、容易陷入局部最优化等局限性也是广为人知的。