第3.1章 卷积神经网络CNN-基础概念
一、背景
二、引入卷积神经网络的原因
三、“卷积”的概念
四、基本的卷积操作的改进
   1.padding
   2.stride
五、卷积网络中三种类型的层
   1.Convolution(CONV)
   2.Pooling(POOL)
   3.Fully Connected(FC)
六、一个简单的CNN的结构图
一、背景
   在机器学习大热的前景之下，计算机视觉(Computer Vision)、自然语言处理(Natural Language Process,NLP)、语音识别(Speech Recognition)并列为机器学习方向的三大热点方向。
   计算机视觉(Computer Vision)包括：图像分类(Image Classification)、目标检测(Object Detection)、风格迁移(Neural Style Transfer)、语义分割(Semantic Segmentation)等。

二、引入卷积神经网络的原因
   在计算机视觉领域，需要处理大量图像数据。假设一张小图像包含的数据量为1000×1000×3(rgb，3通道)，如果把这些数据直接作为神经网络的输入层，将会导致输入层单元非常多，从而导致计算量非常大（假设隐藏层单元有1000个，则输入层和第二层之间的权重向量的大小为3,000,000×1000）。有这么多的参数，我们很难获得足够的数据以避免神经网络过拟合；同时，训练一个有这么多参数的神经网络，对计算量和内存的需求相当大。所以为了能在计算机视觉中尽情地使用任意大小图像，基于卷积运算的卷积神经网络(Convelutional Neural Network)出现了。

   CNN是如何减少参数的呢？
   先简单解释一下。相比于把整个图像所含的数据直接作为输入层数据的方法，CNN中的参数只有卷积核中的参数，还可以算上偏置(bias)这一个参数。就算我们把卷积核的大小设定为原始图像的大小(1000×1000×3)，参数数目也是少于全连接网络的(3,000,000×1000)。当然我们不会设的那么大，所以CNN的参数数目确实是大大减少了。

三、“卷积”的概念
   “卷积”是卷积神经网络的核心，关于卷积神经网络中卷积的运算方法参见深入学习卷积神经网络（CNN）的原理知识中的“3.4 卷积(convolution)”

   我们通过上图解释一下几个概念：上图中一个3×3的小单元格叫做一个过滤器(filter)；每一行代表一个卷积运算过程，即一个卷积层。
   1）过滤器的种类
   CNN中有好多不同种类的过滤器，如Sobel过滤器、Scharr过滤器等。我们可以通过选用不同种类的过滤器来指定过滤器的值，也可以用CNN来习得过滤器中的值。

 
   2）过滤器的大小
   过滤器的大小是不确定的，可以是3×3、5×5、7×7等，但大多都是奇数。原因之一是奇数大小的过滤器有一个中心位置(可以称之为中心像素)，这样就可以描述过滤器的位置。还有一个原因和计算output layer的大小有关。当然，如果使用偶数大小的过滤器也没有关系，不过大家都习惯用奇数的而已。

卷积神经网络张量(图像)的尺寸和参数的计算

如何计算张量（图像）的尺寸
如何计算网络的总参数
   3）过滤器中值的意义
   如下图所示，请注意用红色圆圈圈起来的部分。原始图像通过过滤器，将过滤器希望提取的特征提取出来了。
   首先需要知道，图中“1”表示白色亮度，“-1”表示黑色亮度，介于两者之间数值的亮度递减。比如第一个，过滤器的主对角线是1，最后得到的图像，显然在主对角线上的亮度明显高于其他地方。

   读完上面，我们再来解释一下CNN是如何减少参数的：

参数共享
   相比全连接网络一个参数对应一个数据特征，卷积网络中过滤器与特征之间不是一一对应的，实现了参数共享。
稀疏连接（感受野。对比全连接理解）
   原始图像与过滤器进行卷积运算后得到的那一个值，只与原始图像上参与运算的那一个矩形区域有关，和其他部分无关。
四、基本的卷积操作的改进
   1.padding
使用padding的原因：
   1）由上图可以看到，每经过一次过滤，图像就会变小。
   2）对于原始图像四个顶点部分的数据，只会被一个过滤器使用，导致边缘信息丢失。
  因此，在卷积操作之前，先在原始图像边缘进行像素填充，像素值可以是0也可以是图像边缘像素，填充宽度为p，p的值大于等于1即可。如下图，灰色部分是填充部分：

填充多少合适？ 两个常见的选择：valid卷积和same卷积
  same卷积：选择的填充将使得输出大小等于输入大小
  valid卷积：不填充
   2.stride
  卷积上下左右移动的步长，如下图。上面是步长为1，下面是步长为2。

3.stripe作用

4. tile基本概念

5. 每个tile输入的FM向量

6. 在常规3d卷积运算中,假设卷积层中输入特征图(feature map)张量形状表示为x[n hi wi ci],卷积核(kernel)的张量形状表示为k[co kh kw ci],输出的结果为y[n h...

问题描述不够清晰，无法直接提供代码解决方案。"每个tile输入的FM向量"这句话可能指的是在一个大数据处理任务中，需要对数据集进行分片（tile）处理，并且每个分片需要计算一个特征向量（Feature Vector）或者特征矩阵（Feature Matrix）。这个特征向量或矩阵通常由一些输入的特征经过某种函数（如FM模型中的Factorization Machine）转换得到。

如果你需要实现这样的功能，可以使用Python的pandas库来进行数据的分片处理，并用scikit-learn库中的FeatureUnion来组合不同的转换方法（包括Factorization Machine）。以下是一个简单的示例，使用了scikit-learn中的DummyFeatureTransformer来代替FM模型，但是原理是一样的。

五、卷积网络中三种类型的层
   1.Convolution(CONV)
   之前介绍的进行卷积操作的一个过程就是一个卷积层。

   2.Pooling(POOL)
作用
   Andrew Ng 对池化层的作用是这样解释的：“ConvNets often also use pooling layers to reduce the size of the representation, to speed the computation, as well as make some of the features that detects a bit more robust”。即减小图像大小、加速计算、使其检测出的特征更加健壮。
参数
   没有参数(parameters)需要学习！但是有超参数(hyperparameters)：过滤器大小(f)和步长(s)，一般取f=2,s=2。
种类：Max Pooling、Average Pooling
运算方法：参见深入学习卷积神经网络（CNN）的原理知识中的“3.5 池化(Pooling)”
   3.Fully Connected(FC)
  把最后得到的池化层中的所有参数全部排列成一个列向量，形成全连接层，用于进行分类。

六、一个简单的CNN的结构图

其中，卷积层、池化层作为一个整体可以循环有多层，全连接层可可以有多层。

来源：coursera----Andrew Ng----Converlutional Neural Networks
————————————————

                            版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
                        
原文链接：https://blog.csdn.net/dear_jing/article/details/102786588

1.3.1.1. 神经网络处理

对于神经网络中的每一层，输入数据都必须转换为输出数据。一种经常使用的变换是卷积，它将输入数据与一组训练好的权重进行卷积，或者更准确地说，进行相关。这种变换用于卷积神经网络(CNN)，而卷积神经网络通常应用于图像或视频识别。

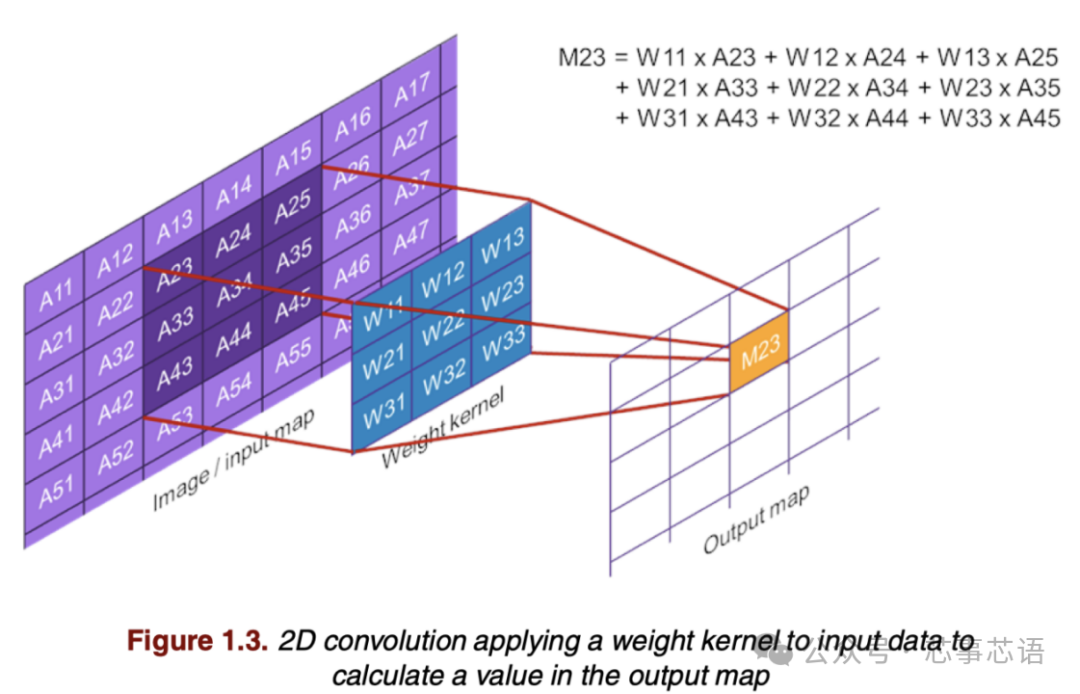
图1.3 显示了 2D 卷积，它使用 2D 权重核的权重和输入数据中与权重核具有相同宽度和高度的选定 2D 区域执行点积运算。点积在输出图中产生一个值 (M23)。在此示例中，输入数据的边界未应用任何填充，因此输出值的坐标为 (2, 3)。为了计算完整的输出图，权重核在输入图上“移动”，并对选定的 2D 区域执行点积运算，每个点积产生一个输出值。例如，可以通过向右移动一步并对输入样本 A24–A26、A34–A36 和 A44–A46 的区域执行点积来计算 M24。

输入和输出图通常是三维的。也就是说，它们具有宽度、高度和深度，深度维度上的不同平面通常称为通道。对于深度> 1 的输入图，可以使用来自多个输入通道的输入数据上的点积运算来计算输出值。对于深度 > 1 的输出图，必须对每个输出通道执行卷积，对不同的输出通道使用不同的权重核。深度卷积是一种特殊的卷积层类型，其输入和输出通道的数量相同，每个输出通道都从与输出通道具有相同深度值的一个输入通道计算得出。另一种层类型是全连接层，它使用与输入图中的样本数量相同的权重对每个输出值执行点积运算。

上述层类型中的关键操作是对输入样本和权重的点积运算。因此，处理器需要有效地实现此类点积运算。这涉及高效计算，例如使用MAC 指令，以及高效访问输入数据、权重核和输出数据。

CNN是前馈神经网络。当某一层处理输入图时，它不会维持任何影响下一个输入图处理的状态。循环神经网络 (RNN) 是一种不同的神经网络，它在处理输入序列时维持状态。因此，RNN 还能够识别跨时间的模式，并且经常应用于文本和语音识别应用。

有许多不同类型的RNN 单元可用于构建网络。在其基本形式中，RNN 单元计算输出，如公式 [1.1] 所示： 

其中xt 是输入序列中的第 t 帧，ht 是 xt 的输出，W x 和 W h 是权重集，b 是偏差，f() 是输出激活函数。因此，输出的计算涉及一组权重与新输入数据的点积，以及另一组权重与先前输出数据的点积。因此，对于 RNN 来说，点积也是必须有效实现的关键操作。长短期记忆 (LSTM) 单元是另一个众所周知的 RNN 单元。LSTM 单元的结构比我们上面讨论的基本 RNN 单元更复杂，但点积再次成为主要操作。

激活函数用于神经网络中，通过执行一些非线性映射来转换数据。例子有整流线性单元(ReLU)、S 型和双曲正切 (TanH)。激活函数对单个数据值进行操作并产生单个结果。因此，对于激活层，输出图的大小等于输入图的大小。

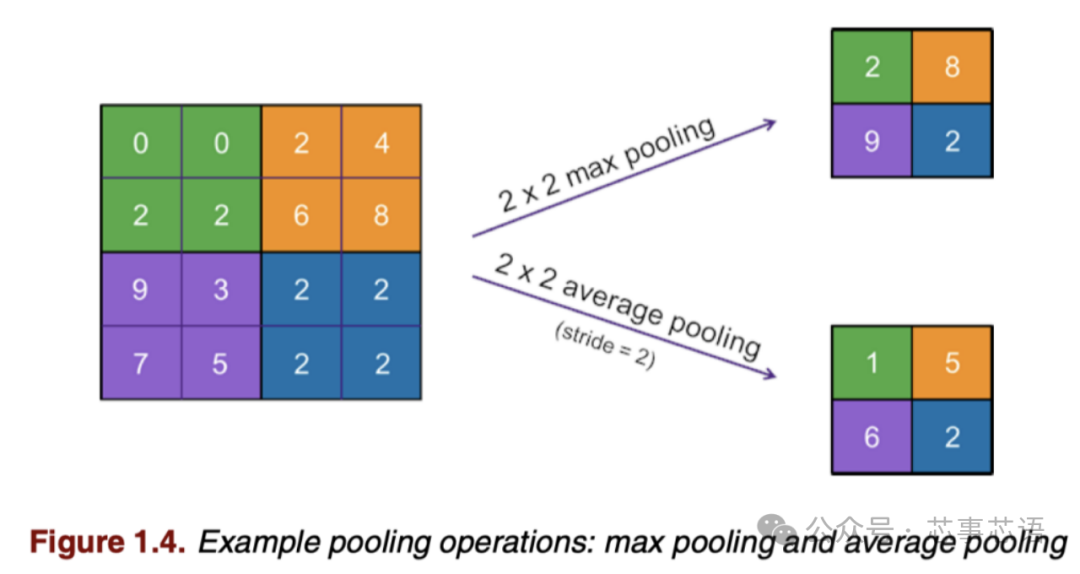
神经网络也可能具有池化层，通过计算输入数据（小）区域的单个输出值，将输入图转换为较小的输出图。图1.4 显示了两个示例：最大池化和平均池化。实际上，池化层在宽度和高度维度上对数据进行下采样。输出图的深度与输入图的深度相同。