1 前言

DCN是一个常见的技术，在Deformable-DETR跟PP-YOLO中都有用到DCN；
论文：《Deformable ConvNets v2: More Deformable, Better Results》

致谢：

感谢Buf哥的文章讲解——《再思考可变形卷积》

2 DCN的特点

• 理论上可以获得任意大小的感受野（由于其deformable的特性）

3 南溪对于DCN的理解

3.1 Modulation mechanism——实现了spatial-attention

在南溪看来，modulation-mechanism实际上实现了一种spatial-attention的操作，对不同的像素值有着不同的权重；

3.2 Deformable——具有变形能力的稀疏采样

DCN通过其deformable的能力实现了一种learnable的稀疏采样，在固定参数量的情况下，使得卷积核具有变形采样的能力；
从神经元的连接性上来说，DCN实现了一种固定数量的全局连接，通过deformable能力实现与上层特征图任意位置的连接，体现了神经元连接的复杂特性；

4 DCN的使用——“在哪里加入DCNv2?”

这里我们参考了飞桨的DCN实现，以下是PyTorch格式的配置：
dcn_v2_stages: [2, 3, 4]
结论：
我试过resnet50_dcn的效果很好，以下是实验结果的截图，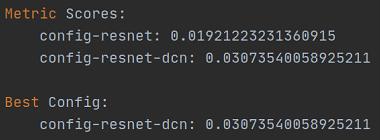

5 DCNv2的实现——基于PyTorch实现

参考GitHub项目——4uiiurz1/pytorch-deform-conv-v2

5.1 DeformConv2d [source]

DCNv2模块的nn.Module类；
当前版本的代码实现仅支持3x3卷积；

• inc：表示输入通道数；
• outc：表示输出通道数；
• kernel_size：表示卷积核的大小；

5.1.1 类的构造__init__()函数

# inc表示输入通道数
# outc 表示输出通道数
# kernel_size表示卷积核尺寸
# stride 卷积核滑动步长
# bias 偏置
# modulation DCNV1还是DCNV2的开关
def __init__(self, inc, outc, kernel_size=3, padding=1, stride=1, bias=None, modulation=False):
    """
    Args:
        modulation (bool, optional): If True, Modulated Defomable Convolution (Deformable ConvNets v2).
    """
    super(DeformConv2d, self).__init__()
    self.kernel_size = kernel_size
    self.padding = padding
    self.stride = stride
    self.zero_padding = nn.ZeroPad2d(padding)
    # 普通的卷积层，即获得了偏移量之后的特征图再接一个普通卷积
    self.conv = nn.Conv2d(inc, outc, kernel_size=kernel_size, stride=kernel_size, bias=bias)
    # 获得偏移量，卷积核的通道数应该为2*ks*ks
    # padding = (ks-1)//2, 当ks=3时，padding=1
    self.p_conv = nn.Conv2d(inc, 2*kernel_size*kernel_size, kernel_size=3, padding=1, stride=stride)
    # 偏移量初始化为0，（即开始是标准的正方形卷积）
    nn.init.constant_(self.p_conv.weight, 0)
    # 注册module反向传播的hook函数, 可以查看当前层参数的梯度
    self.p_conv.register_backward_hook(self._set_lr)
    # 将modulation赋值给当前类
    self.modulation = modulation
    if modulation:
        # 如果是DCN V2，还多了一个权重参数，用m_conv来表示
        self.m_conv = nn.Conv2d(inc, kernel_size*kernel_size, kernel_size=3, padding=1, stride=stride)
        # 初始值设置为0，即：sigmoid(0)=0.5，初始权重为0.5
        nn.init.constant_(self.m_conv.weight, 0)
        # 注册module反向传播的hook函数, 可以查看当前层参数的梯度
        self.m_conv.register_backward_hook(self._set_lr)

# 静态方法 类或实例均可调用，这函数的结合hook可以输出你想要的Variable的梯度
@staticmethod
def _set_lr(module, grad_input, grad_output):
    grad_input = (grad_input[i] * 0.1 for i in range(len(grad_input)))
    grad_output = (grad_output[i] * 0.1 for i in range(len(grad_output)))

5.1.2 _get_p()——获得变形坐标

这个函数用来获取偏移之后相对于原始特征图x的坐标（float）。

• offset：表示偏移坐标；
• dtype：数据类型。

def _get_p(self, offset, dtype):
  	# N = 18 / 2 = 9，表示卷积核的参数数量
    # h = 32
    # w = 32
    N, h, w = offset.size(1)//2, offset.size(2), offset.size(3)

    # (1, 2N, 1, 1)，获得N个卷积点的偏移
    p_n = self._get_p_n(N, dtype)
    # (1, 2N, h, w)，获得每个像素点的坐标
    p_0 = self._get_p_0(h, w, N, dtype)
    # 卷积坐标加上之前学习出的offset后就是论文提出的公式(2)也就是加上了偏置后的卷积操作。
    # 比如p(在N=0时)p_0就是中心坐标，而p_n=(-1,-1)，所以此时的p就是卷积核中心坐标加上
    # (-1,-1)(即红色块左上方的块)再加上offset。同理可得N=1,N=2...分别代表了一个卷积核
    # 上各个元素。
    p = p_0 + p_n + offset
    # 在进行offset的加法时，会产生广播操作，最终的结果p--[B, H, W, 2N]
    return p

5.1.3 _get_x_q()——取值函数

通过索引获得张量中指定位置的值；
关于这个函数，南溪之前困惑了很久，不知道为什么要用一个padded_w ，这里出现padded_w 的主要原因是在forward()函数中有对x进行padding，即：

if self.padding:
   x = self.zero_padding(x)
   # self.zero_padding实际上就是nn.ZeroPad2d()函数

这里南溪当时一直不是很理解这里为什么要进行padding，后来想了一下终于明白了，因为在进行卷积时，其实真正参与运算的不是x，而是经过padding之后的潜在张量x_la，所以通过p_conv获得的偏移实际上是潜在特征图x_la的坐标偏移，而不再是x的坐标偏移了，所以在使用_get_x_q取值前，首先需要获得潜在特征图x_la；

• x：需要获取的张量；
• q：[b, h, w, 2N]，表示像素点的索引。

def _get_x_q(self, x, q, N):
    b, h, w, _ = q.size()
    # 获得x_la的宽度
    padded_w = x.size(3)
    c = x.size(1)
    # (b, c, h*w)
    x = x.contiguous().view(b, c, -1)

    # (b, h, w, N)
    index = q[..., :N]*padded_w + q[..., N:]  # offset_x*w + offset_y
    # (b, c, h*w*N)
    index = index.contiguous().unsqueeze(dim=1).expand(-1, c, -1, -1, -1).contiguous().view(b, c, -1)

    x_offset = x.gather(dim=-1, index=index).contiguous().view(b, c, h, w, N)

    return x_offset

5.1.2 forward()——前向传播函数

# 前向传播函数
def forward(self, x):
    # 获得输入特征图x的偏移量
    # 假设输入特征图shape是[1,3,32,32]，然后卷积核是3x3，
    # 输出通道数为32，那么offset的shape是[1,2*3*3,32]
    offset = self.p_conv(x)
    # 如果是DCNv2那么还需要获得输入特征图x偏移特征图的权重项
    # 假设输入特征图shape是[1,3,32,32]，然后卷积核是3x3，
    # 输出通道数为32，那么offset的权重shape是[1,3*3,32]
    if self.modulation:
        m = torch.sigmoid(self.m_conv(x))
        # 这个sigmoid用的很酷，可以增加非线性
    # dtype = torch.float32
    dtype = offset.data.type()
    # 卷积核尺寸大小
    ks = self.kernel_size
    # N=2*3*3/2=3*3=9
    N = offset.size(1) // 2
    # 如果需要Padding就先Padding
    if self.padding:
        x = self.zero_padding(x)
        # self.zero_padding实际上就是nn.ZeroPad2d()函数

    # p的shape为[1, 2N, H, W]
    # 这个函数用来获取所有的卷积核偏移之后相对于原始特征图x的坐标（现在是浮点数）
    p = self._get_p(offset, dtype)

    # 我们学习出的量是float类型的，而像素坐标都是整数类型的，
    # 所以我们还要用双线性插值的方法去推算相应的值
    # 维度转换，现在p的维度为[B, 2N, H, W]
    p = p.contiguous().permute(0, 2, 3, 1)
    # 转换之后为[B, H, W, 2N]
    # l:left, r:right; t:top, b:bottom
    # floor是向下取整
    q_lt = p.detach().floor()
    # +1相当于原始坐标向上取整
    q_rb = q_lt + 1
    # 将q_lt即左上角坐标的值限制在图像范围内，torch.clamp用来限定张量值的范围
    q_lt = torch.cat([torch.clamp(q_lt[..., :N], 0, x.size(2)-1), torch.clamp(q_lt[..., N:], 0, x.size(3)-1)], dim=-1).long()
    # 将q_rb即右下角坐标的值限制在图像范围内
    q_rb = torch.cat([torch.clamp(q_rb[..., :N], 0, x.size(2)-1), torch.clamp(q_rb[..., N:], 0, x.size(3)-1)], dim=-1).long()
    # 用q_lt的前半部分坐标q_lt_x和q_rb的后半部分q_rb_y组合成q_lb
    q_lb = torch.cat([q_lt[..., :N], q_rb[..., N:]], dim=-1)
    # dim=-1即按照维度N进行concat
    # 同理
    q_rt = torch.cat([q_rb[..., :N], q_lt[..., N:]], dim=-1)

    # 将p的坐标也要限制在图像范围内
    p = torch.cat([torch.clamp(p[..., :N], 0, x.size(2)-1), torch.clamp(p[..., N:], 0, x.size(3)-1)], dim=-1)

    # bilinear kernel (b, h, w, N)
    # 双线性插值的4个系数
    g_lt = (1 + (q_lt[..., :N].type_as(p) - p[..., :N])) * (1 + (q_lt[..., N:].type_as(p) - p[..., N:]))
    g_rb = (1 - (q_rb[..., :N].type_as(p) - p[..., :N])) * (1 - (q_rb[..., N:].type_as(p) - p[..., N:]))
    g_lb = (1 + (q_lb[..., :N].type_as(p) - p[..., :N])) * (1 - (q_lb[..., N:].type_as(p) - p[..., N:]))
    g_rt = (1 - (q_rt[..., :N].type_as(p) - p[..., :N])) * (1 + (q_rt[..., N:].type_as(p) - p[..., N:]))

    # (b, c, h, w, N)
    # 现在只获取了坐标值，我们最终目的是获取相应坐标上的值，
    # 这里我们通过self._get_x_q()获取相应值。
    # x：
    # q_lt：[B, H, W, 2N]
    x_q_lt = self._get_x_q(x, q_lt, N)
    x_q_rb = self._get_x_q(x, q_rb, N)
    x_q_lb = self._get_x_q(x, q_lb, N)
    x_q_rt = self._get_x_q(x, q_rt, N)

    # (b, c, h, w, N)
    # 双线性插值计算
    x_offset = g_lt.unsqueeze(dim=1) * x_q_lt + \
               g_rb.unsqueeze(dim=1) * x_q_rb + \
               g_lb.unsqueeze(dim=1) * x_q_lb + \
               g_rt.unsqueeze(dim=1) * x_q_rt

    # modulation
    if self.modulation:
        m = m.contiguous().permute(0, 2, 3, 1)
        m = m.unsqueeze(dim=1)
        m = torch.cat([m for _ in range(x_offset.size(1))], dim=1)
        x_offset *= m

    # 在获取所有值后我们计算出x_offset，但是x_offset的size
    # 是(b,c,h,w,N)，我们的目的是将最终的输出结果的size变
    # 成和x一致即(b,c,h,w)，所以在最后用了一个reshape的操作。
    # 这里ks=3
    x_offset = self._reshape_x_offset(x_offset, ks)
    out = self.conv(x_offset)

    return out

6 学习笔记

6.1 有一点疑惑的是，p_conv生成的offset跟特征向量x没有发生四则运算，而只是有索引运算那么，梯度是如何传递的呢？

有一天我在公交车上思考关于DCN的变形时，想到：p_conv生成的offset跟特征向量x没有发生四则运算，而只是有索引运算那么，那么梯度是如何传递的呢？
我猜想：可能时索引操作可以传递梯度，有两种可能，

• x[index]操作可以传递梯度
• x.gather()函数可以传递梯度

现在，我们通过实验来验证一下索引操作是否可以传递梯度，……
我在知乎中关于这个问题进行了提问——“关于 DCN 中的 p_conv 是如何获得梯度更新的？”；不过暂时没有同学回答；
我在这里对之前的探究进行一下总结：我感觉，总的来说，DCNv2虽然叫做“可变形卷积”，实际上它无法真正进行变形，很有可能这里的p_conv根本无法获得参数更新，实际上只是通过随机初始化形成了多个随机大小的感受野，也就是说p_conv中有多个随机大小的偏移从而有不同形状的卷积核，然后根据蒙特卡洛的思想来学习不同偏移的卷积核，总的来说，所谓的“可变形卷积”实际上无法进行变形，而只是具有多个不同形状的卷积核罢了。