7.1 过拟合

什么是过拟合呢？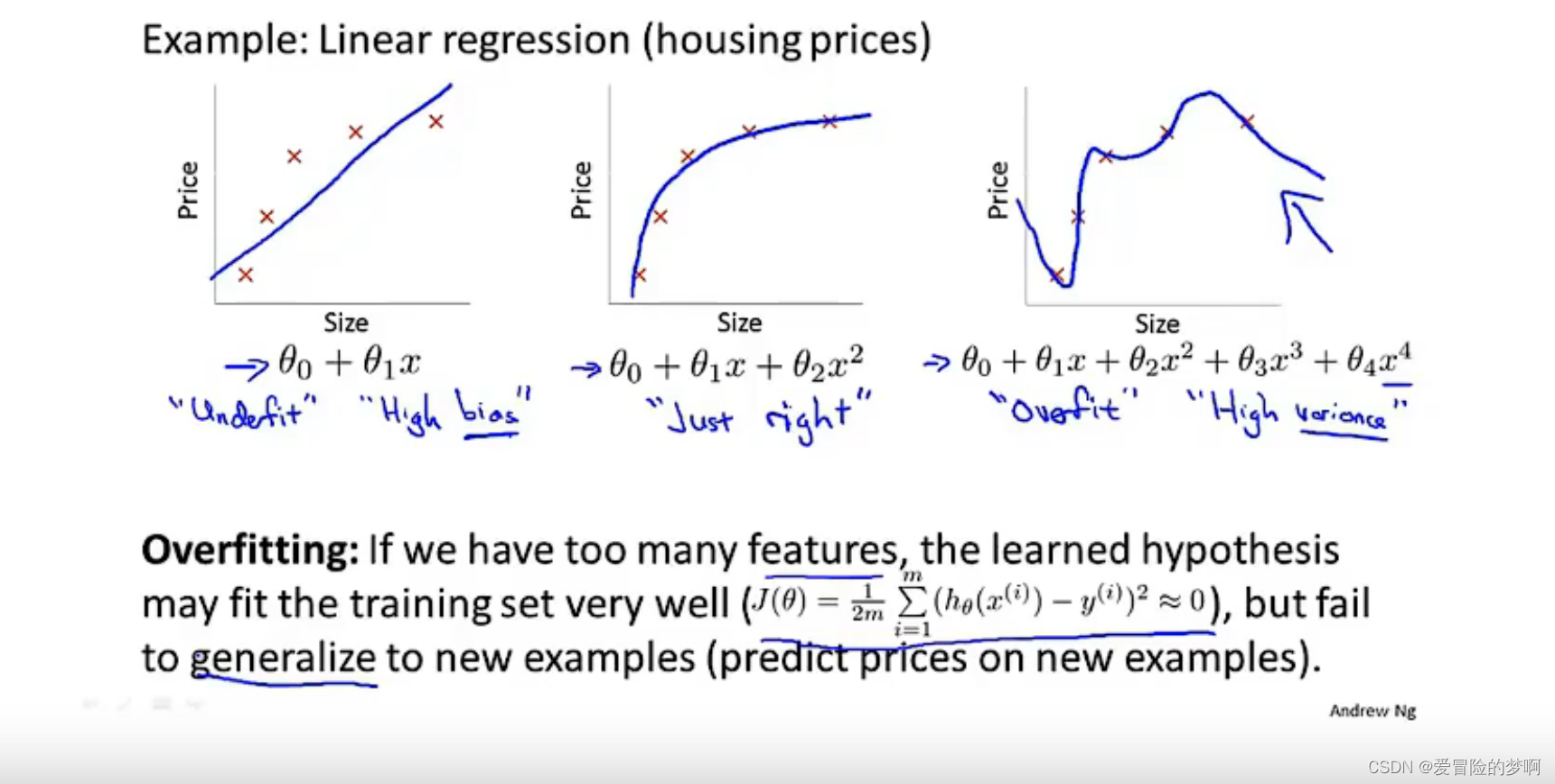

我们还是以房价预测为例子，对于图1来说，我们找到一条曲线来拟合房价，但是随着size的越来越大，价格的增长速度减小了，所以曲线不能很好的拟合，通常称这样的曲线叫做欠拟合，或者叫做有很高的偏差。

第二个图加上了二次函数来拟合，我们可以看到如图所示能够很好的去拟合图像。

第三个图我们加上了很多复杂的多项式，我们可以看到如图所示，看起来拟合程度更高，但是他是一条扭曲的图像，它不停的上下波动，事实上我们不认为这是一条预测房价很好的模型，我们称这种问题叫做过度拟合，另一种说法是这个算法具有高方差 。对于多项式函数来拟合数据，就会面临着可能的函数太过庞大，变量太多的问题，我们没有足够的数据来约束它，这就叫过拟合。

通常来说过拟合的问题将会出现在变量过多的时候出现，这时候代价函数可能为0，因为拟合的太好了。这里的泛化能力是指模型应用到新样本的能力。

同样过拟合也会在逻辑回归中出现。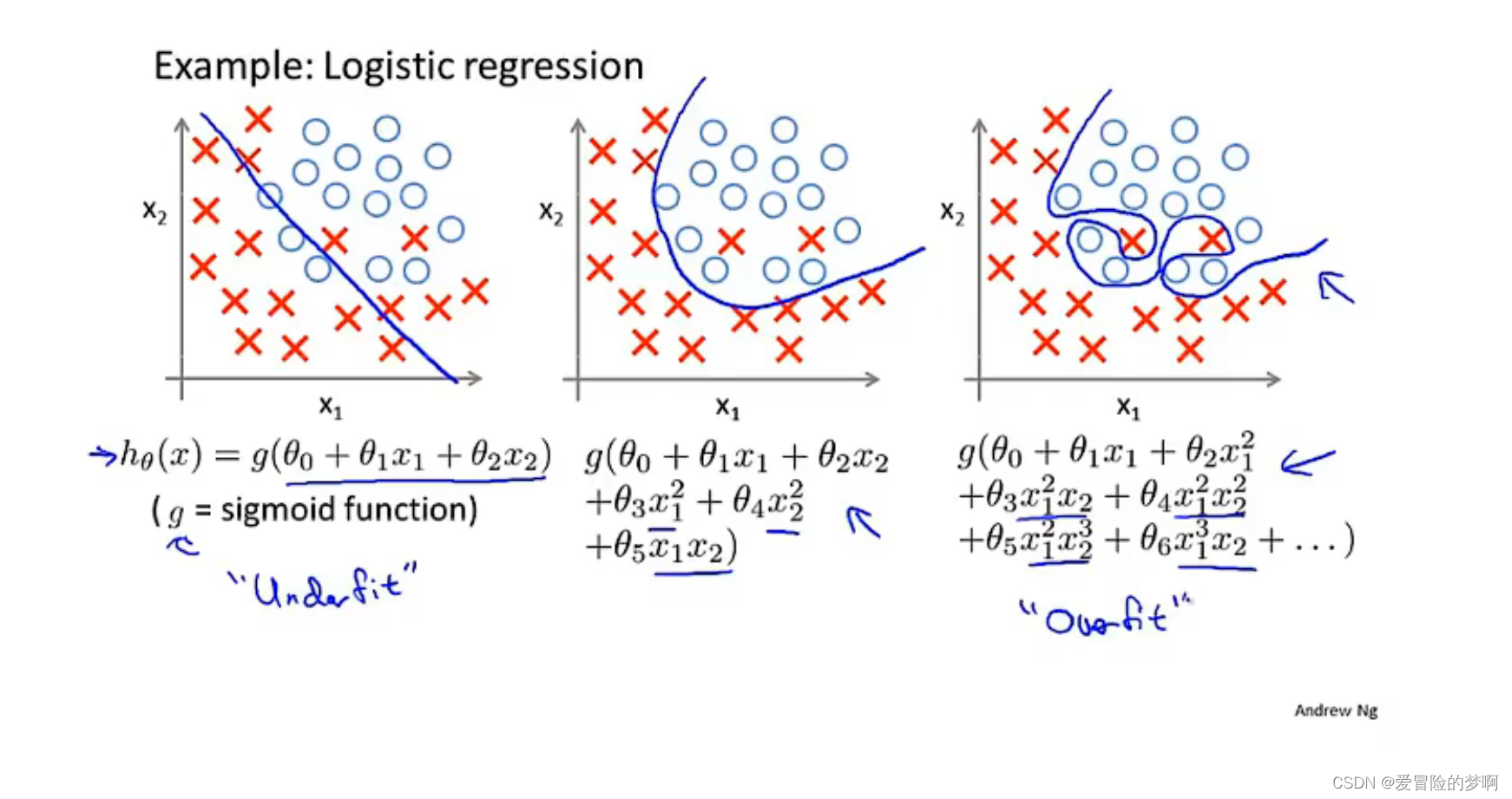

下面介绍解决过拟合的问题。

对于房价预测例子来说，我们可能会有很多特征，他们或多或少的都会对房子价格有影响，如果出现特征过多，但是数据样本又少，很大情况会出现过拟合的现象。

为了解决过拟合，通常两种方法，1.减少选择过多的特征,就是选择合适数量的特征。缺点就是舍弃一部分特征，对数据的预测程度可能有影响。
2.正则化，我们保留所有的特征，但是减少量级或者参数θj的大小。

7.2 代价函数

在这节中将会介绍正则化是如何运行的，在进行正则化的时候，我们还会写出相应的代价函数。

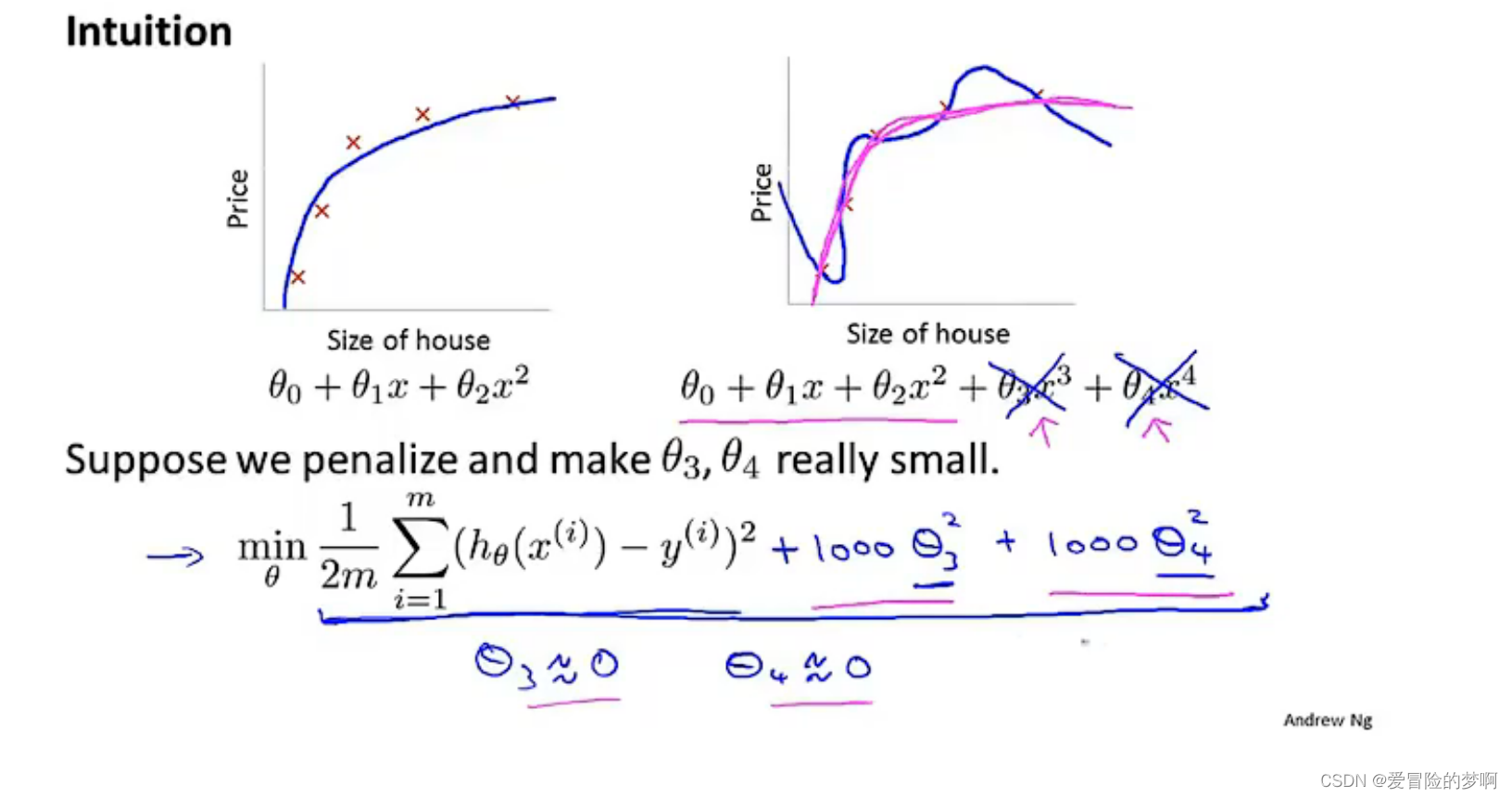
上面这个例子，对于第二个图它是过拟合的，我们不妨在函数中加上惩罚项使得参数θ3和4都很小，比如下面这个式子，他的系数都是1000（图中的加上1000的θ3和4就是惩罚项），为了最小化这个代价函数，我们做的就是使θ3和4越小越好，接近于0最好。

这种思想就是正则化的思想。
如果我i们的参数值较小，它意味着一个更简单的假设模型。

在下面这个房屋预测的例子中，对于100个参数，正则化的作用就是对代价函数，就是线性回归中的代价函数进行修改，来缩小所有的参数，因为这里我们不知道该选哪些参数进行缩小，所以在代价函数后面添加一个新的项，也就是正则化项来缩小每一个参数，它的作用就是缩小每一个参数。顺便说一下，这个惩罚项就是求和是从θ1开始的，也就是没有给θ0加惩罚项，这是约定俗成的，只对从1到n进行求和。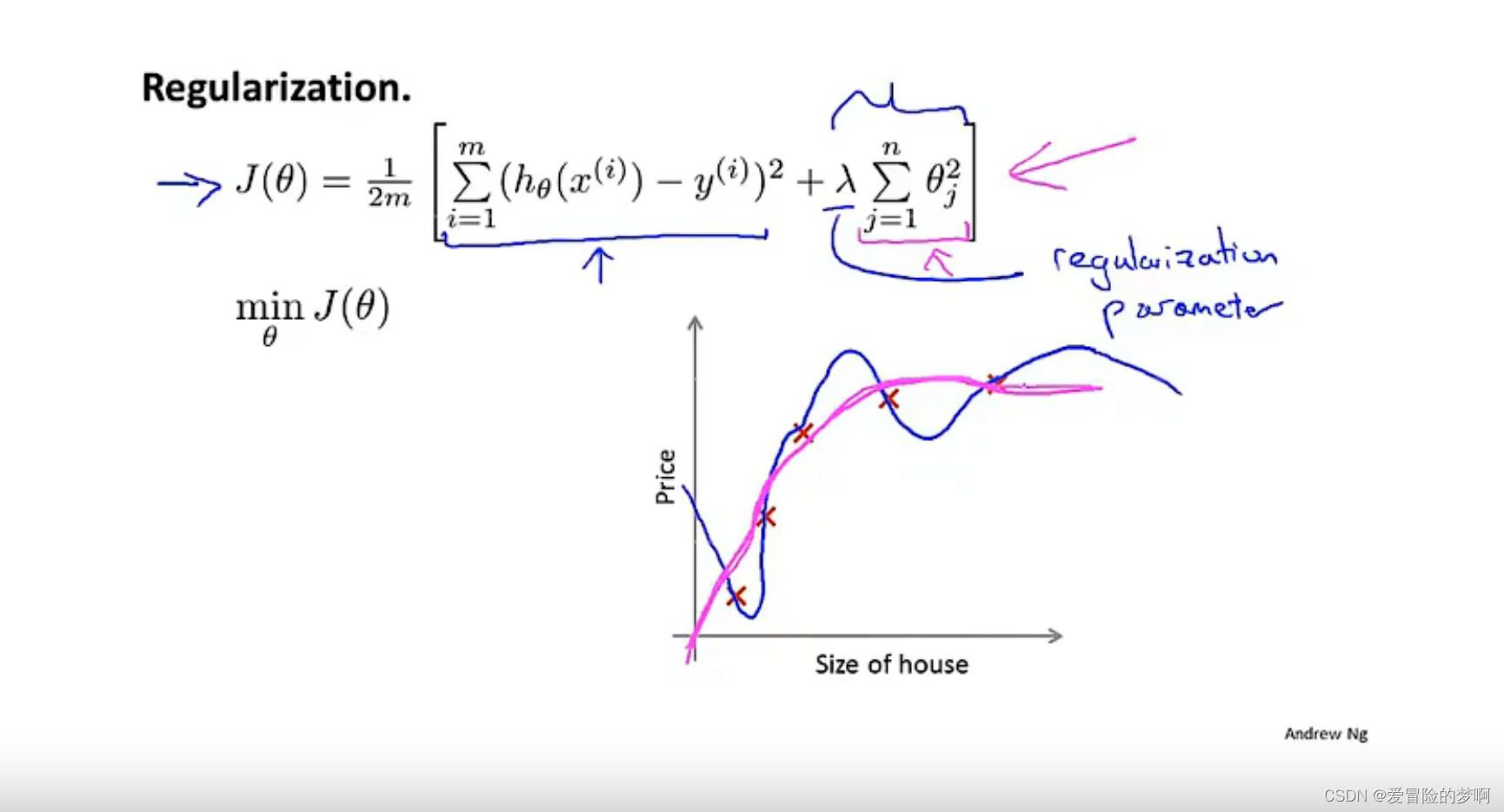

λ称为正则化参数，他的作用就是控制两个不同目标之间的取舍，第一个目标与目标函数的第一项有关，也就是我们想去训练想去更好的拟合数据，更好的拟合数据集，第二个目标就是要保持参数尽量的小与目标函数第二项有关，与正则化目标有关，所以这个参数的作用就是对这两个目标进行权衡trade-off，即更好的拟合数据和参数控制得更小的目标，从而保持假设模型的相对简单，避免出现过拟合现象。

如果这个参数设置的过大的话，也就是对参数的惩罚过大，最后所有的参数都会接近于0，这样的话相当于把所有的参数都忽略了，最后只剩下个θ0，也就变成一条直线了，它并没有贴近太多的数据集。换句话说就是这个假设模型的偏见性太强或者说偏差过高。

7.3 线性回归的正则化

这个是线性回归中梯度下降中加入了正则化的方法，因为正则化项是对θ1到n的惩罚，这里单独拿出来了θ0进行梯度下降（也就是第一行θ0的一行），下面这个θj的式子是求梯度后得到的（并且是对thetaj求导，其他的theta是0），后面的惩罚项也是求完导的，所以求和符号啊，平方啊都没了。

我们可以把上面的式子整理下，提取出来θj，这里括号中的1-α什么的是小于1的，因为α学习率很小，m很大，α×λ是比m小的，所以是小于1的。那么thetaj的更新结果就是就是小于1的thetaj，例如我们假设为0.99thetaj，也就是把thetaj向0的方向缩小了一点点，这使得thetaj变小了一点点；减去的后面一项呢？我们可以看到减去的后面一项其实就是和之前我们没有添加正则项之前的梯度下降更新一样。所以每次迭代更新就是把thetaj缩小一点。

梯度下降只是我们拟合线性回归模型时候所讲的算法之一，下一个就是用正则方程来解决。

对于下面这个正则方程，矩阵X每一行代表着一个单独训练样本，向量y代表m维的向量，它包含了训练集里面的所有标签，所以X是m×（n+1）的矩阵。

为了最小化代价函数J，我们发现一个式子，让J等于图中的式子，这样计算出来的theta可以使得代价函数J（θ）最小化，这时J（θ）是没有正则项的。我们现在用正则化来得到我们想要的最小值，方法就是将对各个参数偏导数设为0，然后进行一些数学推导，最后得到如图所示的式子，使得代价函数最小。式子里面的矩阵实际就是除了对角线第一个为0（为了theta0不正则化），其他为1的矩阵，这个矩阵是（n+1）×（n+1）的矩阵。

7.4 逻辑回归的正则化

对于逻辑回归来说，逻辑回归的代价函数如下图所示，对于这个h(θ)函数如下所示，对代价函数进行正则化操作，正则项惩罚theta1-n

经历梯度下降后式子如下图所示，我们看这和之前的式子应该是差不多的，但是这里的假设函数是不一样的，中括号里面的是对J(theta)的求导