Title

题目

Self-consistent recursive diffusion bridge for medical image translation

医学图像转换的自洽递归扩散桥

01

文献速递介绍

多模态医学图像与医学图像转换相关研究进展 在多种模态下获取的医学图像，能够捕捉到人体组织互补的诊断信息（Iglesias 等人，2013；Lee 等人，2017），但实施多模态成像方案会带来高昂的经济成本与人力成本，因而具有一定负担（Ye 等人，2013；Huynh 等人，2016；Jog 等人，2017；Joyce 等人，2017）。在不增加成本的前提下拓展基于成像的评估范围，一种有效的方法是医学图像转换——即从已获取的源模态图像中预测未获取的目标模态图像（Cordier 等人，2016；Wu 等人，2016；Zhao 等人，2017；Huang 等人，2018）。 图像转换的重要临床应用场景包括：为降低冗余度、提高扫描效率，对成像方案中未纳入的、具有更高诊断冗余信息的目标模态进行补全；从无创源模态中补全有创目标模态，以避免注射有害造影剂或暴露于电离辐射（Lee 等人，2019）；在回顾性成像研究中，补全成像方案中缺失的目标模态，以提高不同受试者间成像方案的一致性（Clark 等人，2019）。尽管如此，医学图像转换本质上是一项极具挑战性的任务——同一组织在不同模态下的信号强度会呈现非线性变化，而这种变化难以通过解析方式表征（Roy 等人，2013；Alexander 等人，2014；Huang 等人，2017）。因此，擅长解决非线性问题的基于学习的方法，近年来已成为医学图像转换领域的主流框架（Van Nguyen 等人，2015；Vemulapalli 等人，2015；Sevetlidis 等人，2016；Nie 等人，2016）。 基于学习的方法通常旨在捕捉“给定源图像时目标图像分布”的条件先验，不过不同方法学习该先验的方式存在差异（Bowles 等人，2016；Chartsias 等人，2018；Nie 等人，2018；Yang 等人，2018；Wei 等人，2019）。在现有方法中，生成对抗网络（GAN）因能合成极具真实感的目标图像而被广泛应用（Yu 等人，2018；Armanious 等人，2019；Li 等人，2019；Dar 等人，2019b；Yu 等人，2019），并在多对比度磁共振成像（MRI）（Kim 等人，2021；Yurt 等人，2021；Hu 等人，2022；Xia 等人，2023；Han 等人，2023；Zhang 等人，2025）、磁共振成像-计算机断层扫描（MRI-CT）转换（Jin 等人，2019；Dalmaz 等人，2022；Gu 等人，2023；Xin 等人，2024）等多种任务中取得了成功。然而，GAN 通过生成器与判别器的交互捕捉隐式先验，易受训练不稳定性影响，这往往会降低图像保真度（Wang 等人，2020；Zhou 等人，2020）。与此相反，近年来有研究采用去噪扩散模型（DDM）捕捉显式先验，从而提升了训练稳定性（Özbey 等人，2023；Meng 等人，2022；Lyu 和 Wang，2022；Wang 等人，2024）。 DDM 会执行一个正向过程：通过反复添加高斯噪声逐步破坏目标图像，直至得到纯噪声图像这一渐近终点（图 1a）。为恢复目标图像，需通过恢复网络执行反向过程——该网络在将源图像作为独立静态输入的同时，逐步对随机噪声图像进行去噪（Ho 等人，2020）。由于正向过程完全不依赖源模态，反向过程被设计为在源模态的间接引导下，学习从噪声图像到目标图像的去噪变换（Özbey 等人，2023）。在每个反向扩散步骤中，恢复网络都需在“与任务无关的去噪变换”和“与任务相关的源-目标图像变换”之间进行权衡，这可能导致对源模态引导的强调不足或过度（Song 等人，2021；Güngör 等人，2023）。因此，由于去噪变换与源-目标变换存在差异，DDM 可能面临转换性能欠佳的问题（Liu 等人，2023a）。 为增强基于扩散先验的任务相关性，一种新兴方法是采用扩散桥——它能够在两种不同模态间直接进行转换（Delbracio 和 Milanfar，2023；Chung 等人，2023）。具体而言，扩散桥分别基于目标图像和源图像定义正向过程的起点和终点（图 1b）。由于连接两种模态的成像算子通常未知，中间步骤的图像样本需从正态分布中获取，该正态分布的均值为起点与终点的凸组合（Liu 等人，2023a；Kim 等人，2024a）。反向过程从源图像开始采样，逐步将源图像映射为目标图像。近期已有少数成像研究成功将扩散桥应用于单模态图像重建——从因欠采样、低分辨率等因素导致的退化测量数据中重建图像（Mirza 等人，2023；Kim 和 Ye，2024；Kim 等人，2024b）。然而，扩散桥在医学图像转换中的潜力尚未得到充分探索，现有方法仍面临多项关键挑战：常规扩散桥采用的噪声调度策略规定“起点和终点处噪声方差为零、扩散过程中点附近噪声方差较高”（Su 等人，2023）。终点处的零方差会形成“源模态硬先验”，对应训练集中以源图像为中心的确定性狄拉克δ分布，这会降低模型对“由测量噪声导致的源图像变异性”的鲁棒性（图 2a）；同时，中点处的高方差可能会中断源模态与目标模态在扩散过程中的信息传递。此外，扩散桥通常对中间样本进行“一次性估计”，这限制了生成图像的采样精度（Peng 等人，2022）。 在此，我们提出一种新型自洽递归扩散桥（SelfRDB），以提升多模态医学图像转换的性能。与常规扩散桥不同，SelfRDB 在其正向过程中采用了新型噪声调度策略——噪声方差朝着“含噪声源图像”对应的终点单调递增（图 1c）。通过这种方式，它能够捕捉“源模态软先验”，从而提高对测量噪声的鲁棒性；同时，通过规定扩散过程中点附近的低方差，促进模态间的信息传递（图 2b）。为避免在含噪声终点处丢失组织信息，SelfRDB 的恢复网络在反向过程中采用原始源图像的固定引导。最后，为提高每个反向步骤的采样精度，SelfRDB 针对目标图像采用了新型“自洽递归估计算法”，并利用该自洽估计值合成精度更高的中间样本（图 3）。 我们在多对比度 MRI 转换和 MRI-CT 转换任务中进行了全面验证。结果表明，SelfRDB 的性能显著优于主流生成对抗网络、扩散模型（包括现有扩散桥）。SelfRDB 的代码可在 https://github.com/icon-lab/SelfRDB 获取。 ## 研究贡献 1. 据我们所知，SelfRDB 是文献中首个用于不同模态间医学图像转换的扩散桥。 2. SelfRDB 采用新型正向扩散过程，通过捕捉源模态软先验，提高了对测量噪声的鲁棒性，并促进了源-目标模态间的信息传递。 3. SelfRDB 采用新型自洽递归估计算法，提升了反向扩散步骤中的采样精度。

Abatract

摘要

Denoising diffusion models (DDM) have gained recent traction in medical image translation given their hightraining stability and image fidelity. DDMs learn a multi-step denoising transformation that progressivelymaps random Gaussian-noise images provided as input onto target-modality images as output, while receivingindirect guidance from source-modality images via a separate static channel. This denoising transformationdiverges significantly from the task-relevant source-to-target modality transformation, as source images aregoverned by a non-noise distribution. In turn, DDMs can suffer from suboptimal source-modality guidance andperformance losses in medical image translation. Here, we propose a novel self-consistent recursive diffusionbridge (SelfRDB) that leverages direct source-modality guidance within its diffusion process for improvedperformance in medical image translation. Unlike DDMs, SelfRDB devises a novel forward process with thestart-point taken as the target image, and the end-point defined based on the source image. Intermediateimage samples across the process are expressed via a normal distribution whose mean is taken as a convexcombination of start-end points, and whose variance is controlled by additive noise. Unlike regular diffusionbridges that prescribe zero noise variance at start-end points and high noise variance at mid-point of theprocess, we propose a novel noise scheduling with monotonically increasing variance towards the end-point inorder to facilitate information transfer between the two modalities and boost robustness against measurementnoise. To further enhance sampling accuracy in each reverse step, we propose a novel sampling procedurewhere the network recursively generates a transient-estimate of the target image until convergence onto aself-consistent solution. Comprehensive experiments in multi-contrast MRI and MRI-CT translation indicatethat SelfRDB achieves state-of-the-art results in terms of image quality

去噪扩散模型（DDM）凭借其较高的训练稳定性和图像保真度，近年来在医学图像转换领域受到广泛关注。DDM会学习一种多步去噪变换，该变换能逐步将作为输入的随机高斯噪声图像映射为目标模态图像作为输出，同时通过一个独立的静态通道接收来自源模态图像的间接引导。由于源图像受非噪声分布支配，这种去噪变换与任务相关的“源模态-目标模态”变换存在显著差异。由此，DDM在医学图像转换中可能面临源模态引导效果欠佳及性能损失的问题。 在此，我们提出一种新型自洽递归扩散桥（SelfRDB），该模型在其扩散过程中利用直接的源模态引导，以提升医学图像转换性能。与DDM不同，SelfRDB设计了一种新型正向过程：将起点设为目标图像，终点则基于源图像定义。过程中的中间图像样本通过正态分布表示，该正态分布的均值为起点与终点的凸组合，方差由加性噪声控制。不同于常规扩散桥（其规定起点和终点的噪声方差为零、过程中点的噪声方差较高），我们提出一种新型噪声调度策略——噪声方差朝着终点单调递增，以促进两种模态间的信息传递，并增强对测量噪声的鲁棒性。 为进一步提高每个反向步骤中的采样精度，我们提出一种新型采样流程：网络会递归生成目标图像的瞬时估计值，直至收敛到自洽解。在多对比度磁共振成像（MRI）及磁共振成像-计算机断层扫描（MRI-CT）转换任务中的全面实验表明，SelfRDB在图像质量方面取得了最先进的结果。

Method

方法

3.1. Diffusion bridges

Diffusion bridges are a general framework to describe the evolutionbetween two arbitrary probability distributions across a finite timeinterval 𝑡 ∈ [0, 𝑇 ] (Liu et al., 2023a). In the context of mapping asource image 𝒙*𝑇* ∶= 𝒚 onto a target image 𝒙0 , the learning objectivefor diffusion bridges can be expressed as:min𝑝∈[0, 𝑇* ]𝐷KL(𝑝* ∥ 𝑞), s.t. 𝑝0 = 𝑝target, 𝑝**𝑇 = 𝑝source,(1)where [0, 𝑇 ] is the space of path measures with marginal densitiesfor the target and source (𝑝0 = 𝑝target and 𝑝**𝑇 = 𝑝source) taken asboundary conditions, and 𝑞 is the reference path measure. Solution of(1) is the optimal path measure 𝑝 ∗ ∈ [0, 𝑇 ] that can be described via thefollowing forward-reverse stochastic differential equations (Chen et al.,2021):d𝒙𝑡 = [𝒇 + 𝑔 2∇ log𝛹(𝒙𝑡 , 𝑡)]d𝑡 + 𝑔d𝒘𝑡 , 𝒙0 ∼ 𝑝target,d𝒙𝑡 = [𝒇 − 𝑔 2∇ log𝛹̄ (𝒙𝑡 , 𝑡)]d𝑡 + 𝑔d𝒘 𝑡 , 𝒙𝑇 ∼ 𝑝source. (2)Here, 𝒇 is the drift coefficient, 𝑔 is the diffusion coefficient, 𝒘𝑡 , 𝒘 𝑡are forward-reverse Wiener processes, and ∇ log𝛹(𝒙𝑡 , 𝑡), ∇ log ̄𝛹(𝒙𝑡 , 𝑡)are nonlinear forward-reverse drift terms related to the score function ∇ log 𝑝𝑡 (𝒙𝑡 ) (Nelson, 1967). In contrast to DDMs based on lineardrifts (Song et al., 2020), the nonlinear drifts in diffusion bridges enablethe use of non-Gaussian 𝑝source. A Dirac-delta distribution is assumed forthe target modality, i.e., 𝑝0 (⋅) ∶= 𝛿**𝑥 (⋅), such that the marginal densityat the start-point is taken as 𝑝0 (𝒙0 ) = 1 given a (target, source) imagepair (𝒙0 , 𝒙𝑇 ). This assumption ensures computational tractability bydecoupling the constraints in Eq. (2) (Liu et al., 2023a).In regular diffusion bridges, high-quality image pairs from targetand source modalities are taken as start- and end-points of the diffusionprocess as in Eq. (1), with zero additive-noise variance at 𝑡 = 0 and𝑡* = 𝑇 (Fig. 1b). This choice ensures optimal transport for training data,and enables the bridge to directly translate high-quality source imagesduring inference (Liu et al., 2023a). However, it also constrains thebridge to capture a hard-prior on the source modality, since the end-pointfollows a Dirac-delta distribution based on source images in the trainingset, i.e., 𝑝𝑇 (𝒙𝑇 ) = 1 given a training pair (𝒙0 , 𝒙𝑇 ). Combined with highnoise variance near 𝑡 = 𝑇 ∕2, this distributional constraint can compromise generalization and information transfer from source-to-targetimages (Fig. 2a).

3.1 扩散桥 扩散桥是描述有限时间区间𝑡 ∈ [0, 𝑇]内两个任意概率分布之间演变过程的通用框架（Liu 等人，2023a）。在将源图像𝒙𝑇 ∶= 𝒚映射到目标图像𝒙₀的场景下，扩散桥的学习目标可表示为：  其中，$\mathcal{P}[0, T]$ 是路径测度空间，其边缘密度以目标模态和源模态的概率分布（$p_0 = p{\text{target}}$ 且 $p_T = p{\text{source}}$）作为边界条件；$q$ 是参考路径测度。式（1）的解为最优路径测度 $p^* \in \mathcal{P}[0, T]$，该测度可通过以下正向-反向随机微分方程描述（Chen 等人，2021）： \begin{aligned} d\boldsymbol{x}t &= \left[\boldsymbol{f} + g^2 \nabla \log \Psi(\boldsymbol{x}t, t)\right]dt + g d\boldsymbol{w}t, \quad \boldsymbol{x}0 \sim p{\text{target}}, \ d\boldsymbol{x}t &= \left[\boldsymbol{f} - g^2 \nabla \log \bar{\Psi}(\boldsymbol{x}t, t)\right]dt + g d\bar{\boldsymbol{w}}t, \quad \boldsymbol{x}T \sim p{\text{source}}. \tag{2} \end{aligned} 式中，𝒇 为漂移系数，$g$ 为扩散系数，$\boldsymbol{w}t$、$\bar{\boldsymbol{w}}t$ 为正向-反向维纳过程，$\nabla \log \Psi(\boldsymbol{x}t, t)$、$\nabla \log \bar{\Psi}(\boldsymbol{x}t, t)$ 是与分数函数 $\nabla \log p_t(\boldsymbol{x}t)$ 相关的非线性正向-反向漂移项（Nelson，1967）。与基于线性漂移的去噪扩散模型（DDM）（Song 等人，2020）不同，扩散桥中的非线性漂移允许使用非高斯分布的 $p{\text{source}}$。 假设目标模态服从狄拉克δ分布，即 $p_0(\cdot) \coloneqq \delta_x(\cdot)$，则对于给定的（目标图像，源图像）对（𝒙₀, 𝒙𝑇），起点处的边缘密度满足 $p_0(\boldsymbol{x}0) = 1$。该假设通过解耦式（2）中的约束条件，保证了计算的可处理性（Liu 等人，2023a）。 在常规扩散桥中，如式（1）所示，目标模态与源模态的高质量图像对被视为扩散过程的起点和终点，且在 $t=0$ 和 $t=T$ 处加性噪声方差为零（图 1b）。这种设计确保了训练数据的最优传输，且能使扩散桥在推理阶段直接对高质量源图像进行转换（Liu 等人，2023a）。然而，这也将扩散桥约束为捕捉“源模态硬先验”——因为终点服从基于训练集中源图像的狄拉克δ分布，即对于训练图像对（𝒙₀, 𝒙𝑇），有 $p_T(\boldsymbol{x}_T) = 1$。结合 $t=T/2$ 附近的高噪声方差，这种分布约束可能会损害模型的泛化能力，以及源图像到目标图像的信息传递（图 2a）。

Conclusion

结论

In this study, we introduced a novel diffusion bridge, SelfRDB,for multi-modal medical image translation tasks. SelfRDB learns atask-relevant progressive transformation between source- and targetmodality distributions. In reverse diffusion steps, it improves imagefidelity via a self-consistent recursive estimation procedure and stationary guidance from the acquired source image. It further employsa monotonically-increasing scheduling for the noise variance towardsthe source image in order to facilitate information transfer betweenthe modalities, and to build a soft prior on the source modality thatenhances noise robustness. With these technical advances, SelfRDBachieves state-of-the-art image quality compared to leading GAN anddiffusion methods, so it holds great promise for medical image translation applications.

本研究内容翻译 在本研究中，我们提出了一种新型扩散桥梁（diffusion bridge）模型SelfRDB，用于多模态医学图像转换任务。该模型能够学习源模态与目标模态分布之间与任务相关的渐进式转换。在反向扩散步骤中，SelfRDB通过自一致性递归估计过程，以及来自所获取源图像的固定引导，提升图像保真度。此外，该模型还对源图像的噪声方差采用单调递增调度策略，以促进模态间的信息传递，并在源模态上构建软先验，从而增强噪声鲁棒性。凭借这些技术改进，与主流生成对抗网络（GAN）及扩散模型相比，SelfRDB实现了当前最优（state-of-the-art）的图像质量，因此在医学图像转换应用中具有广阔前景。

Figure

图

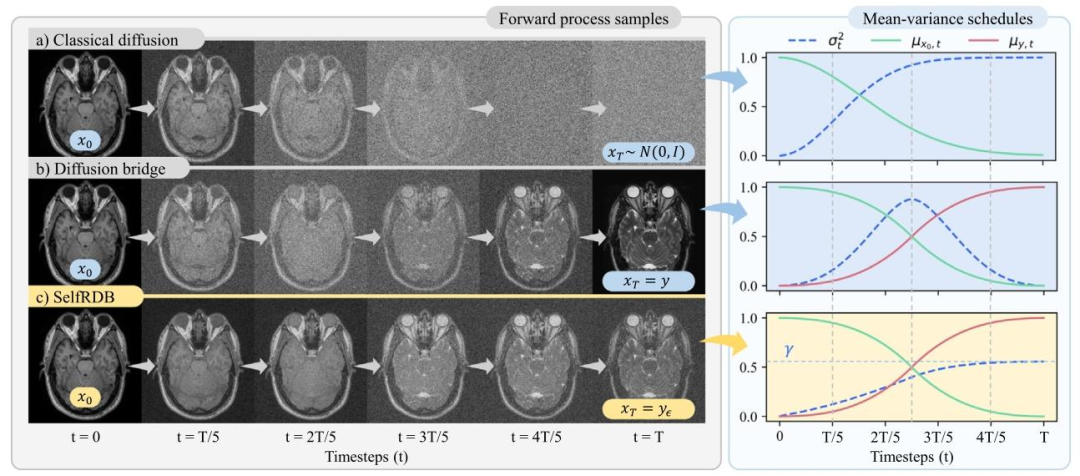
Fig. 1. Diffusion methods commonly take the target image as the start-point 𝒙0 of the diffusion process, albeit they can differ in expression of image samples in remainingtimesteps. Illustrations of images across the forward process are depicted along with underlying schedules for the mean (𝜇𝑥0,𝑡, 𝜇𝑦,𝑡) and noise variance (𝜎𝑡 2 ). (a) Classical diffusion:DDMs use a white-Gaussian noise image as an asymptotic end-point 𝒙*𝑇* ∼ 𝑁(0, 𝐼). Intermediate samples are obtained by adding increasing levels of random Gaussian noise ontothe target image. (b) Regular diffusion bridge: Regular bridges use the source image as a finite end-point, 𝒙𝑇 = 𝒚. Intermediate samples are taken as a convex combination ofsource–target images, corrupted with additive noise. Noise variance is zero at start- and end-points, and it peaks at the mid-point. (c) Proposed: SelfRDB is a novel diffusionbridge that uses a noise-added source image as the end-point, 𝒙𝑇 = 𝒚𝜖 . Intermediate samples still depend on a convex combination of source–target images, yet SelfRDB uniquelyprescribes monotonically-increasing noise variance towards the end-point.

 图1 不同扩散方法的正向过程对比 扩散方法通常以目标图像作为扩散过程的起点𝒙₀，但在其余时间步的图像样本表示方式上存在差异。图中展示了正向过程中不同时间步的图像示例，以及均值（𝜇ₓ₀,ₜ、𝜇ᵧ,ₜ）和噪声方差（𝜎ₜ²）的底层调度策略。 (a) 经典扩散（Classical diffusion）：   去噪扩散模型（DDM）以白高斯噪声图像作为渐近终点𝒙𝑇 ∼ 𝒩(0, 𝐼)。中间样本通过向目标图像添加强度逐渐增加的随机高斯噪声得到。 (b) 常规扩散桥（Regular diffusion bridge）：   常规扩散桥以源图像作为有限终点，即𝒙𝑇 = 𝒚。中间样本为源图像与目标图像的凸组合，并叠加加性噪声。噪声方差在起点和终点处为零，在过程中点达到峰值。 (c) 所提方法（Proposed）：   自洽递归扩散桥（SelfRDB）是一种新型扩散桥，以含噪声源图像作为终点，即𝒙𝑇 = 𝒚𝜖。中间样本仍依赖于源图像与目标图像的凸组合，但SelfRDB的独特之处在于，其噪声方差朝着终点单调递增。

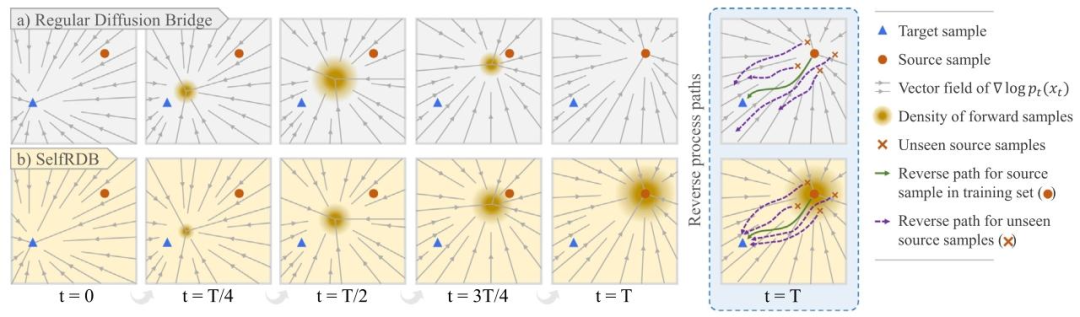
Fig. 2. Diffusion models learn the score function of the data through a multi-step transformation between the start- and end-points of the underlying diffusion process. Imagesamples are typically corrupted with Gaussian noise that smooths the data distribution by masking some of the original image features. Smoothing enables more uniform coverageof the data space in order to boost reliability against noise-induced variability. (a) Regular diffusion bridges use zero noise variance at the end-point constraining them to aDirac-delta distribution centered on the source images within the training set. This can compromise generalization performance to source images outside the training set (seepurple-colored dashed paths). (b) SelfRDB instead uses monotonically-increasing variance towards the end-point, so it is trained on noise-added source images. This improvesrobustness against variability in measurement noise levels of source images between training and test sets (see purple-colored dashed paths)

 图2 扩散模型分数函数学习与噪声方差对泛化性的影响 扩散模型通过底层扩散过程“起点-终点”间的多步变换，学习数据的分数函数。图像样本通常会被高斯噪声破坏——噪声通过掩盖部分原始图像特征，使数据分布更平滑。这种平滑处理能让模型更均匀地覆盖数据空间，从而提升对噪声诱导变异性的可靠性。 (a) 常规扩散桥（Regular diffusion bridges）：   其终点处噪声方差为零，这使得模型被约束在训练集中以源图像为中心的狄拉克δ分布上。这种特性可能会损害模型对“训练集外源图像”的泛化性能（参见紫色虚线路径）。 (b) 自洽递归扩散桥（SelfRDB）：   与之相反，SelfRDB的噪声方差朝着终点单调递增，因此模型在含噪声的源图像上进行训练。这一设计提升了模型对“训练集与测试集源图像测量噪声水平差异”的鲁棒性（参见紫色虚线路径）。

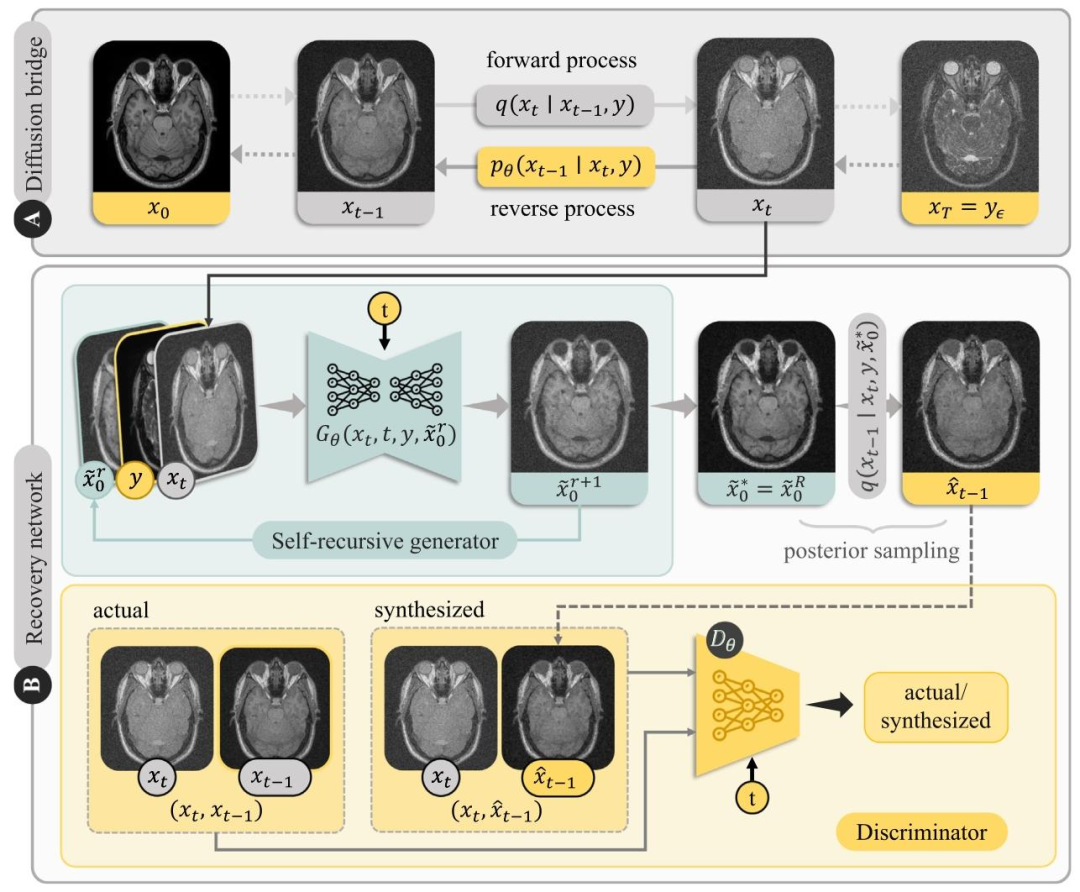
Fig. 3.SelfRDB casts a diffusion bridge between source and target images of an anatomy. (a) In the forward process, the start-point 𝒙0 is taken as the target image and theend-point 𝒙𝑇 is taken as a noise-added version of the source image 𝒚𝜖 . Intermediate image samples are derived via the forward transition probability 𝑞(𝒙𝑡 ∣ 𝒙𝑡−1, 𝒚), whose mean is aconvex combination of target–source images, and whose variance is driven by noise. In the reverse process, sampling is initiated on 𝒙𝑇 = 𝒚𝜖 , and intermediate samples are derivedvia the reverse transition probability 𝑝𝜃 (𝒙𝑡−1 ∣ 𝒙𝑡 , 𝒚𝜖 ). (b) Reverse diffusion steps are operationalized via a recovery network 𝐺𝜃 (𝒙𝑡, 𝑡, 𝒚, 𝒙*̃ 𝑟 0 ) that recursively generates a target-imageestimate 𝒙*̃𝑟 0 +1 at the current timestep, given the target-image estimate from the previous recursion 𝒙*̃𝑟 0 and the original source image 𝒚. Recursions are stopped upon convergenceonto a self-consistent solution 𝒙*̃ ∗ 0 = 𝐺𝜃 (𝒙𝑡 *, 𝑡,𝒚, 𝒙*̃ ∗ 0 ), which is then used for posterior sampling of 𝒙*̂* 𝑡−1 according to the normal distribution 𝑞(𝒙𝑡−1 ∣ 𝒙𝑡 , 𝒚, 𝒙*̃ ∗ 0 ). To improve posteriorsampling, a discriminator subnetwork 𝐷𝜃 (𝒙𝑡−1 or 𝒙*̂ 𝑡−1, 𝑡,𝒙𝑡 ) is used to perform adversarial learning on the recovered sample 𝒙*̂ 𝑡−1.

 图3 SelfRDB构建了同一解剖结构的源图像与目标图像之间的扩散桥梁 （a）在前向过程中，起点𝒙₀为目标图像，终点𝒙_𝑇为源图像的加噪版本𝒚_𝜖。中间图像样本通过前向转移概率𝑞(𝒙_𝑡 ∣ 𝒙_𝑡₋₁, 𝒚)生成，该概率的均值为目标-源图像的凸组合，方差由噪声控制。在反向过程中，从𝒙_𝑇 = 𝒚_𝜖开始采样，中间图像样本通过反向转移概率𝑝_𝜃(𝒙_𝑡₋₁ ∣ 𝒙_𝑡, 𝒚_𝜖)生成。   （b）反向扩散步骤通过恢复网络𝐺_𝜃(𝒙_𝑡, 𝑡, 𝒚, 𝒙*̃_0^𝑟)实现：给定前一轮递归得到的目标图像估计值𝒙*̃_0^𝑟和原始源图像𝒚，该网络在当前时间步递归生成目标图像估计值𝒙*̃_0^(𝑟+1)。当递归收敛到自一致解𝒙*̃_0^∗ = 𝐺_𝜃(𝒙_𝑡, 𝑡, 𝒚, 𝒙*̃_0^∗)时停止递归，随后根据正态分布*𝑞*(𝒙_𝑡₋₁ ∣ 𝒙_𝑡, 𝒚, 𝒙*̃_0^∗)对𝒙**̂_𝑡₋₁进行后验采样。为提升后验采样效果，判别器子网络*𝐷*_𝜃(𝒙_𝑡₋₁或𝒙*̂_𝑡₋₁, 𝑡, 𝒙_𝑡)用于对恢复样本𝒙*̂_𝑡₋₁进行对抗学习。

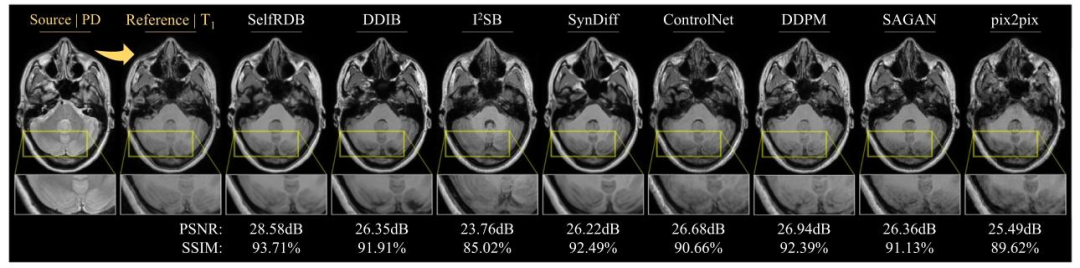
Fig. 4. Multi-contrast MRI translation for a representative PD→T1 task in the IXI dataset. Synthesized target images for competing methods are shown along with the referencetarget image (i.e., ground truth) and the input source image. Zoom-in display windows are used to highlight differences in synthesis performance

图4 IXI数据集上PD→T1代表性任务的多对比度MRI转换结果 本图展示了IXI数据集上“质子密度加权图像（PD）转换为T1加权图像（T1）”代表性任务的多对比度MRI转换效果。图中呈现了各对比方法生成的目标图像（合成T1图像），同时提供了参考目标图像（即真实值，ground truth）与输入源图像（PD图像）作为对照。为突出不同方法在合成性能上的差异，图中采用局部放大窗口（Zoom-in display windows）对关键区域进行细节展示，便于直观对比各方法在组织边缘、纹理细节等诊断相关特征上的合成精度。

Fig. 5. A visualization of RIIR inference on OASIS test split, visualized with a 2D slice and in-plane deformation. The inference step was set to 6 in both training and inference.All images in the same row were plotted using the same color range for better consistency

图5 OASIS测试集上RIIR推理结果可视化 本图采用二维切片（2D slice）与面内形变（in-plane deformation）的形式，展示了RIIR在OASIS测试集上的推理结果。训练与推理过程中，推理步数（inference step）均设为6。  

Fig. 6. Multi-modal MRI-CT translation for a representative T2→CT task in the pelvic dataset. Synthesized target images for competing methods are shown along with the referencetarget image (i.e., ground truth) and the input source image.

图6 盆腔数据集上T2→CT代表性任务的多模态MRI-CT转换结果 图中展示了盆腔数据集上“T2加权磁共振成像（MRI）转换为计算机断层扫描（CT）”这一代表性任务的多模态图像转换结果。除输入源图像和参考目标图像（即真实值，ground truth）外，还呈现了各对比方法生成的目标图像。

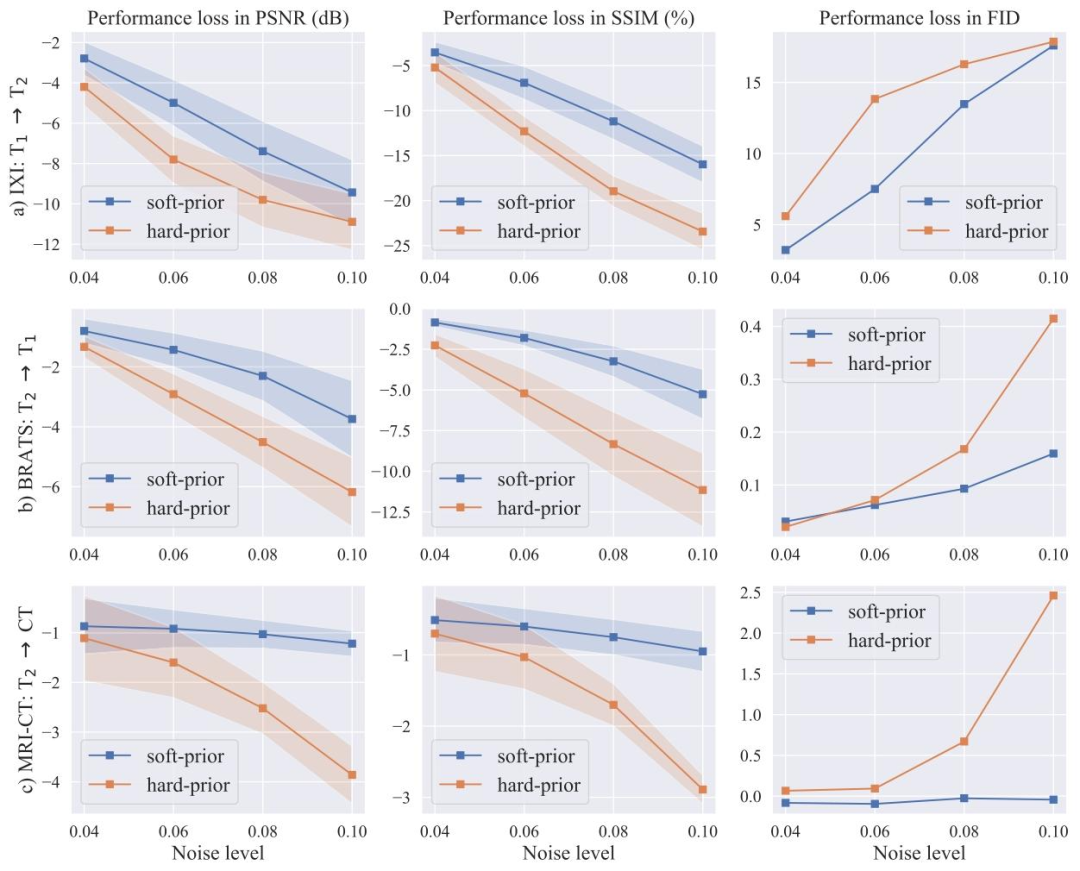
Fig. 7. Performance of soft-prior and hard-prior variants of SelfRDB in representative tasks. Models trained on original source images were tested on source images corrupted withvarying levels of additive noise. Performance losses in terms of PSNR (left column), SSIM (middle column) and FID (right column) are plotted in reference to the performancelevels based on original source images. Solid lines depict the average loss, and surrounding shaded regions depict the 65% confidence interval across the test set.

图7 SelfRDB的软先验和硬先验变体在代表性任务中的性能。在原始源图像上训练的模型，在被不同程度加性噪声破坏的源图像上进行测试。以基于原始源图像的性能水平为参考，绘制了峰值信噪比（PSNR，左列）、结构相似性指数（SSIM，中列）和弗雷歇初始距离（FID，右列）方面的性能损失。实线表示平均损失，周围的阴影区域表示测试集上的65%置信区间。

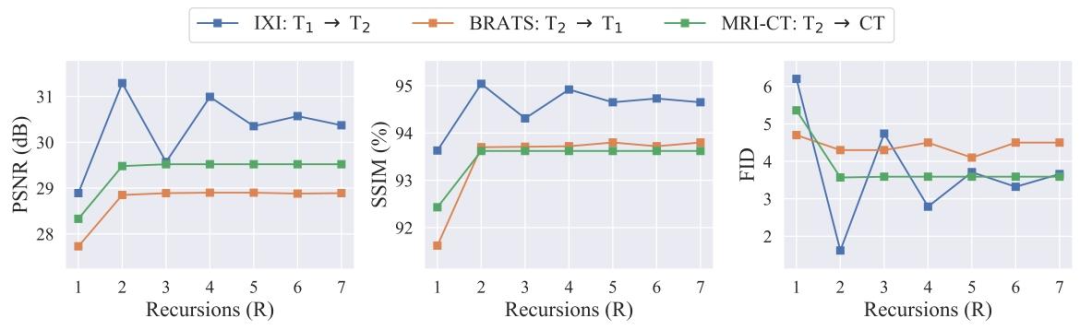
Fig. 8. Performance of SelfRDB variants that prescribe varying numbers of recursions to obtain target-image estimates in representative tasks. PSNR (left column), SSIM (middlecolumn) and FID (right column; 10× values shown for BRATS) are plotted as a function of 𝑅.

图8 在代表性任务中，通过设定不同递归次数以获取目标图像估计的SelfRDB变体性能。峰值信噪比（PSNR，左列）、结构相似性指数（SSIM，中列）和弗雷歇初始距离（FID，右列；BRATS数据集显示的是10倍数值）均以递归次数𝑅为自变量绘制。

Table

表

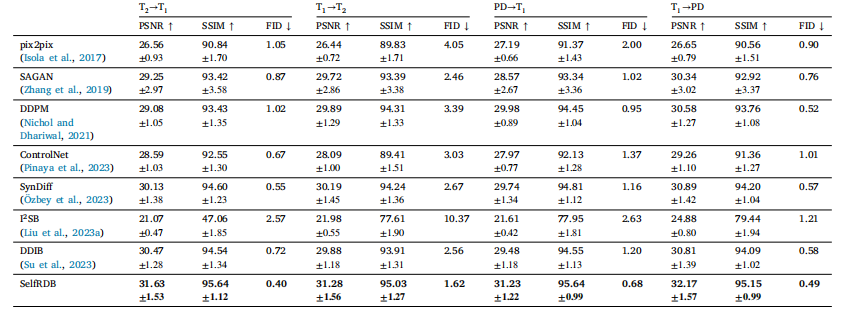
Table 1Multi-contrast MRI translation in IXI. PSNR (dB) and SSIM (%) are listed as mean ± std across the test set, along with FID. Boldface marks the top-performing model in eachtask

表1 IXI数据集上的多对比度MRI转换结果 表中列出了测试集上各方法的峰值信噪比（PSNR，单位：dB）、结构相似性指数（SSIM，单位：%）以及弗雷歇初始距离（FID），所有指标均以“均值±标准差”（mean ± std）形式呈现。其中，粗体标注的数值代表在对应转换任务中性能最优的模型。

Table 2Multi-contrast MRI translation in BRATS. PSNR (dB) and SSIM (%) are listed as mean ± std across the test set, along with FID

表2 BRATS数据集上的多对比度磁共振成像（MRI）转换结果 表中列出了测试集上的峰值信噪比（PSNR，单位：分贝，dB）、结构相似性指数（SSIM，单位：%），以及弗雷歇初始距离（FID），所有指标均以“均值±标准差”（mean ± std）的形式呈现。

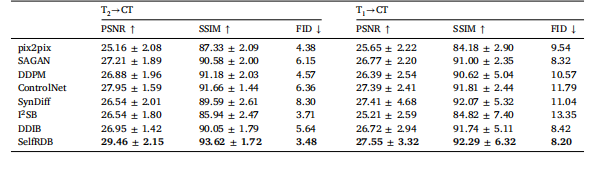
Table 3Multi-modal MRI-CT translation in the pelvic dataset. PSNR (dB) and SSIM (%) listed as mean ± std across the test set, alongwith FID.

表3 盆腔数据集上的多模态磁共振成像-计算机断层扫描（MRI-CT）转换结果 表中列出了测试集上的峰值信噪比（PSNR，单位：分贝，dB）、结构相似性指数（SSIM，单位：%），以及弗雷歇初始距离（FID），所有指标均以“均值±标准差”（mean ± std）的形式呈现。

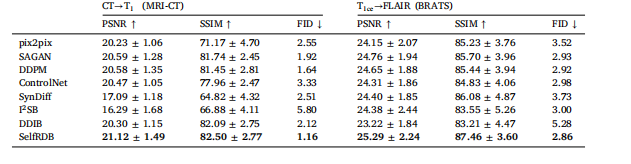
Table 4Challenging translation tasks. PSNR (dB) and SSIM (%) listed as mean ± std across the test set, along with FID.

表 4 挑战性转换任务（的评估结果）表中列出了测试集上的峰值信噪比（PSNR，单位：分贝，dB）、结构相似性指数（SSIM，单位：%），以及弗雷歇初始距离（FID），所有指标均以 “均值 ± 标准差”（mean ± std）的形式呈现

Table 5Average training times per cross-section (sec), inference times per cross-section (sec) and memory load (gigabytes).

表5 每一层横截面的平均训练时间（秒，sec）、每一层横截面的推理时间（秒，sec）以及内存占用（千兆字节，gigabytes）。

Table 6Performance of SelfRDB variants on representative medical image translation tasks. A variant ablated of a soft prior on the source modality, a variant ablated of self-consistenttarget-image estimates, a variant that received stationary guidance from the noise-added source image (𝒚𝜖 ) instead of the original source image (𝒚), and a variant that entirelyablated stationary source-image guidance were considered

表6 SelfRDB各变体在代表性医学图像转换任务上的性能 本表格对比了SelfRDB模型的四种变体性能，具体包括：去除源模态软先验的变体、去除自一致性目标图像估计的变体、使用添加噪声的源图像（𝒚𝜖）而非原始源图像（𝒚）提供固定引导的变体，以及完全去除固定源图像引导的变体。