目录

有回代跟无回代的主元消去法的比较

线性方程组的一般形式

有回代过程的主元消去法步骤

代码实现：

参考：《嵌入式系统软件设计中的常用算法》

有回代跟无回代的主元消去法的比较

有回代是用回代去替代无回代过程对主对角线上方的系数进行消元和计算行的其他系数的过程，有回代计算量减少，更适用于大矩阵的求解；

注：无回代过程的主元消去法在这个链接：

嵌入式算法：“无回代过程主元消去法”解线性方程组（含C代码）_KPer_Yang的博客-CSDN博客

线性方程组的一般形式

在多输入多输出系统中，假n*n的线性方程组的一般形式：

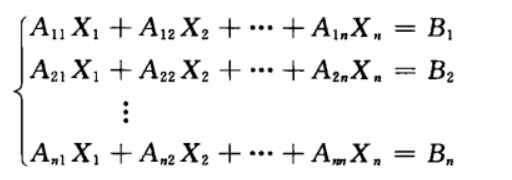
写成矩阵形式：

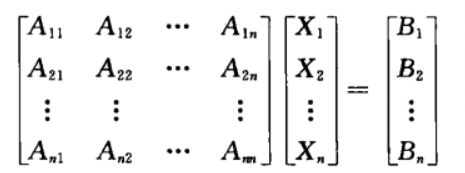
有回代过程的主元消去法步骤

'''
一般步骤：

1、按照左上角开始，按照对角线进行循环：

​	a、将列的绝对值最大的数作为主元，并且将该行调整到对角线上（提高精度）；

​	b、主元所在的行除以主元，使得主元=1；

​	c、进行高斯消元，将主元所在的列的下面行的数变为0（消元），这个过程按照下式对非主元的主元右边其他列的系数进行更新；

2、回代过程，自底向上回代；；
'''

代码实现：

#include<stdio.h>
#include<math.h>
#define N 3 	//方程组数
float A[N][N+1];//增广矩阵系数
float X[N]; 	//方程组的解

void findmain(int i) //寻找i列的主元，将其移到前当处理行位置
{
    int j,k;
    float c;
    c = fabs(A[i][i]); k=i;//初始化主元
    for(j=i+1; j<N; j++)   //向下寻找绝对值最大的行
    {
        if(fabs(A[j][i]>c)
        {
            c = fabs(A[j][i]);
            k = j;
        }
    }
    if(k!=i)
   	{
       	for(j = 0; j <= N; j++) //将主元所在行交换到当前处理行位置
   		{
        	c = A[k][j];
            A[k][j] = A[i][j];
            A[i][j] = c;
    	}
    }

}
           
void divmain(int i) //主元所在系数行除以主元，使得主元=1
{
	int j;
    float c;
    c = A[i][i];
    A[i][i] = 1.0;
    for(j = i+1; j < =N; j++) A[i][j] /= c;
}
           
void del(int i)//进行第i列的消元处理
{
    int j, k;
    float c;
    //这里体现和无回带的区别:无回代j=0；有会带j=i+1;也就是说回代过程从只需要将主元列下面的行变换成0；
    for(j=i+1; j < N; j++)
    {
        c = A[j][i];
        A[j][i] = 0;
        for(k = i+1; k < =N; k++) A[j][k] -= c*A[i][k];//调整同行的其他系数
    }
}
           
void nonbacksubstitution_elimination()
{
    //消元过程
    for(int i = 0; i < N; ++i) //i:行
    {
        if(i < N - 1) findmain(i);
        divmain(i);
        del(i);
    }
    //回代过程
    for(i = N-2; i >= 0; i--)//自底向上回代
    {
        for(j = N; j > i; i--) A[i][N] -= A[i][j]*A[j][N]; //自左向右求解
    }
    for(int i = 0; i < N; ++i) X[i] = A[i][N];//保存解
}