MNIST简单线性模型训练过程的原理
理解一下这个loss到底是什么,根据查阅相关资料和程序分析,这个loss应该是这个批次,即这64个十维向量输出的所有概率损失求平均或者求和得到的,根据球的的这个损失使用后续的优化算法找到使其梯度下降的最快的方向,这里这个梯度的求取是矩阵梯度的运算,这个在高等数学和线性代数中并没有深入了解过,但可以类比一下微积分里梯度的概念,只不过微积分是连续的函数,矩阵是离散的数据,这样的数据也是可以求取梯度的。
MNIST数据集包含四个文件,训练集图片数据,训练集标签数据,测试集图片数据,测试集标签数据。可以自己去官网上手动下载,也可以在数据集加载时自动进行下载。在这次训练中,我使用自动下载的方法。数据集文件如下图所示:
接下来进行数据加载操作:
import torchvision
from torchvision import transforms
train_ds=torchvision.datasets.MNIST(
'data/',
train=True,
transform=transforms.ToTensor(),
download=True
)
test_ds=torchvision.datasets.MNIST(
'data/',
train=False,
transform=transforms.ToTensor(), #转换,图片格式(c,h,w),像素取值范围归一化为0-1
download=True
)使用torchvision模块的datasets包里的MNIST数据集,设置根目录为data,训练集的train参数为True,由于pytorch的所有操作处理的都是张量格式的数据,把得到的图像数据集转换为张量格式,一个矩阵(channels,height,weight),MNIST数据集属于灰度图像,通道数为1,同时也是28*28大小的图像。
torchvision模块是pytorch框架下的一个重要模块,主要包括三个包,models包,transforms包
datasets包,models里存放了一些经典的神经网络,transform是一系列对图像增强的函数,比如图像的裁剪变换,旋转变换,数据标准化等,datasets包提供了一些经典数据集的加载函数。具体内容在官网上由详细的说明。
import torch
train_dl=torch.utils.data.DataLoader(train_ds,batch_size=64,shuffle=True)
test_dl=torch.utils.data.DataLoader(test_ds,batch_size=46)
print(len(train_dl.dataset))
print(len(train_dl))
print(len(test_dl.dataset))
print(len(test_dl))60000 938 10000 218
接下来进行图像的预处理操作,如上图,把读取进来的数据使用torch.utils.data模块下的DataLoader进行分批处理,这里设置的批次大小是64,训练集共有938批数据,测试集共218批数据。
from torch import nn
class Model(nn.Module):
def __init__(self):
super().__init__()
self.liner_1=nn.Linear(28*28,120)
self.liner_2=nn.Linear(120,84)
self.liner_3=nn.Linear(84,10)
def forward(self,input):
x=input.view(-1,28*28) #将输入展平为2维,28*28行,1列作为输入特征,
x=torch.relu(self.liner_1(x))
x=torch.relu(self.liner_2(x))
x=self.liner_3(x)
return x
定义一个模型,继承自nn.Module包,初始化父类__init__()方法,在__init__()中,是定义这个网络结构,三个线性结构,开始输入是一张图片上的28*28个像素值特征,这里设定输出为120个,即第一层神经网络传播向第二层时每张图片上的728个输入特征给以120组权重偏置参数,w1*x1+b1+w2*x2+b2+...+w784*x784+b784,经过这样一次传播得到一个输出神经元,这里设定了120个输出神经元,所以我的理解是共有120组这样的784对权重偏重参数,他们是不相同的,经过后续优化得到这样的120组每组的784对权重偏置参数,再经过后续的两次传播使用的是相同的原理,最后输出的一个这张图片的十维向量(也可以说是一维的含是个元素的向量,这个具体应该怎么表述还不清楚)刚好满足对应位置上的得分或者经过softmax转化成的最大概率和这张图像的真实labels的10维独热向量的1所在的位置是一致的,这样就可以认为预测正确,整个模型做的事情也就是最后优化后的参数使得这样的预测正确数量尽可能的高。
这里120,84都是自己设置的隐藏层神经元个数,最后输出的10要跟这个模型所具有的类别数一致,MNIST数据集是手写0到9的10个数字的数据集,共10个类别,最终输出应该是10,以便后续的比较和调优。
之后进入前向传播函数,传入的参数input是train_dl的一个批次的数据的张量数据,dataloader加载处理的数据在这个例子中是64对元组形式的数据,元组的第一个参数是图像的张量数据,第二个参数是这张图像对应的真实标签,这个真实标签是MNIST数据集提供的,读取数据时可以读取进来,这个在后面的模型训练中可以知道,对这个批次的64张图像可以依次处理,先展平成28*28行一列的数据,因这里使用的是线性模型,只能把模型展开进行,这对于入门来说也便于理解,之后的 卷积核对图像加权求和卷积核里的每个参数也是一个权重,类似于线性模型的扩展,这个以后讨论。
model=Model()
loss_fn=nn.CrossEntropyLoss() #初始化交叉熵损失函数
optimizer = torch.optim.SGD(model.parameters(),lr=0.001) #初始化优化器
这段代码开始实例化一下上述刚刚定义的模型,定义一个损失函数来评价损失,求取这个损失函数的梯度,进行参数优化,在分类问题中,使用最多的就是交叉熵损失函数,这个函数的大概含义就是把得到的十维输出向量和真实标签y的十维独热向量进行比较,求取一个批次的概率损失。这个后续模型处理中详细讨论。对于优化器来说,model.parameters()是nn.Module提供的直接获取需要更新的所有权重参数的方法,lr=0.001是一个学习率设置,学习率设置要合适,过小的话学习速率过慢,过大的话容易在极值点处震荡。更新方法w=w-lr*grad,这个容易理解,类比一次函数的斜率*步长。
device="cuda" if torch.cuda.is_available() else "cpu"
print("using {} device".format(device))
model=Model().to(device)这段代码是运行设备的选择,判断电脑是否有英伟达显卡,并把实例化的模型放到指定设备上,学习阶段cpu够用大部分模型,但在实际应用中cpu难以满足生产的需要,具体cuda环境怎么配置之后在讨论。
# 训练函数
def train(dl, model, loss_fn, optimizer):
size = len(dl.dataset) #当前数据集样本总数量
num_batches = len(dl) #当前dataloader总批次数
train_loss, correct = 0, 0
for x, y in dl:
x, y = x.to(device), y.to(device)
pred = model(x)
loss = loss_fn(pred, y)
optimizer.zero_grad()
loss.backward()
optimizer.step()
with torch.no_grad():
correct += (pred.argmax(1) == y).type(torch.float).sum().item()
train_loss += loss.item()
correct /= size
train_loss /= num_batches
return correct, train_loss这段代码定义了一个训练函数,传入参数需要有四个,dl是预处理后的数据,在这个例子中包含64张图片的张量以及每张图片对应的真实标签。model是实例化的模型,用于对输入张量进行神经网络操作得到预测的输出,loss_fn是传入的损失函数,这个模型选择的是在分类问题中最常用的交叉熵损失函数,optimizer是在训练过程中的优化器选择,这个模型选择的SGD优化器,即随机梯度下降算法,常用的几种优化器之后探讨。
开始先获取整个数据集的样本总数量和总批次数,便于后续计算正确率和损失率。下面进入循环,遍历批处理后的数据集,每次取出一批64个数据,这64个数据的张量x和其对应的真实标签y,循环体是对这64张图片进行的训练,即对这一个批次的图片进行的训练,这里要注意,这64组数据使用的是同一组权重参数,这么做的原因是使这一组权重参数训练不同的手写数字照片得到输出的十维向量都尽可能的能够正确拟合其真实的标签,在应用时不会因数字的不同而预测的准确率不一致。
进入循环把x,y都移入训练设备上,把输入张量x作为参数输入给之前定义的model,model返回一个十维向量,把这个返回值作为pred,这个十维向量不同位置上的数值表示对应类别的得分情况,数值越大,系统认为这个输入越有可能是这个类别。接下来就是计算损失,传入预测的十维向量和真实类别y的十维标签,这个标签在其对应真实类别位置值为1,其他位置是0,交叉熵损失函数的公式在其假类别上的0乘上预测结果,这样也是0,累加下来,只有预测的真实位置的概率才是有意义的,这里要注意,交叉熵损失函数内置了softmax()方法,能够把预测得分转换为概率,这个转换也有对应的公式,这里不详细展开。理解一下这个loss到底是什么,根据查阅相关资料和程序分析,这个loss应该是这个批次,即这64个十维向量输出的所有概率损失求平均或者求和得到的,根据球的的这个损失使用后续的优化算法找到使其梯度下降的最快的方向,这里这个梯度的求取是矩阵梯度的运算,这个在高等数学和线性代数中并没有深入了解过,但可以类比一下微积分里梯度的概念,只不过微积分是连续的函数,矩阵是离散的数据,这样的数据也是可以求取梯度的。这样可以根据梯度方向先前的系统随机生成的参数,以及优化器里设置的学习率使用学习率函数进行参数的更新优化。后面几行合起来进行理解,loss是一个批次的总的损失,是对这个批次的所有64个输出和真实类别进行交叉熵求出损失再求和或求平均得到的结果,optimizer.zero_grad()是梯度清零,怎么理解,目的是确保每个训练迭代都已新的梯度开始计算,放在调用loss.backward()之前,loss是整个神经网络的这一组的所有参数得到的损失值,使用反向传播函数找到下降最快的方向进行参数更新,这个方向可以使得损失函数朝这个方向的损失下降最快,optimizer.step()进行参数更新,这里有一个学习率的设置问题要注意一下。
下面提取出for循环里的如下代码:
with torch.no_grad():
correct += (pred.argmax(1) == y).type(torch.float).sum().item()
train_loss += loss.item()
with torch.no_grad(): 这行代码是一个上下文管理器,可以暂时关闭自动求导功能,一个correct是一个批次预测正确的个数,pred.argmax(1)==y是获取预测结果中每个样本的最大概率对应的类别索引与y一致,则预测正确,这个正确是一个布尔张量,.type(float)转换为浮点张量,.sum进行对一个批次中的预测正确的样本个数累加,.item()将浮点张量转换为一个标量数据。再接下来的训练中,50个epoch,每个epoch里调用一次train函数,一个train训练一遍数据集,train里for循环采用分批训练,这个上下文管理器的内容就是运行一次统计64个样本的预测正确数量,统计这一批次的损失,循环完所有批次就是统计60000个训练样本里的所有预测正确个数,统计938个批次总的损失,跳出批次训练循环后,correct除以size总样本数60000得到预测正确率,用来评估这组参数的预测情况,同样使用所有批次的损失和train_loss除以总的批次数,得到平均批次损失值,并把这两个数据作为函数返回值。
# 测试函数
def test(test_dl, model, loss_fn):
size = len(test_dl.dataset)
num_batches = len(test_dl)
test_loss, correct = 0, 0
with torch.no_grad():
for x, y in test_dl:
x, y = x.to(device), y.to(device)
pred = model(x)
loss = loss_fn(pred, y)
test_loss += loss.item()
correct += (pred.argmax(1) == y).type(torch.float).sum().item()
correct /= size
test_loss /= num_batches
return correct, test_loss这是测试函数的代码,用于使用刚刚在训练集上得到的参数输入测试集进行测试其效果,这里我的理解是测试集和训练集的数据格式是完全一致的,只是样本数量不一样,很容易理解,测试时候并不需要使用那么多的样本进行测试。这里的整体逻辑和train函数是一样的,只不过不用进行反向传播和梯度更新,只需求出正确率和损失即可,用来评价效果。
epochs = 50
train_loss = []
train_acc = []
test_loss = []
test_acc = []
for epoch in range(epochs):
epoch_acc, epoch_loss = train(train_dl, model, loss_fn, opt)
epoch_test_acc, epoch_test_loss = test(test_dl, model, loss_fn)
train_acc.append(epoch_acc)
train_loss.append(epoch_loss)
test_acc.append(epoch_test_acc)
test_loss.append(epoch_test_loss)
template = ("epoch:{:2d}, train_Loss:{:.5f}, train_acc:{:.1f},test_Loss:{:.5f}, test_acc:{:.1f}")
print(template.format(epoch, epoch_loss, epoch_acc*100, epoch_test_loss, epoch_test_acc*100))
print('Done')接下来就是训练五十个epoch,每个epoch是对数据集训练一遍,把每个epoch的train(),test()返回的整个训练集的训练正确率,训练平均损失,测试正确率,测试平均损失加入到相关列表中,并每经历一个epoch打印输出一次,用来查看训练效果。训练情况如下:

之后对以上统计结果进行可视化:
损失预测可视化:
import matplotlib.pyplot as plt
plt.plot(range(epochs), train_loss, label='train_loss')
plt.plot(range(epochs), test_loss, label='test_loss')
plt.legend()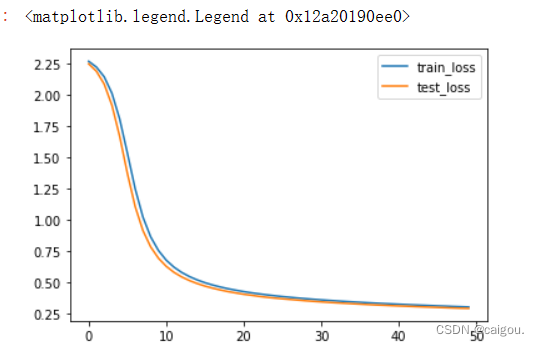
正确率预测可视化:
plt.plot(range(epochs), train_acc, label='train_acc')
plt.plot(range(epochs), test_acc, label='test_acc')
plt.legend()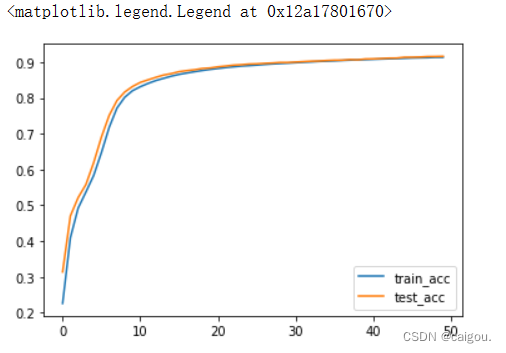
更多推荐
 已为社区贡献2条内容
已为社区贡献2条内容







所有评论(0)