一、特征值和特征向量

1 特征值与特征向量的定义

Ax=λx
设 A 是 n 阶方阵，如果数值λ和 n 维非零列向量 x 使关系式 Ax=λx 成立(即只伸缩不旋转)，
那么这样的数λ称为矩阵 A 的“特征值”。

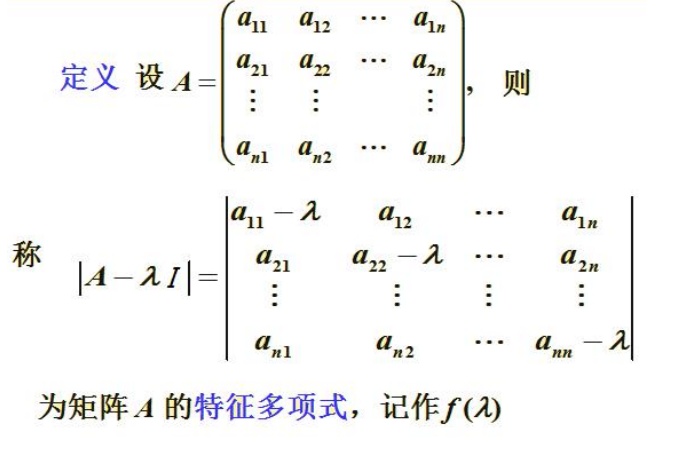
计算得到特征值和特征向量的意义？特征值与特征向量表达了一个线性变换的特征，特征向量
将一个矩阵进行正交分解，判断出在哪些方向只拉伸不扭曲来简化计算量，得到了特征值与特征向量就是得到了某个矩阵导致的伸缩比例和伸缩方向，其目的主要用于降维

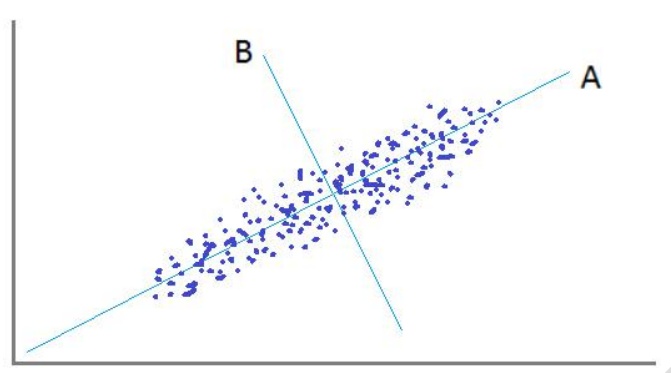
上图通过分析特征值与特征向量就可以将二维数据变成一维数据分析。

2 opencv 接口计算特征值与特征向量

bool eigen(InputArray src, OutputArray eigenvalues, OutputArray eigenvectors = noArray()); 功能：获取特征值和特征向量 参数：
src：原图或者数据
eigenvalues：特征值
eigenvectors：特征向量

案例：

#include <opencv2/opencv.hpp> 
#include <iostream> 
using namespace std; 
using namespace cv; 
int main(int argc, char const *argv[]) 
{ 
	Mat data = (Mat_<double>(2, 2) << 1, 2, 2, 1); 
	Mat eigen_values, eigen_vector;
	 eigen(data, eigen_values, eigen_vector); 
	 for(int i = 0; i < eigen_values.rows; i++)
	 	{ 
	 		printf("eigen value %d: %.3fn", i, eigen_values.at<double>(i)); 
	 	}
 	cout << "eigen vector: " << endl << eigen_vector << endl; 
 	waitKey(0); 
 	return 0; 
}

执行结果:

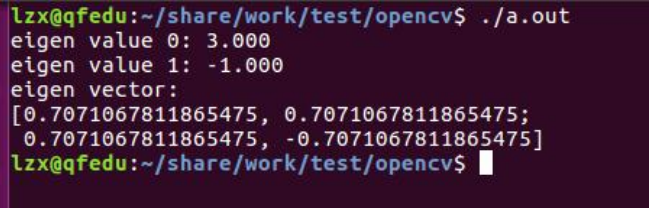
可以将矩阵扩大两倍看看，得到的特征值与特征向量如何变化。

建议：该系列教程可参照本人视频对应观看！

13_特征值与特征向量概念

14_特征值与特征向量opencv计算接口